强碰撞磁化尘埃等离子体中的漂移波

杨建荣; 毛杰键; 吴奇成; 刘萍; 黄立

doi:10.7498/aps.69.20200468

摘要

研究磁化尘埃等离子体的波动机理, 对相关实验、工业加工、天体空间探测等具有重要的价值. 本文研究了非均匀磁化尘埃等离子体系统的线性和非线性波动特性. 对处于均匀外磁场中的非均匀尘埃等离子体系统, 存在密度和温度梯度的非均匀环境, 考虑尘埃和中性粒子的强碰撞作用, 得到了一个二维非线性磁流体动力学方程. 通过线性化得到了色散关系, 系统既有强碰撞引起的阻尼波, 又有粒子漂移产生的谐波; 典型的数值参量分析结果表明, 量子参量修改了系统的尺度; 实频与漂移频率成正比关系, 而虚频与尘埃和中子间的碰撞频率有着比较复杂的关系, 粒子的碰撞引起了系统的耗散效应. 通过函数变换法, 获得了漂移的冲击波和爆炸波的解析解. 详细讨论了静电势随着主要物理量的变化, 研究结果显示, 静电冲击波的幅度和爆炸波的宽度都随尘埃密度和外界磁场强度的增大而增大, 随着碰撞频率的增大而减小, 随漂移速度而变化. 当时空相位较小时, 静电势变化很快, 一旦足够大时, 静电势将趋于稳定值, 最终达到稳定的状态. 最后对系统的稳定性问题进行了分析, 发现尘埃电荷量、量子参量、漂移速度都出现在扰动解中. 本文所得结果表明, 强碰撞效应、量子效应、粒子漂移和外界磁场等主要物理量都对尘埃漂移波的产生、演化和稳定性产生了重要的作用.

关键词:

Abstract

The study about the wave mechanism of magnetized dusty plasmas has important value to related experiment, industrial processing and exploring celestial space. The linear and nonlinear fluctuation characteristics of the nonuniform magnetized dust plasma system are researched in this paper. For the homogeneous external magnetic field and the nonuniform environment with density and temperature gradients, a two-dimensional nonlinear dynamic magnetoplasma equation is derived considering the strong impact between dust and neutral particles. The linear dispersion relation is obtained by the linearized method. There are both the damping wave causing by strong collision and the harmonic wave by particle drift. Employing the typical numerical parameters for analysis, the results display that the quantum parameter modifies the system lengths; the real wave frequency is proportion to the drift frequency; the imaginary wave frequency has complex relationship with the collision frequency between dust and neutrals, and the collision of particles causes the dissipation effects to the system. Besides, the analytical solutions of drift shock wave and explosive wave are solved by function change method. The variation about the electrostatic potential with the main physical parameters is discussed in detail. It is shown that the strength of the electrostatic shock wave and the width of the explosive wave increase with increasing the dust density and magnetic field intensity, decrease with increasing the collision frequency, change with the drift velocity. When the space-time phase is small, the electrostatic potential changes quickly; once big enough, the potential tends to be stable value and reaches stable state eventually. Finally, the stability of the system is discussed. It is found that the dusty charge, quantum parameter, drift velocity all appear in the disturbed solution. All these results in the paper show that the strong collision effect, quantum effect, particle drift and magnetic field all play important role to the generation, evolution and stability of drift waves.

Keywords:

作者及机构信息

1.
上饶师范学院物理与电子信息学院, 上饶　334001

2.
江西省电动汽车部件智能化工程技术研究中心, 上饶　334001

3.
电子科技大学中山学院电子信息学院, 中山　528402

通信作者: 杨建荣, sryangjr@163.com ; 毛杰键, maojj2006@163.com ;

Authors and contacts

1.
School of Physics and Electronics, Shangrao Normal University, Shangrao 334001, China

2.
Engineering Technology Research Center of Intelligent Electric Vehicle Components of Jiangxi Province, Shangrao 334001, China

3.
College of Electron and Information Engineering, University of Electronic Science and Technology of China Zhongshan Institute, Zhongshan 528402, China

Corresponding author: Yang Jian-Rong, sryangjr@163.com ; Mao Jie-Jian, maojj2006@163.com ;

文章全文 : translate this paragraph

参考文献

[1]	Morfill G E, Ivlev A V 2009 Rev. Mod. Phys. 81 1353 Google Scholar
[2]	马锦秀 2006 物理 35 244 Ma J X 2006 Physics 35 244
[3]	Merlino R L, Goree J 2004 Phys. Today 57 32
[4]	Shukla P K, Mamun A A 2002 Introduction to Dusty Physics Plasmas (Bristol: Institute of Physics) pp29−35
[5]	Verheest F 2000 Waves in Dusty Space Plasmas (Dordrecht: Kluwer Academic Publishers, The Netherlands) pp11−56
[6]	Shukla P K 2002 Dust Plasma Interaction in Space (New York: Nova Science) pp156−159
[7]	Liang Z F, Tang X Y 2013 Commun. Nonlinear Sci. Numer. Simul. 18 3014 Google Scholar
[8]	Barkan A, Merlino R L, Angelo N D 1995 Phys. Plasmas 2 3563 Google Scholar
[9]	Merlino R L 2014 J. Plasma Phys. 80 773 Google Scholar
[10]	Rao N N, Shukla P K, Yu M Y 1990 Planet. Space Sci. 18 543
[11]	Shukla P K, Rahman H U 1996 Phys. Plasmas 3 430 Google Scholar
[12]	Haas F 2005 Phys. Plasmas 12 062117 Google Scholar
[13]	Haque Q, Mahmood S 2008 Phys. Plasmas 15 034501 Google Scholar
[14]	Masood W 2009 Phys. Lett. A 373 1455 Google Scholar
[15]	Masood W, Karim S, Shah H A, Siddiq M 2009 Phys. Plasmas 16 042108 Google Scholar
[16]	Yang J R, Lv K, Xu L, Mao J J, Liu X Z, Liu P 2017 Chin. Phys. B 26 065200
[17]	Yang J R, Wu B, Mao J J, Liu P, Wang J Y 2014 Commun. Theor. Phys 62 871
[18]	Moslem W M, Shukla P K, Ali S, Schlickeiser R 2007 Phys. Plasmas 14 042107 Google Scholar
[19]	Sadiq M, Ali S, Sabry R 2009 Phys. Plasmas 16 013706 Google Scholar
[20]	Sharma P, Patidar A, Jain S, Vyas B 2018 Phys. Plasmas 25 083714 Google Scholar
[21]	Jorge R, Ricci P, Loureiro N F 2018 Phys. Rev. Lett. 121 165001 Google Scholar
[22]	Kumar A, Das A, Kaw P 2019 Phys. Plasmas 26 8
[23]	Mehdipoor M 2020 The Eur. Phys. J. Plus 135 299 Google Scholar
[24]	Masood W, Karim S, Shah H A 2010 Phys. Scr. 82 045503 Google Scholar
[25]	Kato S 1968 Astrophys. Space Sci. 2 37 Google Scholar
[26]	Dev A N, Deka M K, Sarma J, Adhikary N C 2015 J. Korean Phys. Soc. 67 339 Google Scholar
[27]	Khan S A, Mushtaq A, Masood W 2008 Phys. Plasmas 15 013701 Google Scholar
[28]	Smith B A, Soderblom L, Beebe R, et al. 1981 Science 212 163 Google Scholar
[29]	Smith B A, Soderblom L, Batson R, et al. 1982 Science 215 504 Google Scholar
[30]	Humes D H 1980 J. Geophys. Res. 85 5841 Google Scholar
[31]	Yang J R, Xu T, Mao J J, Liu P, Liu X Z 2017 Chin. Phys. B 26 015202 Google Scholar

施引文献

图 1 (14) 式实色散频率随着波数k和漂移速度v的变化, $\theta = {{\text{π}}}/{3}$, 对应的其他参量见(11)式

Fig. 1. Variation of the real dispersion frequency with the wave number k and drift velocity v determined by Eq. (14) for $\theta = {{\text{π}}}/{3}$. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 2 (14)式实色散频率随着波数k和倾斜角$ \theta $的变化, 对应的参量见(11)式

Fig. 2. Variation of the real dispersion frequency with the wave number k and obliqueness angle $ \theta $ determined by Eq. (14), and the parameters given in Eq. (11).

下载: 全尺寸图片幻灯片

图 3 (14)式实色散频率随着波数k和尘埃密度$n_{\rm d}$的变化, $\theta = {{\text{π}}}/{3}$, 对应的其他参量见(11)式

Fig. 3. Variation of the real dispersion frequency with the wave number k and the dust density $n_{\rm d}$ determined by Eq. (14) for $\theta = {{\text{π}}}/{3}$. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 4 (14)式实色散频率随着波数k和磁场强度$ B_0 $的变化, $\theta = {{\text{π}}}/{3}$, 对应的其他参量见(11)式

Fig. 4. Variation of the real dispersion frequency with the wave number k and magnetic field $ B_0 $ determined by Eq. (14) for $\theta = {{\text{π}}}/{3}$. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

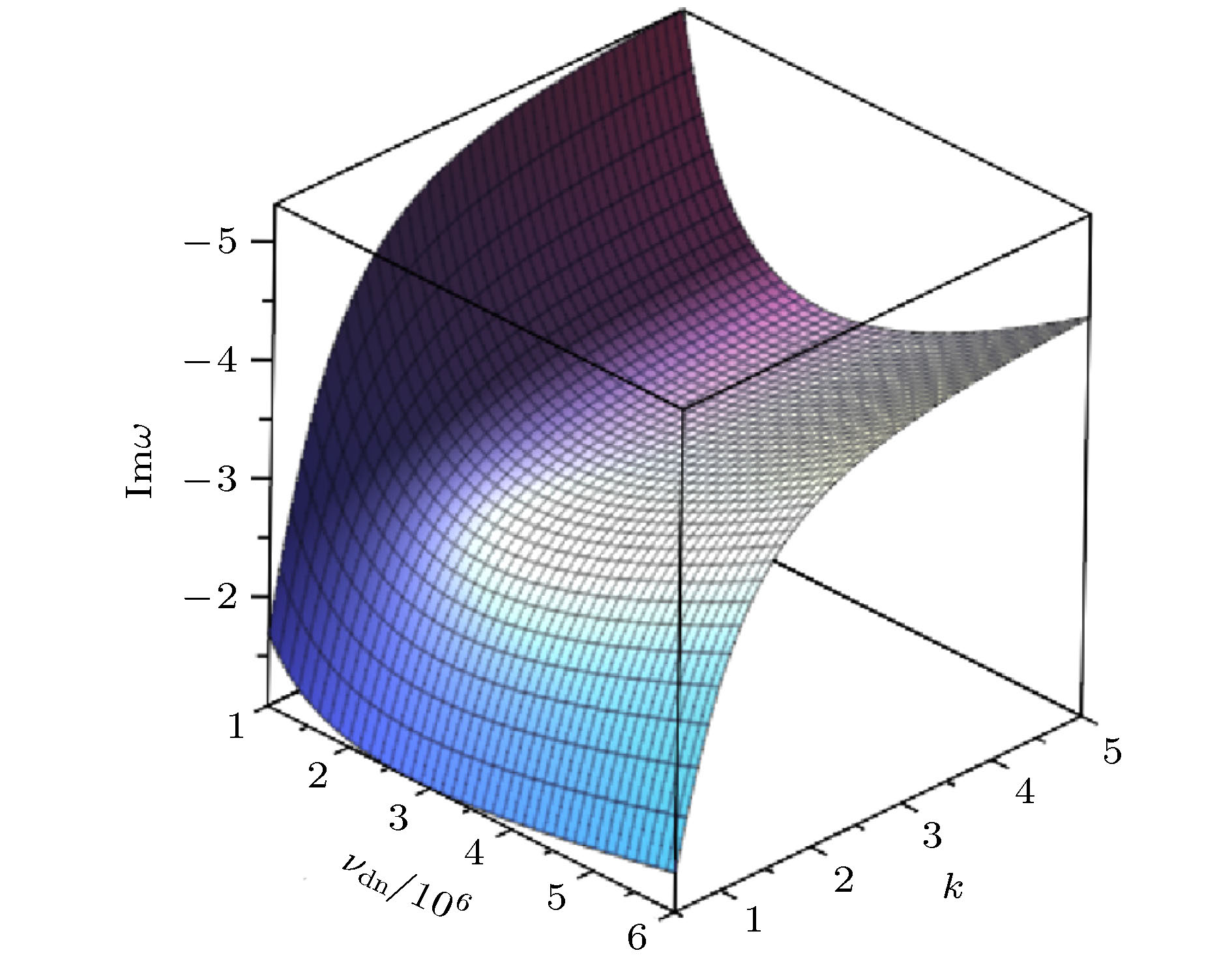
图 5 (15)式虚色散频率随着波数k和碰撞频率$ \nu_{\rm {dn}} $的变化, $\theta = {{\text{π}}}/{3}$, 对应的其他参量见(11)式

Fig. 5. Variation of the imaginary dispersion frequency with the wave number k and the collision frequency $ \nu_{\rm {dn}} $ determined by Eq. (15) for $\theta = {{\text{π}}}/{3}$. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 6 (18)式冲击波$ \varPhi_1 $随着尘埃密度$ n_{\rm d} $的变化. 对应的参量为$ k_{2} = 10 $, $ k_{3} = 1 $, 其他参量见(11)式

Fig. 6. Variation of the shock wave $ \varPhi_1 $ with the dust density $ n_{\rm d} $ by Eq.(18) for $ k_{2} = 10 $, $ k_{3} = 1 $. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 7 (18)式冲击波$ \varPhi_1 $随着碰撞频率$ \nu_{\rm {dn}} $的变化. 对应的参量为$ k_{2} = 10 $, $ k_{3} = 2 $, 其他参量见(11)式

Fig. 7. Variation of the shock wave $ \varPhi_1 $ with the collision frequency $ \nu_{\rm {dn}} $ by Eq.(18) for $ k_{2} = 10 $, $ k_{3} = 2 $. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 8 (18)式冲击波$ \varPhi_1 $随着漂移速度v的变化. 对应的参量为$ k_{2} = 5 $, $ k_{3} = 2 $, 其他参量见(11)式

Fig. 8. Variation of the shock wave $ \varPhi_1 $ with the drift velocity v by Eq.(18) for $ k_{2} = 5 $, $ k_{3} = 2 $. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 9 (18)式冲击波$ \varPhi_1 $随着磁场强度$ B_0 $的变化. 对应的参量为$ k_{2} = 10 $, $ k_{3} = 1 $, 其他参量见(11)式

Fig. 9. Variation of the shock wave $ \varPhi_1 $ with the magnetic field $ B_0 $ by Eq.(18) for $ k_{2} = 10 $, $ k_{3} = 1 $. Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 10 (19)式爆炸波$ \varPhi_2 $随着尘埃密度$ n_{\rm d} $的变化. 对应的参量为$ k_{2} = 2 $, $ k_{3} = 1 $, $ n_{\rm d} = 1.2\times10^{18}{\ \rm{cm}^{-3}} $ (实线), $ n_{\rm d} = 1.4\times10^{18}{\ \rm{cm}^{-3}} $(虚线), 其他参量见(11)式

Fig. 10. Profile of the explosive wave $ \varPhi_2 $ by Eq. (19) with $ k_{2} = 2 $, $ k_{3} = 1 $, $ n_{\rm d} = 1.2\times10^{18}{\ \rm{cm}^{-3}} $ (solid line), and $ n_{\rm d} = 1.4\times10^{18}{\ \rm{cm}^{-3}} $ (dash line). Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

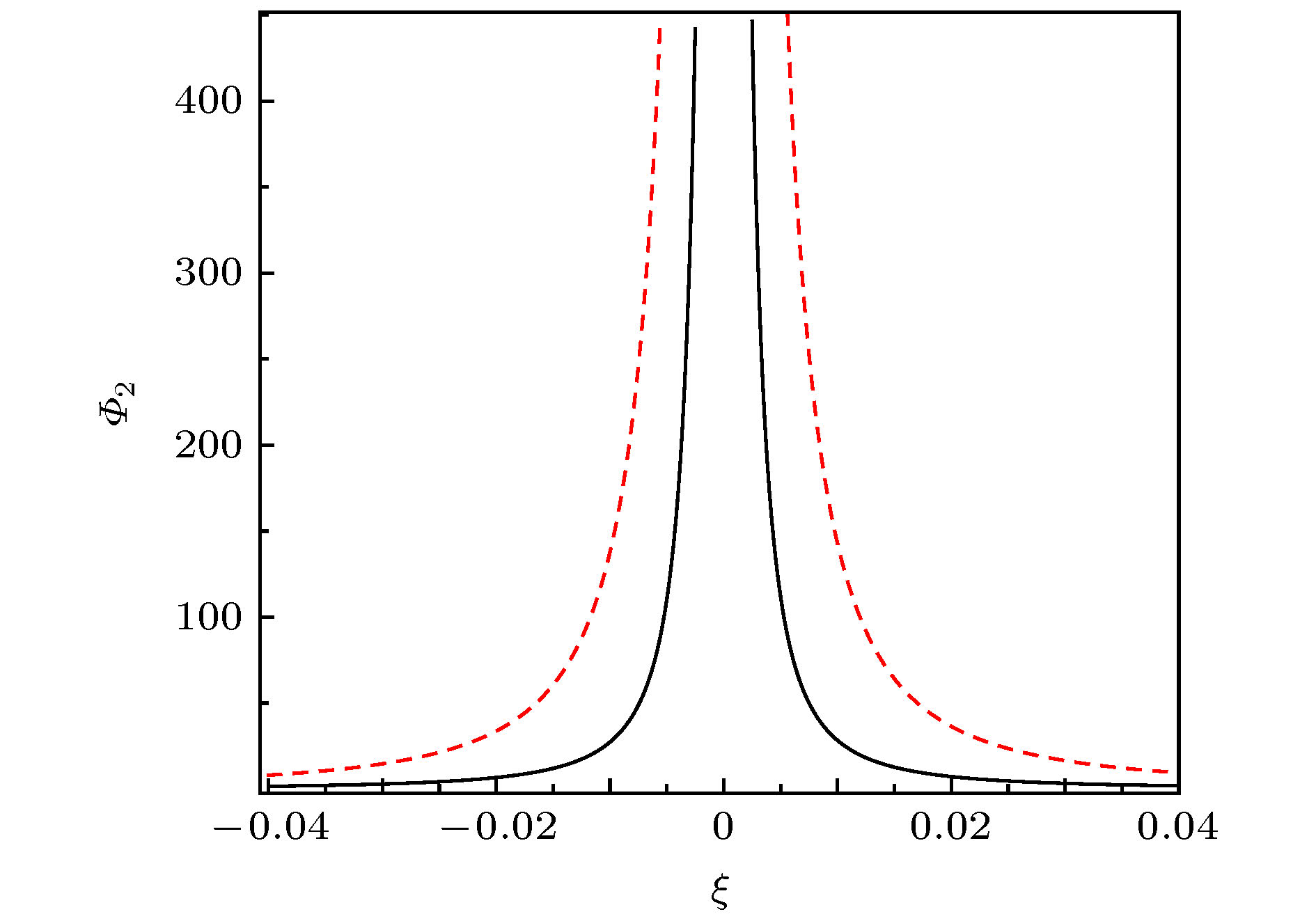
图 11 (19)式爆炸波$ \varPhi_2 $随着碰撞频率$ \nu_{\rm {dn}} $的变化. 对应的参量为$ k_{2} = 2 $, $ k_{3} = 1 $, $ \nu_{\rm {dn}} = 10^{6}\ \rm{Hz} $(实线), $ \nu_{\rm {dn}} = 3\times 10^{6}\ \rm{Hz} $(虚线), 其他参量见(11)式

Fig. 11. Profile of the explosive wave $ \varPhi_2 $ given by Eq. (19) with $ k_{2} = 2 $, $ k_{3} = 1 $, $ \nu_{\rm {dn}} = 10^{6}\ \rm{Hz} $ (solid line), and $ \nu_{\rm {dn}} = 3\times10^{6}\ \rm{Hz} $ (dash line). Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 12 (19)式爆炸波$ \varPhi_2 $随着漂移速度v的变化. 对应的参量为$ k_{2} = 2 $, $ k_{3} = 1 $, $ v = 10^{3}\ \rm{cm/s} $ (实线), $ v = 10^{4}\ \rm{cm/s} $(虚线), 其他参量见(11)式

Fig. 12. Profile of the explosive wave $ \varPhi_2 $ given by Eq. (19) with $ k_{2} = 2 $, $ k_{3} = 1 $, $ v = 10^{3}\ \rm{cm/s} $ (solid line), and $ v = 10^{4}\ \rm{cm/s} $ (dash line). Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

图 13 (19)式爆炸波$ \varPhi_2 $随着磁场强度$ B_0 $的变化. 对应的参量为$ k_{2} = 2 $, $ k_{3} = 1 $, $ B_0 = 10^{8}\ \rm{G} $(实线), 和$ B_0 = 3\times 10^{8}\ \rm{G} $(虚线), 其他参量见(11)式

Fig. 13. Profile of the explosive wave $ \varPhi_2 $ given by Eq. (19) with $ k_{2} = 2 $, $ k_{3} = 1 $, $ B_0 = 10^{8}\ \rm{G} $ (solid line), and $ B_0 = 3\times10^{8}\ \rm{G} $ (dash line). Other parameters are given in Eq. (11).

下载: 全尺寸图片幻灯片

map

[1]	Morfill G E, Ivlev A V 2009 Rev. Mod. Phys. 81 1353 Google Scholar
[2]	马锦秀 2006 物理 35 244 Ma J X 2006 Physics 35 244
[3]	Merlino R L, Goree J 2004 Phys. Today 57 32
[4]	Shukla P K, Mamun A A 2002 Introduction to Dusty Physics Plasmas (Bristol: Institute of Physics) pp29−35
[5]	Verheest F 2000 Waves in Dusty Space Plasmas (Dordrecht: Kluwer Academic Publishers, The Netherlands) pp11−56
[6]	Shukla P K 2002 Dust Plasma Interaction in Space (New York: Nova Science) pp156−159
[7]	Liang Z F, Tang X Y 2013 Commun. Nonlinear Sci. Numer. Simul. 18 3014 Google Scholar
[8]	Barkan A, Merlino R L, Angelo N D 1995 Phys. Plasmas 2 3563 Google Scholar
[9]	Merlino R L 2014 J. Plasma Phys. 80 773 Google Scholar
[10]	Rao N N, Shukla P K, Yu M Y 1990 Planet. Space Sci. 18 543
[11]	Shukla P K, Rahman H U 1996 Phys. Plasmas 3 430 Google Scholar
[12]	Haas F 2005 Phys. Plasmas 12 062117 Google Scholar
[13]	Haque Q, Mahmood S 2008 Phys. Plasmas 15 034501 Google Scholar
[14]	Masood W 2009 Phys. Lett. A 373 1455 Google Scholar
[15]	Masood W, Karim S, Shah H A, Siddiq M 2009 Phys. Plasmas 16 042108 Google Scholar
[16]	Yang J R, Lv K, Xu L, Mao J J, Liu X Z, Liu P 2017 Chin. Phys. B 26 065200
[17]	Yang J R, Wu B, Mao J J, Liu P, Wang J Y 2014 Commun. Theor. Phys 62 871
[18]	Moslem W M, Shukla P K, Ali S, Schlickeiser R 2007 Phys. Plasmas 14 042107 Google Scholar
[19]	Sadiq M, Ali S, Sabry R 2009 Phys. Plasmas 16 013706 Google Scholar
[20]	Sharma P, Patidar A, Jain S, Vyas B 2018 Phys. Plasmas 25 083714 Google Scholar
[21]	Jorge R, Ricci P, Loureiro N F 2018 Phys. Rev. Lett. 121 165001 Google Scholar
[22]	Kumar A, Das A, Kaw P 2019 Phys. Plasmas 26 8
[23]	Mehdipoor M 2020 The Eur. Phys. J. Plus 135 299 Google Scholar
[24]	Masood W, Karim S, Shah H A 2010 Phys. Scr. 82 045503 Google Scholar
[25]	Kato S 1968 Astrophys. Space Sci. 2 37 Google Scholar
[26]	Dev A N, Deka M K, Sarma J, Adhikary N C 2015 J. Korean Phys. Soc. 67 339 Google Scholar
[27]	Khan S A, Mushtaq A, Masood W 2008 Phys. Plasmas 15 013701 Google Scholar
[28]	Smith B A, Soderblom L, Beebe R, et al. 1981 Science 212 163 Google Scholar
[29]	Smith B A, Soderblom L, Batson R, et al. 1982 Science 215 504 Google Scholar
[30]	Humes D H 1980 J. Geophys. Res. 85 5841 Google Scholar
[31]	Yang J R, Xu T, Mao J J, Liu P, Liu X Z 2017 Chin. Phys. B 26 015202 Google Scholar

[1]	魏广宇, 陈凝飞, 仇志勇. 高能量粒子测地声模与Dimits区漂移波相互作用. , 2022, 71(1): 015201. doi: 10.7498/aps.71.20211430
[2]	苏瑞霞, 黄霞, 郑志刚. 耦合Frenkel-Kontorova双链的格波解及其色散关系. , 2022, 71(15): 154401. doi: 10.7498/aps.71.20212362
[3]	魏广宇, 陈凝飞, 仇志勇. 高能量粒子测地声模与Dimits区漂移波相互作用. , 2021, (): . doi: 10.7498/aps.70.20211430
[4]	李文秋, 赵斌, 王刚, 相东. 螺旋波等离子体中螺旋波与Trivelpiece-Gould波模式耦合及线性能量沉积特性参量分析. , 2020, 69(11): 115201. doi: 10.7498/aps.69.20200062
[5]	李文秋, 赵斌, 王刚. 电子温度对螺旋波等离子体中电磁模式能量沉积特性的影响. , 2020, 69(21): 215201. doi: 10.7498/aps.69.20201018
[6]	孙俊超, 张宗国, 董焕河, 杨红卫. 尘埃等离子体中的分数阶模型及其Lump解. , 2019, 68(21): 210201. doi: 10.7498/aps.68.20191045
[7]	杨雪, 丁大军, 胡湛, 赵国明. 中性和阳离子丁酮团簇的结构及稳定性的理论研究. , 2018, 67(3): 033601. doi: 10.7498/aps.67.20171862
[8]	徐彬, 李辉, 王占阁, 许正文, 吴健. 高密度尘埃等离子体的非相干散射理论研究. , 2017, 66(4): 049401. doi: 10.7498/aps.66.049401
[9]	陈海军, 张耀文. 空间调制作用下Bessel型光晶格中物质波孤立子的稳定性. , 2014, 63(22): 220303. doi: 10.7498/aps.63.220303
[10]	陈海军, 李向富. 二维线性与非线性光晶格中物质波孤立子的稳定性. , 2013, 62(7): 070302. doi: 10.7498/aps.62.070302
[11]	张娟, 周志刚, 石玉仁, 杨红娟, 段文山. 修正KP方程及其孤波解的稳定性. , 2012, 61(13): 130401. doi: 10.7498/aps.61.130401
[12]	刘三秋, 国洪梅. 极端相对论快电子分布等离子体中横振荡色散关系. , 2011, 60(5): 055203. doi: 10.7498/aps.60.055203
[13]	刘炳灿, 逯志欣, 于丽. 金属和Kerr非线性介质界面上表面等离子体激元的色散关系. , 2010, 59(2): 1180-1184. doi: 10.7498/aps.59.1180
[14]	仲生仁. 尘埃等离子体中非线性波的叠加效应及稳定性问题. , 2010, 59(4): 2178-2181. doi: 10.7498/aps.59.2178
[15]	季沛勇, 鲁楠, 祝俊. 量子等离子体中波的色散关系以及朗道阻尼. , 2009, 58(11): 7473-7478. doi: 10.7498/aps.58.7473
[16]	赵国伟, 徐跃民, 陈诚. 等离子体天线色散关系和辐射场数值计算. , 2007, 56(9): 5298-5303. doi: 10.7498/aps.56.5298
[17]	杨建宋, 李宝兴. 砷化镓离子团簇的稳定性研究. , 2006, 55(12): 6562-6569. doi: 10.7498/aps.55.6562
[18]	石雁祥, 葛德彪, 吴健. 尘埃粒子充放电过程对尘埃等离子体电导率的影响. , 2006, 55(10): 5318-5324. doi: 10.7498/aps.55.5318
[19]	周国成, 曹晋滨, 王德驹, 蔡春林. 无碰撞等离子体电流片中的低频波. , 2004, 53(8): 2644-2653. doi: 10.7498/aps.53.2644
[20]	洪学仁, 段文山, 孙建安, 石玉仁, 吕克璞. 非均匀尘埃等离子体中孤子的传播. , 2003, 52(11): 2671-2677. doi: 10.7498/aps.52.2671

计量

文章访问数: 5908
PDF下载量: 63
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

强碰撞磁化尘埃等离子体中的漂移波