Physics-informed neural networks based on source term decoupled and its application in discharge plasma simulation

Fang Ze; Pan Yong-Quan; Dai Dong; Zhang Jun-Bo

doi:10.7498/aps.73.20240343

Abstract

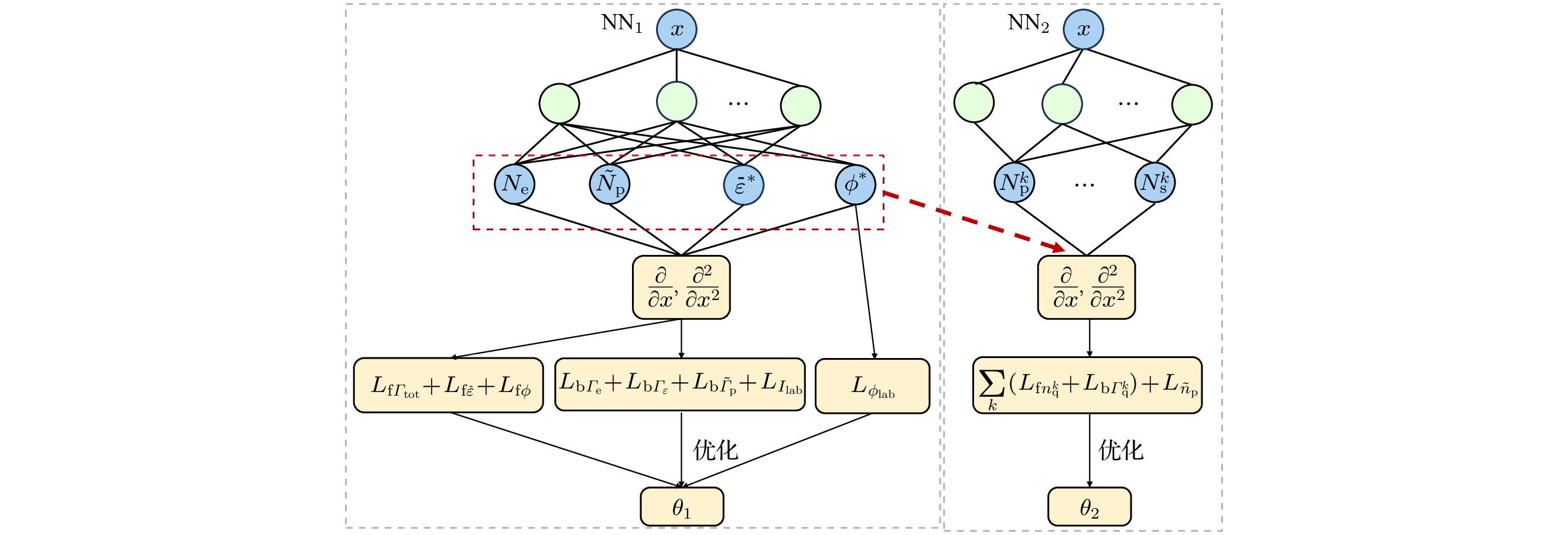
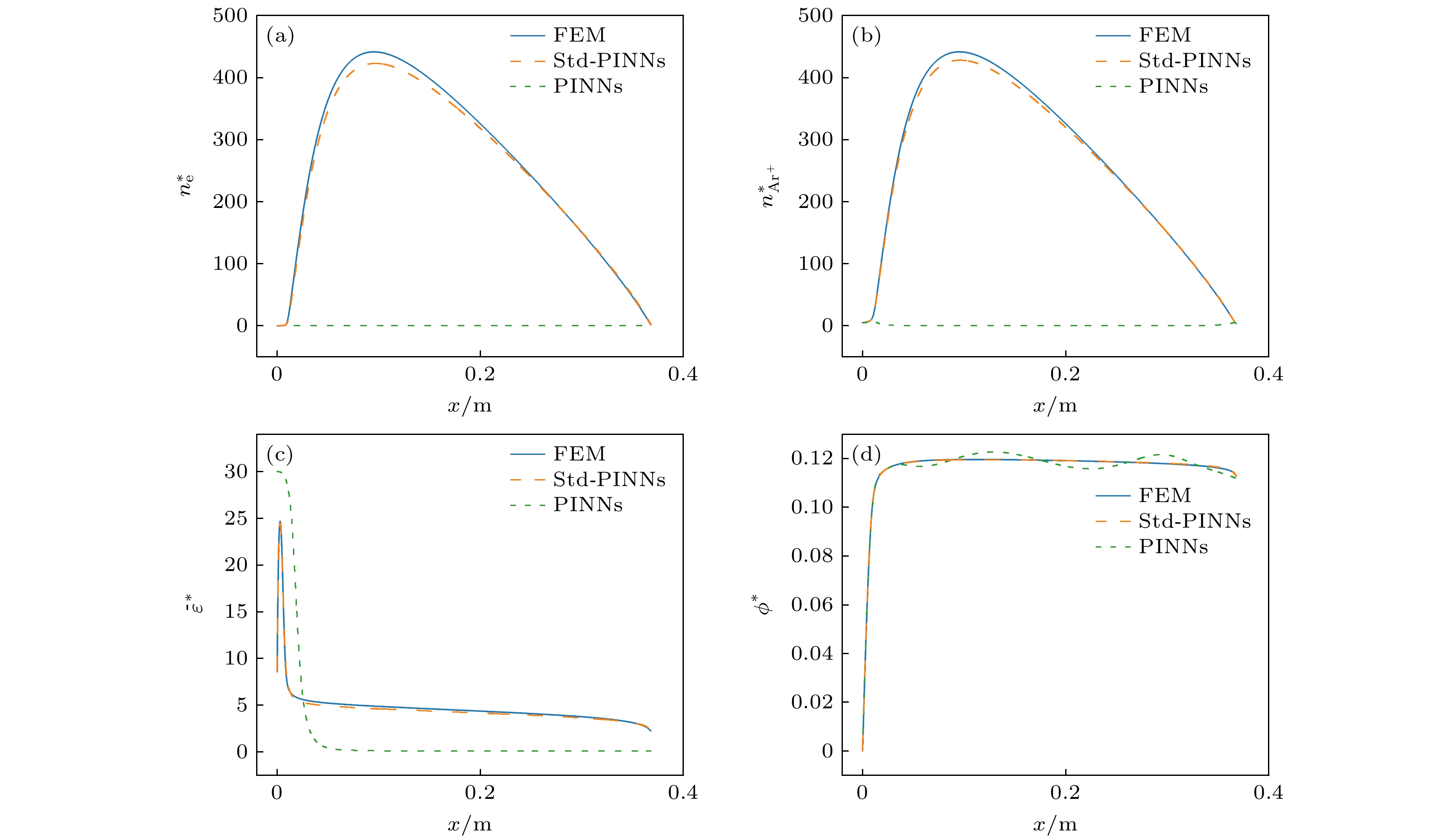
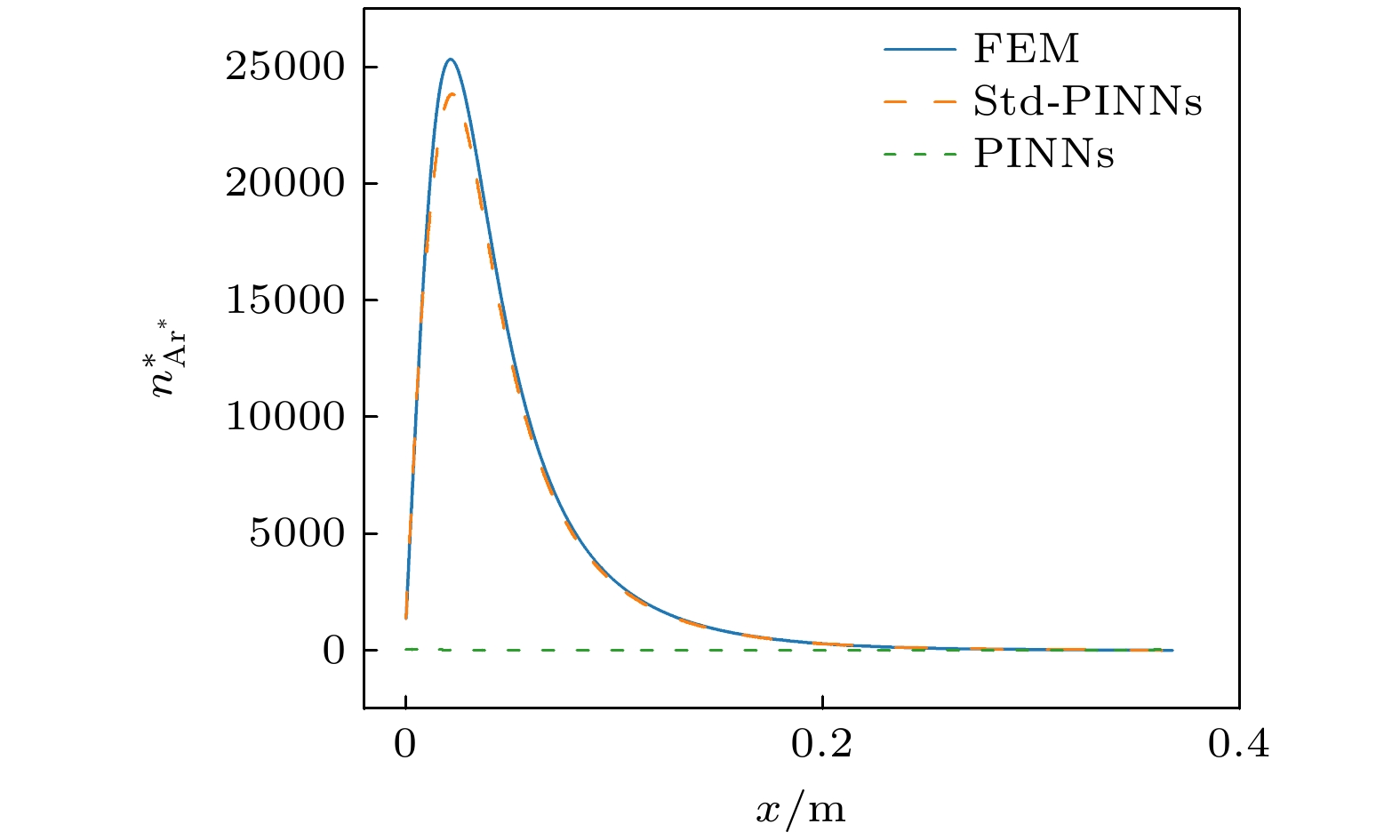
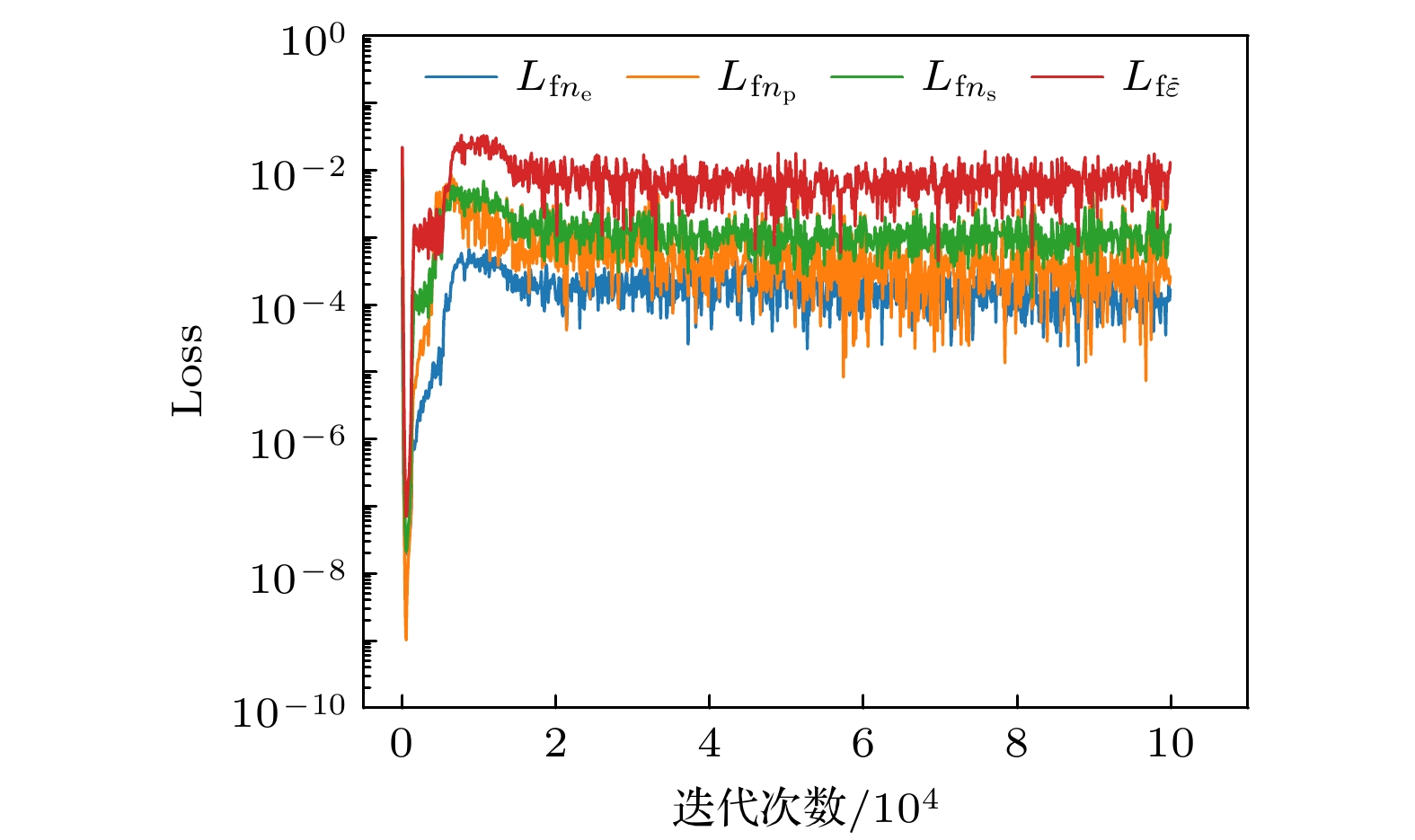
In recent years, the artificial intelligence computing paradigm represented by physics-informed neural networks (PINNs) has received great attention in the field of plasma numerical simulation. However, the plasma chemical system considered in related research is relatively simplified, and the research on solving the more complex multi-particle low-temperature fluid model based on PINNs is still blank. In more complex chemical systems, the coupling relationship between particle densities and between particle densities and mean electron energy become more intricate. Therefore, the applicability of PINNs in dealing with sophisticated reaction systems needs further exploring and improving. In this work, we propose a general PINN framework (source term decoupled PINNs, Std-PINNs) for solving multi-particle low-temperature plasma fluid model. By introducing equivalent positive ions and replacing each particle transport equation with the current continuity equation as a physical constraint, Std-PINN splits the entire solution process into the training processes of two neural networks, realizing the decoupling of the source term of the heavy particle transport equation from the electron density and mean electron energy, which greatly reduces the complexity of neural network training. In this work, the application of Std-PINNs to solving multi-particle low-temperature plasma fluid models is demonstrated through two classic discharge cases with different complexity of reaction systems (low-pressure argon glow discharge and atmospheric-pressure helium glow discharge) and the performance of Std-PINN is compared with that of conventional PINN and finite element method (FEM). The results show that the training results output from the traditional PINN are completely incorrect due to the strong coupling correlation of each physical variable through the source terms of each particle transport equation, while the L₂ relative error between Std-PINN and FEM results can reach up to ~10^–2 , thus verifying the feasibility of Std-PINN in simulating multi-particle plasma fluid model. Std-PINN expands the application of deep learning method to modeling complex physical systems and provides new ideas for conducting low-temperature plasma simulations. In addition, this study provides novel insights into the field of artificial intelligence scientific computing: the mathematical form that describes the state of a physical system is not unique. By introducing equivalent physical variables, equations suitable for neural network solutions can be derived and combined with observable data to simplify problems.

Keywords:

Authors and contacts

School of Electric Power, South China University of Technology, Guangzhou 510641, China

Corresponding author: Dai Dong, ddai@scut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 52377145).

FullText HTML : translate this paragraph

References

[1]	Sanito R C, You S J, Wang Y F 2021 J. Environ. Manage. 288 112380 Google Scholar
[2]	Cheng H, Xu J X, Li X, Liu D W, Lu X P 2020 Phys. Plasmas 27 063514 Google Scholar
[3]	Han Z J, Murdock A T, Seo D H, Bendavid A 2018 2D Mater. 5 032002 Google Scholar
[4]	Lazarou C, Belmonte T, Chiper A S, Georghiou G E 2016 Plasma Sources Sci. Technol. 25 055023 Google Scholar
[5]	Guikema J, Miller N, Niehof J, Klein M, Walhout M 2000 Phys. Rev. Lett. 85 3817 Google Scholar
[6]	Fang Z, Wang X J, Shao T, Zhang C 2017 IEEE Trans. Plasma Sci. 45 310 Google Scholar
[7]	Trelles J P 2016 J. Phys. D: Appl. Phys. 49 393002 Google Scholar
[8]	Purwins H G 2011 IEEE Trans. Plasma Sci. 39 2112 Google Scholar
[9]	Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sci. Technol. 21 074003 Google Scholar
[10]	Wang Q, Zhou X Y, Dai D, Huang Z E, Zhang D M 2021 Plasma Sources Sci. Technol. 30 05LT01 Google Scholar
[11]	Wang Q, Ning W J, Dai D, Zhang Y H 2020 Plasma Process. Polym. 17 e1900182 Google Scholar
[12]	Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sources Sci. Technol. 28 104001 Google Scholar
[13]	Biel W, Albanese R, Ambrosino R, et al. 2019 Fus. Eng. Des. 146 465 Google Scholar
[14]	Logg A 2007 Archives of Computational Methods in Engineering (Vol.14) (Berlin: Springer) pp93–138 Google Scholar
[15]	Eymard R, Gallouët T, Herbin R 2000 Handbook of Numerical Analysis (Vol. 7) (Amsterdam: Elsevier) pp713– 1018 Google Scholar
[16]	Bogaerts A, Tu X, Whitehead J C, Centi G, Lefferts L, Guaitella O, Azzolina-Jury F, Kim H H, Murphy A B, Schneider W F 2020 J. Phys. D: Appl. Phys. 53 443001 Google Scholar
[17]	Neyts E C 2016 Plasma Chem. Plasma Process. 36 185 Google Scholar
[18]	Mei D H, Zhu X B, Wu C F, Ashford B, Williams P T, Tu X 2016 Appl. Catal. B 182 525 Google Scholar
[19]	Yi Y H, Li S K, Cui Z L, Hao Y Z, Zhang Y, Wang L, Liu P, Tu X, Xu X M, Guo H C, Bogaerts A 2021 Appl. Catal. B 296 120384 Google Scholar
[20]	Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686 Google Scholar
[21]	Raissi M, Yazdani A, Karniadakis G E 2020 Science 367 1026 Google Scholar
[22]	De Florio M, Schiassi E, Ganapol B D, Furfaro R 2021 Phys. Fluids 33 047110 Google Scholar
[23]	Arzani A, Wang J X, D’Souza R M 2021 Phys. Fluids 33 071905 Google Scholar
[24]	Kawaguchi S, Takahashi K, Ohkama H, Satoh K 2020 Plasma Sources Sci. Technol. 29 025021 Google Scholar
[25]	Cai S Z, Wang Z C, Wang S F, Perdikaris P, Karniadakis G E 2021 J. Heat Transfer 143 102719 Google Scholar
[26]	Laubscher R 2021 Phys. Fluids 33 087101 Google Scholar
[27]	Mathews A, Francisquez M, Hughes J W, Hatch D R, Zhu B, Rogers B N 2021 Phys. Rev. E 104 025205 Google Scholar
[28]	Zhong L L, Gu Q, Wu B Y 2020 Comput. Phys. Commun. 257 107496 Google Scholar
[29]	Zhong L L, Wu B Y, Wang Y 2022 Phys. Fluids 34 087116 Google Scholar
[30]	Wan J, Wang Q, Dai D, Ning W J 2019 Phys. Plasmas 26 103510 Google Scholar
[31]	Wang Q, Ning W J, Dai D, Zhang Y H, Ouyang J 2019 J. Phys. D: Appl. Phys. 52 205201 Google Scholar
[32]	Glorot X, Bengio Y 2010 Proceedings of the 13th International Conference on Artificial Intelligence and Statistics Sardinia, Italy, May 13–15, 2010 pp249–256
[33]	Liu D C, Nocedal J 1989 Math. Program. 45 503 Google Scholar
[34]	Kingma D P, Ba J L 2014 arXiv: 1412.6980 [cs. LG]
[35]	Wang S, Yu X, Perdikaris P 2022 J. Comput. Phys. 449 110768 Google Scholar
[36]	Hagelaar G J M, Kroesen G M W 2000 J. Comput. Phys. 159 1 Google Scholar
[37]	Blickle V, Speck T, Lutz C, Seifert U, Bechinger C 2007 Phys. Rev. Lett. 98 210601 Google Scholar
[38]	Hagelaar G J M, Pitchford L C 2005 Plasma Sources Sci. Technol. 14 722 Google Scholar
[39]	Wang Q, Economou D J, Donnelly V M 2006 J. Appl. Phys. 100 023301 Google Scholar
[40]	Dyatko N A, Ionikh Y Z, Kochetov I V, Marinov D L, Meshchanov A V, Napartovich A P, Petrov F B, Starostin S A 2008 J. Phys. D: Appl. Phys. 41 055204 Google Scholar
[41]	Deloche R, Monchicourt P, Cheret M, Lambert F 1976 Phys. Rev. A 13 1140 Google Scholar
[42]	Hagelaar G J M, De Hoog F J, Kroesen G M W 2000 Phys. Rev. E 62 1452 Google Scholar
[43]	Hassé H R, Cook W R 1931 Philos. Mag. J. Sci. 12 554 Google Scholar
[44]	Staack D, Farouk B, Gutsol A, Fridman A 2005 Plasma Sources Sci. Technol. 14 700 Google Scholar
[45]	Wang Q, Dai D, Ning W J, Zhang Y H 2021 J. Phys. D: Appl. Phys. 54 115203 Google Scholar
[46]	Tochikubo F, Shirai N, Uchida S 2011 Appl. Phys. Express 4 056001 Google Scholar
[47]	Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sources Sci. Technol. 28 075003 Google Scholar
[48]	Pitchford L C, Alves L L, Bartschat K, et al. 2017 Plasma Process. Polym. 14 1600098 Google Scholar
[49]	Zhu X M, Pu Y K 2009 J. Phys. D: Appl. Phys. 43 015204 Google Scholar
[50]	Riccardi C, Barni R 2012 Chem. Kinet. 10 38396 Google Scholar
[51]	Liu D X, Iza F, Wang X H, Ma Z Z, Rong M Z, Kong M G 2013 Plasma Sources Sci. Technol. 22 055016 Google Scholar
[52]	Zhu M R, Zhong A, Dai D, Wang Q, Shao T, Ostrikov K K 2022 J. Phys. D: Appl. Phys. 55 355201 Google Scholar
[53]	Pietanza L D, Guaitella O, Aquilanti V, et al 2021 Eur. Phys. J. D 75 237 Google Scholar

Cited By

图 1 一维辉光放电模型的几何结构

Figure 1. The geometry of the one-dimensional glow discharge model.

DownLoad: Full-Size Img PowerPoint

图 2 Std-PINNs结构示意图

Figure 2. Schematic diagram of the structure of the Std-PINNs.

DownLoad: Full-Size Img PowerPoint

图 3 FEM, Std-PINNs与传统PINNs的数值结果比较(NN₁输出)

Figure 3. Comparison of the numerical results of FEM, Std-PINNs (the output of NN₁) and traditional PINNs.

DownLoad: Full-Size Img PowerPoint

图 4 FEM, Std-PINNs与传统PINNs的数值结果比较 (NN₂输出)

Figure 4. Comparison of the numerical results of FEM, Std-PINNs (the output of NN₂) and traditional PINNs.

DownLoad: Full-Size Img PowerPoint

图 5 应用传统PINNs时, 整个迭代过程中粒子输运方程与电子能量密度方程的损失函数值

Figure 5. When the traditional PINNs is applied, the loss function values of the particle transport equation and the electron energy density equation during the whole iteration.

DownLoad: Full-Size Img PowerPoint

图 6 应用传统PINNs时, 整个迭代过程中各粒子数密度与平均电子能量的相对L₂误差

Figure 6. When the traditional PINNs is applied, the relative L₂ error of each particle number density and mean electron energy during the whole iteration.

DownLoad: Full-Size Img PowerPoint

图 7 FEM, Std-PINNs (NN₁输出)与传统PINNs的数值结果比较

Figure 7. Comparison of the numerical results between the FEM, the Std-PINNs (the output of NN₁) and traditional PINNs.

DownLoad: Full-Size Img PowerPoint

图 8 FEM, Std-PINNs(NN₂输出)与传统PINNs的数值结果比较

Figure 8. Comparison of the numerical results between the FEM, the Std-PINNs (the output of NN₂) and traditional PINNs.

DownLoad: Full-Size Img PowerPoint

表 A1 各案例基准值

Table A1. Reference values for each case.

案例	${n_0}$/m^–3	${\phi _0}$/V	${\bar \varepsilon _0}$/eV	${L_0}$/m
1	1×10¹³	1×10³	1	1×10^–2
2	5×10¹⁷	1×10³	1	1×10^–4

DownLoad: CSV

表 1 低气压氩气辉光放电的碰撞反应

Table 1. Collision reaction of low pressure argon glow discharge.

序号	反应方程	速率常数	焓/eV	参考文献
1	e + Ar $\Rightarrow $ e + Ar	f ($ \overline{\boldsymbol{\varepsilon}} $)	—	[48]
2	e + Ar $\Rightarrow $ e + Ar^*	f ($ \overline{\boldsymbol{\varepsilon}} $)	11.5	[48]
3	e + Ar $\Rightarrow $ 2e + Ar⁺	f ($ \overline{\boldsymbol{\varepsilon}} $)	15.8	[48]
4	e + Ar^* $\Rightarrow $ 2e + Ar⁺	f ($ \overline{\boldsymbol{\varepsilon}} $)	4.43	[48]
5	Ar^* + Ar^* $\Rightarrow $ e + Ar+ Ar⁺	6.2×10^–16	—	[40]
6	Ar^* + Ar $\Rightarrow $ Ar+ Ar	3×10^–21	—	[40]
注: 表中f($ \overline{\boldsymbol{\varepsilon}} $)代表电子碰撞反应的速率常数, 为平均电子能的函数, 通过向Bolsig⁺导入电子碰撞反应截面数据计算得到; 双体反应的速率常数单位为m³/s.

DownLoad: CSV

表 2 大气压氦气辉光放电的碰撞反应

Table 2. Collision reaction of atmospheric pressure helium glow discharge.

序号	反应方程	速率常数	焓/eV	参考文献
1	e + He $\Rightarrow $ e + He	f ($ \overline{\boldsymbol{\varepsilon}} $)	—	[48]
2	e + He $\Rightarrow $ e + He^*	f ($ \overline{\boldsymbol{\varepsilon}} $)	19.8	[48]
3	e + He $\Rightarrow $ 2e + He⁺	f ($ \overline{\boldsymbol{\varepsilon}} $)	24.6	[48]
4	e + He^* $\Rightarrow $ 2e + He⁺	$1.28 \times 10^{-13}\times T_{\rm e}^{0.6}\times \exp(-4.78/T_{\rm e}) $	4.8	[41]
5	e + He^* $\Rightarrow $ e + He	2.9 × 10^–15	–19.8	[41]
6	e + ${\mathrm{He}}_2^* $ $\Rightarrow $ e + 2He	3.8 × 10^–15	–17.9	[39]
7	2e + He⁺ $\Rightarrow $ e + He^*	6.0 × 10^–32 × (T_e/0.026)^–4.4	–4.8	[4]
8	2e + ${\mathrm{He}}_2^+ $ $\Rightarrow $ e + He + He^*	4.0 × 10^–32 × (T_e/0.026)^–1	—	[39]
9	e + He+ ${\mathrm{He}}_2^+ $ $\Rightarrow $2He + He^*	5 × 10^–39 × (T_e/0.026)^–1	—	[39]
10	2e + ${\mathrm{He}}_2^+ $ $\Rightarrow $ e + ${\mathrm{He}}_2^* $	4.0 × 10^–32 × (T_e/0.026)^–1	—	[39]
11	e + He+ He⁺ $\Rightarrow $ He + He^*	5.0 × 10^–39 × (T_e/0.026)^–1	—	[39]
12	e + He+ ${\mathrm{He}}_2^+ $ $\Rightarrow $ He + ${\mathrm{He}}_2^* $	1.0 × 10^–38 × (T_e/0.026)^–2	—	[39]
13	e + ${\mathrm{He}}_2^* $ $\Rightarrow $ 2e + ${\mathrm{He}}_2^+ $	5.0 × 10^–15 × (T_e/0.026)^–1	3.4	[39]
14	He^* + 2He $\Rightarrow $ 3He	2.0 × 10^–46	—	[39]
15	2He^* $\Rightarrow $ e + ${\mathrm{He}}_2^+ $	2.9 × 10^–15	—	[39]
16	2He + He⁺ $\Rightarrow $ He + ${\mathrm{He}}_2^+ $	1.4 × 10^–43	—	[4]
17	2He + He^* $\Rightarrow $ ${\mathrm{He}}_2^* $ + He	2 × 10^–46	—	[4]
18	He^* + ${\mathrm{He}}_2^* $ $\Rightarrow $ e + ${\mathrm{He}}_2^+ $ + He	5 × 10^–16	—	[4]
19	${\mathrm{He}}_2^* $ + ${\mathrm{He}}_2^* $ $\Rightarrow $ e + ${\mathrm{He}}_2^+ $ + 2He	1.2 × 10^–15	—	[4]
20	${\mathrm{He}}_2^* $ + He $\Rightarrow $ 3He	1.5 × 10^–21	—	[4]
注: 表中He^代表He(2³S)及He(2¹S), He₂^则代表He₂(${\rm a}{}^3\Sigma_{\rm u}^+ $) .

DownLoad: CSV

map

[1]	Sanito R C, You S J, Wang Y F 2021 J. Environ. Manage. 288 112380 Google Scholar
[2]	Cheng H, Xu J X, Li X, Liu D W, Lu X P 2020 Phys. Plasmas 27 063514 Google Scholar
[3]	Han Z J, Murdock A T, Seo D H, Bendavid A 2018 2D Mater. 5 032002 Google Scholar
[4]	Lazarou C, Belmonte T, Chiper A S, Georghiou G E 2016 Plasma Sources Sci. Technol. 25 055023 Google Scholar
[5]	Guikema J, Miller N, Niehof J, Klein M, Walhout M 2000 Phys. Rev. Lett. 85 3817 Google Scholar
[6]	Fang Z, Wang X J, Shao T, Zhang C 2017 IEEE Trans. Plasma Sci. 45 310 Google Scholar
[7]	Trelles J P 2016 J. Phys. D: Appl. Phys. 49 393002 Google Scholar
[8]	Purwins H G 2011 IEEE Trans. Plasma Sci. 39 2112 Google Scholar
[9]	Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sci. Technol. 21 074003 Google Scholar
[10]	Wang Q, Zhou X Y, Dai D, Huang Z E, Zhang D M 2021 Plasma Sources Sci. Technol. 30 05LT01 Google Scholar
[11]	Wang Q, Ning W J, Dai D, Zhang Y H 2020 Plasma Process. Polym. 17 e1900182 Google Scholar
[12]	Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sources Sci. Technol. 28 104001 Google Scholar
[13]	Biel W, Albanese R, Ambrosino R, et al. 2019 Fus. Eng. Des. 146 465 Google Scholar
[14]	Logg A 2007 Archives of Computational Methods in Engineering (Vol.14) (Berlin: Springer) pp93–138 Google Scholar
[15]	Eymard R, Gallouët T, Herbin R 2000 Handbook of Numerical Analysis (Vol. 7) (Amsterdam: Elsevier) pp713– 1018 Google Scholar
[16]	Bogaerts A, Tu X, Whitehead J C, Centi G, Lefferts L, Guaitella O, Azzolina-Jury F, Kim H H, Murphy A B, Schneider W F 2020 J. Phys. D: Appl. Phys. 53 443001 Google Scholar
[17]	Neyts E C 2016 Plasma Chem. Plasma Process. 36 185 Google Scholar
[18]	Mei D H, Zhu X B, Wu C F, Ashford B, Williams P T, Tu X 2016 Appl. Catal. B 182 525 Google Scholar
[19]	Yi Y H, Li S K, Cui Z L, Hao Y Z, Zhang Y, Wang L, Liu P, Tu X, Xu X M, Guo H C, Bogaerts A 2021 Appl. Catal. B 296 120384 Google Scholar
[20]	Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686 Google Scholar
[21]	Raissi M, Yazdani A, Karniadakis G E 2020 Science 367 1026 Google Scholar
[22]	De Florio M, Schiassi E, Ganapol B D, Furfaro R 2021 Phys. Fluids 33 047110 Google Scholar
[23]	Arzani A, Wang J X, D’Souza R M 2021 Phys. Fluids 33 071905 Google Scholar
[24]	Kawaguchi S, Takahashi K, Ohkama H, Satoh K 2020 Plasma Sources Sci. Technol. 29 025021 Google Scholar
[25]	Cai S Z, Wang Z C, Wang S F, Perdikaris P, Karniadakis G E 2021 J. Heat Transfer 143 102719 Google Scholar
[26]	Laubscher R 2021 Phys. Fluids 33 087101 Google Scholar
[27]	Mathews A, Francisquez M, Hughes J W, Hatch D R, Zhu B, Rogers B N 2021 Phys. Rev. E 104 025205 Google Scholar
[28]	Zhong L L, Gu Q, Wu B Y 2020 Comput. Phys. Commun. 257 107496 Google Scholar
[29]	Zhong L L, Wu B Y, Wang Y 2022 Phys. Fluids 34 087116 Google Scholar
[30]	Wan J, Wang Q, Dai D, Ning W J 2019 Phys. Plasmas 26 103510 Google Scholar
[31]	Wang Q, Ning W J, Dai D, Zhang Y H, Ouyang J 2019 J. Phys. D: Appl. Phys. 52 205201 Google Scholar
[32]	Glorot X, Bengio Y 2010 Proceedings of the 13th International Conference on Artificial Intelligence and Statistics Sardinia, Italy, May 13–15, 2010 pp249–256
[33]	Liu D C, Nocedal J 1989 Math. Program. 45 503 Google Scholar
[34]	Kingma D P, Ba J L 2014 arXiv: 1412.6980 [cs. LG]
[35]	Wang S, Yu X, Perdikaris P 2022 J. Comput. Phys. 449 110768 Google Scholar
[36]	Hagelaar G J M, Kroesen G M W 2000 J. Comput. Phys. 159 1 Google Scholar
[37]	Blickle V, Speck T, Lutz C, Seifert U, Bechinger C 2007 Phys. Rev. Lett. 98 210601 Google Scholar
[38]	Hagelaar G J M, Pitchford L C 2005 Plasma Sources Sci. Technol. 14 722 Google Scholar
[39]	Wang Q, Economou D J, Donnelly V M 2006 J. Appl. Phys. 100 023301 Google Scholar
[40]	Dyatko N A, Ionikh Y Z, Kochetov I V, Marinov D L, Meshchanov A V, Napartovich A P, Petrov F B, Starostin S A 2008 J. Phys. D: Appl. Phys. 41 055204 Google Scholar
[41]	Deloche R, Monchicourt P, Cheret M, Lambert F 1976 Phys. Rev. A 13 1140 Google Scholar
[42]	Hagelaar G J M, De Hoog F J, Kroesen G M W 2000 Phys. Rev. E 62 1452 Google Scholar
[43]	Hassé H R, Cook W R 1931 Philos. Mag. J. Sci. 12 554 Google Scholar
[44]	Staack D, Farouk B, Gutsol A, Fridman A 2005 Plasma Sources Sci. Technol. 14 700 Google Scholar
[45]	Wang Q, Dai D, Ning W J, Zhang Y H 2021 J. Phys. D: Appl. Phys. 54 115203 Google Scholar
[46]	Tochikubo F, Shirai N, Uchida S 2011 Appl. Phys. Express 4 056001 Google Scholar
[47]	Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sources Sci. Technol. 28 075003 Google Scholar
[48]	Pitchford L C, Alves L L, Bartschat K, et al. 2017 Plasma Process. Polym. 14 1600098 Google Scholar
[49]	Zhu X M, Pu Y K 2009 J. Phys. D: Appl. Phys. 43 015204 Google Scholar
[50]	Riccardi C, Barni R 2012 Chem. Kinet. 10 38396 Google Scholar
[51]	Liu D X, Iza F, Wang X H, Ma Z Z, Rong M Z, Kong M G 2013 Plasma Sources Sci. Technol. 22 055016 Google Scholar
[52]	Zhu M R, Zhong A, Dai D, Wang Q, Shao T, Ostrikov K K 2022 J. Phys. D: Appl. Phys. 55 355201 Google Scholar
[53]	Pietanza L D, Guaitella O, Aquilanti V, et al 2021 Eur. Phys. J. D 75 237 Google Scholar

[1]	Chen Jin-Feng, Zhu Lin-Fan. Electron collision cross section data in plasma etching modeling. Acta Physica Sinica, 2024, 73(9): 095201. doi: 10.7498/aps.73.20231598
[2]	Zhang Dong-He-Yu, Liu Jin-Bao, Fu Yang-Yang. Multiphysics modeling and simulations of laser-sustained plasmas. Acta Physica Sinica, 2024, 73(2): 025201. doi: 10.7498/aps.73.20231056
[3]	Wang Qian, Fan Yuan-Yuan, Zhao Jiang-Shan, Liu Bin, Qi Yan, Yan Bo-Xia, Wang Yan-Wei, Zhou Mi, Han Zhe, Cui Hui-Rong. Analysis of preionization effect of excimer laser. Acta Physica Sinica, 2023, 72(19): 194201. doi: 10.7498/aps.72.20230731
[4]	Tian Shi-Fang, Li Biao. Solving complex nonlinear problems based on gradient-optimized physics-informed neural networks. Acta Physica Sinica, 2023, 72(10): 100202. doi: 10.7498/aps.72.20222381
[5]	Wu Jian, Han Wen, Cheng Zhen-Zhen, Yang Bin, Sun Li-Li, Wang Di, Zhu Cheng-Peng, Zhang Yong, Geng Ming-Xin, Jing Yan. Structure optimization of carbon nanotube ionization sensor based on fluid model. Acta Physica Sinica, 2021, 70(9): 090701. doi: 10.7498/aps.70.20201828
[6]	Zhang Quan-Zhi, Zhang Lei-Yu, Ma Fang-Fang, Wang You-Nian. Cryogenic etching of porous material. Acta Physica Sinica, 2021, 70(9): 098104. doi: 10.7498/aps.70.20202245
[7]	He Shou-Jie, Zhou Jia, Qu Yu-Xiao, Zhang Bao-Ming, Zhang Ya, Li Qing. Simulation on complex dynamics of hollow cathode discharge in argon. Acta Physica Sinica, 2019, 68(21): 215101. doi: 10.7498/aps.68.20190734
[8]	Zhao Yue-Feng, Wang Chao, Wang Wei-Zong, Li Li, Sun Hao, Shao Tao, Pan Jie. Numerical simulation on particle density and reaction pathways in methane needle-plane discharge plasma at atmospheric pressure. Acta Physica Sinica, 2018, 67(8): 085202. doi: 10.7498/aps.67.20172192
[9]	Sun An-Bang, Li Han-Wei, Xu Peng, Zhang Guan-Jun. Monte Carlo simulations of electron transport coefficients in low temperature streamer discharge plasmas. Acta Physica Sinica, 2017, 66(19): 195101. doi: 10.7498/aps.66.195101
[10]	Wang Xue-Yang, Qi Zhi-Hua, Song Ying, Liu Dong-Ping. Bacteria sterilization application by using plasma activated physiological saline. Acta Physica Sinica, 2016, 65(12): 123301. doi: 10.7498/aps.65.123301
[11]	Dong Ye, Dong Zhi-Wei, Zhou Qian-Hong, Yang Wen-Yuan, Zhou Hai-Jing. Ionization parameters of high power microwave flashover on dielectric window surface calculated by particle-in-cell simulation for fluid modeling. Acta Physica Sinica, 2014, 63(6): 067901. doi: 10.7498/aps.63.067901
[12]	He Man-Li, Wang Xiao, Zhang Ming, Wang Li, Song Rui. Vibrational distribution of H2 (D2 and T2) molecules in low temperature plasma. Acta Physica Sinica, 2014, 63(12): 125201. doi: 10.7498/aps.63.125201
[13]	Zhao Peng-Cheng, Liao Cheng, Yang Dang, Zhong Xuan-Ming, Lin Wen-Bin. High power microwave breakdown in gas using the fluid model with non-equilibrium electron energy distribution function. Acta Physica Sinica, 2013, 62(5): 055101. doi: 10.7498/aps.62.055101
[14]	Liu Fu-Cheng, Yan Wen, Wang De-Zhen. Two-dimensional simulation of atmospheric pressure cold plasma jets in a needle-plane electrode configuration. Acta Physica Sinica, 2013, 62(17): 175204. doi: 10.7498/aps.62.175204
[15]	Zhang Zeng-Hui, Zhang Guan-Jun, Shao Xian-Jun, Chang Zheng-Shi, Peng Zhao-Yu, Xu Hao. Modelling study of dielectric barrier glow discharge in Ar/NH3 mixture at atmospheric pressure. Acta Physica Sinica, 2012, 61(24): 245205. doi: 10.7498/aps.61.245205
[16]	Zhang Zeng-Hui, Shao Xian-Jun, Zhang Guan-Jun, Li Ya-Xi, Peng Zhao-Yu. One-dimensional simulation of dielectric barrier glow discharge in atmospheric pressure Ar. Acta Physica Sinica, 2012, 61(4): 045205. doi: 10.7498/aps.61.045205
[17]	Shao Xian-Jun, Ma Yue, Li Ya-Xi, Zhang Guan-Jun. One-dimensional simulation of low pressure xenon dielectric barrier discharge. Acta Physica Sinica, 2010, 59(12): 8747-8754. doi: 10.7498/aps.59.8747
[18]	Zhou Li-Na, Wang Xin-Bing. A fluid model for the simulation of discharges in microhollow cathode. Acta Physica Sinica, 2004, 53(10): 3440-3446. doi: 10.7498/aps.53.3440
[19]	Liu Cheng Sen, Wang De Zhen. Plasma source ion implantation near the end of a cylindrical bore using an auxiliary electrode for finite rise time voltage pulses. Acta Physica Sinica, 2003, 52(1): 109-114. doi: 10.7498/aps.52.109
[20]	LIU HONG-XIANG, WEI HE-LIN, LIU ZU-LI, LIU YAN-HONG, WANG JUN-ZHEN. EFFECT OF THE MAGNETIC MIRROR FIELD ON THE ION ENERGY DISTRIBUTIONS IN A RADIO F REQUENCY PLASMA. Acta Physica Sinica, 2000, 49(9): 1764-1768. doi: 10.7498/aps.49.1764

Catalog

Vol. 73, Issue 14 - 2024-07-20

Metrics

Abstract views: 1350
PDF Downloads: 42
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板