-
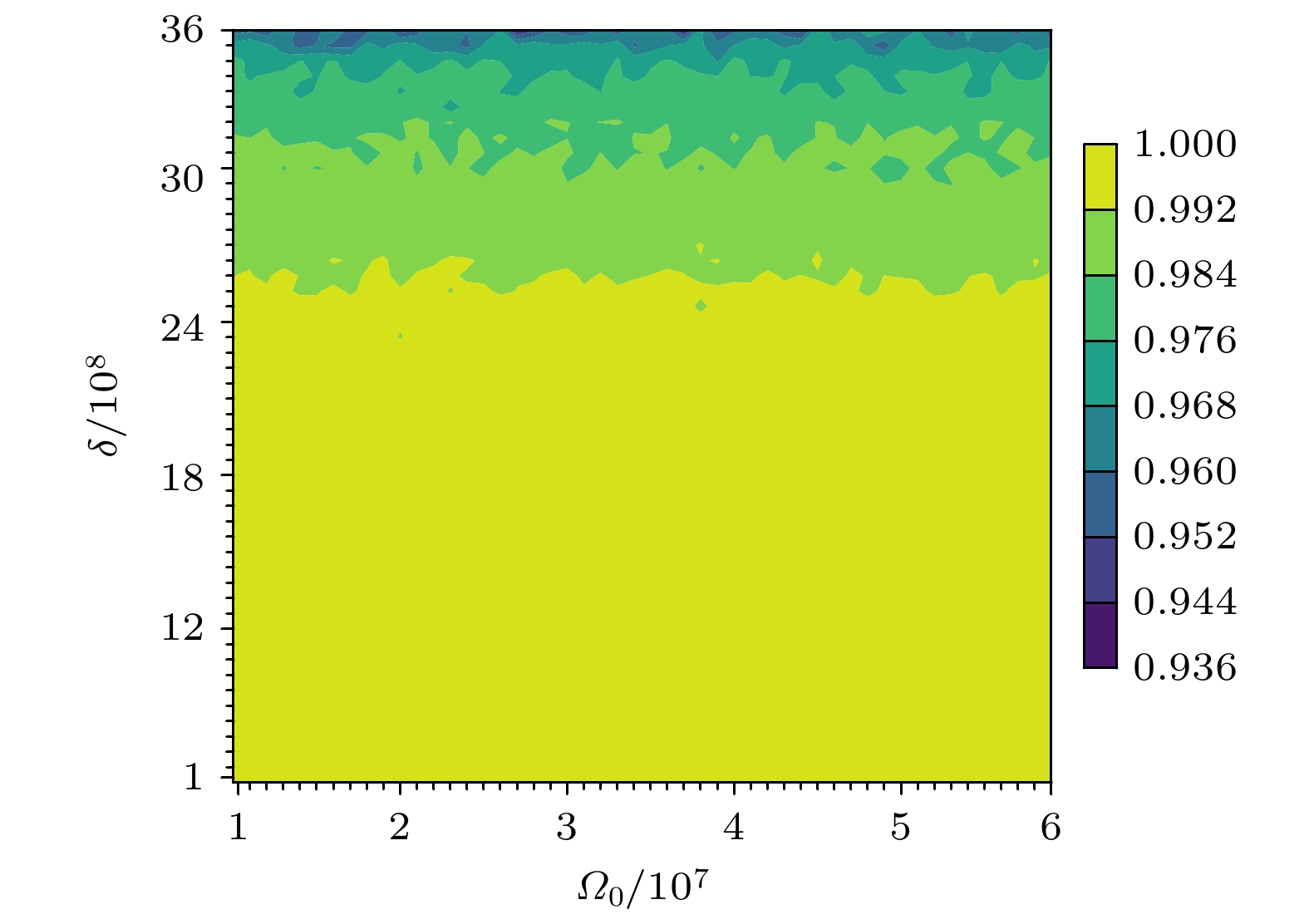
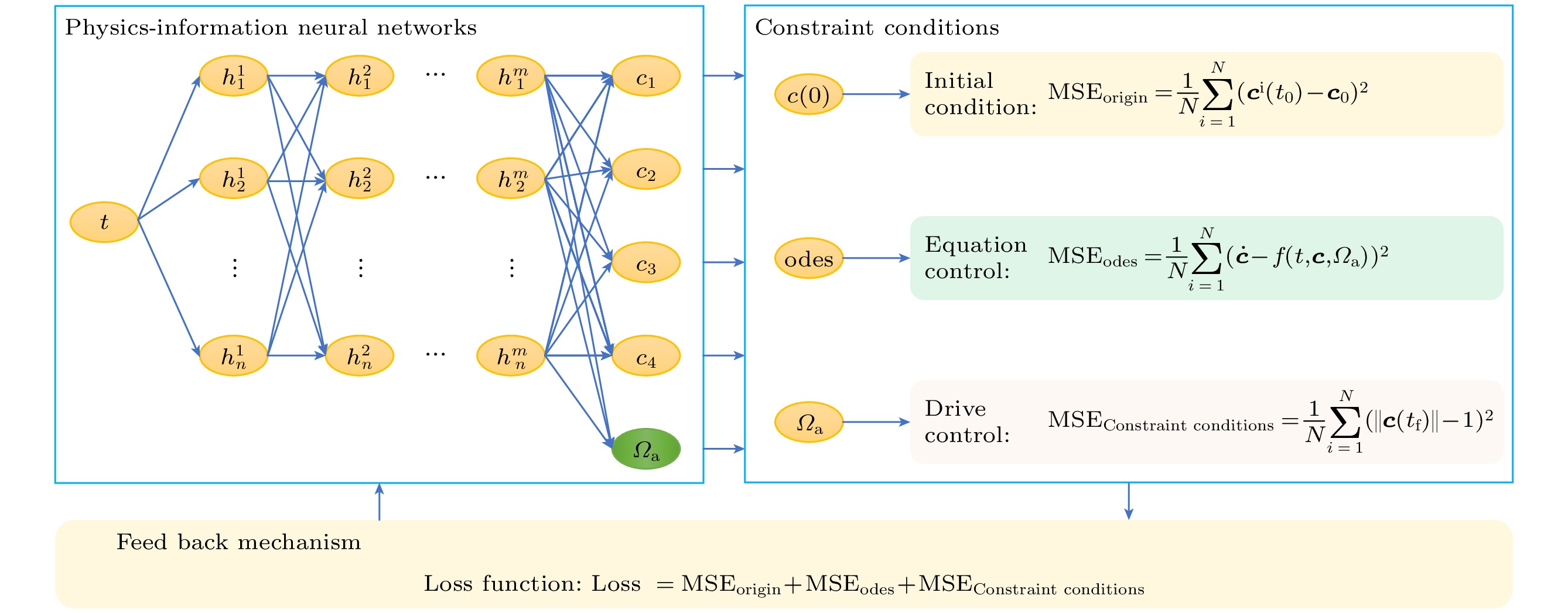
A quantum shortcut to adiabaticity scheme based on physics-informed neural networks is proposed in this work. Compared with traditional shortcut to adiabaticity technology, our method innovatively integrates machine learning methods by employing parameterized physics-informed neural networks to solve parameterized differential equations. The neural networks serve as an approximating function for quantum adiabatic evolution processes, while incorporating parameter-dependent differential equations and various physical constraints as components of the loss function. Through networks training, we effectively simulate quantum system dynamics and derive the driving control field for population inversion. Numerical simulations show that the quantum system can achieve rapid population inversion within significantly reduced time while maintaining high fidelity and exceptional robustness against parameter fluctuations. The neural networks exhibit remarkable computational capabilities, particularly suitable for generating control functions in complex quantum systems. Compared with conventional counter-diabatic driving and transitionless quantum driving methods, this PINN-based framework not only achieves better control performance but also provides the improved practicality for experimental implementations. The success of this method demonstrates its promising applications in quantum control tasks, including but not limited to quantum state preparation, quantum gate optimization, and adiabatic quantum computing acceleration.
-
Keywords:
- shortcuts to adiabaticity /
- deep learning /
- physics-informed neural networks /
- differential equation
[1] Vitanov N V, Halfmann T, Shore B W 2001 Annu Rev. Phys. Chem. 52 763
 Google Scholar
Google Scholar
[2] Law C K, Eberly J H 1996 Phys. Rev. Lett. 76 1055
 Google Scholar
Google Scholar
[3] Kuhn A, Hennrich M, Bondo T 1999 Appl Phys. B 69 373
 Google Scholar
Google Scholar
[4] Torosov B T, Guérin S, Vitanov N V 2011 Phys. Rev. Lett. 106 233001
 Google Scholar
Google Scholar
[5] Brif C, Chakrabarti R, Rabitz H 2010 New J. Phys. 12 075008
 Google Scholar
Google Scholar
[6] Demirplak M, Rice S A 2002 J. Chem. Phys. 116 8028
 Google Scholar
Google Scholar
[7] del Campo A 2011 Phys. Rev. A 84 031606
 Google Scholar
Google Scholar
[8] del Campo A 2013 Phys. Rev. Lett. 111 100502
 Google Scholar
Google Scholar
[9] Tian L 2012 Phys. Rev. Lett. 108 153604
 Google Scholar
Google Scholar
[10] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303
 Google Scholar
Google Scholar
[11] Ibáñez S, Li Y C, Chen X 2015 Phys. Rev. A 92 062136
 Google Scholar
Google Scholar
[12] Song X K, Ai Q, Qiu J 2016 Phys. Rev. A 93 052324
 Google Scholar
Google Scholar
[13] Liu S, Chen Y H, Wang Y 2022 Phys. Rev. A 106 042430
 Google Scholar
Google Scholar
[14] Masuda S, Nakamura K 2008 Phys. Rev. A 78 062108
 Google Scholar
Google Scholar
[15] Masuda S, Nakamura K 2011 Phys. Rev. A 84 043434
 Google Scholar
Google Scholar
[16] Zhu J J, Chen X 2021 Phys. Rev. A 103 023307
 Google Scholar
Google Scholar
[17] Luo D W, Pyshkin P, Lam C H 2015 Phys. Rev. A 92 062127
 Google Scholar
Google Scholar
[18] Kang Y H, Chen Y H, Huang B H 2017 Ann. Phys. 529 1700004
 Google Scholar
Google Scholar
[19] Torrontegui E, Martínez-Garaot S, Muga J 2014 Phys. Rev. A 89 043408
 Google Scholar
Google Scholar
[20] Güngördü U, Wan Y, FasihiM A 2012 Phys. Rev. A 86 062312
 Google Scholar
Google Scholar
[21] 张瑶, 张云波, 陈立 2021 70 168702
 Google Scholar
Google Scholar
Zhang Y, Zhang Y B, Chen L 2021 Acta Phys. Sin. 70 168702
 Google Scholar
Google Scholar
[22] 田十方, 李彪 2023 72 100202
 Google Scholar
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
 Google Scholar
Google Scholar
[23] 方波浪, 王建国, 冯国斌 2022 71 200601
 Google Scholar
Google Scholar
Fang B L, Wang J G, Feng G B 2022 Acta Phys. Sin. 71 200601
 Google Scholar
Google Scholar
[24] Cai Y H, He Y L, Lang S N, Cui X B, Zhang X Q, Yao Z J 2025 Comput. Geosci. 196 105857
 Google Scholar
Google Scholar
[25] Nursyiva I, Maharani A B, Fatimah N H, Sugiyarto S, Danang A P 2025 Results Appl. Math. 25 100539
 Google Scholar
Google Scholar
[26] Ko T, Kim D, Park J, Lee S H 2025 Appl. Energy 382 125318
 Google Scholar
Google Scholar
[27] Zheng J C, Yang Y L 2024 Appl. Soft Comput. 167 112370
 Google Scholar
Google Scholar
[28] Chen X, Peng W Q 2025 Commun. Theor. Phys. 77 025002
 Google Scholar
Google Scholar
[29] Roy A, Chatterjee T, Adhikari S 2024 Probab. Eng. Mech. 78 103701
 Google Scholar
Google Scholar
[30] Han J, Jentzen A, Weinan E 2018 Proc. Natl. Acad. Sci. U. S. A 115 8505
 Google Scholar
Google Scholar
[31] Rudy H S, Brunton L S, Proctor L J, Kutz N 2017 Sci. Adv. 3 e1602614
 Google Scholar
Google Scholar
[32] Raissi M, Karniadakis G E 2018 J. Comput. Phys. 357 125
 Google Scholar
Google Scholar
[33] Li J, Chen Y 2021 Commun. Theor. Phys. 73 015001
 Google Scholar
Google Scholar
[34] Pu J C, Li J, Chen Y 2021 Nonlinear Dyn. 105 1723
[35] Pu J C, Chen Y 2022 Chaos, Solitons Fractals 160 112182
 Google Scholar
Google Scholar
[36] Lin S N, Chen Y 2022 J. Comput. Phys. 457 111053
 Google Scholar
Google Scholar
[37] Ding Y C, Ban Y, Martín J, Solano E, Casanova J, Chen X 2021 Phys. Rev. A 103 L040401
 Google Scholar
Google Scholar
[38] Norambuena A, Mattheakis M, González F, Coto R 2024 Phys. Rev. Lett 132 010801
 Google Scholar
Google Scholar
-
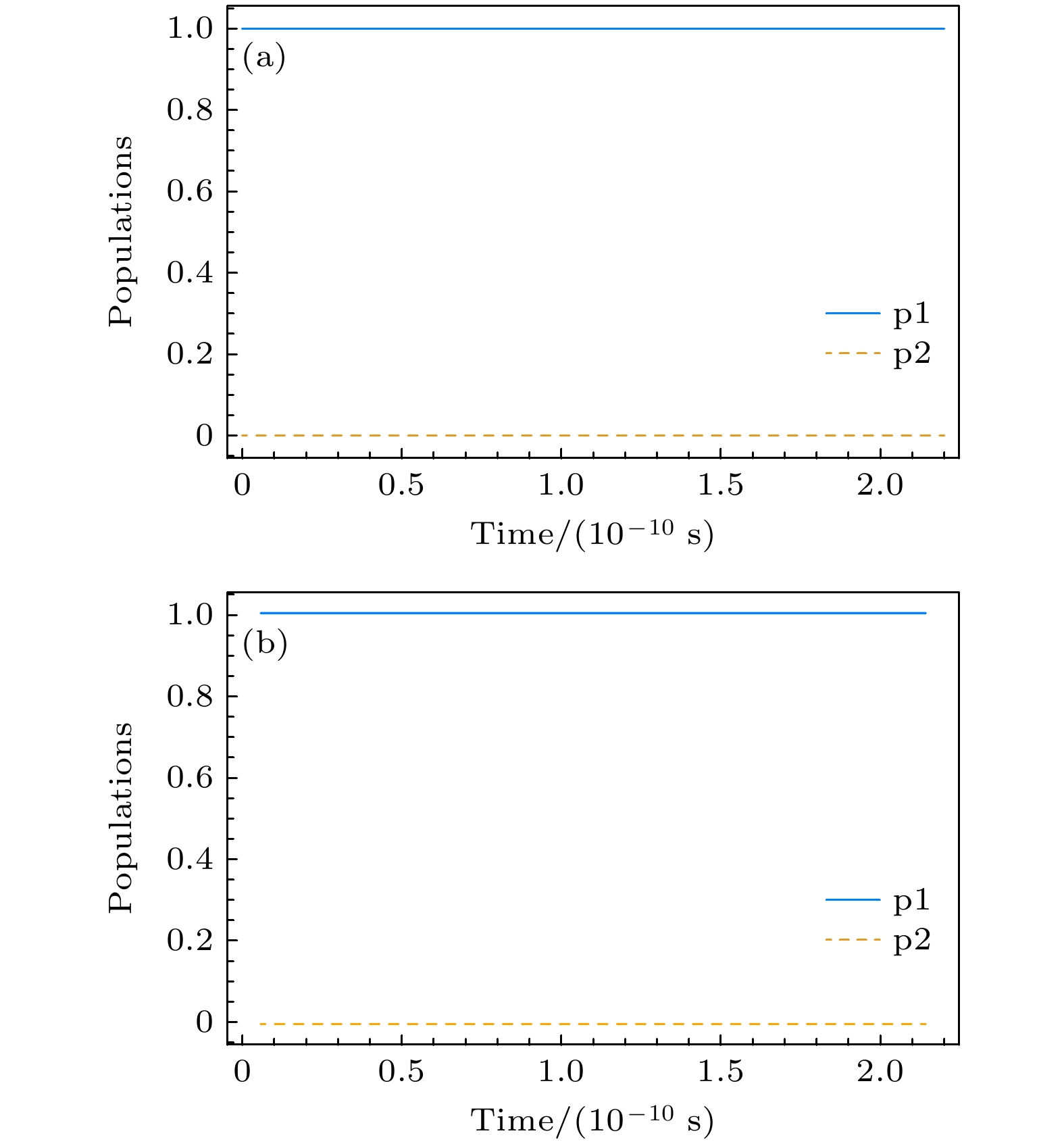
图 2 PINN方法仿真和Mathematica软件仿真无驱动布居转移情况对比图 (a) PINN仿真无驱动布居转移; (b) Mathematica软件中无驱动布居转移的仿真. 参数选取为: $ {t_0} = $$ 5 \times {10^{ - 12}} {\text{ s}}, \;{t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}}, \;{\varOmega _0} = 10 {\text{ MHz}}, \;\delta = 600 {\text{ }} {\text{MHz}} $
Figure 2. Comparison between PINN method simulation and Mathematica software simulation of undriven population transfer: (a) PINN simulated undriven population transfer; (b) simulation of undriven population transfer in Mathematica software. The parameters are selected as: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}}, \;{t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}}, \;{\varOmega _0} = 10 {\text{ MHz}}, \;\delta = 600 {\text{ MHz}} $.
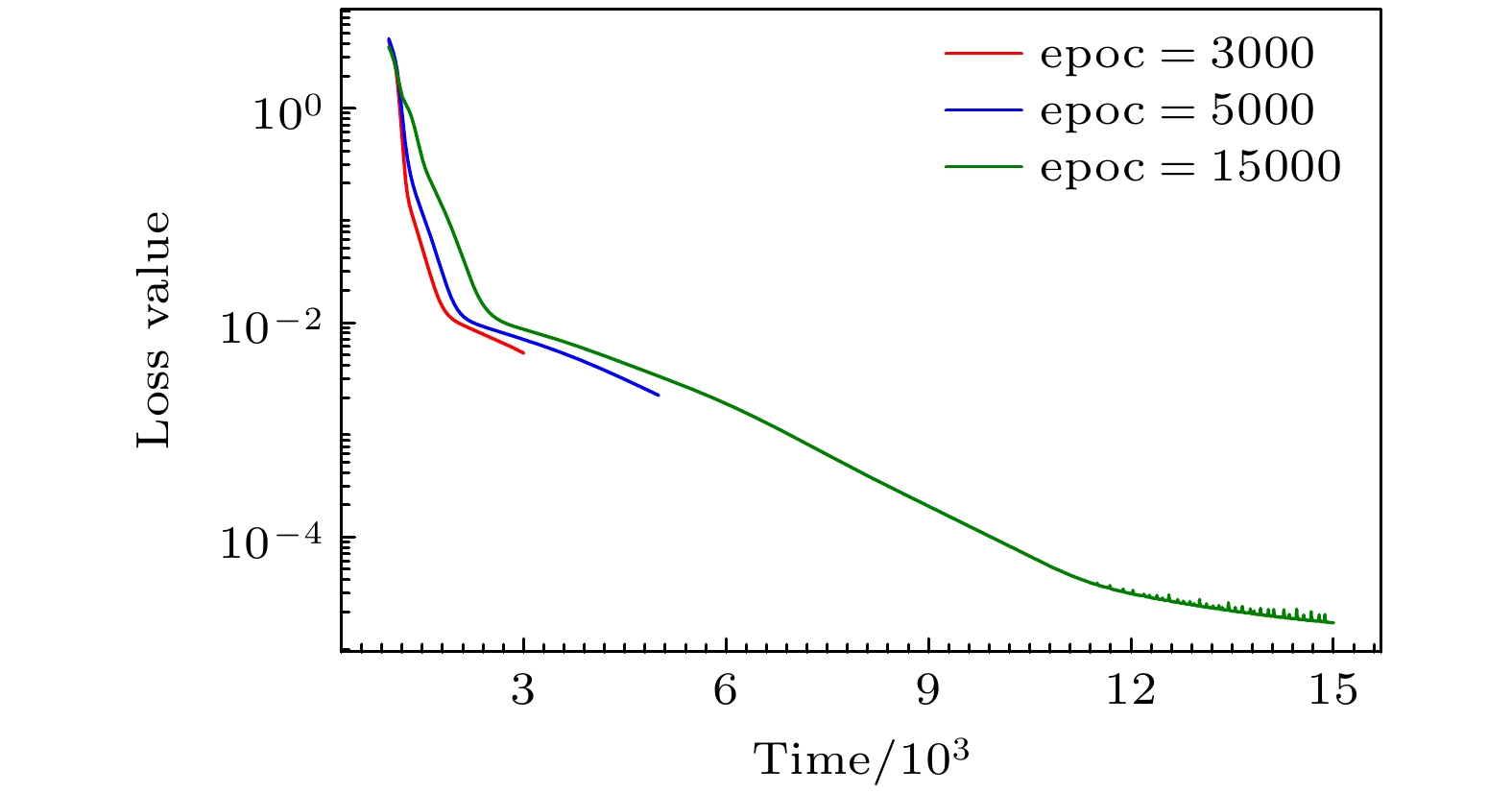
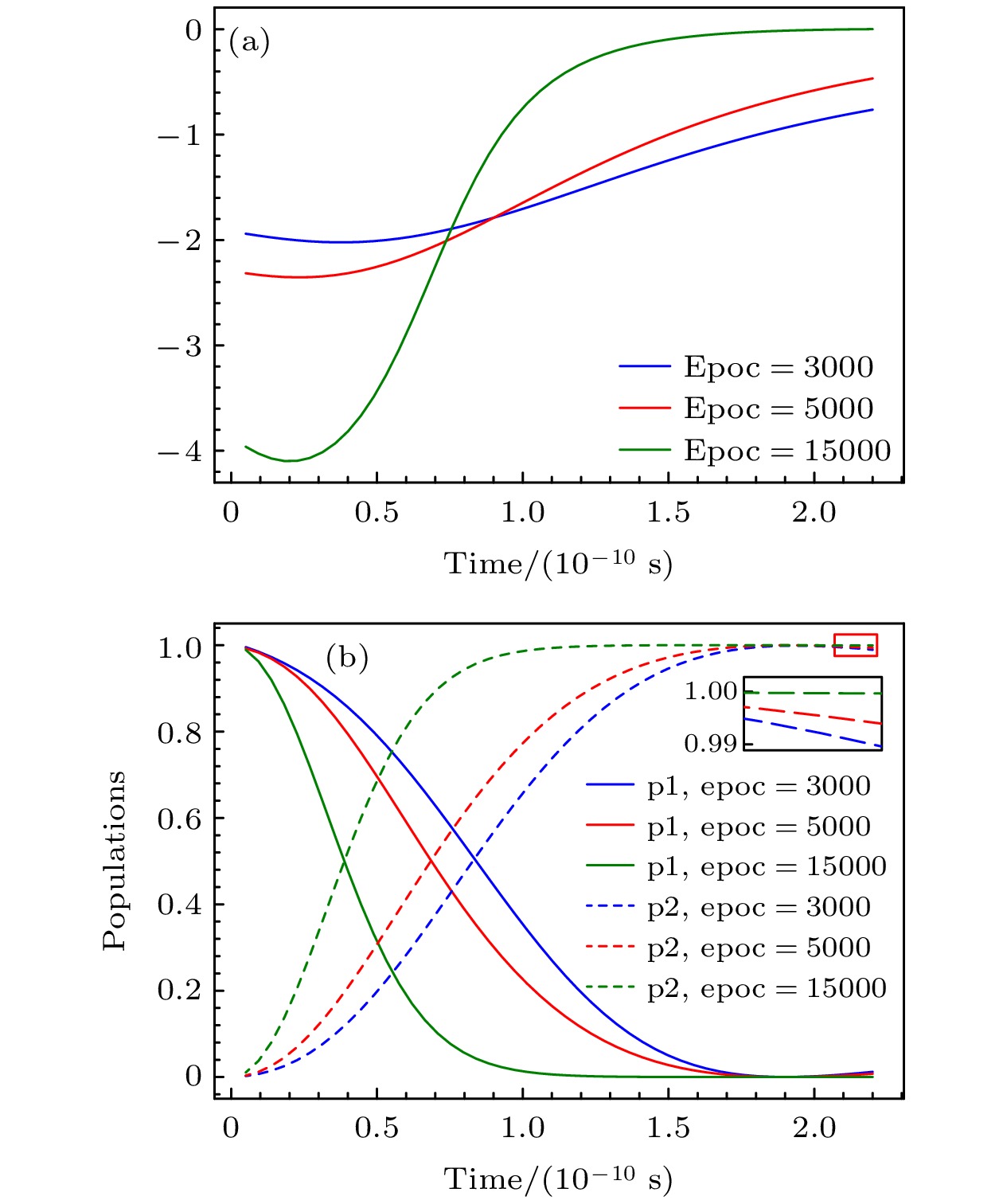
图 3 不同训练次数下的损失函数曲线图. 参数选取为$ {t_0} = 5 \times {10^{ - 12}} {\text{ s}}$, $ {t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, $ {\varOmega _0} = 10 {\text{ MHz}}$, $\delta = $$ 600 {\text{ MHz}} $
Figure 3. Loss function curves under different training times. The parameters are selected as: $ {t_0} = 5 \times {10^{ - 12}} {\text{ s}}, \;{t_{\text{f}}} = 2 \times $$ {10^{ - 10}} {\text{ s}}$, $ {\varOmega _0} = 10 {\text{ MHz}}, \;\delta = 600 {\text{ MHz}} $.
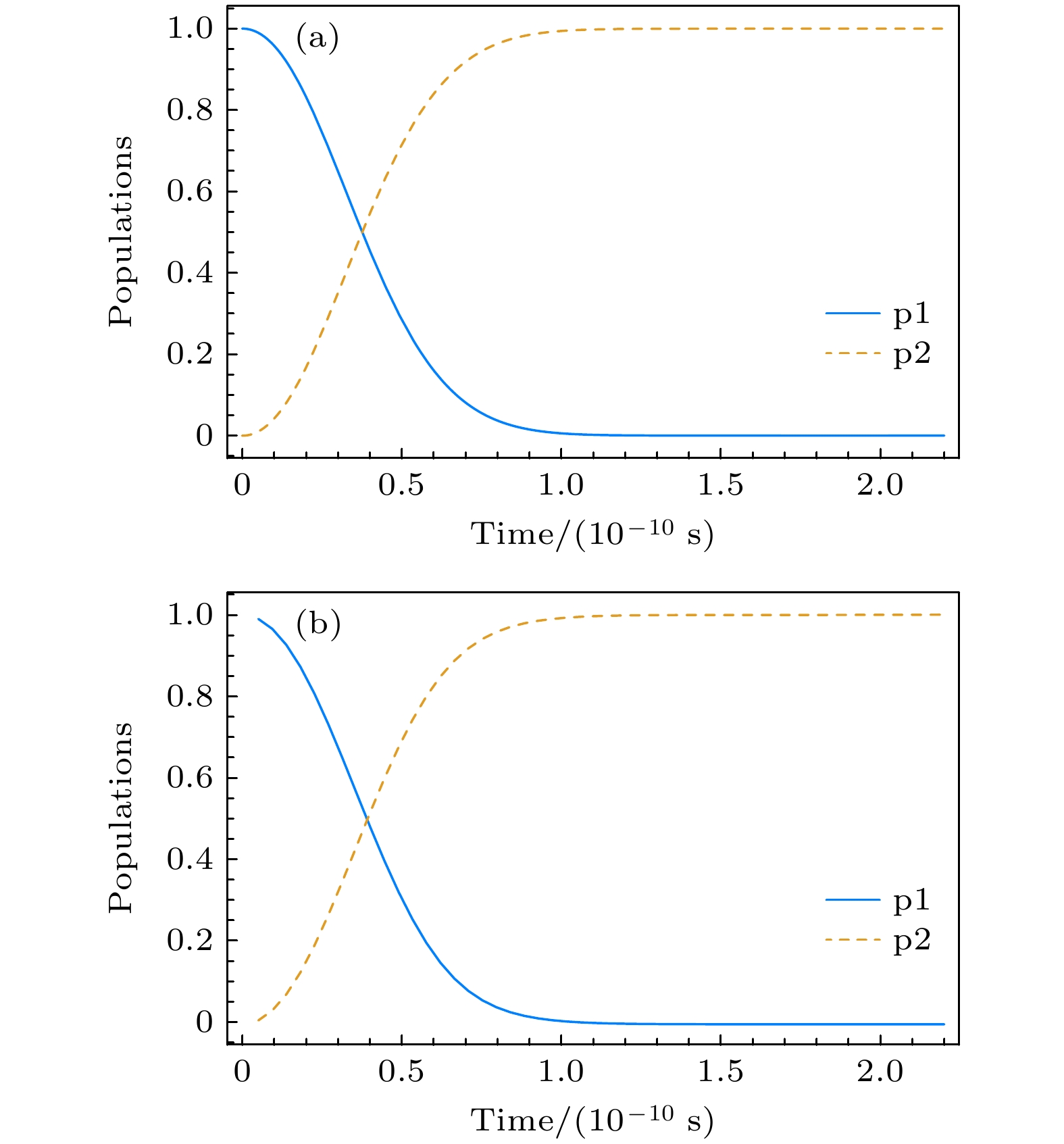
图 4 STAPINN方法和Mathematica软件仿真加驱动的布居转移情况对比 (a) STAPINN仿真加驱动的布居转移情况; (b) Mathematica仿真加驱动的布居转移情况. 参数选取为: ${t_0} = 5 \times {10^{ - 12}} {\text{ s}} $, $ {t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $
Figure 4. Comparison of driver population transfer after STAPINN method and Mathematica software simulation and optimization: (a) STAPINN simulation optimization drives population transfer; (b) population transfer driven by Mathematica simulation optimization. The parameters are selected as: $ {t_0} = 5 \times {10^{ - 12}} {\text{ s}}$, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = $$ 10 {\text{ MHz}}$, $\delta = 600 {\text{ MHz}} $.
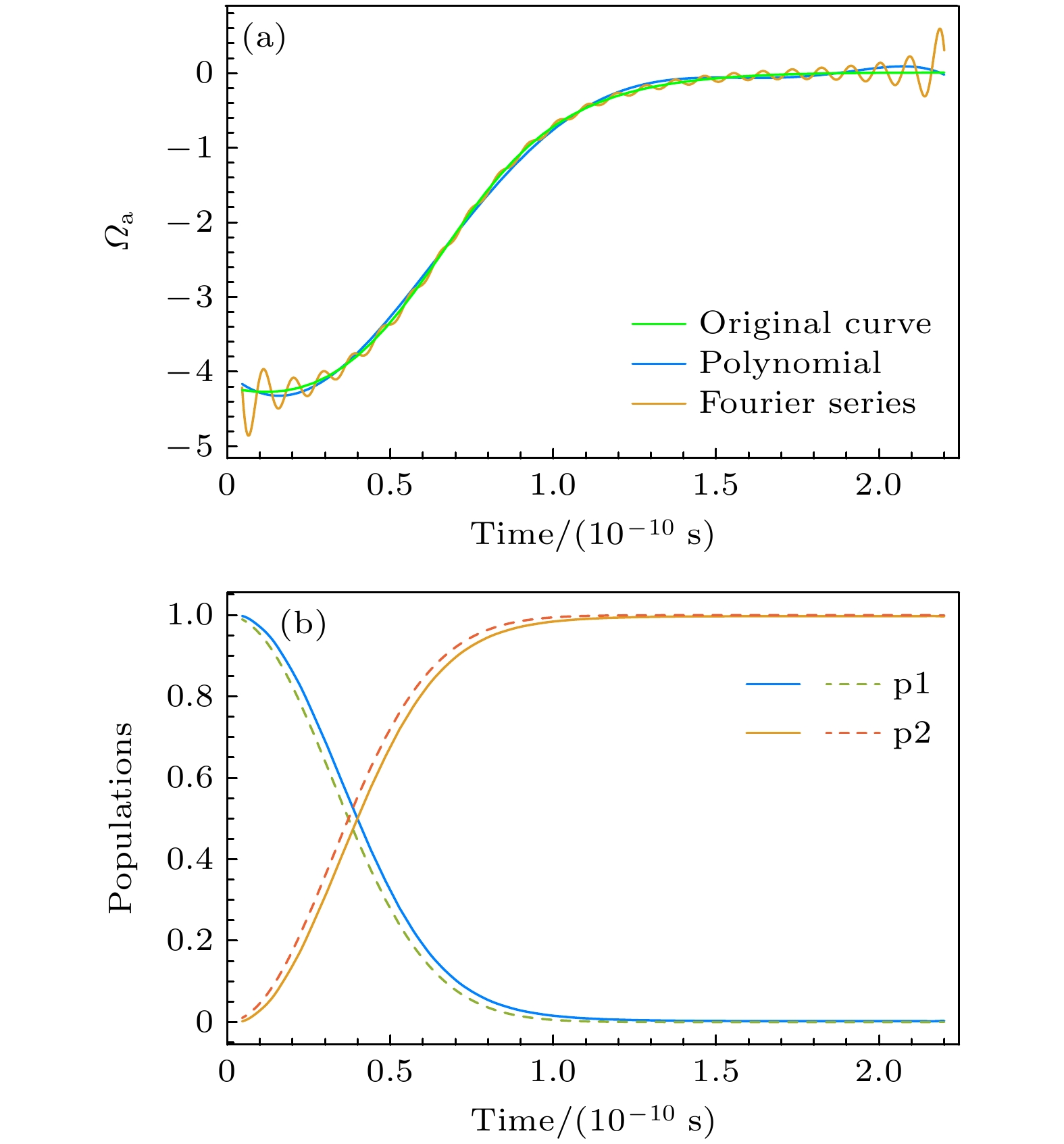
图 5 (a)多项式展开的驱动函数和傅里叶级数展开的驱动函数对比图; (b)利用Mathematica软件模拟此驱动下的布居转移情况, 蓝色和褐色实线为傅里叶级数展开的驱动函数对应的布居数反转曲线, 红色和绿色虚线为多项式展开的驱动函数对应的布居反转曲线. 参数选取为: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}} $, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $
Figure 5. (a) Comparison between the driver function of polynomial expansion and the driver function of Fourier series expansion; (b) using Mathematica software to simulate the population transfer under this drive, the blue and brown solid lines are the population inversion curves corresponding to the driver function of Fourier series expansion, and the red and green dashed lines are the population inversion curves corresponding to the driver function of polynomial expansion. The parameters are selected as: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}} $, ${t_{\text{f}}} = 2 \times $$ {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $.
图 6 (a)不同训练次数下的驱动曲线图; (b)不同训练次数下的驱动实现的布居转移情况对比图. 参数选取为: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}}$, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600 {\text{ MHz}} $
Figure 6. (a) Drive curves under different training times; (b) comparison diagram of population transfer of the drive under different training times. Set the parameter to: $ {t_0} = 5 \times $$ {10^{ - 12}} {\text{ s}}$, ${t_{\text{f}}} = 2 \times {10^{ - 10}} {\text{ s}} $, ${\varOmega _0} = 10 {\text{ MHz}} $, $\delta = 600{\text{ }} {\text{ MHz}} $
-
[1] Vitanov N V, Halfmann T, Shore B W 2001 Annu Rev. Phys. Chem. 52 763
 Google Scholar
Google Scholar
[2] Law C K, Eberly J H 1996 Phys. Rev. Lett. 76 1055
 Google Scholar
Google Scholar
[3] Kuhn A, Hennrich M, Bondo T 1999 Appl Phys. B 69 373
 Google Scholar
Google Scholar
[4] Torosov B T, Guérin S, Vitanov N V 2011 Phys. Rev. Lett. 106 233001
 Google Scholar
Google Scholar
[5] Brif C, Chakrabarti R, Rabitz H 2010 New J. Phys. 12 075008
 Google Scholar
Google Scholar
[6] Demirplak M, Rice S A 2002 J. Chem. Phys. 116 8028
 Google Scholar
Google Scholar
[7] del Campo A 2011 Phys. Rev. A 84 031606
 Google Scholar
Google Scholar
[8] del Campo A 2013 Phys. Rev. Lett. 111 100502
 Google Scholar
Google Scholar
[9] Tian L 2012 Phys. Rev. Lett. 108 153604
 Google Scholar
Google Scholar
[10] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303
 Google Scholar
Google Scholar
[11] Ibáñez S, Li Y C, Chen X 2015 Phys. Rev. A 92 062136
 Google Scholar
Google Scholar
[12] Song X K, Ai Q, Qiu J 2016 Phys. Rev. A 93 052324
 Google Scholar
Google Scholar
[13] Liu S, Chen Y H, Wang Y 2022 Phys. Rev. A 106 042430
 Google Scholar
Google Scholar
[14] Masuda S, Nakamura K 2008 Phys. Rev. A 78 062108
 Google Scholar
Google Scholar
[15] Masuda S, Nakamura K 2011 Phys. Rev. A 84 043434
 Google Scholar
Google Scholar
[16] Zhu J J, Chen X 2021 Phys. Rev. A 103 023307
 Google Scholar
Google Scholar
[17] Luo D W, Pyshkin P, Lam C H 2015 Phys. Rev. A 92 062127
 Google Scholar
Google Scholar
[18] Kang Y H, Chen Y H, Huang B H 2017 Ann. Phys. 529 1700004
 Google Scholar
Google Scholar
[19] Torrontegui E, Martínez-Garaot S, Muga J 2014 Phys. Rev. A 89 043408
 Google Scholar
Google Scholar
[20] Güngördü U, Wan Y, FasihiM A 2012 Phys. Rev. A 86 062312
 Google Scholar
Google Scholar
[21] 张瑶, 张云波, 陈立 2021 70 168702
 Google Scholar
Google Scholar
Zhang Y, Zhang Y B, Chen L 2021 Acta Phys. Sin. 70 168702
 Google Scholar
Google Scholar
[22] 田十方, 李彪 2023 72 100202
 Google Scholar
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
 Google Scholar
Google Scholar
[23] 方波浪, 王建国, 冯国斌 2022 71 200601
 Google Scholar
Google Scholar
Fang B L, Wang J G, Feng G B 2022 Acta Phys. Sin. 71 200601
 Google Scholar
Google Scholar
[24] Cai Y H, He Y L, Lang S N, Cui X B, Zhang X Q, Yao Z J 2025 Comput. Geosci. 196 105857
 Google Scholar
Google Scholar
[25] Nursyiva I, Maharani A B, Fatimah N H, Sugiyarto S, Danang A P 2025 Results Appl. Math. 25 100539
 Google Scholar
Google Scholar
[26] Ko T, Kim D, Park J, Lee S H 2025 Appl. Energy 382 125318
 Google Scholar
Google Scholar
[27] Zheng J C, Yang Y L 2024 Appl. Soft Comput. 167 112370
 Google Scholar
Google Scholar
[28] Chen X, Peng W Q 2025 Commun. Theor. Phys. 77 025002
 Google Scholar
Google Scholar
[29] Roy A, Chatterjee T, Adhikari S 2024 Probab. Eng. Mech. 78 103701
 Google Scholar
Google Scholar
[30] Han J, Jentzen A, Weinan E 2018 Proc. Natl. Acad. Sci. U. S. A 115 8505
 Google Scholar
Google Scholar
[31] Rudy H S, Brunton L S, Proctor L J, Kutz N 2017 Sci. Adv. 3 e1602614
 Google Scholar
Google Scholar
[32] Raissi M, Karniadakis G E 2018 J. Comput. Phys. 357 125
 Google Scholar
Google Scholar
[33] Li J, Chen Y 2021 Commun. Theor. Phys. 73 015001
 Google Scholar
Google Scholar
[34] Pu J C, Li J, Chen Y 2021 Nonlinear Dyn. 105 1723
[35] Pu J C, Chen Y 2022 Chaos, Solitons Fractals 160 112182
 Google Scholar
Google Scholar
[36] Lin S N, Chen Y 2022 J. Comput. Phys. 457 111053
 Google Scholar
Google Scholar
[37] Ding Y C, Ban Y, Martín J, Solano E, Casanova J, Chen X 2021 Phys. Rev. A 103 L040401
 Google Scholar
Google Scholar
[38] Norambuena A, Mattheakis M, González F, Coto R 2024 Phys. Rev. Lett 132 010801
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 773
- PDF Downloads: 36
- Cited By: 0














 DownLoad:
DownLoad: