-
The three-dimensional density distribution of dust particles in complex plasma under microgravity condition has received much attention. Based on the three-dimensional hydrodynamic simulation, the influences of different coupling parameters, shielding parameters, charge of dust particles and plasma density on the Mach cone by laser-induced are studied in complex plasma under microgravity conditions. When the shielding parameters are large, it is found that three different formulas of coupling parameters
$ \varGamma = \dfrac{{Z_{\text{d}}^{2}{e^2}}}{{d \cdot {T_{\text{d}}}}} $ ,$ \varGamma ' = \dfrac{{Z_{\text{d}}^{2}{e^2}}}{{d \cdot {T_{\text{d}}}}}\exp ( - \kappa ) $ and$ \varGamma ' = \dfrac{{Z_{\text{d}}^{2}{e^2}}}{{d \cdot {T_{\text{d}}}}}(1{+}\kappa {+}\dfrac{{{\kappa ^2}}}{2})\exp ( - \kappa ) $ have a great influence on the disturbance density of dust particles, and the simulation results are in better agreement with the theoretical expectations under the third formulas. In addition, when the laser radiation force is parallel or vertical to the laser movement speed, the Mach cone structure is symmetrical or antisymmetric in the three-dimensional space, which is mainly based on the asymmetry of the laser disturbance mode. Besides, increasing the shielding parameters, or reducing the charge of dust particles, or reducing the plasma density, the shielding interaction between the dust particles is enhanced, making the Mach cone formed by the dust disturbance density more localized around the laser spot, which is characterized by narrowing the disturbance range and increasing density value. It is expected that this work can provide some reference for the theoretical and experimental studies of laser-induced Mach cone in three-dimensional complex plasma under microgravity conditions.[1] Selwyn G S, Singh J, Bennett R S 1989 J. Vac. Sci. Technol. , A 7 2758
Google Scholar
[2] Fortov V E, Khrapak A G, Khrapak S A, Molotkov V I, Petrov O F 2004 Phys. Usp. 47 447
Google Scholar
[3] Merlino R L, Goree J A 2004 Phys. Today 57 32
Google Scholar
[4] Markus H T, Hubertus M T, Christina A K, Andre M, Uwe K 2023 npj Microgravity 9 13
Google Scholar
[5] Zaehringer E, Schwabe M, Zhdanov S, Mohr D P, Knapek C A, Huber P, Semenov I L, Thomas H M 2018 Phys. Plasmas 25 033703
Google Scholar
[6] Samsonov D, Goree J, Ma Z W, Bhattacharjee A, Thomas H M, Morfill G E 1999 Phys. Rev. Lett. 83 3649
Google Scholar
[7] Ma Z W, Bhattacharjee A 2002 Phys. Plasmas 9 3349
Google Scholar
[8] Melzer A, Nunomura S, Samsonov D, Ma Z W, Goree J 2000 Phys. Rev. E 62 4162
Google Scholar
[9] Sato N, Uchida G, Kaneko T, Shimizu S, Iizuka S 2001 Phys. Plasmas 8 1786
Google Scholar
[10] Cheung F, Samarian A, James B 2003 New J. Phys. 5 75
Google Scholar
[11] Schwabe M, Jiang K, Zhdanov S, Hagl T, Huber P, Ivlev A V, Lipaev A M, Molotkov V I, Naumkin V N, Sutterlin K R, Thomas H M, Fortov V E, Morfill G E, Skvortsov A, Volkov S 2011 EPL 96 55001
Google Scholar
[12] Nosenko V, Goree J, Ma Z W, Piel A 2002 Phys. Rev. Lett. 88 135001
Google Scholar
[13] Nosenko V, Goree J, Ma Z W, Dubin D H E, Piel A 2003 Phys. Rev. E 68 056409
Google Scholar
[14] Hou L J, Wang Y N, Mišković Z L 2004 Phys. Rev. E 70 056406
Google Scholar
[15] 段蒙悦, 贾文柱, 张莹莹, 张逸凡, 宋远红 2023 72 165202
Google Scholar
Duan M Y, Jia W Z, Zhang Y Y, Zhang Y F, Song Y H 2023 Acta Phys. Sin. 72 165202
Google Scholar
[16] Jia W Z, Zhang Q Z, Wang X F, Song Y H, Zhang Y Y, Wang Y N 2019 J. Phys. D: Appl. Phys. 52 015206
Google Scholar
[17] Jiang K, Hou L J, Wang Y N 2005 Chin. Phys. Lett. 22 1713
Google Scholar
[18] Hou L J, Mišković Z L, Jiang K, Wang Y N 2006 Phys. Rev. Lett. 96 255005
Google Scholar
[19] Jiang K, Hou L J, Wang Y N, Mišković Z L 2006 Phys. Rev. E. 73 016404
Google Scholar
[20] Slattery W L, Doolen G D, DeWitt H E 1980 Phys. Rev. A 21 2087
Google Scholar
[21] Ichimaru S 1982 Rev. Mod. Phys. 54 1017
Google Scholar
[22] Hartmann P, Kalman G J, Donkó Z, Kutasi K 2005 Phys. Rev. E 72 026409
Google Scholar
[23] Vaulina O S, Khrapak S A, Morfill G 2002 Phys. Rev. E 66 016404
Google Scholar
[24] Wani R, Mir A, Batool F, Tiwari S 2022 Sci. Rep. 12 11557
Google Scholar
[25] Kaw P K, Sen A 1998 Phys. Plasmas 5 3552
Google Scholar
[26] Kalman G J, Rosenberg M, DeWitt H E 2000 Phys. Rev. Lett. 84 6030
Google Scholar
[27] Ikezi H 1986 Phys. Fluids 29 1764
Google Scholar
[28] Dasgupta C, Maitra S 2021 Phys. Plasmas 28 043703
Google Scholar
[29] Bandyopadhyay P, Dey R, Kadyan S, Sen A 2014 Phys. Plasmas 21 103707
Google Scholar
[30] Nunomura S, Zhdanov S, Samsonov D, Morfill G 2005 Phys. Rev. Lett. 94 045001
Google Scholar
[31] Vaulina O S, Vladimirov S V 2002 Phys. Plasmas 9 835
Google Scholar
[32] Fortov V E, Vaulina O S, Petrov O F, Molotkov V I, Lipaev A M, Torchinsky V M, Thomas H M, Morfill G E, Khrapak S A, Semenov Yu P, Ivanov A I, Krikalev S K, Kalery A Yu, Zaletin S V, Gidzenko Yu P 2003 Phys. Rev. Lett. 90 245005
Google Scholar
[33] Caliebe D, Arp O, Piel A 2011 Phys. Plasmas 18 073702
Google Scholar
[34] Vaulina O S, Khrapak S A 2000 J. Exp. Theor. Phys. 90 287
Google Scholar
[35] Hamaguchi S, Farouki R T, Dubin D H E 1997 Phys. Rev. E 56 4671
Google Scholar
[36] Epstein P S 1924 Phys. Rev. 23 710
Google Scholar
[37] Slattery W L, Doolen G D, DeWitt H E 1982 Phys. Rev. A 26 2255
Google Scholar
[38] Dubin D 2000 Phys. Plasmas 7 3895
Google Scholar
-
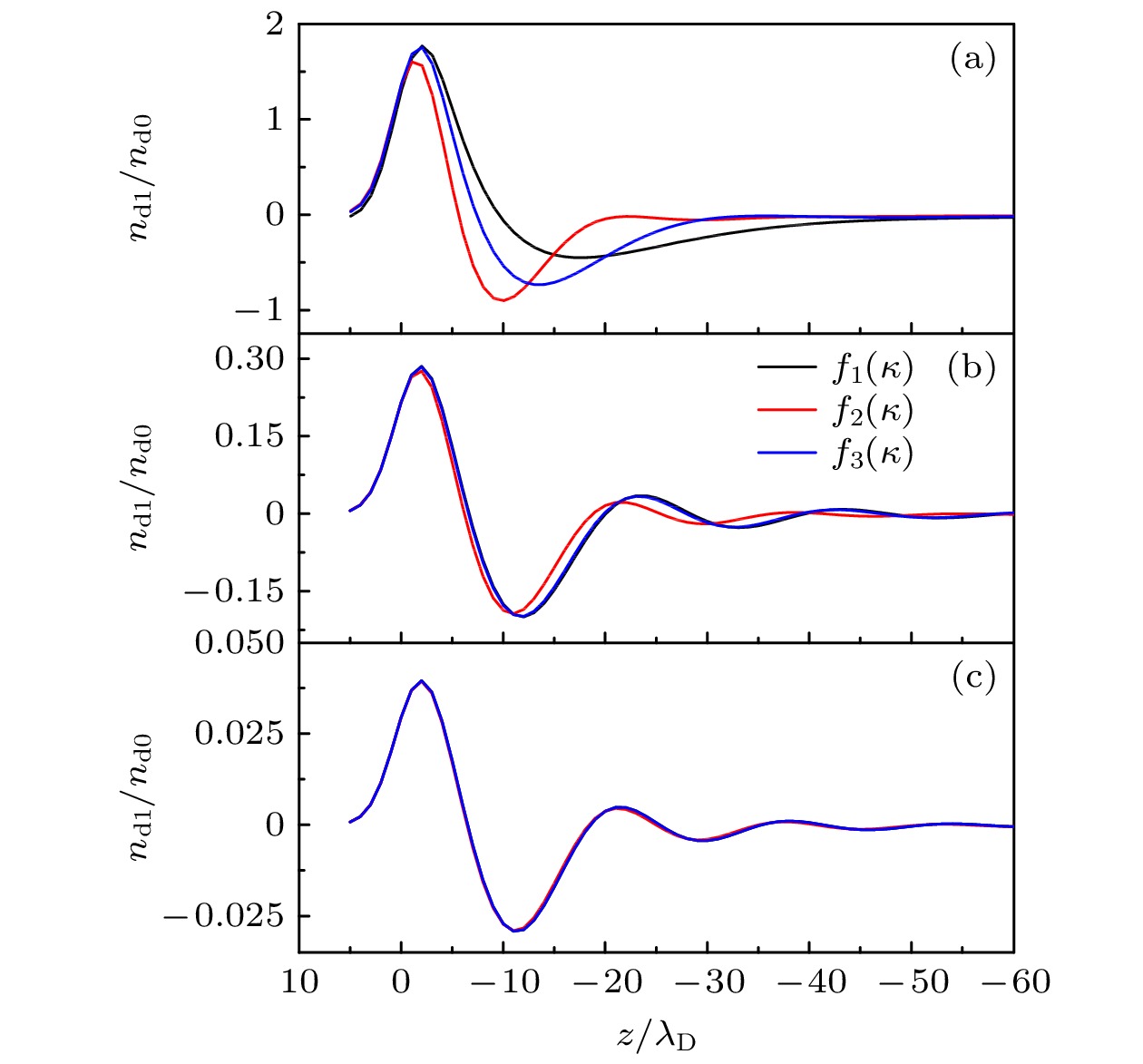
图 1 假设$ {{\boldsymbol{F}}}_{{\mathrm{L}}}/ /{{\boldsymbol{v}}}_{{\mathrm{L}}} $时, ${Z_{\text{d}}} = 4000 e$, ${n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$, 屏蔽参数分别为(a) $\kappa = 2$, (b) $\kappa = 1$和(c) $\kappa = 0.5$, 耦合参数形式分别为${f_1}(\kappa )$, ${f_2}(\kappa )$, ${f_3}(\kappa )$, 尘埃粒子扰动密度${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d0}}}}}}} \right. } {{n_{{\text{d0}}}}}}$(用${n_{{\text{d0}}}}$无量纲)随着z轴的变化情况, 其中$ x = 0 $, $ y = 0 $
Figure 1. The laser-induced perturbed density ${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d}}0}}}}} \right. } {{n_{{\text{d}}0}}}}$dependent on the axial position z, for different screening parameters: (a) $\kappa = 2$; (b) $\kappa = 1$; and (c) $\kappa = 0.5$, and different coupling parameters:${f_1}(\kappa )$, ${f_2}(\kappa )$, and ${f_3}(\kappa )$, with ${Z_{\text{d}}} = 4000 e, {\text{ }}{n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$, and $ {{\boldsymbol{F}}}_{{\mathrm{L}}}/ / {{\boldsymbol{v}}}_{{\mathrm{L}}} $.
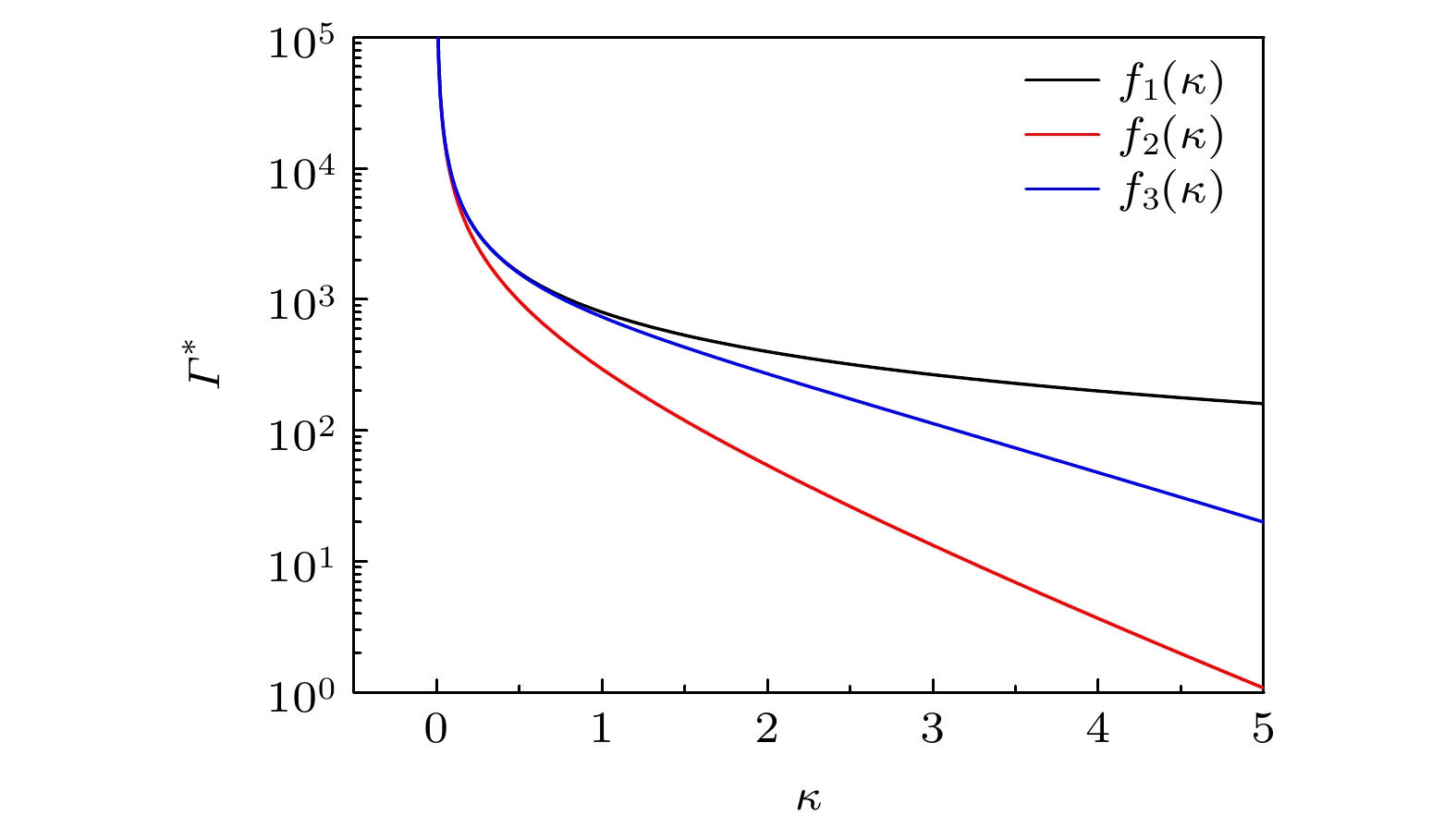
图 2 假设$ {{\boldsymbol{F}}}_{{\mathrm{L}}}/ / {{\boldsymbol{v}}}_{{\mathrm{L}}} $时, ${Z_{\text{d}}} = 4000 e$, ${n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$, 三种形式${f_1}(\kappa )$, ${f_2}(\kappa )$, ${f_3}(\kappa )$条件下, 耦合参数${\varGamma ^ * }$随着屏蔽参数$\kappa $的变化曲线
Figure 2. The coupling parameter ${\varGamma ^ * }$ change versus the screening parameter $\kappa $for the three forms ${f_1}(\kappa )$, ${f_2}(\kappa )$, ${f_3}(\kappa )$, with ${Z_{\text{d}}} = 4000 e, {\text{ }}{n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$, and $ {{\boldsymbol{F}}}_{\text{L}}/ / {{\boldsymbol{v}}}_{\text{L}} $.
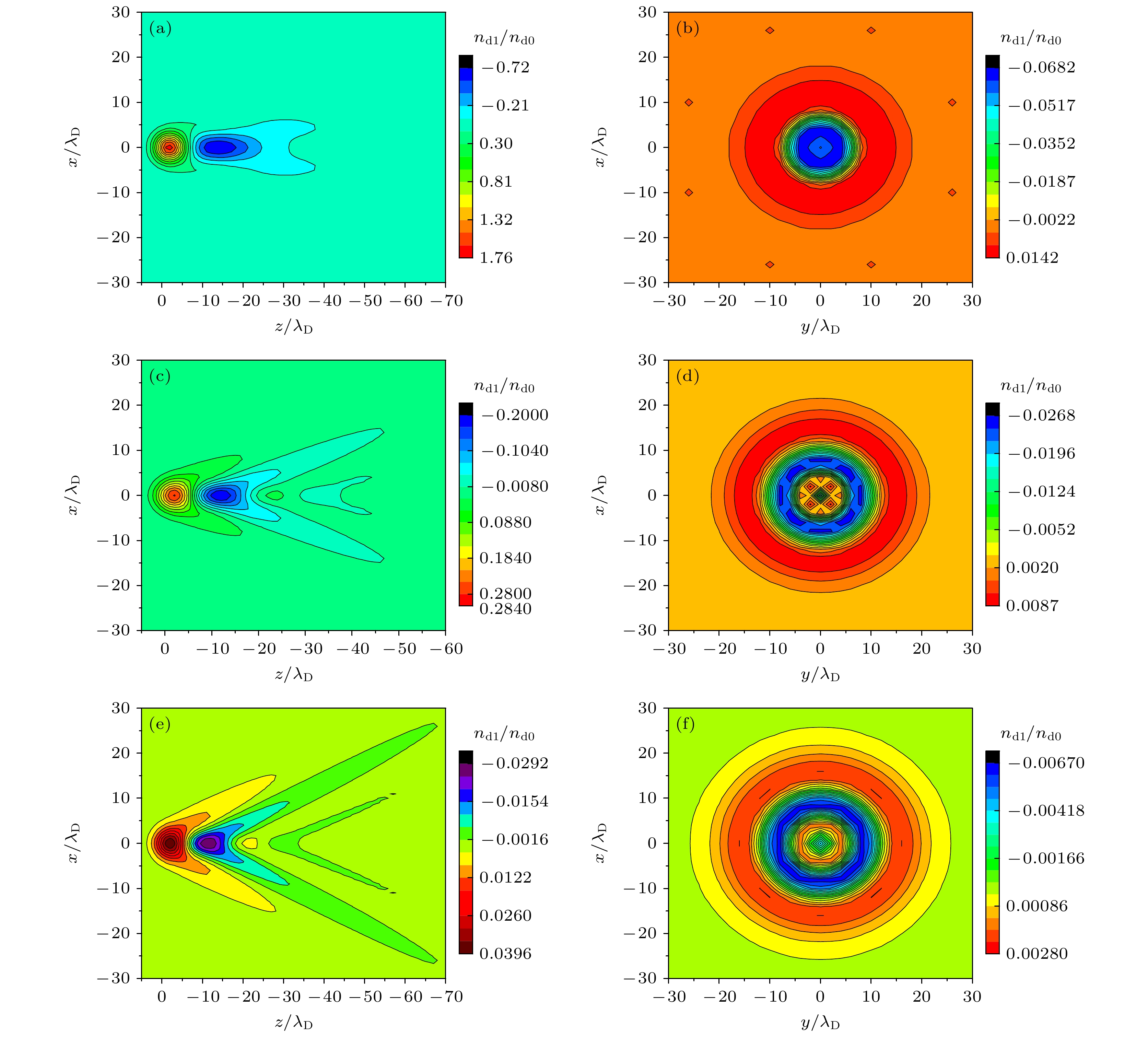
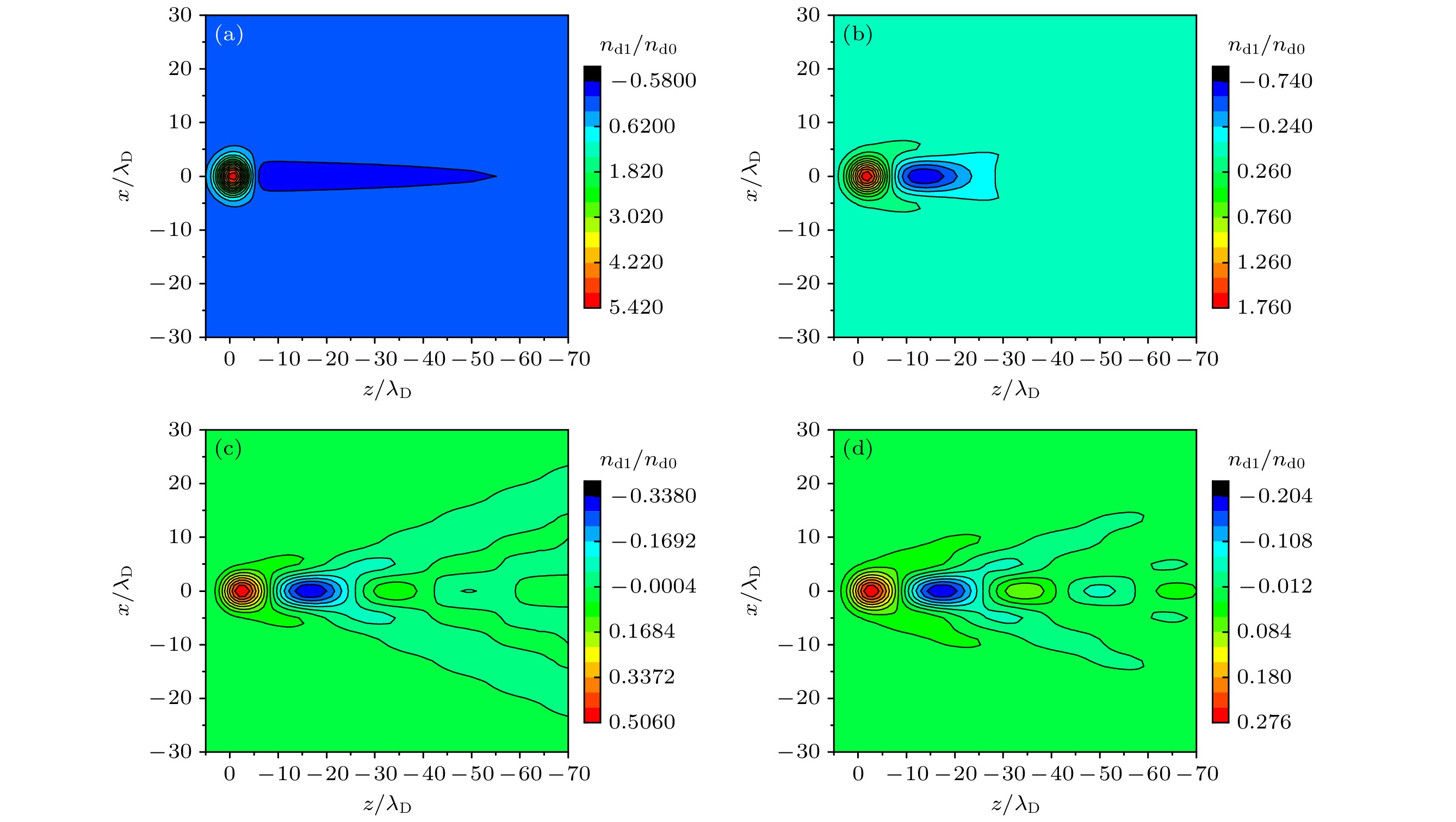
图 3 假设$ {{\boldsymbol{F}}}_{\text{L}}/ /{{\boldsymbol{v}}}_{\text{L}} $时, 在${Z_{\text{d}}} = 4000 e$, ${n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$条件下, 尘埃粒子扰动密度${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d}}0}}}}} \right. } {{n_{{\text{d}}0}}}}$(用${n_{{\text{d0}}}}$无量纲) (a), (c), (e) x-z平面(y = 0) 形成的马赫锥; (b), (d), (f) x-y截面(z = –30)形成的三维对称结构. 其中屏蔽参数分别为(a), (b) $\kappa = 2$, (c), (d) $\kappa = 1$和(e), (f) $\kappa = 0.5$
Figure 3. Mach cones by the laser-induced perturbed density ${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d}}0}}}}} \right. } {{n_{{\text{d}}0}}}}$in the (a), (c) (e) x-z plane (y = 0) and (b), (d), (f) plane x-y (z = –30), for different screening parameters (a), (b) $\kappa = 2$, (c), (d) $\kappa = 1$, and (e), (f) $\kappa = 0.5$, with ${Z_{\text{d}}} = 4000 e, {\text{ }}{n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{{{ - 3}}}}$, and $ {{\boldsymbol{F}}}_{\text{L}}/ / {{\boldsymbol{v}}}_{\text{L}} $.
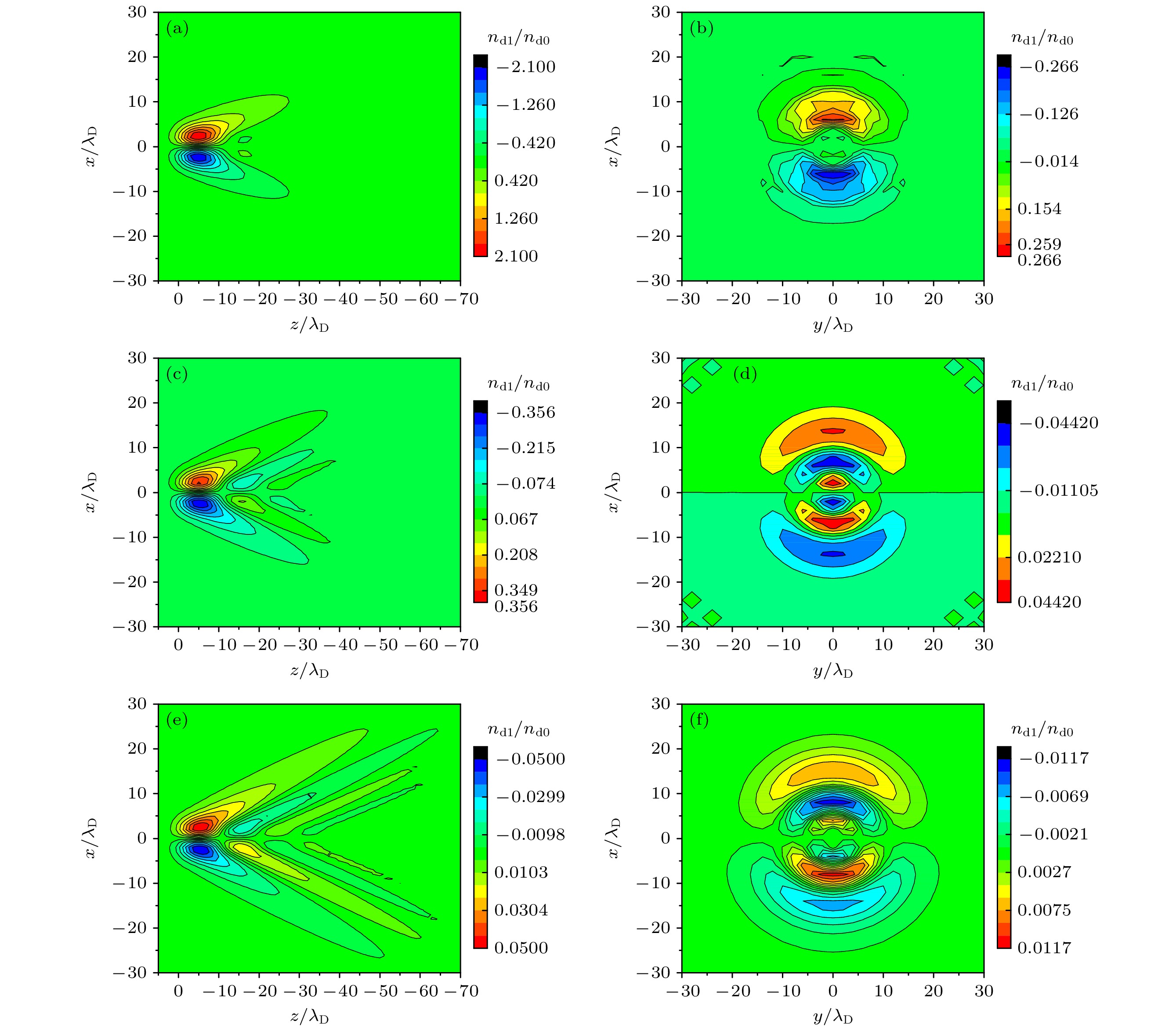
图 4 当${{\boldsymbol{F}}_{\mathrm{L}}} \bot {{\boldsymbol{v}}_{\text{L}}}$时, 在${Z_{\text{d}}} = 4000 e$, ${n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$条件下, 尘埃粒子扰动密度${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d0}}}}}}} \right. } {{n_{{\text{d0}}}}}}$(用${n_{{\text{d}}0}}$无量纲)在(a), (c), (e) x-z平面(y = 0) 形成的马赫锥, 以及在(b), (d), (f) x-y截面(z = –30)形成的三维结构, 屏蔽参数分别为 (a), (b) $\kappa = 2$, (c), (d) $\kappa = 1$和 (e), (f) $\kappa = 0.5$
Figure 4. Mach cones by the laser-induced perturbed density ${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d0}}}}}}} \right. } {{n_{{\text{d0}}}}}}$ in the (a), (c), (e) x-z plane (y = 0) and (b), (d), (f) plane x-y (z = –30), for different screening parameters (a), (b) $\kappa = 2$, (c), (d) $\kappa = 1$, and (e), (f) $\kappa = 0.5$, with ${Z_{\text{d}}} = 4000 e, $$ {\text{ }}{n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$, and ${{\boldsymbol{F}}_{\text{L}}} \bot {{\boldsymbol{v}}_{\text{L}}}$
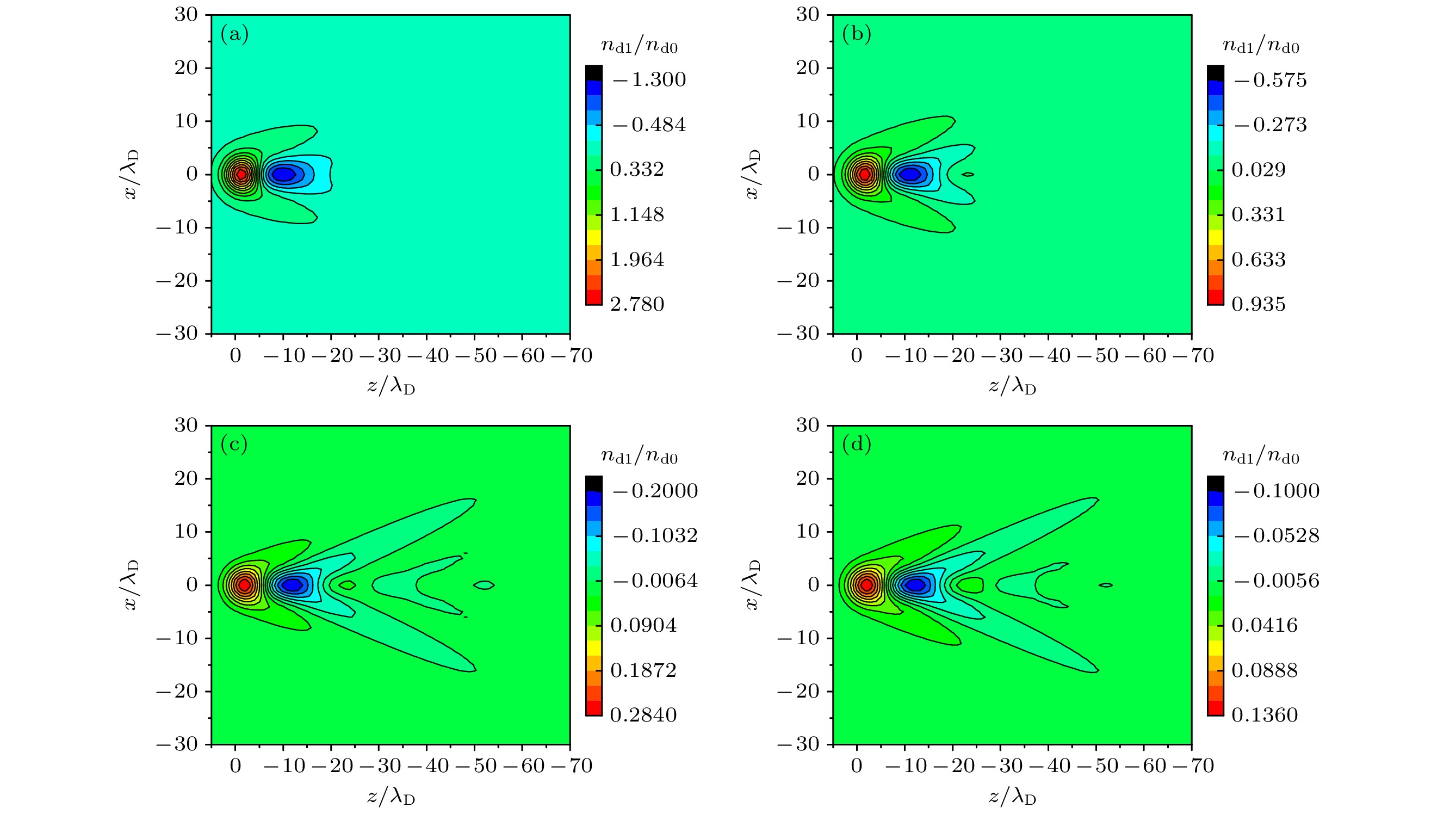
图 5 当$ {{\boldsymbol{F}}}_{\text{L}}/ / {{\boldsymbol{v}}}_{{\mathrm{L}}} $时, 在$\kappa = 1, {\text{ }}{n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$条件下, 激光诱导尘埃粒子扰动密度${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d}}0}}}}} \right. } {{n_{{\text{d}}0}}}}$(用${n_{{\text{d}}0}}$无量纲)在x-z平面($ y = 0 $)上形成的马赫锥, 尘埃表面电荷量分别为 (a) ${Z_{\text{d}}} = 1000 e$; (b) ${Z_{\text{d}}} = 2000 e$; (c) ${Z_{\text{d}}} = 4000 e$; (d) ${Z_{\text{d}}} = 6000 e$
Figure 5. Mach cones by the laser-induced perturbed density ${{{n_{{\text{d}}1}}} \mathord{\left/ {\vphantom {{{n_{{\text{d}}1}}} {{n_{{\text{d}}0}}}}} \right. } {{n_{{\text{d}}0}}}}$in the x-z plane ($ y = 0 $), for different charge on each dust particle: (a) ${Z_{\text{d}}} = 1000 e$; (b) $ {Z_{\text{d}}} = 2000 e $; (c) ${Z_{\text{d}}} = 4000 e$; (d) ${Z_{\text{d}}} = 6000 e$, with $\kappa = 1, {\text{ }}{n_{\text{e}}} = {10^9}{\kern 1 pt} {\text{c}}{{\text{m}}^{ - 3}}$, and $ {{\boldsymbol{F}}}_{\text{L}}/ / {{\boldsymbol{v}}}_{\text{L}} $.
图 6 当$ {{\boldsymbol{F}}}_{{\mathrm{L}}}/ / {{\boldsymbol{v}}}_{{\mathrm{L}}} $时, 在$\kappa = 2, {\text{ }}{Z_{\text{d}}} = 4000 e$条件下, 激光诱导尘埃粒子扰动密度${{{n_{{\text{d1}}}}} \mathord{\left/ {\vphantom {{{n_{{\text{d1}}}}} {{n_{{\text{d}}0}}}}} \right. } {{n_{{\text{d}}0}}}}$(用${n_{{\text{d0}}}}$无量纲)在x-z平面($ y = 0 $)上形成的马赫锥, 等离子体密度分别为 (a) ${n_{\text{e}}} = {10^8}\;{\text{c}}{{\text{m}}^{{{ - 3}}}}$; (b) ${n_{\text{e}}} = {10^{9}}\;{\text{c}}{{\text{m}}^{ - 3}}$; (c) ${n_{\text{e}}} = 5 \times {10^9}\;{\text{c}}{{\text{m}}^{ - 3}}$; (d) ${n_{\text{e}}} = {10^{10}}\;{\text{c}}{{\text{m}}^{ - 3}}$
Figure 6. Mach cones by the laser-induced perturbed density ${{{n_{{\text{d1}}}}} \mathord{\left/ {\vphantom {{{n_{{\text{d1}}}}} {{n_{{\text{d0}}}}}}} \right. } {{n_{{\text{d0}}}}}}$in the x-z plane ($ y = 0 $), for different plasma densities: (a) ${n_{\text{e}}} = {10^8}\;{\text{c}}{{\text{m}}^{ - 3}}$; (b) ${n_{\text{e}}} = {10^9}\;{\text{c}}{{\text{m}}^{ - 3}}$; (c) ${n_{\text{e}}} = 5 \times {10^9}\;{\text{c}}{{\text{m}}^{ - 3}}$; (d) ${n_{\text{e}}} = {10^{10}}\;{\text{c}}{{\text{m}}^{ - 3}}$, with $\kappa = 2, {\text{ }}{Z_{\text{d}}} = 4000 e$, and $ {{\boldsymbol{F}}}_{\text{L}}/ /{{\boldsymbol{v}}}_{\text{L}} $.
-
[1] Selwyn G S, Singh J, Bennett R S 1989 J. Vac. Sci. Technol. , A 7 2758
Google Scholar
[2] Fortov V E, Khrapak A G, Khrapak S A, Molotkov V I, Petrov O F 2004 Phys. Usp. 47 447
Google Scholar
[3] Merlino R L, Goree J A 2004 Phys. Today 57 32
Google Scholar
[4] Markus H T, Hubertus M T, Christina A K, Andre M, Uwe K 2023 npj Microgravity 9 13
Google Scholar
[5] Zaehringer E, Schwabe M, Zhdanov S, Mohr D P, Knapek C A, Huber P, Semenov I L, Thomas H M 2018 Phys. Plasmas 25 033703
Google Scholar
[6] Samsonov D, Goree J, Ma Z W, Bhattacharjee A, Thomas H M, Morfill G E 1999 Phys. Rev. Lett. 83 3649
Google Scholar
[7] Ma Z W, Bhattacharjee A 2002 Phys. Plasmas 9 3349
Google Scholar
[8] Melzer A, Nunomura S, Samsonov D, Ma Z W, Goree J 2000 Phys. Rev. E 62 4162
Google Scholar
[9] Sato N, Uchida G, Kaneko T, Shimizu S, Iizuka S 2001 Phys. Plasmas 8 1786
Google Scholar
[10] Cheung F, Samarian A, James B 2003 New J. Phys. 5 75
Google Scholar
[11] Schwabe M, Jiang K, Zhdanov S, Hagl T, Huber P, Ivlev A V, Lipaev A M, Molotkov V I, Naumkin V N, Sutterlin K R, Thomas H M, Fortov V E, Morfill G E, Skvortsov A, Volkov S 2011 EPL 96 55001
Google Scholar
[12] Nosenko V, Goree J, Ma Z W, Piel A 2002 Phys. Rev. Lett. 88 135001
Google Scholar
[13] Nosenko V, Goree J, Ma Z W, Dubin D H E, Piel A 2003 Phys. Rev. E 68 056409
Google Scholar
[14] Hou L J, Wang Y N, Mišković Z L 2004 Phys. Rev. E 70 056406
Google Scholar
[15] 段蒙悦, 贾文柱, 张莹莹, 张逸凡, 宋远红 2023 72 165202
Google Scholar
Duan M Y, Jia W Z, Zhang Y Y, Zhang Y F, Song Y H 2023 Acta Phys. Sin. 72 165202
Google Scholar
[16] Jia W Z, Zhang Q Z, Wang X F, Song Y H, Zhang Y Y, Wang Y N 2019 J. Phys. D: Appl. Phys. 52 015206
Google Scholar
[17] Jiang K, Hou L J, Wang Y N 2005 Chin. Phys. Lett. 22 1713
Google Scholar
[18] Hou L J, Mišković Z L, Jiang K, Wang Y N 2006 Phys. Rev. Lett. 96 255005
Google Scholar
[19] Jiang K, Hou L J, Wang Y N, Mišković Z L 2006 Phys. Rev. E. 73 016404
Google Scholar
[20] Slattery W L, Doolen G D, DeWitt H E 1980 Phys. Rev. A 21 2087
Google Scholar
[21] Ichimaru S 1982 Rev. Mod. Phys. 54 1017
Google Scholar
[22] Hartmann P, Kalman G J, Donkó Z, Kutasi K 2005 Phys. Rev. E 72 026409
Google Scholar
[23] Vaulina O S, Khrapak S A, Morfill G 2002 Phys. Rev. E 66 016404
Google Scholar
[24] Wani R, Mir A, Batool F, Tiwari S 2022 Sci. Rep. 12 11557
Google Scholar
[25] Kaw P K, Sen A 1998 Phys. Plasmas 5 3552
Google Scholar
[26] Kalman G J, Rosenberg M, DeWitt H E 2000 Phys. Rev. Lett. 84 6030
Google Scholar
[27] Ikezi H 1986 Phys. Fluids 29 1764
Google Scholar
[28] Dasgupta C, Maitra S 2021 Phys. Plasmas 28 043703
Google Scholar
[29] Bandyopadhyay P, Dey R, Kadyan S, Sen A 2014 Phys. Plasmas 21 103707
Google Scholar
[30] Nunomura S, Zhdanov S, Samsonov D, Morfill G 2005 Phys. Rev. Lett. 94 045001
Google Scholar
[31] Vaulina O S, Vladimirov S V 2002 Phys. Plasmas 9 835
Google Scholar
[32] Fortov V E, Vaulina O S, Petrov O F, Molotkov V I, Lipaev A M, Torchinsky V M, Thomas H M, Morfill G E, Khrapak S A, Semenov Yu P, Ivanov A I, Krikalev S K, Kalery A Yu, Zaletin S V, Gidzenko Yu P 2003 Phys. Rev. Lett. 90 245005
Google Scholar
[33] Caliebe D, Arp O, Piel A 2011 Phys. Plasmas 18 073702
Google Scholar
[34] Vaulina O S, Khrapak S A 2000 J. Exp. Theor. Phys. 90 287
Google Scholar
[35] Hamaguchi S, Farouki R T, Dubin D H E 1997 Phys. Rev. E 56 4671
Google Scholar
[36] Epstein P S 1924 Phys. Rev. 23 710
Google Scholar
[37] Slattery W L, Doolen G D, DeWitt H E 1982 Phys. Rev. A 26 2255
Google Scholar
[38] Dubin D 2000 Phys. Plasmas 7 3895
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1816
- PDF Downloads: 79
- Cited By: 0
