-
The line defect of graphene has significant applications in valleytronics, which has received extensive attention in recent years. It is found experimentally that there exists local deformation around the line defect. Current studies generally believe that the influence of local deformation on the valley transport properties can be negligible, because the modifications to the nearest neighbour hopping energy is less than 5% under the small deformation. Based on the first-principles calculations and the non-equilibrium Green’s function method, we investigated the effect of local deformation on the valley transport properties of two different kinds of line defects, the 58 ring line defect and the 57 ring line defect. It is found that for the 58 ring line defect, the effect of local deformation on the valley transmission coefficient is not evident at lower energies. However, at higher energies, the impact of local deformation is obvious, and the maximum valley transmission coefficient does not decrease with increasing energy, but can be maintained 1 within a large energy range. In contrast, the influence of local deformation on the valley transmission coefficient of the 57 ring line defect indeed can be negligible, regardless of the level of energy. Further investigation indicates that the change of the C—C bond length connected to the two defect atoms in the 58 ring plays a key role in the transmission of the valley states across the line defect. If this part of the influence is not taken into account, the valley transmission coefficient is nearly unaffected by the local deformation. The valley state enters the right side of the line defect directly through the bond connected to the line defect, so the change in bond length connected to the line defect has a significant impact on the valley transmission. This special structure does not exist in the 57 ring, where the valley states will have to pass through a narrow region containing 57 ring to enter the right side of the line defect, resulting in different valley scattering phenomena. By constructing two parallel line defects, the 100% valley polarization can be achieved in a large angular range with the 58 ring line defect. The finding has important implications for the design of graphene line defect based valley filters.
-
Keywords:
- graphene /
- line defect /
- first-principles calculations /
- local deformation /
- valley filter
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] 廖天军, 杨智敏, 林比宏 2021 70 227901
Google Scholar
Liao T J, Yang Z M, Lin B H 2021 Acta Phys. Sin. 70 227901
Google Scholar
[3] Avouris P, Chen Z, Perebeinos V 2007 Nat. Nanotechnol. 2 605
Google Scholar
[4] Geim A, Novoselov K S 2007 Nat. Mater. 6 183
Google Scholar
[5] Rycerz A, Tworzydlo J, Beenakker C 2007 Nat. Phys. 3 172
Google Scholar
[6] Enoki T, Ando T 2020 Physics and Chemistry of Graphene (Graphene to Nanographene) (2nd Ed.) (Singapore: Jenny Stanford Publishing)
[7] 邓富胜, 孙勇, 刘艳红, 董丽娟, 石云龙 2017 66 144204
Google Scholar
Deng F S, Sun Y, Liu Y H, Dong L J, Shi Y L 2017 Acta Phys. Sin. 66 144204
Google Scholar
[8] Fujita T, Jalil M B A, Tan S G 2010 Appl. Phys. Lett. 97 043508
Google Scholar
[9] Wang S K, Tian H Y, Sun M L 2023 J. Phys.: Condens. Matter 35 304002
Google Scholar
[10] Recher P, Nilsson J, Burkard G, Trauzettel B 2009 Phys. Rev. B 79 085407
Google Scholar
[11] Sekera T, Bruder C, Mele E J, Tiwari R P 2017 Phys. Rev. B 95 205431
Google Scholar
[12] Golub L E, Tarasenko S A, Entin M V, Magarill L I 2011 Phys. Rev. B 84 195408
Google Scholar
[13] Kelardeh H K, Saalmann U, Rost Jan M 2022 Phys. Rev. Res. 4 L022014
Google Scholar
[14] Wang S, Pratama F R, Ukhtary M S 2020 Phys. Rev. B 101 081414(R
Google Scholar
[15] Yazyev O V, Chen Y P 2014 Nat. Nanotechnol. 9 755
Google Scholar
[16] Huang P Y, Ruiz-Vargas C S, van der Zande A M, Whitney W S, Levendorf M P, Kevek J W, Garg S, Alden J S, Hustedt C J, Zhu Y, Park J, McEuen P L, Muller D A 2011 Nature 469 389
Google Scholar
[17] Komsa H P, Krasheninnikov A 2017 Adv. Electron. Mater. 3 1600468
Google Scholar
[18] Lahiri J, Lin Y, Bozkurt P, Oleynik Ivan I, Batzill M 2010 Nat. Nanotechnol. 5 326
Google Scholar
[19] Jolie W, Murray C, Weiß P S, et al. 2019 Phys. Rev. X 9 011055
Google Scholar
[20] Lasek K, Li J F, Kolekar S, et al. 2021 Surf. Sci. Rep. 76 100523
Google Scholar
[21] Tian H Y, Ren C D, Wang S K 2022 Nanotechnology 33 212001
Google Scholar
[22] Gunlycke D, White C T 2011 Phys. Rev. Lett. 106 136806
Google Scholar
[23] Pulkin A, Yazyev O V 2016 Phys. Rev. B 93 041419
Google Scholar
[24] Chen J H, Autes G, Alem N, Gargiulo F, Gautam A, Linck M, Kisielowski C, Yazyev O V, Louie S G, Zettl A 2014 Phys. Rev. B 89 121407(R
Google Scholar
[25] Liu Y, Song J, Li Y, Liu Y, Sun Q F 2013 Phys. Rev. B 87 195445
Google Scholar
[26] Ren C D, Lu W T, Zhou B H, Li Y F, Li D Y, Wang S K, Tian H Y 2020 J. Phys.: Condens. Matter 32 365302
Google Scholar
[27] Du L, Ren C D, Cui L, Lu W T, Tian H Y, Wang S K 2022 Phys. Scr. 97 125825
Google Scholar
[28] Jiang L W, Lü X L, Zheng Y S 2011 Phys. Lett. A 376 136
Google Scholar
[29] Pereira V M, Castro Neto A H, Peres N M R 2009 Phys. Rev. B 80 045401
Google Scholar
[30] Wang S, Hung N T, Tian H, Islam M S, Saito R 2021 Phys. Rev. Appl. 16 024030
Google Scholar
[31] Kresse G, Hafner J 1993 Phys. Rev. B 47 558(R
Google Scholar
[32] Perdew J P, Burke K. Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[33] Hao Y F, Wang L, Liu Y Y, Chen H, Wang X H, Tan C, Nie S, Suk J W, Jiang T F, Liang T F, Xiao J F, Ye W J, Dean C R, Yakobson B I, McCarty K F, Kim P, Hone J, Colombo L, Ruoff R S 2016 Nat. Nanotechnol. 11 426
Google Scholar
[34] Bharathi M S, Hao Y F, Ramanarayan H, Rywkin S, Hone J, Colombo L, Ruoff R S, Zhang Y W 2018 ACS Nano 12 9372
Google Scholar
-
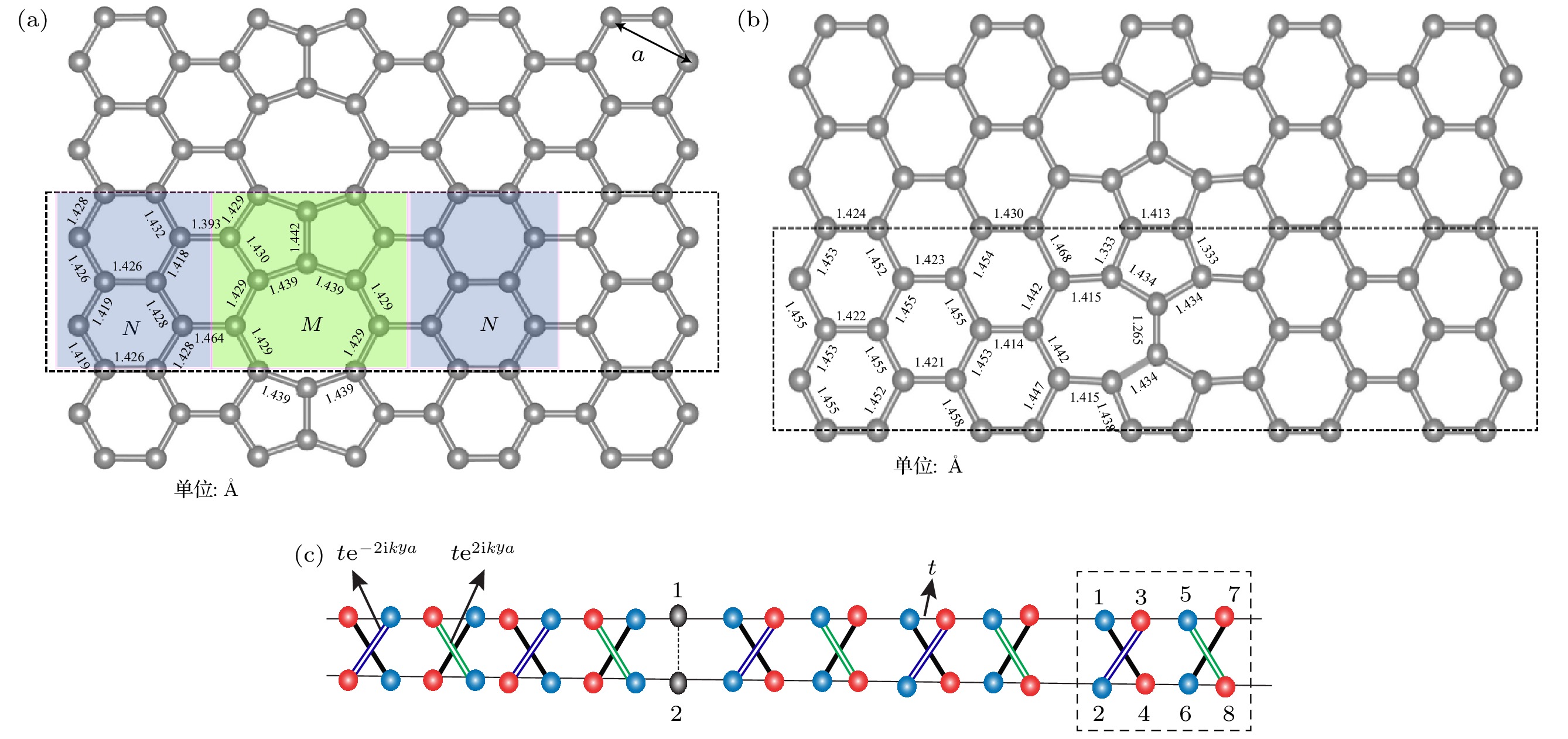
图 1 (a)石墨烯58环线缺陷结构示意图, M和N分别表示离线缺陷最近邻和次近邻形变区域. (b)石墨烯57环线缺陷结构示意图, 两条虚线之间区域是最小周期性单元, 图中C—C键长是通过第一性原理计算得到的, 线缺陷左右两侧键长关于对称轴对称. (c)无限大石墨烯58环线缺陷简化晶格模型, 虚线框表示一个超胞
Figure 1. (a) Diagrammatic sketch for the 58 ring line defect of graphene, where M and N represent the nearest neighbor and next nearest neighbor deformation regions away from the line defect, respectively. (b) Diagrammatic sketch for the 57 ring line defect of graphene. The region between two neighbouring dotted lines is a unit cell. The C—C bond lengths were calculated using first-principles theory, they are symmetric with respect to the symmetry axis. (c) The simplified lattice model of the infinite graphene with 58 ring line defect, and the dashed box denotes a supercell
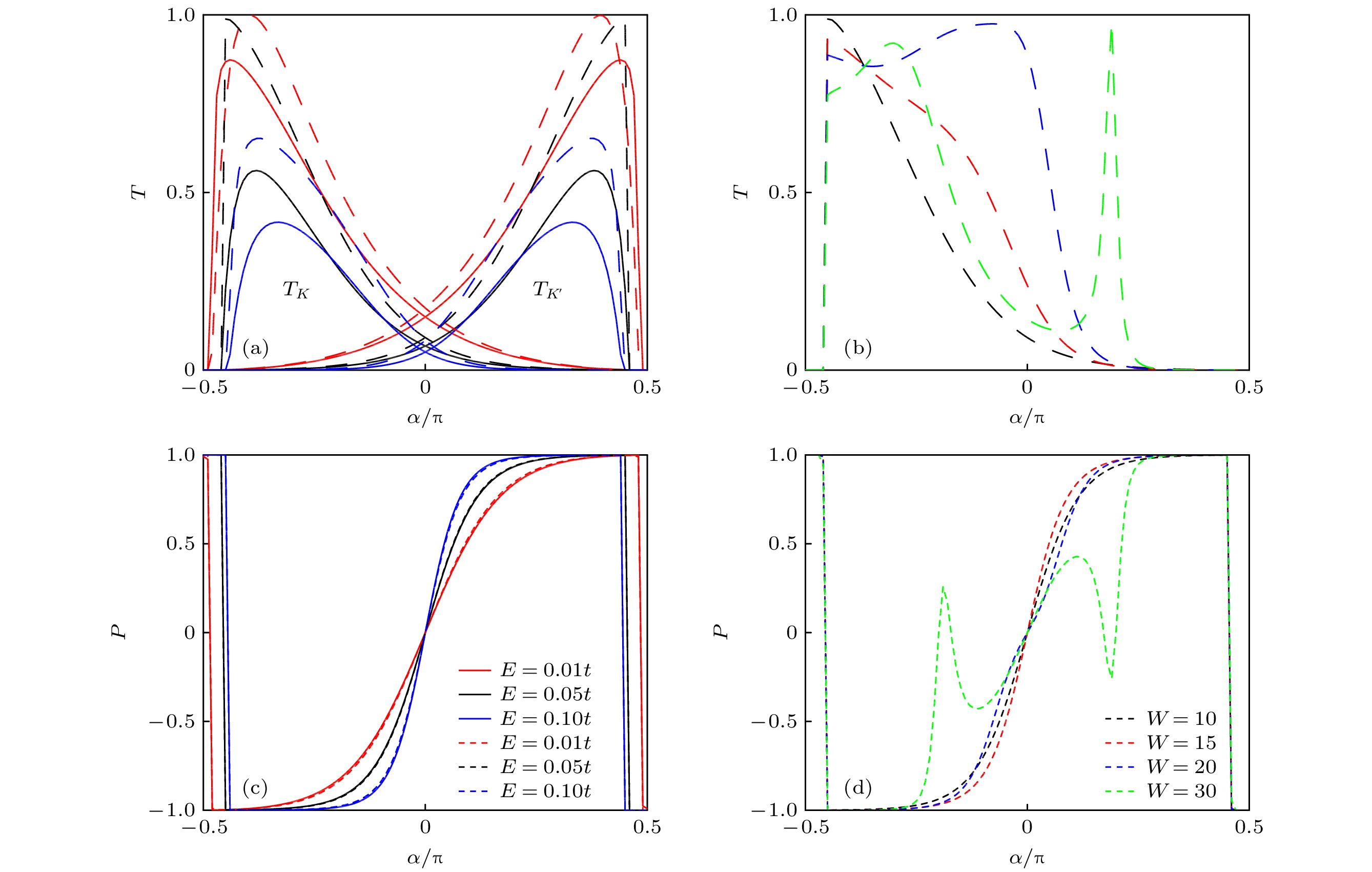
图 2 不同费米能下K谷隧穿系数
$T_K$ 随散射角α变化关系 (a)未考虑局域形变的影响; (b)考虑局域形变的影响. 右上角插图$T_{\rm{M}}$ ,$T_{\rm{N}}$ 和$T_{{\rm{MN}}}$ 分别表示$E=0.1 t$ 时只考虑图1(a)中M区域, N区域以及MN区域形变的结果Figure 2. Transmission coefficient
$T_K$ as a function of α for different Fermi energies: (a) Local deformations are not taken into account; (b) local deformations are taken into account. In the inset,$T_{\rm{M}}$ ,$T_{\rm{N}}$ and$T_{{\rm{MN}}}$ respectively represent the results of considering only the deformation in the M region, the N region and MN regions in Fig. 1(a) when$E=0.1 t$ 
图 3 (a), (c)存在两个平行线缺陷时, 不同费米能下
$K/K'$ 谷隧穿系数$T_{K/K'}$ 以及谷极化度P随散射角α变化关系; (b), (d)存在两个平行线缺陷时, 线缺陷之间距离W不同时$T_{K}$ 以及谷极化度P随散射角α的变化关系. 其中(a), (c)中两个线缺陷之间的距离为$W=10$ , (b), (d)中费米能为$E=0.05 t$ . 虚线/实线表示考虑/未考虑局域形变影响的结果. 两个线缺陷之间的距离W以$\sqrt{3}a$ 为单位Figure 3. (a), (c) Transmission coefficients
$T_{K/K'}$ and the valley polarization P as a function of α for different Fermi energies in the presence of two parallel line defects; (b), (d) transmission coefficients$T_{K}$ and the valley polarization P as a function of α for different width between the two line defects in the presence of two parallel line defects. The width between two line defects in panels (a) and (c) is$W=10$ and the Fermi energy in panels (b) and (d) is$E=0.05 t$ . Dotted/solid lines correspond to the results of considering/without considering the influence of local deformations. The distance between the two line defects W is in units of$\sqrt{3}a$ 
图 4 不同费米能下57环线缺陷K谷隧穿系数
$T_K$ 随散射角α变化关系 (a)未考虑局域形变的影响; (b)考虑局域形变的影响Figure 4. Transmission coefficient
$T_K$ in 57 ring line defect as a function of α for different Fermi energies: (a) Local deformations are not taken into account; (b) local deformations are taken into account -
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] 廖天军, 杨智敏, 林比宏 2021 70 227901
Google Scholar
Liao T J, Yang Z M, Lin B H 2021 Acta Phys. Sin. 70 227901
Google Scholar
[3] Avouris P, Chen Z, Perebeinos V 2007 Nat. Nanotechnol. 2 605
Google Scholar
[4] Geim A, Novoselov K S 2007 Nat. Mater. 6 183
Google Scholar
[5] Rycerz A, Tworzydlo J, Beenakker C 2007 Nat. Phys. 3 172
Google Scholar
[6] Enoki T, Ando T 2020 Physics and Chemistry of Graphene (Graphene to Nanographene) (2nd Ed.) (Singapore: Jenny Stanford Publishing)
[7] 邓富胜, 孙勇, 刘艳红, 董丽娟, 石云龙 2017 66 144204
Google Scholar
Deng F S, Sun Y, Liu Y H, Dong L J, Shi Y L 2017 Acta Phys. Sin. 66 144204
Google Scholar
[8] Fujita T, Jalil M B A, Tan S G 2010 Appl. Phys. Lett. 97 043508
Google Scholar
[9] Wang S K, Tian H Y, Sun M L 2023 J. Phys.: Condens. Matter 35 304002
Google Scholar
[10] Recher P, Nilsson J, Burkard G, Trauzettel B 2009 Phys. Rev. B 79 085407
Google Scholar
[11] Sekera T, Bruder C, Mele E J, Tiwari R P 2017 Phys. Rev. B 95 205431
Google Scholar
[12] Golub L E, Tarasenko S A, Entin M V, Magarill L I 2011 Phys. Rev. B 84 195408
Google Scholar
[13] Kelardeh H K, Saalmann U, Rost Jan M 2022 Phys. Rev. Res. 4 L022014
Google Scholar
[14] Wang S, Pratama F R, Ukhtary M S 2020 Phys. Rev. B 101 081414(R
Google Scholar
[15] Yazyev O V, Chen Y P 2014 Nat. Nanotechnol. 9 755
Google Scholar
[16] Huang P Y, Ruiz-Vargas C S, van der Zande A M, Whitney W S, Levendorf M P, Kevek J W, Garg S, Alden J S, Hustedt C J, Zhu Y, Park J, McEuen P L, Muller D A 2011 Nature 469 389
Google Scholar
[17] Komsa H P, Krasheninnikov A 2017 Adv. Electron. Mater. 3 1600468
Google Scholar
[18] Lahiri J, Lin Y, Bozkurt P, Oleynik Ivan I, Batzill M 2010 Nat. Nanotechnol. 5 326
Google Scholar
[19] Jolie W, Murray C, Weiß P S, et al. 2019 Phys. Rev. X 9 011055
Google Scholar
[20] Lasek K, Li J F, Kolekar S, et al. 2021 Surf. Sci. Rep. 76 100523
Google Scholar
[21] Tian H Y, Ren C D, Wang S K 2022 Nanotechnology 33 212001
Google Scholar
[22] Gunlycke D, White C T 2011 Phys. Rev. Lett. 106 136806
Google Scholar
[23] Pulkin A, Yazyev O V 2016 Phys. Rev. B 93 041419
Google Scholar
[24] Chen J H, Autes G, Alem N, Gargiulo F, Gautam A, Linck M, Kisielowski C, Yazyev O V, Louie S G, Zettl A 2014 Phys. Rev. B 89 121407(R
Google Scholar
[25] Liu Y, Song J, Li Y, Liu Y, Sun Q F 2013 Phys. Rev. B 87 195445
Google Scholar
[26] Ren C D, Lu W T, Zhou B H, Li Y F, Li D Y, Wang S K, Tian H Y 2020 J. Phys.: Condens. Matter 32 365302
Google Scholar
[27] Du L, Ren C D, Cui L, Lu W T, Tian H Y, Wang S K 2022 Phys. Scr. 97 125825
Google Scholar
[28] Jiang L W, Lü X L, Zheng Y S 2011 Phys. Lett. A 376 136
Google Scholar
[29] Pereira V M, Castro Neto A H, Peres N M R 2009 Phys. Rev. B 80 045401
Google Scholar
[30] Wang S, Hung N T, Tian H, Islam M S, Saito R 2021 Phys. Rev. Appl. 16 024030
Google Scholar
[31] Kresse G, Hafner J 1993 Phys. Rev. B 47 558(R
Google Scholar
[32] Perdew J P, Burke K. Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[33] Hao Y F, Wang L, Liu Y Y, Chen H, Wang X H, Tan C, Nie S, Suk J W, Jiang T F, Liang T F, Xiao J F, Ye W J, Dean C R, Yakobson B I, McCarty K F, Kim P, Hone J, Colombo L, Ruoff R S 2016 Nat. Nanotechnol. 11 426
Google Scholar
[34] Bharathi M S, Hao Y F, Ramanarayan H, Rywkin S, Hone J, Colombo L, Ruoff R S, Zhang Y W 2018 ACS Nano 12 9372
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2461
- PDF Downloads: 81
- Cited By: 0
