-
Bandgap engineering in graphene has been a hot topic in condensed matter physics. Although several line defects have been experimentally reported in graphene, the relationship between the bandgap engineering and the line defects has not yet been discussed. In this work, by combining the Green’s function method with the Landauer-Büttiker formula, we study theoretically the electron transport along disordered ZGNRs through taking into account three types of line defects which arise from random distribution of 4-8 rings. Our results show that although there exist electronic states around the Fermi energy of the disordered ZGNRs with randomly distributed line defects, all these electronic states are localized and a transmission gap appears around the Fermi energy. This localization phenomenon originates from the structural disorder induced by the randomly distributed line defects. To demonstrate the robustness of transmission gaps, we further calculate the conductance values of disordered ZGNR with different insertion probabilities and widths, finding that the size of transmission gap strongly depends upon the types of disorder, disorder degree, and width. When the disorder degree of line defects is low or the width of the nanoribbon is narrow, there is a notable difference in the size of the transmission gaps among the three types of disordered ZGNRs. As the width or disorder degree increases, the transmission gap size tends to be consistent. Like armchair ZGNRs, the transmission gap size decreases with the increase of width or disorder of ZGNR. Nonetheless, the openings of the transmission gaps in three types of disordered ZGNRs remain robust, regardless of variations in degree of disorder or width. These results are helpful in designing line-defect based nanodevices.
-
Keywords:
- graphene nanoribbons /
- quantum transport /
- line defects /
- Green’s function
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D E, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Beenakker C W J 2008 Rev. Mod. Phys. 80 1337
Google Scholar
[3] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801
Google Scholar
[4] Xu X R, Cheng S G 2013 J. Phys. Condens. Matter 25 075304
Google Scholar
[5] Huang Y L, Wang K T, Xing Y, Liu G B, Zhao H K 2019 Carbon 143 641
Google Scholar
[6] Cheng S G, Liu H, Jiang H, Sun Q F, Xie X C 2018 Phys. Rev. Lett. 121 156801
Google Scholar
[7] Wei M, Zhou M, Wang B, Xing Y 2020 Phys. Rev. B 102 075432
Google Scholar
[8] 陈兴, 赵晗, 张艳, 刘露, 杨志宏, 宋玲玲 2021 70 198503
Google Scholar
Chen X, Zhao H, Zhang Y, Liu L, Yang Z H, Song L L 2021 Acta Phys. Sin. 70 198503
Google Scholar
[9] Fu H Y, Sun F, Liu R, Suo Y Q, Bi J J, Wang C K, Li Z L 2019 Phys. Lett. A 383 867
Google Scholar
[10] Niu L L, Fu H Y, Suo Y Q, Liu R, Sun F, Wang S S, Zhang G P, Wang C K, Li Z L 2021 Physica E 128 114542
Google Scholar
[11] 刘贵立, 杨忠华 2018 67 076301
Google Scholar
Liu G L, Yang Z H, 2018 Acta Phys. Sin. 67 076301
Google Scholar
[12] 张慧珍, 李金涛, 吕文刚, 杨海方, 唐成春, 顾长志, 李俊杰 2017 66 217301
Google Scholar
Zhang H Z, Li J T, Lv W G, Yang H F, Tang C C, Gu C Z, Li J J 2017 Acta Phys. Sin. 66 217301
Google Scholar
[13] Merino Díez N, Garcia Lekue A, Carbonell Sanromà E, Li J, Corso M, Colazzo L, Sedona F, Sánchez Portal D, Pascual J I, de Oteyza D G 2017 ACS Nano 11 11661
Google Scholar
[14] Zhou M, Jin H, Xing Y 2020 Phys. Rev. Appl. 13 044006
Google Scholar
[15] Hashimoto A, Suenaga K, Gloter A, Urita K, Iijima S 2004 Nature 430 870
Google Scholar
[16] Islam A E, Susner M A, Carpena Núñez J, Back T C, Rao R, Jiang J, Pachter R, Tenney S A, Boeckl J J, Maruyama B 2020 Carbon 166 446
Google Scholar
[17] Lahiri J, Lin Y, Bozkurt P, Oleynik I I, Batzill M 2010 Nat. Nanotechnol. 5 326
Google Scholar
[18] Fei Y, Fu Y, Bai X, Du L, Li Z, Komber H, Low K H, Zhou S, Phillips D L, Feng X, Liu J 2021 J. Am. Chem. Soc. 143 2353
Google Scholar
[19] Liu M, Liu M, She L, Zha Z, Pan J, Li S, Li T, He Y, Cai Z, Wang J, Zheng Y, Qiu X, Zhong D 2017 Nat. Commun. 8 14924
Google Scholar
[20] Fan Q, Yan L, Tripp M W, Krejčí O, Dimosthenous S, Kachel S R, Chen M, Foster A S, Koert U, Liljeroth P 2021 Science 372 852
Google Scholar
[21] Gunlycke D, White C T 2011 Phys. Rev. Lett. 106 136806
Google Scholar
[22] Song J, Liu H, Jiang H, Sun Q F, Xie X C 2012 Phys. Rev. B 86 085437
Google Scholar
[23] Tong Z, Pecchia A, Yam C, Dumitrică T, Frauenheim T 2022 Adv. Energy Mater. 12 2200657
Google Scholar
[24] Kong W, Wang R, Xiao X, Zhan F, Gan L Y, Wei J, Fan J, Wu X 2021 J. Phys. Chem. Lett. 12 10874
Google Scholar
[25] Datta S 1995 Electronic Transport in Mesoscopic Systems (Cambridge: Cambridge University Press)
[26] Zhang Y T, Jiang H, Sun Q F, Xie X C 2010 Phys. Rev. B 81 165404
Google Scholar
[27] Chen L, Ouyang F, Ma S, Fang T F, Guo A M, Sun Q F, 2020 Phys. Rev. B 101 115417
Google Scholar
[28] Hu P J, Wang S X, Chen X F, Gao X H, Fang T F, Guo A M, Sun Q F 2022 Phys. Rev. Appl. 17 024074
Google Scholar
[29] Sancho M L, Sancho J L, Rubio J 1984 J. Phys. F: Met. Phys. 14 1205
Google Scholar
[30] Sancho M L, Sancho J L, Sancho J L, Rubio J 1985 J. Phys. F:Met. Phys. 15 851
Google Scholar
[31] 王雪梅, 刘红 2011 60 047102
Google Scholar
Wang X M, Liu H 2011 Acta Phys. Sin. 60 047102
Google Scholar
-
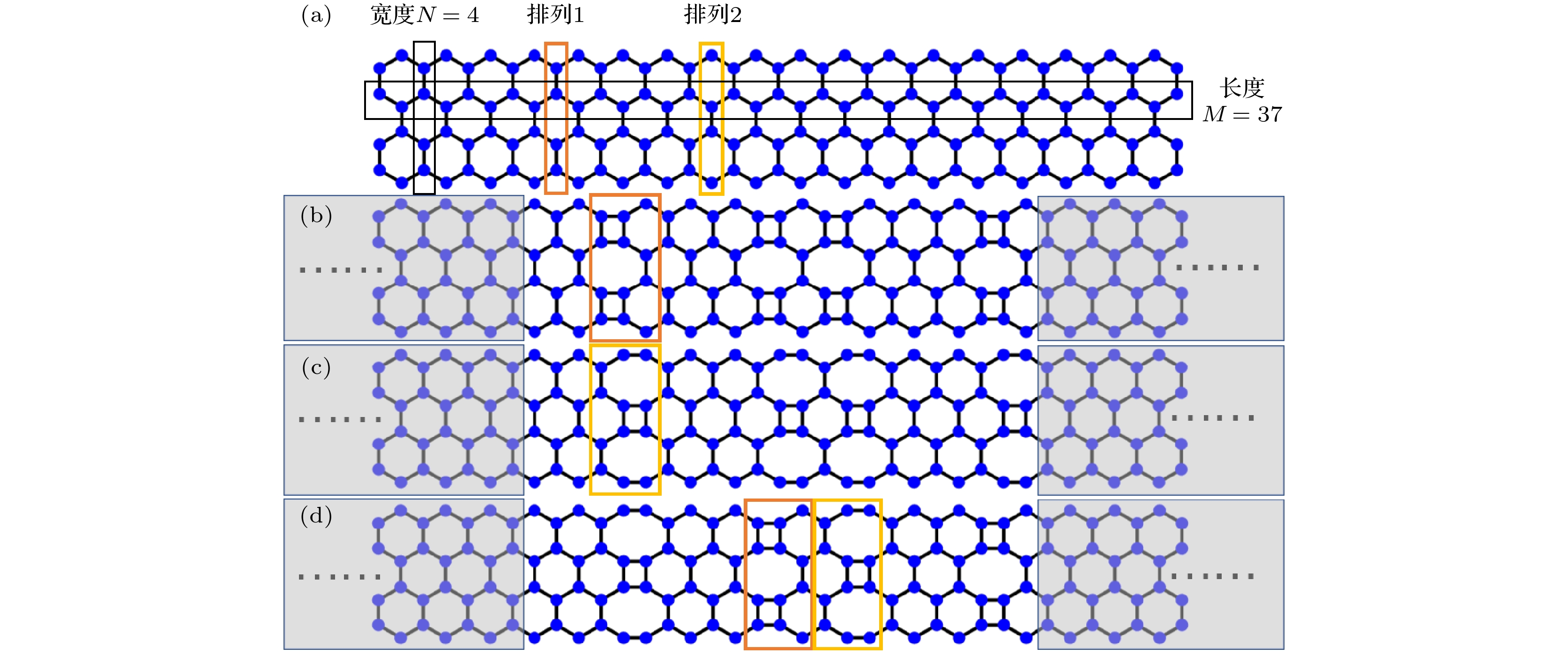
图 1 ZGNR和三类无序ZGNRs示意图 (a) ZGNR; (b), (c), (d) 第I, II和III类无序ZGNRs与左右半无限长ZGNRs耦合形成的二端体系
Figure 1. Schematic diagrams of ZGNR and three types of disordered ZGNRs: (a) ZGNR; (b), (c), (d) the two-terminal system constructed by the type I, II and III disordered ZGNRs coupled to left and right semi-infinite ZGNRs, respectively.
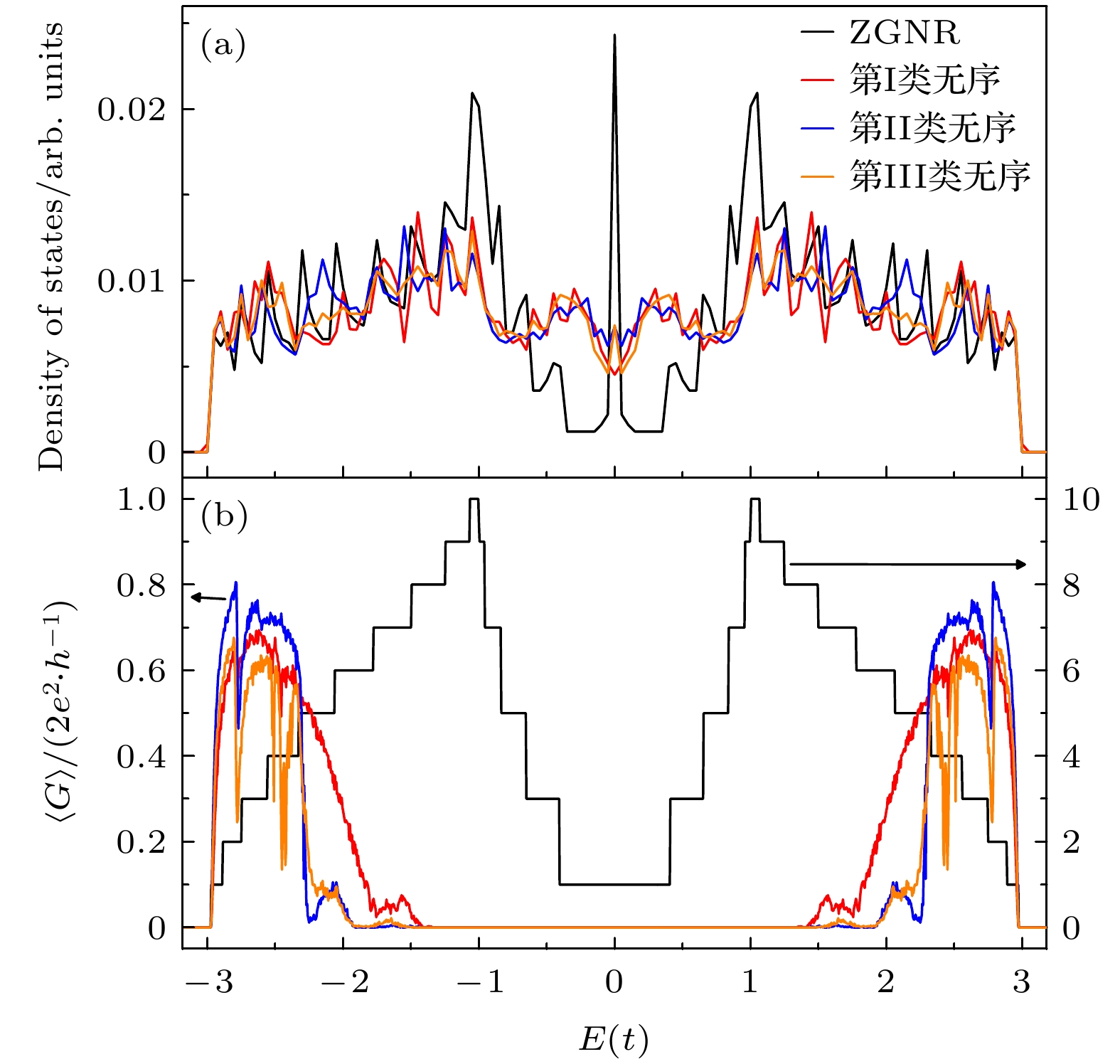
图 2 完美ZGNR和三类无序ZGNRs的电子结构和电输运性质 (a) 态密度随E的变化曲线; (b) 平均电导
$ \left\langle G \right\rangle $ 随E的变化曲线, 其中左纵坐标对应无序ZGNRs, 右纵坐标对应完美ZGNR. 对于所有ZGNRs: N =10, M = 10000Figure 2. Electronic structures and transport properties of perfect ZGNR and three types of disordered ZGNRs: (a) Density of states as a function of E for perfect ZGNR and three types of disordered ZGNRs; (b) averaged conductance
$ \left\langle G \right\rangle $ as a function of E for perfect ZGNR (right axis) and three types of disordered ZGNRs (left axis). Here, N = 10 and M = 10000 for all ZGNRs.
图 3 三类无序ZGNRs在不同概率P下的
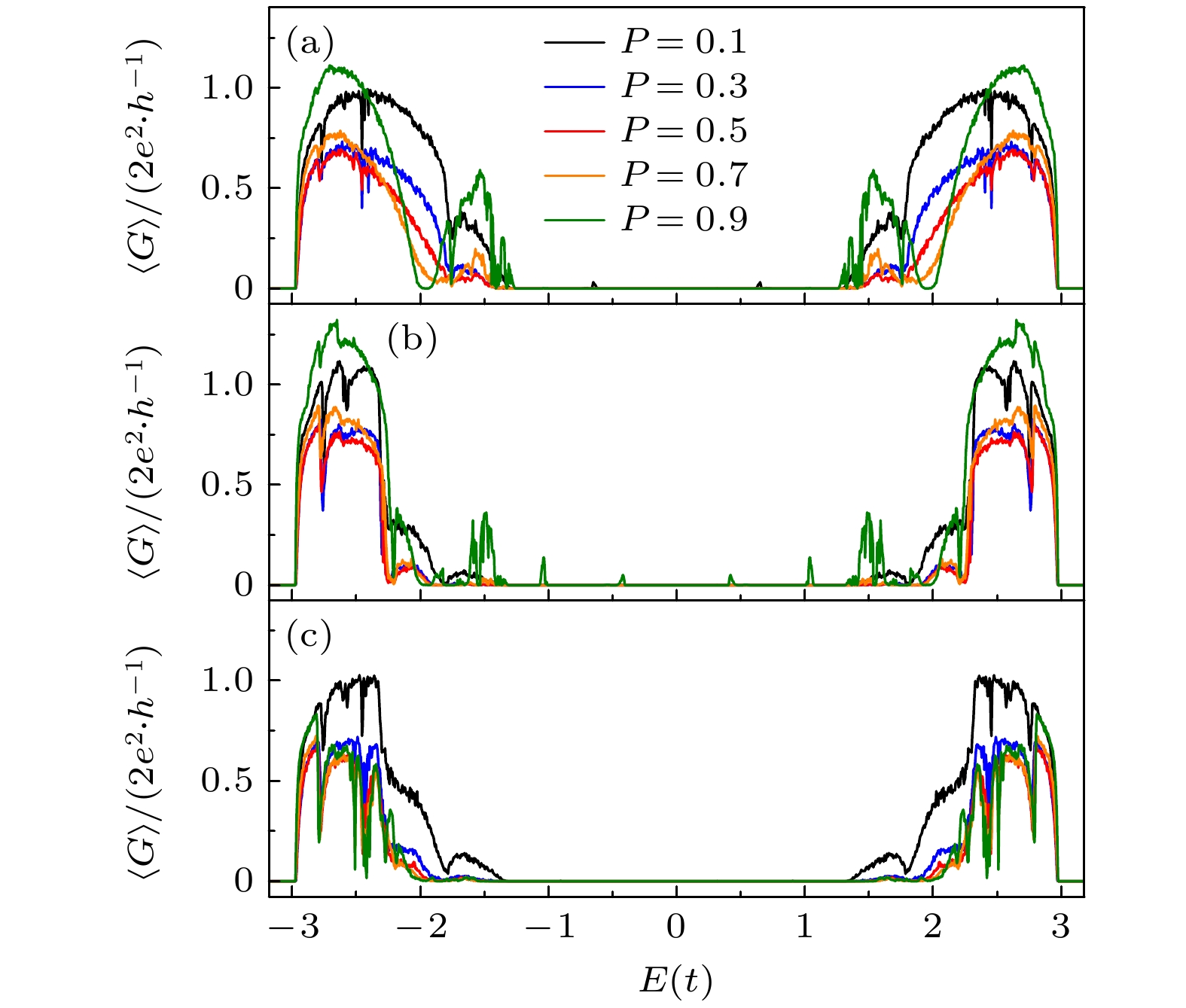
$ \left\langle G \right\rangle $ 随E的变化曲线 (a), (b), (c) 分别对应第I, II和III类无序ZGNRs. 对于所有ZGNRs: N = 10, M =10000Figure 3.
$ \left\langle G \right\rangle $ as a function of E for three types of disordered ZGNRs for different probabilities P. (a), (b) and (c) correspond to three types of disordered ZGNRs, respectively. Here, N = 10 and M = 10000 for all disordered ZGNRs.
图 4 三类无序ZGNRs在不同宽度N下的
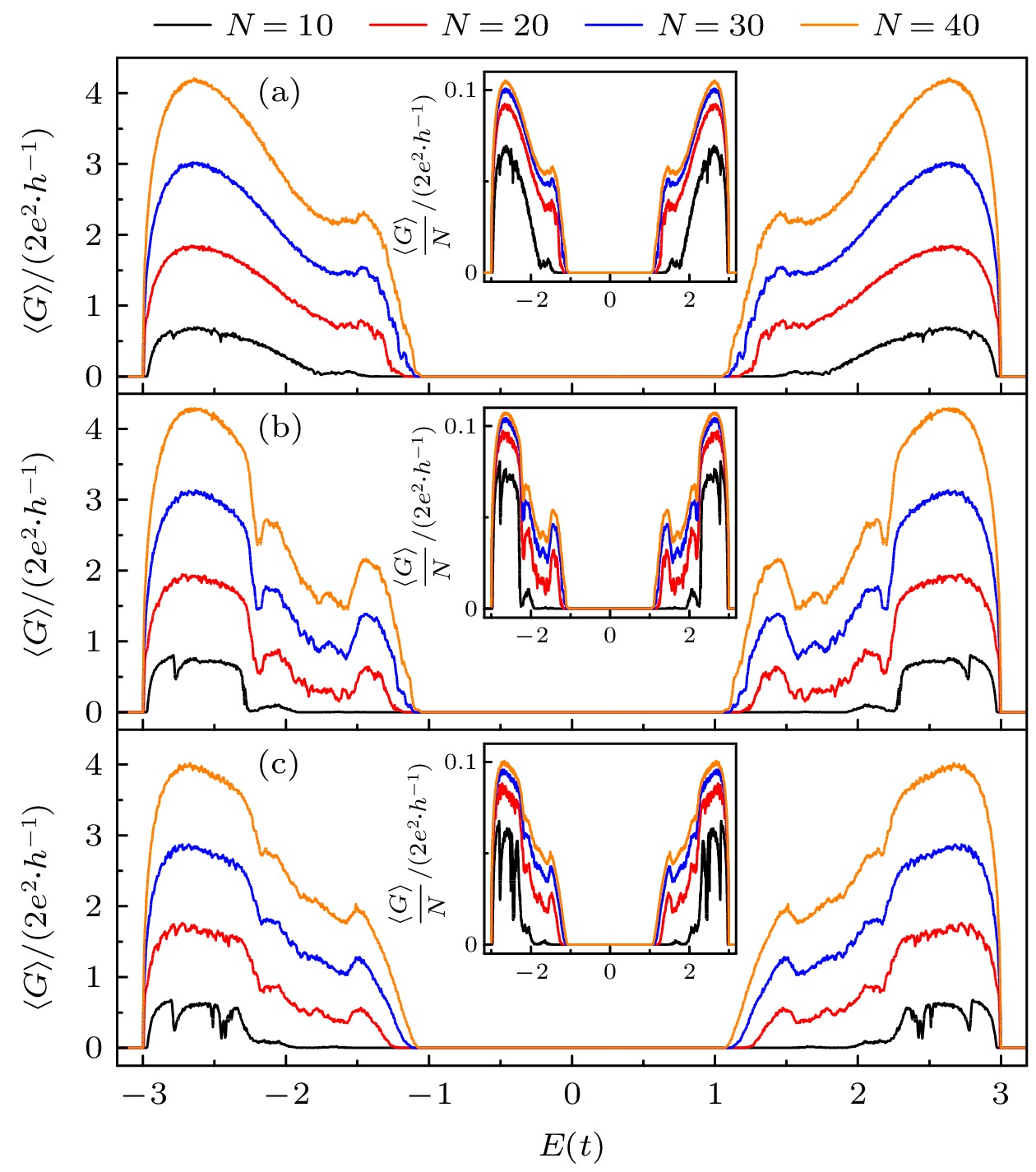
$ \left\langle G \right\rangle $ 随E的变化曲线 (a), (b), (c) 分别对应第I, II和III类无序ZGNRs. 其中插图为重整化电导与E的关系, 重整化电导定义为平均电导与无序ZGNRs宽度的比值. 对于所有ZGNRs: P = 0.5, M = 10000Figure 4.
$ \left\langle G \right\rangle $ as a function of E for three types of disordered ZGNRs for different widths N: (a), (b), (c) correspond to three types of disordered ZGNRs, respectively. Here, the insets denote the renormalized conductance which is defined as the ratio of$ \left\langle G \right\rangle $ to N. P = 0.5 and M = 10000 for all disordered ZGNRs.
图 5 三类无序ZGNRs在费米能级附近的透射能隙Eg随宽度N的关系. 对于所有ZGNRs: P = 0.5, M = 10000
Figure 5. Size of transmission gaps Eg as a function of N for three type of disordered ZGNRs. Here, P = 0.5 and M = 10000 for all ZGNRs.
-
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D E, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Beenakker C W J 2008 Rev. Mod. Phys. 80 1337
Google Scholar
[3] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801
Google Scholar
[4] Xu X R, Cheng S G 2013 J. Phys. Condens. Matter 25 075304
Google Scholar
[5] Huang Y L, Wang K T, Xing Y, Liu G B, Zhao H K 2019 Carbon 143 641
Google Scholar
[6] Cheng S G, Liu H, Jiang H, Sun Q F, Xie X C 2018 Phys. Rev. Lett. 121 156801
Google Scholar
[7] Wei M, Zhou M, Wang B, Xing Y 2020 Phys. Rev. B 102 075432
Google Scholar
[8] 陈兴, 赵晗, 张艳, 刘露, 杨志宏, 宋玲玲 2021 70 198503
Google Scholar
Chen X, Zhao H, Zhang Y, Liu L, Yang Z H, Song L L 2021 Acta Phys. Sin. 70 198503
Google Scholar
[9] Fu H Y, Sun F, Liu R, Suo Y Q, Bi J J, Wang C K, Li Z L 2019 Phys. Lett. A 383 867
Google Scholar
[10] Niu L L, Fu H Y, Suo Y Q, Liu R, Sun F, Wang S S, Zhang G P, Wang C K, Li Z L 2021 Physica E 128 114542
Google Scholar
[11] 刘贵立, 杨忠华 2018 67 076301
Google Scholar
Liu G L, Yang Z H, 2018 Acta Phys. Sin. 67 076301
Google Scholar
[12] 张慧珍, 李金涛, 吕文刚, 杨海方, 唐成春, 顾长志, 李俊杰 2017 66 217301
Google Scholar
Zhang H Z, Li J T, Lv W G, Yang H F, Tang C C, Gu C Z, Li J J 2017 Acta Phys. Sin. 66 217301
Google Scholar
[13] Merino Díez N, Garcia Lekue A, Carbonell Sanromà E, Li J, Corso M, Colazzo L, Sedona F, Sánchez Portal D, Pascual J I, de Oteyza D G 2017 ACS Nano 11 11661
Google Scholar
[14] Zhou M, Jin H, Xing Y 2020 Phys. Rev. Appl. 13 044006
Google Scholar
[15] Hashimoto A, Suenaga K, Gloter A, Urita K, Iijima S 2004 Nature 430 870
Google Scholar
[16] Islam A E, Susner M A, Carpena Núñez J, Back T C, Rao R, Jiang J, Pachter R, Tenney S A, Boeckl J J, Maruyama B 2020 Carbon 166 446
Google Scholar
[17] Lahiri J, Lin Y, Bozkurt P, Oleynik I I, Batzill M 2010 Nat. Nanotechnol. 5 326
Google Scholar
[18] Fei Y, Fu Y, Bai X, Du L, Li Z, Komber H, Low K H, Zhou S, Phillips D L, Feng X, Liu J 2021 J. Am. Chem. Soc. 143 2353
Google Scholar
[19] Liu M, Liu M, She L, Zha Z, Pan J, Li S, Li T, He Y, Cai Z, Wang J, Zheng Y, Qiu X, Zhong D 2017 Nat. Commun. 8 14924
Google Scholar
[20] Fan Q, Yan L, Tripp M W, Krejčí O, Dimosthenous S, Kachel S R, Chen M, Foster A S, Koert U, Liljeroth P 2021 Science 372 852
Google Scholar
[21] Gunlycke D, White C T 2011 Phys. Rev. Lett. 106 136806
Google Scholar
[22] Song J, Liu H, Jiang H, Sun Q F, Xie X C 2012 Phys. Rev. B 86 085437
Google Scholar
[23] Tong Z, Pecchia A, Yam C, Dumitrică T, Frauenheim T 2022 Adv. Energy Mater. 12 2200657
Google Scholar
[24] Kong W, Wang R, Xiao X, Zhan F, Gan L Y, Wei J, Fan J, Wu X 2021 J. Phys. Chem. Lett. 12 10874
Google Scholar
[25] Datta S 1995 Electronic Transport in Mesoscopic Systems (Cambridge: Cambridge University Press)
[26] Zhang Y T, Jiang H, Sun Q F, Xie X C 2010 Phys. Rev. B 81 165404
Google Scholar
[27] Chen L, Ouyang F, Ma S, Fang T F, Guo A M, Sun Q F, 2020 Phys. Rev. B 101 115417
Google Scholar
[28] Hu P J, Wang S X, Chen X F, Gao X H, Fang T F, Guo A M, Sun Q F 2022 Phys. Rev. Appl. 17 024074
Google Scholar
[29] Sancho M L, Sancho J L, Rubio J 1984 J. Phys. F: Met. Phys. 14 1205
Google Scholar
[30] Sancho M L, Sancho J L, Sancho J L, Rubio J 1985 J. Phys. F:Met. Phys. 15 851
Google Scholar
[31] 王雪梅, 刘红 2011 60 047102
Google Scholar
Wang X M, Liu H 2011 Acta Phys. Sin. 60 047102
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3746
- PDF Downloads: 152
- Cited By: 0
