硅纳米结构晶体管中与杂质量子点相关的量子输运

吴歆宇; 韩伟华; 杨富华

doi:10.7498/aps.68.20190095

摘要

在小于10 nm的沟道空间中, 杂质数目和杂质波动范围变得十分有限, 这对器件性能有很大的影响. 局域纳米空间中的电离杂质还能够展现出量子点特性, 为电荷输运提供两个分立的杂质能级. 利用杂质原子作为量子输运构件的硅纳米结构晶体管有望成为未来量子计算电路的基本组成器件. 本文结合安德森定域化理论和Hubbard带模型对单个、分立和耦合杂质原子系统中的量子输运特性进行了综述, 系统介绍了提升杂质原子晶体管工作温度的方法.

关键词:

Abstract

As the characteristic size of the transistor approaches to its physical limit, the effect of impurities on device performance becomes more and more significant. The number of impurities and the range of impurity fluctuation become very limited in channel space less than 10 nm, and ionized impurities in local nano-space can even exhibit quantum dot characteristics, providing two discrete levels for charge transport. The behaviour of carrier tunnelling through quantum dots induced by ionized impurities can reveal the abundant quantum information, such as impurity ionization energy, coulomb interaction energy, electron activation energy, orbital level filling, and spin of local electrons. Quantum transport properties are also different in different doping concentrations because whether the quantum states overlap depends on the impurity atom spacing. The silicon nanostructure transistors using impurity atoms as building blocks of quantum transport are also called dopant atom transistors, which are not only compatible with complementary metal oxide semiconductor (CMOS) technology, but also expected to be the basic components of quantum computing circuits in the future. So far, their operating temperature is relatively low due to the shallow ground state energy level of impurity atoms. It is of great significance to study the quantum transport properties in dopant atom transistors and to observe quantum effects among them at room temperature. In this article, the quantum transport properties in single, discrete and coupled impurity atomic systems are described in detail by combining Anderson localization theory and Hubbard band model. Quantum transport in a discrete impurity atomic system is not only controlled by gate voltage, but also dependent on temperature. The current transport spectrum in the coupled impurity atomic system reveals more complex quantum dot characteristics. Single atom transistor can regulate quantum transport only by one impurity atom, which represents the ultimate scale limit of solid state devices. In addition, the methods of improving the operating temperature of dopant atom transistors are also systematically introduced, thereby laying a foundation for their practical applications.

Keywords:

作者及机构信息

1.
中国科学院半导体研究所, 半导体集成技术工程研究中心, 北京市半导体微纳集成工程技术研究中心, 北京　100083

2.
中国科学院大学, 材料与光电研究中心, 北京　100049

通信作者: 韩伟华, weihua@semi.ac.cn

基金项目: 国家重点研发计划(批准号: 2016YFA0200503)资助的课题.

Authors and contacts

1.
Engineering Research Center of Semiconductor Integrated Technology, Beijing Engineering Research Center of Semiconductor Micro-Nano Integrated Technology, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China

2.
Center of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Han Wei-Hua, weihua@semi.ac.cn

Funds: Project supported by the National Key Research and Development Program of China (Grant No. 2016YFA0200503).

文章全文 : translate this paragraph

参考文献

[1]	Chan V, Rengarajan R, Rovedo N, Wei J 2003 Proceedings of IEEE International Electron Devices Meeting Washington USA, December 8−10, 2003 p381
[2]	Mistry K, Allen C, Auth C 2007 Proceedings of IEEE International Electron Devices Meeting Washington USA, December 10−12, 2007 p247
[3]	Auth C, Allen C, Blattner A 2012 Proceedings of Symposium on VLSI Technology Honolulu USA, June 12−14, 2012 p131
[4]	Colinge J P, Lee C W, Afzalian A, Akhavan N D, Yan R, Ferain I, Razavi P, O’Neill B, Blake A, White M 2010 Nature Nanotech. 5 225 Google Scholar
[5]	Lee C W, Afzalian A, Akhavan N D, Yan R, Ferain I, Colinge J P 2009 Appl. Phys. Lett. 94 053511 Google Scholar
[6]	黎明, 黄如 2018 中国科学: 信息科学 48 963 Li M, Huang R 2018 Sci. Sin. Inform. 48 963
[7]	Asenov A, Watling J R, Brown A R, Ferry D K 2002 J. Comput. Electron. 1 503 Google Scholar
[8]	Taur Y 2002 IBM J. Res. Dev. 46 213 Google Scholar
[9]	李艳萍, 徐静平, 陈卫兵, 许胜国, 季峰 2006 55 3670 Google Scholar Li Y P, Xu J P, Chen W B, Xu S G, Ji F 2006 Acta Phys. Sin. 55 3670 Google Scholar
[10]	曹磊, 刘红侠 2012 61 247303 Google Scholar Cao L, Liu H X 2012 Acta Phys. Sin. 61 247303 Google Scholar
[11]	Je M, Han S, Kim I, Shin H 2000 Solid-State Electron. 44 2207 Google Scholar
[12]	Warren A C, Antoniadis D, Smith H I 1986 Phys. Rev. Lett. 56 1858 Google Scholar
[13]	Rustagi S C, Singh N 2007 IEEE Electr. Device L. 28 909 Google Scholar
[14]	Colinge J P, Xiong W 2006 IEEE Electr. Device L. 27 775 Google Scholar
[15]	Park J T, Kim J Y 2010 Appl. Phys. Lett. 97 172101 Google Scholar
[16]	Li Y M, Yu S M, Hwang J R, Yang F L 2008 IEEE Electr. Device L. 55 1449 Google Scholar
[17]	Akhavan N D, Ferain I, Yu R, Razavi P, Colinge J P 2012 Solid-State Electron. 70 92 Google Scholar
[18]	Ueda A, Luisier M, Sano N 2015 Appl. Phys. Lett. 107 253501 Google Scholar
[19]	Zwanenburg F A, Dzurak A S, Morello A, Simmons M Y, Hollenberg L C L, Klimeck G, Rogge S, Coppersmith S N, Eriksson M A 2013 Rev. Mod. Phys. 85 0034
[20]	Ryu H, Lee S, Fuechsle M, Miwa J A, Mahapatra S, Hollenberg L C L, Simmons M Y, Klimeck G 2015 Small 11 374 Google Scholar
[21]	Moraru D, Udhiarto A, Anwar M, Nowak R, Jablonski R, Hamid E, Tarido J C, Mizuno T, Tabe M 2011 Nanoscale Res. Lett. 6 479 Google Scholar
[22]	Moraru D, Ono Y, Inokawa H, Tabe M 2007 Phys. Rev. B 76 1
[23]	Sellier H, Lansbergen G P, Caro J, Rogge S, Collaert N, Ferain I, Jurczak M, Biesemans S 2007 Appl. Phys. Lett. 90 3
[24]	Barraud S, Berthomé M, Coquand R, Cassé M, Ernst T, Samson M P, Perreau P, Bourdelle K K, Faynot O, Poiroux T 2012 IEEE Electron. Device L. 33 1225 Google Scholar
[25]	Moraru D, Tabe M 2013 Toward Quantum FinFET (Cham: Springer) pp305−324
[26]	Tyryshkin A M, Tojo S, Morton J J L, Riemann H, Abrosimov N V, Becker P, Pohl H J, Schenkel T, Thewalt M L W, Itoh K M, Lyon S A 2012 Nature Mater. 11 143 Google Scholar
[27]	Morello A, Pla J J, Zwanenburg F A, Chan K W, Tan K Y, Hubel H, Mttnen M, Nugroho C D, Yang C Y, van Donkelaar J A, Alves A D C, Jamieson D N, Escott C C, Hollenberg L C L, Clark R G, Dzurak A S 2010 Nature 467 687 Google Scholar
[28]	Fuechsle M, Miwa J A, Mahapatra S, Ryu H, Lee S, Warschkow O, Hollenberg L C L, Klimeck G, Simmons Y M 2012 Nature Nanotech 7 242 Google Scholar
[29]	Tabe M, Moraru D, Ligowski M, Anwar M, Jablonski R, Ono Y, Mizuno T 2010 Appl. Phys. Lett. 105 016803 Google Scholar
[30]	Anwar M, Nowak R, Moraru D, Udhiarto A, Mizuno T, Jablonski R 2011 Appl. Phys. Lett. 99 213101 Google Scholar
[31]	Tyszka K, Moraru D, Samanta A, Mizuno T, Jablonski R, Tabe M 2015 J. Appl. Phys. 117 244307 Google Scholar
[32]	Lee P A, Fisher D S 1981 Phys. Rev. Lett. 47 882 Google Scholar
[33]	蒋祺, 龚昌德 1988 37 941 Google Scholar Jiang Q, Gong C D 1988 Acta Phys. Sin. 37 941 Google Scholar
[34]	Mott N F, Twose W D, 1961 Adv. Phys. 10 107 Google Scholar
[35]	Fleishman L, Licciardello D C, Anderson P W 1978 Phys. Rev. Lett. 40 1340 Google Scholar
[36]	Yu D, Wang C J, Wehrenberg B L, Guyot-Sionnest P 2004 Phys. Rev. Lett. 92 216802 Google Scholar
[37]	Mott N F 1968 J. Non-Cryst. Solids 1 1 Google Scholar
[38]	Mott N F 1987 Conduction in Non-crystalline Materials (New York: Clarendon Press) p1
[39]	Moraru D, Samanta A, Anh L T, Mizuno T, Mizuta H, Tabe M 2014 Sci. Rep. 4 6219
[40]	Moraru D, Samanta A, Tyszka K, Anh L T, Muruganathan M, Mizuno T, Jablonski R, Mizuta H, Tabe M 2015 Nanoscale Res. Lett. 10 372 Google Scholar
[41]	Wauqh F R, Berry M J, Crouch C H, Livermore C, Mar D J, Westervelt R M, Campman K L, Gossard A C 1996 Phys. Rev. B 53 1413
[42]	Shinada T, Okamoto S, Kobayashi T, Ohdomari I 2005 Nature 437 1128 Google Scholar
[43]	Anisimov V I, Zaanen J, Anderson O K 1991 Phys. Rev. B 44 943 Google Scholar
[44]	Prati E, Hori M, Guagliardo F, Ferrari G, Shinada T 2012 Nature Nanotech. 7 443 Google Scholar
[45]	Prati E, Kumagai K, Hori M, Shinada T 2015 Sci. Rep. 6 19704
[46]	Shin S J, Lee J J, Kang H J, Choi J B, Yang S R E, Takahashi Y, Hasko D G 2011 Nano Lett. 11 1591 Google Scholar
[47]	Tan Y, Kamiya T, Durrani Z A, Ahmed H 2003 J. Appl. Phys. 94 663
[48]	Rafiq M A, Masubuchi K, Durrani Z A K, Colli A, Mizuta H, Milne W I, Oda S 2012 J. Appl. Phys. 51 025202 Google Scholar
[49]	Saitoh M, Hiramoto T 2004 Appl. Phys. Lett. 84 3172 Google Scholar
[50]	Deshpande V, Barraud S, Jehl X, Wacquez R, Vinet M, Coquand R, Roche B, Voisin B, Triozon F, Vizioz C 2013 Solid-State Electron. 84 179 Google Scholar
[51]	Lavieville R, Triozon F, Barraud S, Corna A, Jehl X, Sanquer M, Li J, Abisset A, Duchemin I, Niquet Y M 2015 Nano Lett. 15 2958 Google Scholar
[52]	Lee S, Lee Y, Song E B, Hiramoto T 2014 Nano Lett. 14 71 Google Scholar
[53]	Tabe M, Samanta A, Moraru D 2017 Recent Global Research and Education: Technological Challenges (Cham: Springer) p83
[54]	Björk M T, Schmid H, Knoch J, Riel H, Riess W 2008 Nature Nanotech. 4 103
[55]	Diarra M, Niquet Y M, Delerue C, Allan G 2007 Phys. Rev. B 75 045301 Google Scholar
[56]	Pierre M, Wacquez R, Sanquer M, Vinet M, Cueto O 2009 Nature Nanotech. 5 133
[57]	Hamid E, Moraru D, Kuzuya Y, Mizuno T, Anh L T, Mizuta H, Tabe M 2013 Phys. Rev. B 87 085420 Google Scholar
[58]	Samanta A, Muruganathan M, Hori M, Ono Y, Mizuta H, Tabe M, Moraru D 2017 Appl. Phys. Lett. 110 093107 Google Scholar
[59]	Matveev K A, Glazman L I 1996 Phys. Rev. B 54 10339 Google Scholar
[60]	Tamura H, Takahashi Y, Murase K 1999 Microelectron. Eng. 47 205 Google Scholar
[61]	Morgan N Y, Abusch-Magder D, Kastner M A, Takahashi Y, Tamura H, Murase K 2001 J. Appl. Phys. 89 410 Google Scholar
[62]	Durrani Z, Jones M, Abualnaja F, Wang C, Kaestner M, Lenk S, Lenk C, Rangelow W L, Andreev A 2018 J. Appl. Phys. 124 144502 Google Scholar
[63]	Klein M, Lansbergen G P, Mol J A, Rogge S, Levine R D, Remacle F 2009 ChemPhysChem 10 162 Google Scholar
[64]	Klein M, Mol J A, Verduijn J, Lansbergen G P, Rogge S, Levine R D, Remacle F 2010 Appl. Phys. Lett. 96 043107 Google Scholar
[65]	Fresch B, Bocquel J, Hiluf D, Rogge S, Levine R D, Remacle F 2017 ChemPhysChem 18 1790 Google Scholar

施引文献

图 1 电离杂质形成的势阱结构^[19]

Fig. 1. Confinement potential induced by ionizing impurity^[19].

下载: 全尺寸图片幻灯片

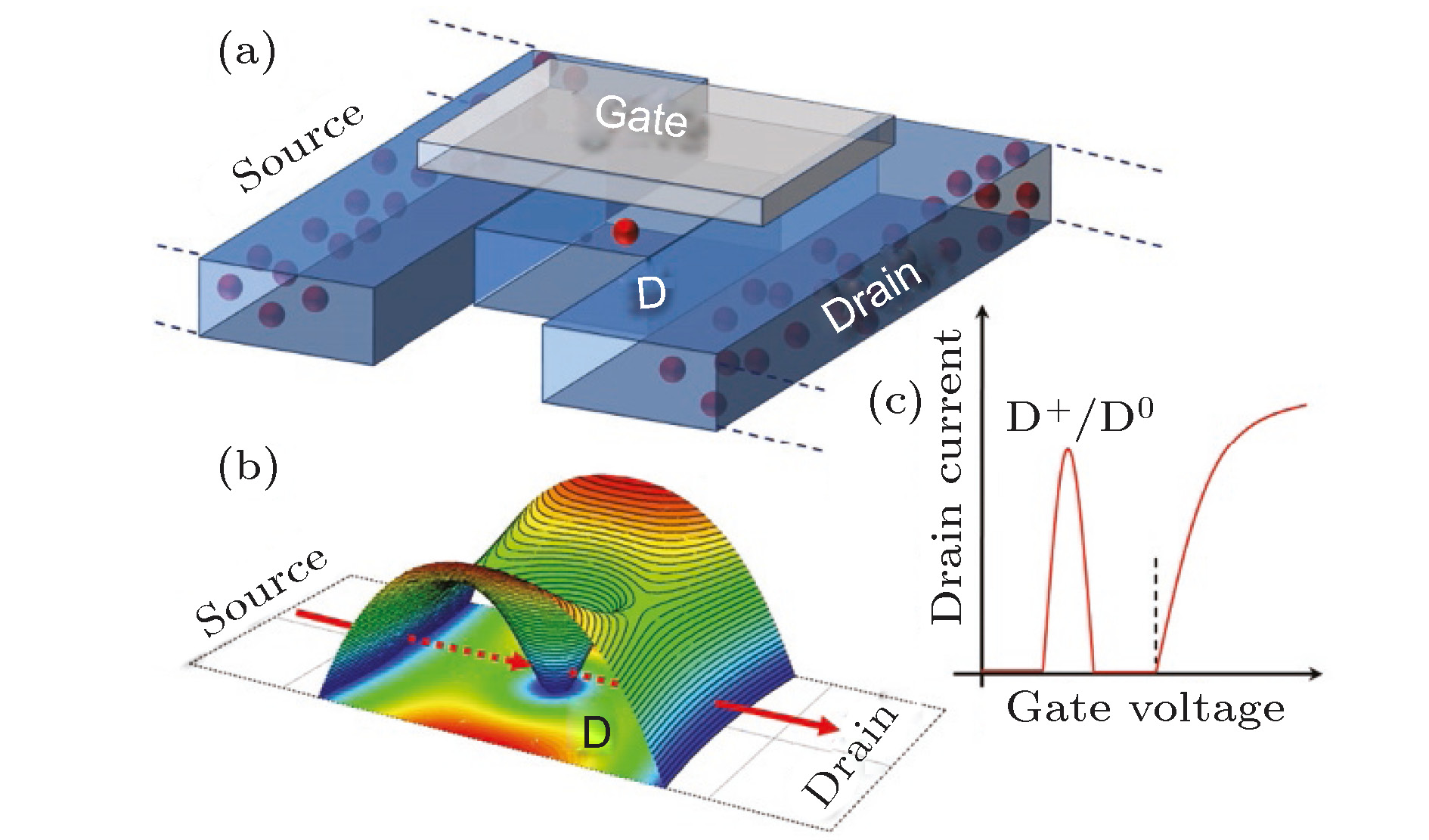
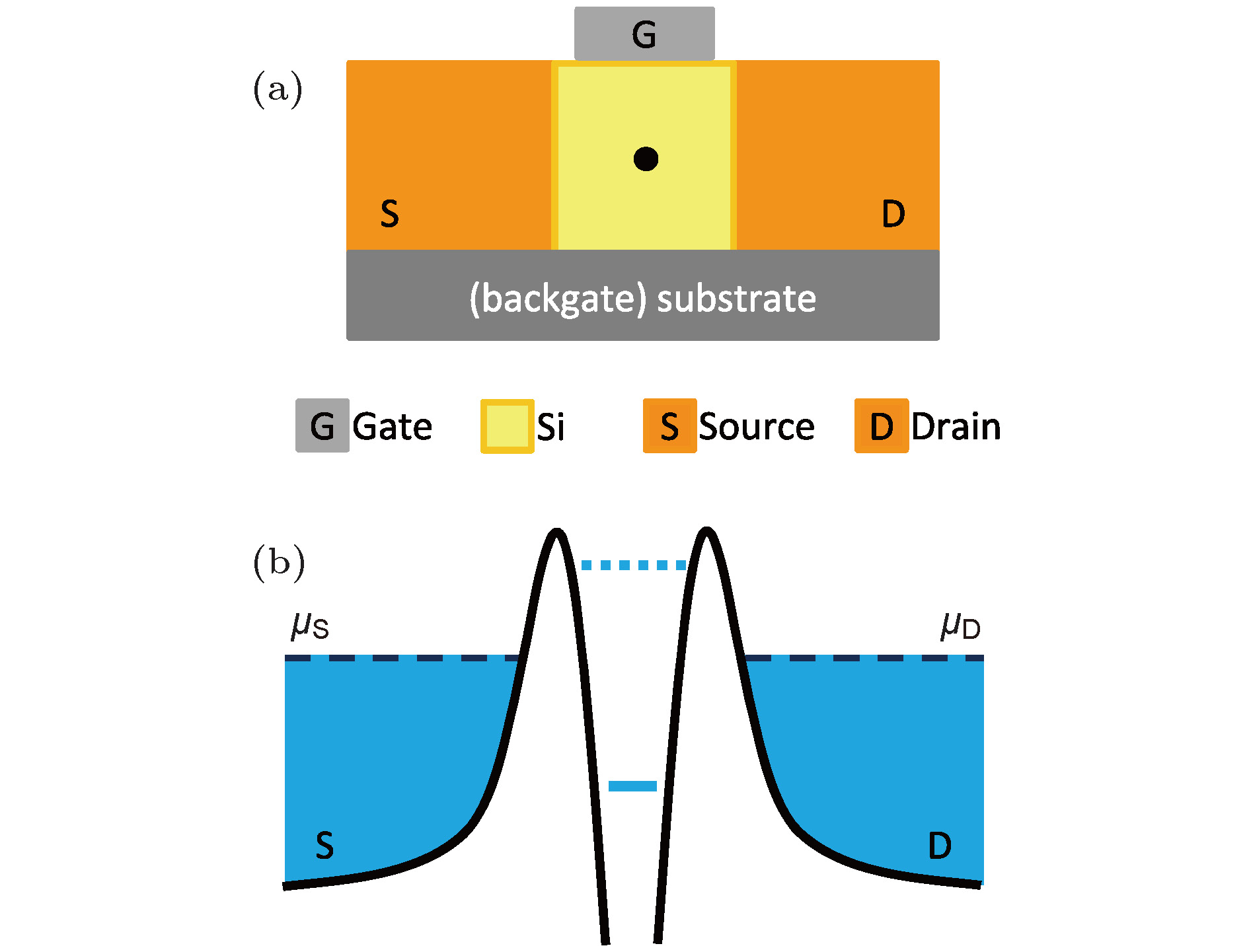
图 2 理想单杂质晶体管的基本结构和工作原理图　(a)单杂质晶体管结构示意图; (b)施主原子调制源端到漏端的单电子隧穿; (c)低温下单杂质晶体管的转移特性曲线^[25]

Fig. 2. Structure and schematic diagram of the ideal single-dopant transistor: (a) Schematic illustration of single-dopant transistor; (b) donor mediates single-electron tunneling from source to drain; (c) transfer characteristics for single-dopant transistor in the low temperature^[25].

下载: 全尺寸图片幻灯片

图 3 (a)单原子晶体管器件结构 STM 图像; (b)局部放大图^[28]

Fig. 3. (a) Perspective STM image of single-atom transistor; (b) close-up of the inner device area^[28].

下载: 全尺寸图片幻灯片

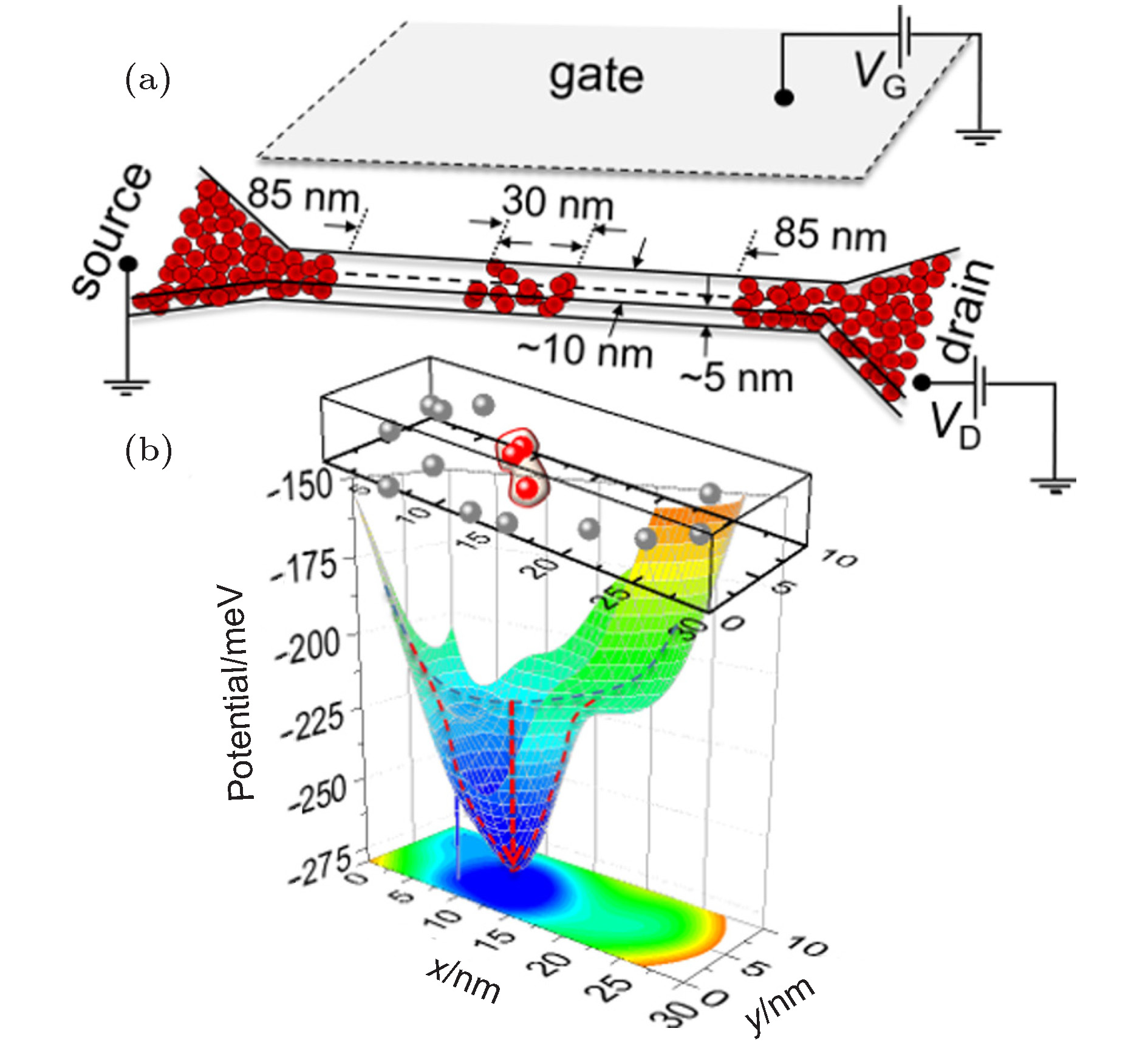
图 4 (a)短沟道器件示意图; (b)短沟道器件电势分布图; (c)短沟道器件I_sd -V_g特性曲线(V_sd = 5 mV); (d)长沟道器件示意图; (e)长沟道器件电势分布图; (f)长沟道器件I_sd -V_g特性曲线(V_sd = 5 mV)^[29]

Fig. 4. (a) Schematic channel structure; (b) example of simulated potential profile; (c) example of dc I_sd -V_g characteristics (V_sd = 5 mV) for a short-channel FET; (d) schematic channel structure; (e) example of simulated potential profile; (f) example of dc I_sd -V_g chara-cteristics (V_sd = 5 mV) for a long-channel FET^[29].

下载: 全尺寸图片幻灯片

图 5 (a)不同沟道长度下分裂峰个数的实验统计; (b)不同沟道长度下量子点个数的模拟统计; (c) 50 nm × 50 nm纳米结构中一个量子点中的平均杂质数目^[29]

Fig. 5. (a) Statistical results of the number of subpeaks; (b) statistical results of the number of dopant-induced QDs; (c) average number of dopants embedded in one QD for 50 nm × 50 nm nanostructures^[29].

下载: 全尺寸图片幻灯片

图 6 (a)低温下随栅压变化的电势分布图; (b)分立的磷施主原子在不同栅压下逐个电中性化^[30]

Fig. 6. (a) Sequence of electronic potential landscapes as a function of applied V_BG; (b) a simple illustration of one-by-one neutralization of individual P-donors at different V_BG^[30].

下载: 全尺寸图片幻灯片

图 7 (a) SOI-FET低温下的I_D-V_G特性曲线; (b)沟道中可能的杂质原子分布以及沟道电势分布示意图^[31]

Fig. 7. (a) Low-temperature source-drain current (I_D) vs. gate voltage (V_G) characteristics; (b) one possible P-donors’ distribution and schematic channel potential profiles^[31].

下载: 全尺寸图片幻灯片

图 8 无序系统中的带尾定域态^[32]

Fig. 8. Tailed localized states in disordered systems^[32].

下载: 全尺寸图片幻灯片

图 9 弱杂质补偿和强杂质补偿情况下的能带和定域态空间分布示意图　(a)弱杂质补偿; (b)强杂质补偿^[34]

Fig. 9. Schematic representation of the energy and space distribution of the localized states in the case of weak (a) and strong (b) compensation^[34].

下载: 全尺寸图片幻灯片

图 10 电子的跃迁方式　(a)可变程跃迁; (b)最近邻跃迁^[38]

Fig. 10. Hopping modes of the electron: (a) Variable range hopping; (b) nearest neighbor hopping^[38].

下载: 全尺寸图片幻灯片

图 11 (a)开尔文探针力显微镜测量SOI-FETs的结构示意图; (b), (c)不同掺杂浓度下, 施主原子形成的电势分布图^[39]

Fig. 11. (a) Schematic of KPFM measurement setup; (b), (c) potential distribution of donor atoms at different doping concentrations^[39]

下载: 全尺寸图片幻灯片

图 12 (a) SOI-FET低温下的I_D-V_G特性曲线; (b)选择性掺杂沟道中可能的杂质原子分布以及沟道电势分布示意图^[31]

Fig. 12. (a) Low-temperature source-drain current (I_D) vs gate voltage (V_G) characteristics; (b) a possible P-donors’ distribution and schematic channel potential profiles in the selective doping channel^[31].

下载: 全尺寸图片幻灯片

图 13 Hubbard能带模型^[43]

Fig. 13. Hubbard band model^[43].

下载: 全尺寸图片幻灯片

图 14 不同杂质数目下的量子输运特征, 从单施主态到杂质带的安德森-莫特转变^[44]

Fig. 14. Anderson-Mott transition probed by means of quantum transport^[44].

下载: 全尺寸图片幻灯片

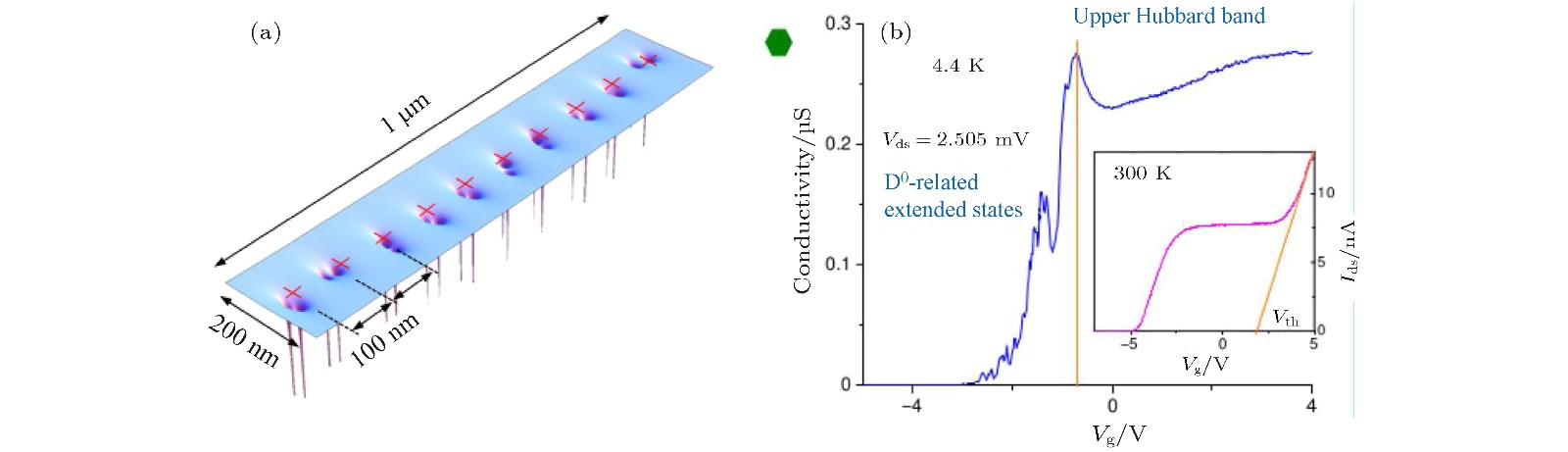
图 15 (a)沿沟道分布的20个磷施主原子中电势分布的理想示意图; (b)V_ds = 2.505 mV时, 在4.4 K下测量的器件电导-栅压曲线. 插图: V_ds = 2.505 mV时, 室温下提取的阈值电压^[45]

Fig. 15. (a) An idealized representation of the potential distributions in the 20 phosphorous donors distributed along the channel of the sample; (b) conductance σ of the device probed at 4.4 K measured at V_ds = 2.505 mV. Inlet: extraction of the threshold voltage at room temperature, at V_ds = 2.505 mV^[45].

下载: 全尺寸图片幻灯片

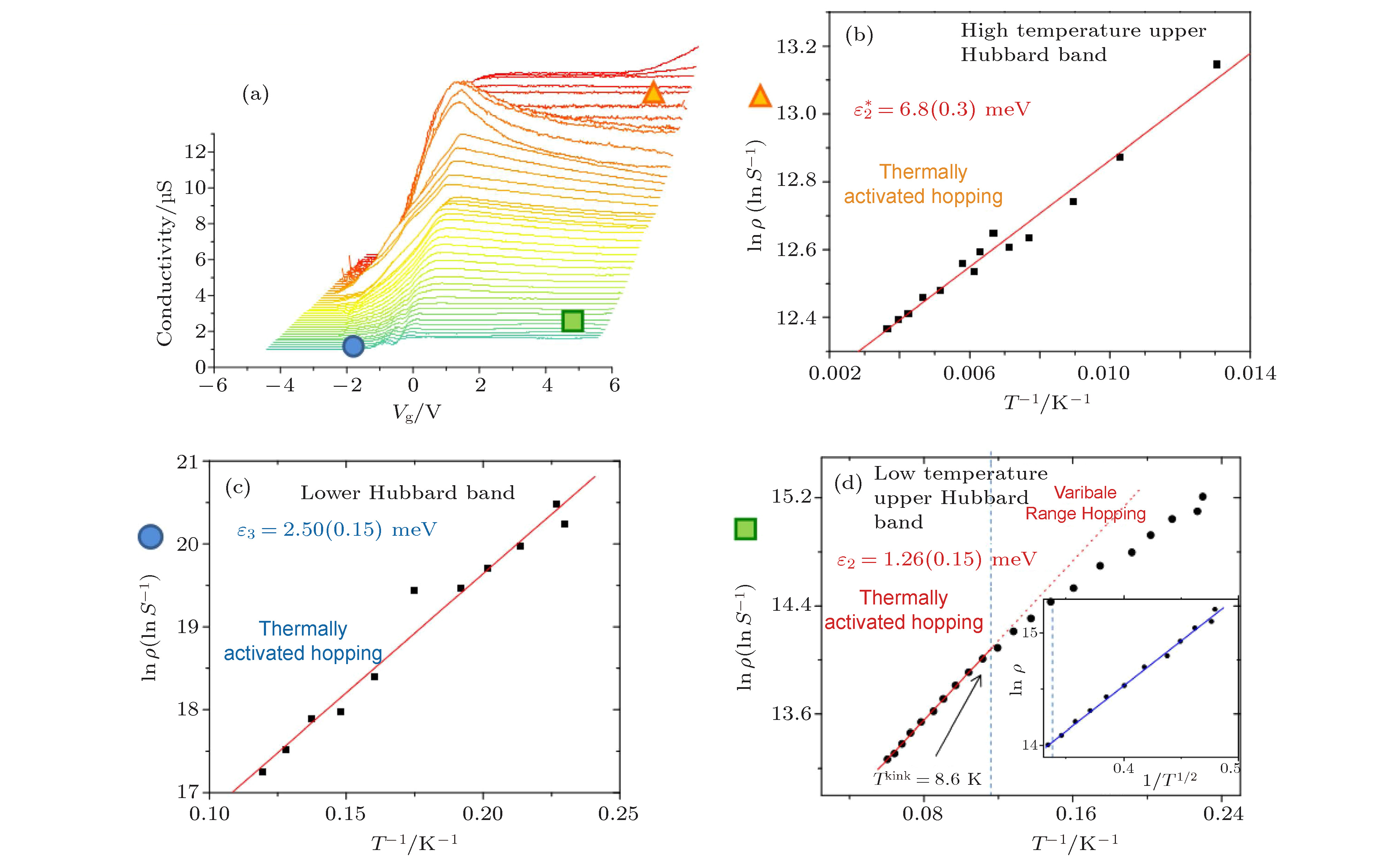
图 16 (a)4.2—274 K温度区间下的电导-栅压曲线; (b)高温下上Hubbard带的热激活输运; (c)低温下下Hubbard带的热激活输运; (d)低温下上Hubbard带的热激活输运^[45]

Fig. 16. (a) The conductance as a function of the gate voltage V_g from 4.2 to 274 K; (b) the thermal activation of the upper Hubbard band at high temperature; (c) the thermal activation of the lower Hubbard band at low temperature; (d) the thermal activation of the upper Hubbard band at low temperature^[45].

下载: 全尺寸图片幻灯片

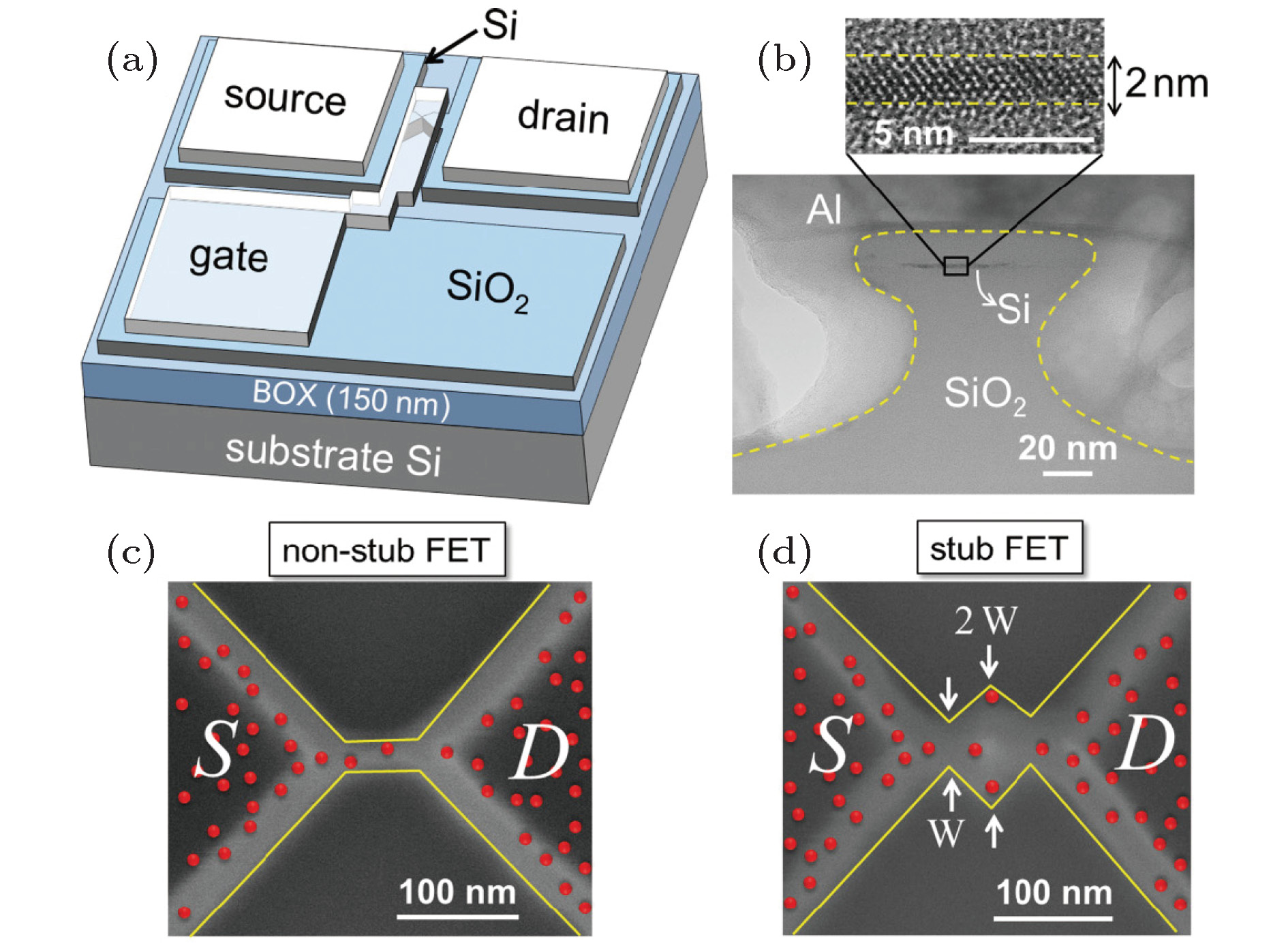
图 17 (a)单电子晶体管结构示意图; (b)化学湿法腐蚀后硅纳米线扫描电子显微镜(SEM)图; (c)形成围栅GAA结构后硅纳米线透射电子显微镜(TEM)图; (d)制备的单电子晶体管在150−300 K下的I_D-V_G特性曲线^[52]

Fig. 17. (a) Schematic configuration of the fabricated Si SET; (b) scanning electron microscopy image of the Si nanowire after chemical wet-etching; (c) transmission electron microscopy image of the Si nanowire after fabricating the GAA structure; (d) I_D−V_G characteristic curves of the fabricated SET at T = 150−300 K^[52].

下载: 全尺寸图片幻灯片

图 18 (a)杂质原子晶体管结构示意图; (b)杂质在器件沟道中提供确定的两个能级^[19]

Fig. 18. (a) Schematic of dopant atom transistor; (b) two determined levels provided by impurity in device^[19].

下载: 全尺寸图片幻灯片

图 19 磷原子的基态能级随硅纳米线直径的减小而加深^[53]

Fig. 19. Ground state of phosphorous donor becomes deeper with decreasing radius of Si nanowire^[53].

下载: 全尺寸图片幻灯片

图 20 (a)没有和(b)有介电限制时杂质原子的电离能随纳米线半径的变化曲线图^[55]

Fig. 20. Ionization energy E_I vs. the wire radius R for donor impurities: (a) Without dielectric confinement; (b) with dielectric confinement^[55].

下载: 全尺寸图片幻灯片

图 21 (a) SOI晶体管结构示意图; (b)器件沟道TEM图; (c)原纳米线结构; (d) stub纳米线结构^[57]

Fig. 21. (a) Schematic of SOI transistor; (b) TEM image taken across the device channel; (c) SEM images of non-stub channel and (d) stub channel^[57].

下载: 全尺寸图片幻灯片

图 22 基态电子的束缚能随耦合原子数目的增加而增大^[53]

Fig. 22. Binding energy of clustered donors is shown for different N^[53].

下载: 全尺寸图片幻灯片

图 23 (a)选择性掺杂硅纳米沟道; (b)选择性掺杂区域模拟的最深势阱分布^[58]

Fig. 23. (a) The selectively-doped Si nanoscale channel; (b) atomistic representation of the potential landscape simulated for a selectively-doped area with deepest potential well^[58].

下载: 全尺寸图片幻灯片

图 24 (a)沟道选择性掺杂和(b)沟道未掺杂SOI-FET在不同温度下的I_D-V_G特性曲线^[58]

Fig. 24. (a) and (b) IDS-VG characteristics as a function of temperature for a selectively-doped-channel SOI-FET (up to 300 K) and for a non-doped-channel SOI-FET (up to 160 K)^[58].

下载: 全尺寸图片幻灯片

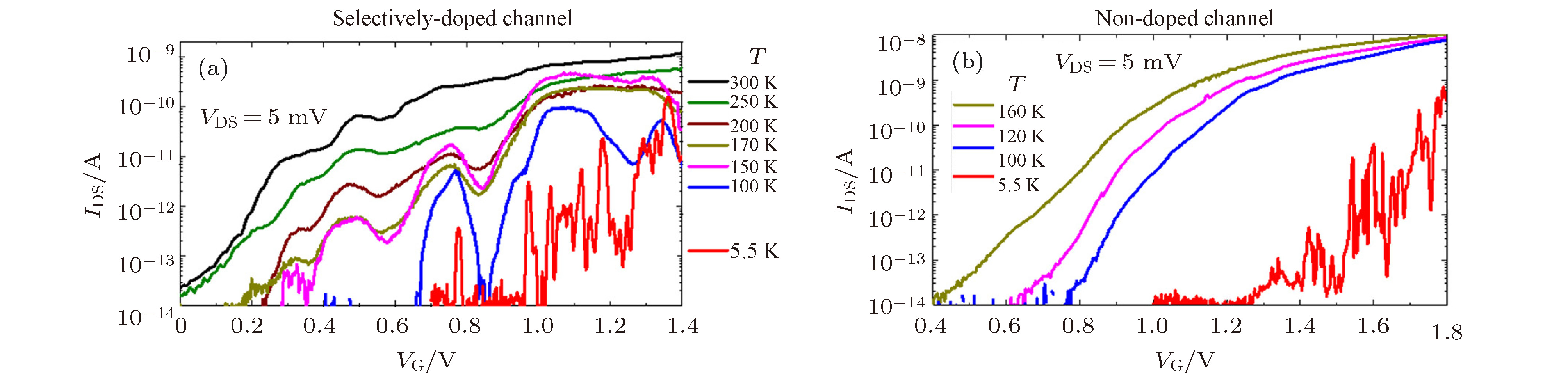
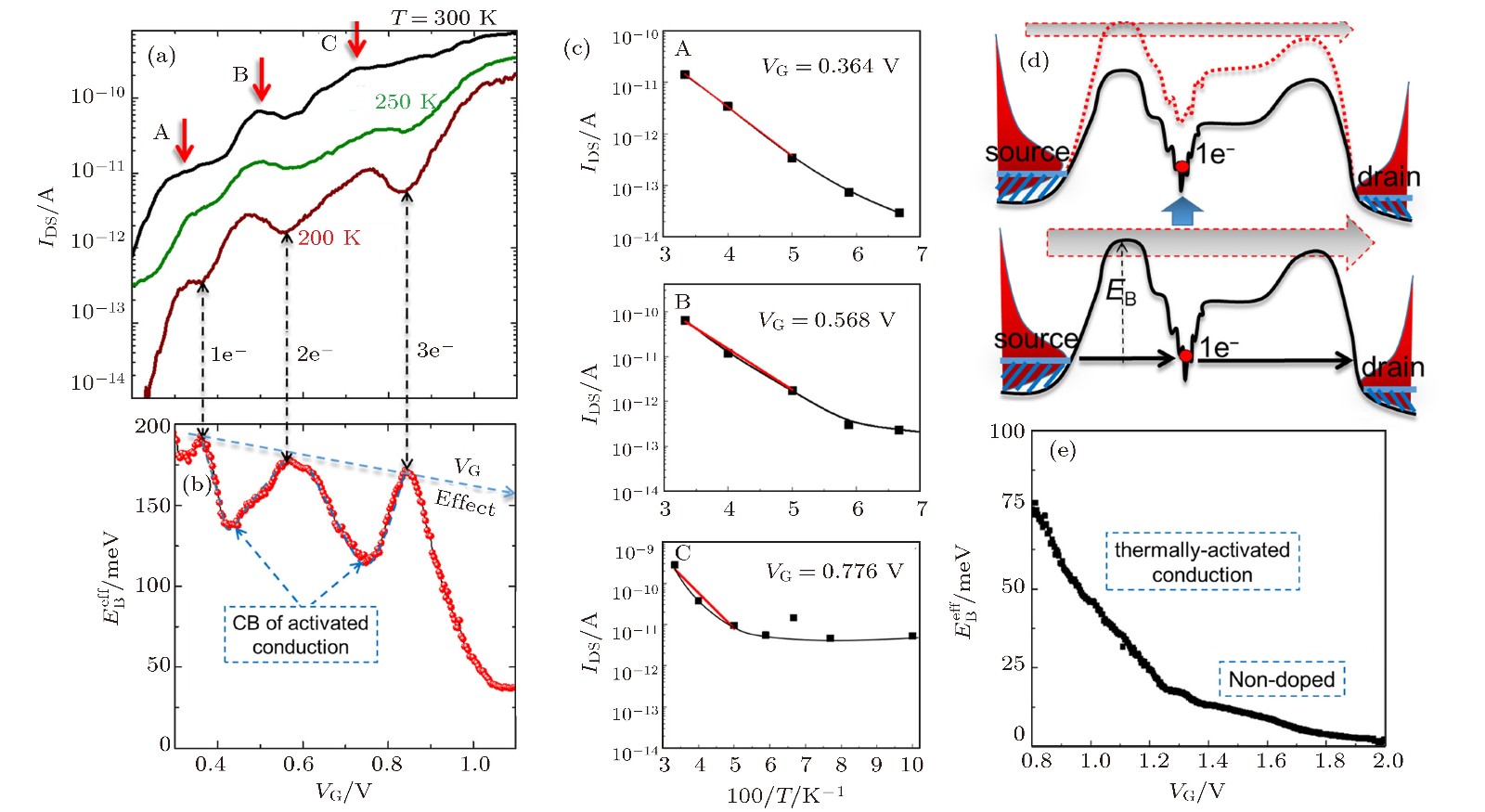
图 25 (a)不同温度下, 沟道选择性掺杂SOI-FET器件I_DS-V_G特性曲线; (b)有效势垒高度随栅压V_G的变化; (c)不同电流峰对应的Arrhenius曲线; (d)激活传导的库仑阻塞机制(下图), 量子点俘获电子的库仑阻塞情形(上图); (e)沟道未掺杂SOI-FET器件仅仅表现出热激活传导性质^[58]

Fig. 25. (a) I_DS-V_G characteristics as a function of temperature for the selectively-doped channel SOI-FET; (b) effective barrier height (E_Beff) estimated from Arrhenius plots as a function of V_G; (c) arrhenius plots for V_G corresponding to different peaks; (d) schematic illustrations of the mechanism of Coulomb blockade of activated conduction for the single-electron tunneling current peak (lower panel) and for the Coulomb blockade condition with an electron trapped in the QD (upper panel); (e) E_Beff extracted for a non-doped-channel SOI-FET, exhibiting only behavior typical of thermally-activated conduction^[58].

下载: 全尺寸图片幻灯片

图 26 (a)点接触式量子点晶体管结构示意图; (b)点接触区域的能带示意图^[62]

Fig. 26. (a) Schematic of the point contact QD transistor; (b) schematic representation of the energy diagram across the point-contact region^[62].

下载: 全尺寸图片幻灯片

map

[1]	Chan V, Rengarajan R, Rovedo N, Wei J 2003 Proceedings of IEEE International Electron Devices Meeting Washington USA, December 8−10, 2003 p381
[2]	Mistry K, Allen C, Auth C 2007 Proceedings of IEEE International Electron Devices Meeting Washington USA, December 10−12, 2007 p247
[3]	Auth C, Allen C, Blattner A 2012 Proceedings of Symposium on VLSI Technology Honolulu USA, June 12−14, 2012 p131
[4]	Colinge J P, Lee C W, Afzalian A, Akhavan N D, Yan R, Ferain I, Razavi P, O’Neill B, Blake A, White M 2010 Nature Nanotech. 5 225 Google Scholar
[5]	Lee C W, Afzalian A, Akhavan N D, Yan R, Ferain I, Colinge J P 2009 Appl. Phys. Lett. 94 053511 Google Scholar
[6]	黎明, 黄如 2018 中国科学: 信息科学 48 963 Li M, Huang R 2018 Sci. Sin. Inform. 48 963
[7]	Asenov A, Watling J R, Brown A R, Ferry D K 2002 J. Comput. Electron. 1 503 Google Scholar
[8]	Taur Y 2002 IBM J. Res. Dev. 46 213 Google Scholar
[9]	李艳萍, 徐静平, 陈卫兵, 许胜国, 季峰 2006 55 3670 Google Scholar Li Y P, Xu J P, Chen W B, Xu S G, Ji F 2006 Acta Phys. Sin. 55 3670 Google Scholar
[10]	曹磊, 刘红侠 2012 61 247303 Google Scholar Cao L, Liu H X 2012 Acta Phys. Sin. 61 247303 Google Scholar
[11]	Je M, Han S, Kim I, Shin H 2000 Solid-State Electron. 44 2207 Google Scholar
[12]	Warren A C, Antoniadis D, Smith H I 1986 Phys. Rev. Lett. 56 1858 Google Scholar
[13]	Rustagi S C, Singh N 2007 IEEE Electr. Device L. 28 909 Google Scholar
[14]	Colinge J P, Xiong W 2006 IEEE Electr. Device L. 27 775 Google Scholar
[15]	Park J T, Kim J Y 2010 Appl. Phys. Lett. 97 172101 Google Scholar
[16]	Li Y M, Yu S M, Hwang J R, Yang F L 2008 IEEE Electr. Device L. 55 1449 Google Scholar
[17]	Akhavan N D, Ferain I, Yu R, Razavi P, Colinge J P 2012 Solid-State Electron. 70 92 Google Scholar
[18]	Ueda A, Luisier M, Sano N 2015 Appl. Phys. Lett. 107 253501 Google Scholar
[19]	Zwanenburg F A, Dzurak A S, Morello A, Simmons M Y, Hollenberg L C L, Klimeck G, Rogge S, Coppersmith S N, Eriksson M A 2013 Rev. Mod. Phys. 85 0034
[20]	Ryu H, Lee S, Fuechsle M, Miwa J A, Mahapatra S, Hollenberg L C L, Simmons M Y, Klimeck G 2015 Small 11 374 Google Scholar
[21]	Moraru D, Udhiarto A, Anwar M, Nowak R, Jablonski R, Hamid E, Tarido J C, Mizuno T, Tabe M 2011 Nanoscale Res. Lett. 6 479 Google Scholar
[22]	Moraru D, Ono Y, Inokawa H, Tabe M 2007 Phys. Rev. B 76 1
[23]	Sellier H, Lansbergen G P, Caro J, Rogge S, Collaert N, Ferain I, Jurczak M, Biesemans S 2007 Appl. Phys. Lett. 90 3
[24]	Barraud S, Berthomé M, Coquand R, Cassé M, Ernst T, Samson M P, Perreau P, Bourdelle K K, Faynot O, Poiroux T 2012 IEEE Electron. Device L. 33 1225 Google Scholar
[25]	Moraru D, Tabe M 2013 Toward Quantum FinFET (Cham: Springer) pp305−324
[26]	Tyryshkin A M, Tojo S, Morton J J L, Riemann H, Abrosimov N V, Becker P, Pohl H J, Schenkel T, Thewalt M L W, Itoh K M, Lyon S A 2012 Nature Mater. 11 143 Google Scholar
[27]	Morello A, Pla J J, Zwanenburg F A, Chan K W, Tan K Y, Hubel H, Mttnen M, Nugroho C D, Yang C Y, van Donkelaar J A, Alves A D C, Jamieson D N, Escott C C, Hollenberg L C L, Clark R G, Dzurak A S 2010 Nature 467 687 Google Scholar
[28]	Fuechsle M, Miwa J A, Mahapatra S, Ryu H, Lee S, Warschkow O, Hollenberg L C L, Klimeck G, Simmons Y M 2012 Nature Nanotech 7 242 Google Scholar
[29]	Tabe M, Moraru D, Ligowski M, Anwar M, Jablonski R, Ono Y, Mizuno T 2010 Appl. Phys. Lett. 105 016803 Google Scholar
[30]	Anwar M, Nowak R, Moraru D, Udhiarto A, Mizuno T, Jablonski R 2011 Appl. Phys. Lett. 99 213101 Google Scholar
[31]	Tyszka K, Moraru D, Samanta A, Mizuno T, Jablonski R, Tabe M 2015 J. Appl. Phys. 117 244307 Google Scholar
[32]	Lee P A, Fisher D S 1981 Phys. Rev. Lett. 47 882 Google Scholar
[33]	蒋祺, 龚昌德 1988 37 941 Google Scholar Jiang Q, Gong C D 1988 Acta Phys. Sin. 37 941 Google Scholar
[34]	Mott N F, Twose W D, 1961 Adv. Phys. 10 107 Google Scholar
[35]	Fleishman L, Licciardello D C, Anderson P W 1978 Phys. Rev. Lett. 40 1340 Google Scholar
[36]	Yu D, Wang C J, Wehrenberg B L, Guyot-Sionnest P 2004 Phys. Rev. Lett. 92 216802 Google Scholar
[37]	Mott N F 1968 J. Non-Cryst. Solids 1 1 Google Scholar
[38]	Mott N F 1987 Conduction in Non-crystalline Materials (New York: Clarendon Press) p1
[39]	Moraru D, Samanta A, Anh L T, Mizuno T, Mizuta H, Tabe M 2014 Sci. Rep. 4 6219
[40]	Moraru D, Samanta A, Tyszka K, Anh L T, Muruganathan M, Mizuno T, Jablonski R, Mizuta H, Tabe M 2015 Nanoscale Res. Lett. 10 372 Google Scholar
[41]	Wauqh F R, Berry M J, Crouch C H, Livermore C, Mar D J, Westervelt R M, Campman K L, Gossard A C 1996 Phys. Rev. B 53 1413
[42]	Shinada T, Okamoto S, Kobayashi T, Ohdomari I 2005 Nature 437 1128 Google Scholar
[43]	Anisimov V I, Zaanen J, Anderson O K 1991 Phys. Rev. B 44 943 Google Scholar
[44]	Prati E, Hori M, Guagliardo F, Ferrari G, Shinada T 2012 Nature Nanotech. 7 443 Google Scholar
[45]	Prati E, Kumagai K, Hori M, Shinada T 2015 Sci. Rep. 6 19704
[46]	Shin S J, Lee J J, Kang H J, Choi J B, Yang S R E, Takahashi Y, Hasko D G 2011 Nano Lett. 11 1591 Google Scholar
[47]	Tan Y, Kamiya T, Durrani Z A, Ahmed H 2003 J. Appl. Phys. 94 663
[48]	Rafiq M A, Masubuchi K, Durrani Z A K, Colli A, Mizuta H, Milne W I, Oda S 2012 J. Appl. Phys. 51 025202 Google Scholar
[49]	Saitoh M, Hiramoto T 2004 Appl. Phys. Lett. 84 3172 Google Scholar
[50]	Deshpande V, Barraud S, Jehl X, Wacquez R, Vinet M, Coquand R, Roche B, Voisin B, Triozon F, Vizioz C 2013 Solid-State Electron. 84 179 Google Scholar
[51]	Lavieville R, Triozon F, Barraud S, Corna A, Jehl X, Sanquer M, Li J, Abisset A, Duchemin I, Niquet Y M 2015 Nano Lett. 15 2958 Google Scholar
[52]	Lee S, Lee Y, Song E B, Hiramoto T 2014 Nano Lett. 14 71 Google Scholar
[53]	Tabe M, Samanta A, Moraru D 2017 Recent Global Research and Education: Technological Challenges (Cham: Springer) p83
[54]	Björk M T, Schmid H, Knoch J, Riel H, Riess W 2008 Nature Nanotech. 4 103
[55]	Diarra M, Niquet Y M, Delerue C, Allan G 2007 Phys. Rev. B 75 045301 Google Scholar
[56]	Pierre M, Wacquez R, Sanquer M, Vinet M, Cueto O 2009 Nature Nanotech. 5 133
[57]	Hamid E, Moraru D, Kuzuya Y, Mizuno T, Anh L T, Mizuta H, Tabe M 2013 Phys. Rev. B 87 085420 Google Scholar
[58]	Samanta A, Muruganathan M, Hori M, Ono Y, Mizuta H, Tabe M, Moraru D 2017 Appl. Phys. Lett. 110 093107 Google Scholar
[59]	Matveev K A, Glazman L I 1996 Phys. Rev. B 54 10339 Google Scholar
[60]	Tamura H, Takahashi Y, Murase K 1999 Microelectron. Eng. 47 205 Google Scholar
[61]	Morgan N Y, Abusch-Magder D, Kastner M A, Takahashi Y, Tamura H, Murase K 2001 J. Appl. Phys. 89 410 Google Scholar
[62]	Durrani Z, Jones M, Abualnaja F, Wang C, Kaestner M, Lenk S, Lenk C, Rangelow W L, Andreev A 2018 J. Appl. Phys. 124 144502 Google Scholar
[63]	Klein M, Lansbergen G P, Mol J A, Rogge S, Levine R D, Remacle F 2009 ChemPhysChem 10 162 Google Scholar
[64]	Klein M, Mol J A, Verduijn J, Lansbergen G P, Rogge S, Levine R D, Remacle F 2010 Appl. Phys. Lett. 96 043107 Google Scholar
[65]	Fresch B, Bocquel J, Hiluf D, Rogge S, Levine R D, Remacle F 2017 ChemPhysChem 18 1790 Google Scholar

[1]	高建华, 盛欣力, 王群, 庄鹏飞. 费米子的相对论自旋输运理论. , 2023, 72(11): 112501. doi: 10.7498/aps.72.20222470
[2]	刘天, 李宗良, 张延惠, 蓝康. 耗散环境单量子点体系输运过程的量子速度极限研究. , 2023, 72(4): 047301. doi: 10.7498/aps.72.20222159
[3]	丁锦廷, 胡沛佳, 郭爱敏. 线缺陷石墨烯纳米带的电输运研究. , 2023, 72(15): 157301. doi: 10.7498/aps.72.20230502
[4]	汤家鑫, 范志强, 邓小清, 张振华. 非金属原子掺杂的GaN纳米管: 电子结构、输运特性及电场调控效应. , 2022, 71(11): 116101. doi: 10.7498/aps.71.20212342
[5]	方静云, 孙庆丰. 石墨烯p-n结在磁场中的电输运热耗散. , 2022, 71(12): 127203. doi: 10.7498/aps.71.20220029
[6]	胡海涛, 郭爱敏. 双层硼烯纳米带的量子输运研究. , 2022, 71(22): 227301. doi: 10.7498/aps.71.20221304
[7]	闫婕, 魏苗苗, 邢燕霞. HgTe/CdTe量子阱中自旋拓扑态的退相干效应. , 2019, 68(22): 227301. doi: 10.7498/aps.68.20191072
[8]	闫瑞, 吴泽文, 谢稳泽, 李丹, 王音. 导线非共线的分子器件输运性质的第一性原理研究. , 2018, 67(9): 097301. doi: 10.7498/aps.67.20172221
[9]	李兆国, 张帅, 宋凤麒. 拓扑绝缘体的普适电导涨落. , 2015, 64(9): 097202. doi: 10.7498/aps.64.097202
[10]	李振武. Kondo效应对磁杂质碳纳米管电输运特性的影响. , 2013, 62(9): 096101. doi: 10.7498/aps.62.096101
[11]	刘兴辉, 赵宏亮, 李天宇, 张仁, 李松杰, 葛春华. 基于异质双栅电极结构提高碳纳米管场效应晶体管电子输运效率. , 2013, 62(14): 147308. doi: 10.7498/aps.62.147308
[12]	强蕾, 姚若河. 非晶硅薄膜晶体管沟道中阈值电压及温度的分布. , 2012, 61(8): 087303. doi: 10.7498/aps.61.087303
[13]	刘兴辉, 张俊松, 王绩伟, 敖强, 王震, 马迎, 李新, 王振世, 王瑞玉. 基于非平衡Green函数理论的峰值掺杂-低掺杂漏结构碳纳米管场效应晶体管输运研究. , 2012, 61(10): 107302. doi: 10.7498/aps.61.107302
[14]	孙伟峰. (InAs)1/(GaSb)1超晶格原子链的第一原理研究. , 2012, 61(11): 117104. doi: 10.7498/aps.61.117104
[15]	张彩霞, 郭虹, 杨致, 骆游桦. 三明治结构Tan(B3N3H6)n+1 团簇的磁性和量子输运性质. , 2012, 61(19): 193601. doi: 10.7498/aps.61.193601
[16]	刘玉荣, 陈伟, 廖荣. 低工作电压聚噻吩薄膜晶体管. , 2010, 59(11): 8088-8092. doi: 10.7498/aps.59.8088
[17]	付邦, 邓文基. 任意正多边形量子环自旋输运的普遍解. , 2010, 59(4): 2739-2745. doi: 10.7498/aps.59.2739
[18]	李鹏, 邓文基. 正多边形量子环自旋输运的严格解. , 2009, 58(4): 2713-2719. doi: 10.7498/aps.58.2713
[19]	尹永琦, 李华, 马佳宁, 贺泽龙, 王选章. 多端耦合量子点分子桥的量子输运特性研究. , 2009, 58(6): 4162-4167. doi: 10.7498/aps.58.4162
[20]	陈立, 毛邦宁, 王煜博, 王丽敏, 潘佰良. 低气压下CuBr激光的光谱结构. , 2007, 56(10): 5808-5812. doi: 10.7498/aps.56.5808

计量

文章访问数: 12159
PDF下载量: 88
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

硅纳米结构晶体管中与杂质量子点相关的量子输运