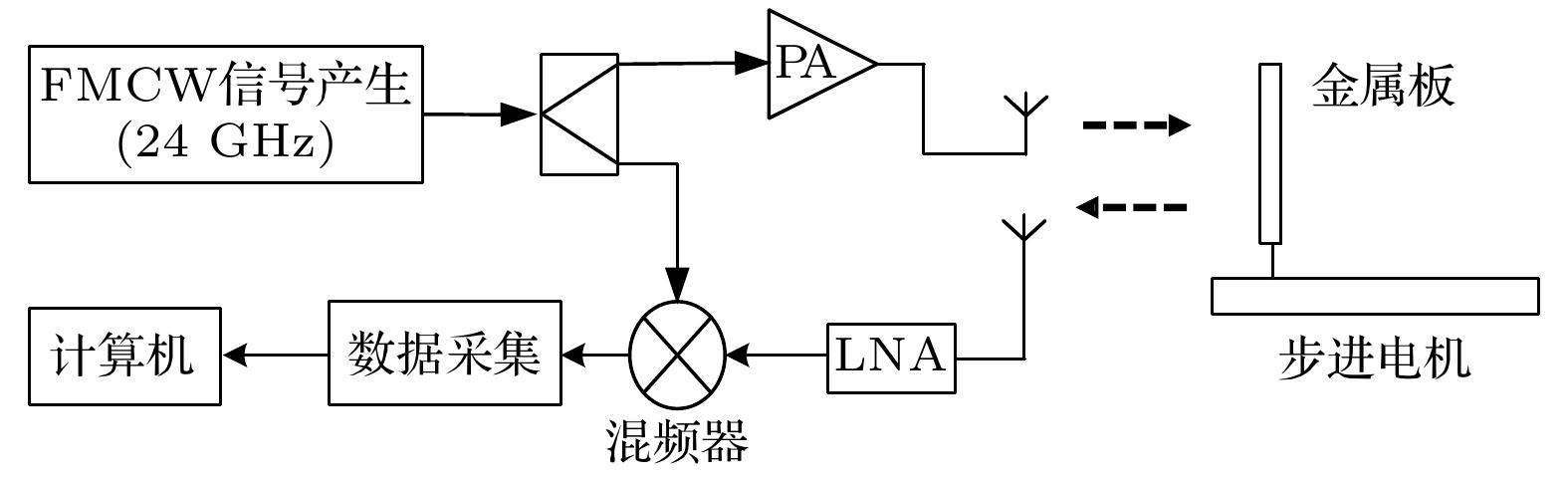
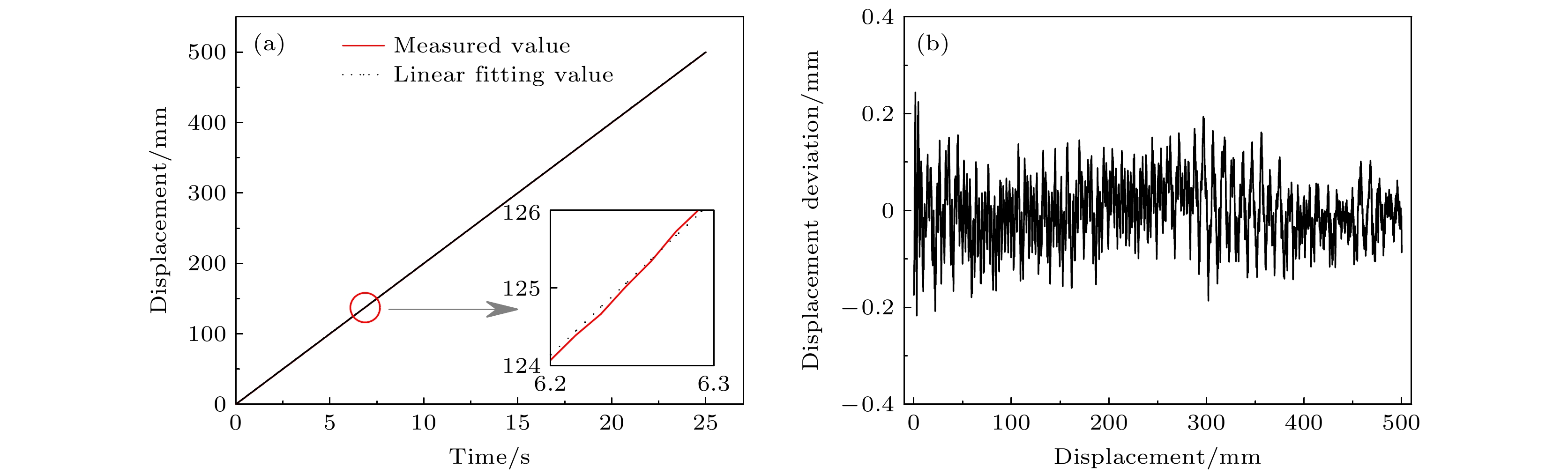
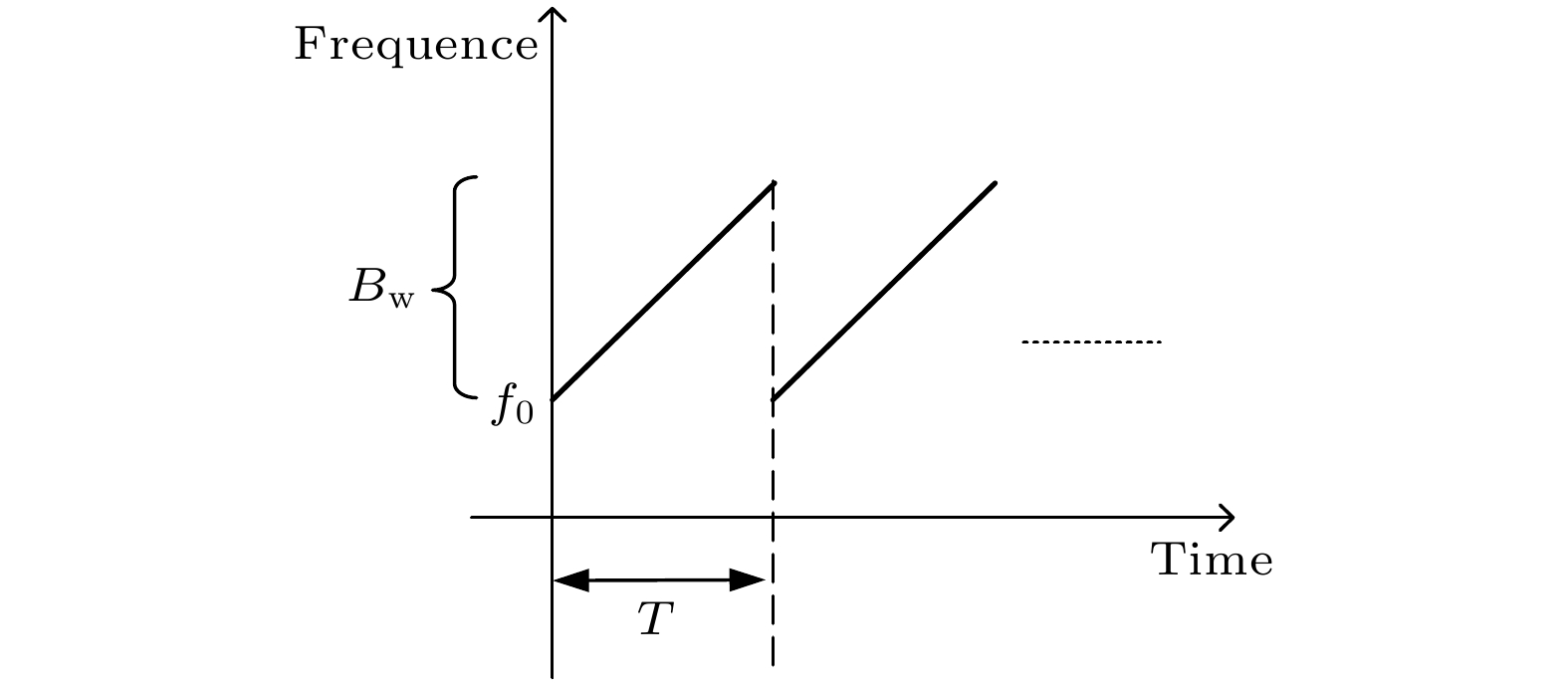
-
Real time detection of object motion is widely used in industrial activities and daily life. The contactless measurement is a flexible way, which has no effect on the state of movement of the object. Compared with the optical, ultrasonic and laser sensors, microwave radar has the advantages of high measurement accuracy and being unaffected by the environment such as smoke, dust, fog, and rain. The frequency modulated continuous wave (FMCW) radar is a widely used radar system, the echo of which contains abundant information, and there is no blind zone in the range because the transmitter and receiver work at the same time. The algorithm of movement detection of FMCW radar is commonly based on the peak estimation of signal spectrum, in order to achieve high accuracy, it is necessary to increase the frequency and bandwidth, resulting in high hardware complexity, a large amount of calculation, poor real-time response and poor anti-jamming ability. The proposed algorithm is based on the discrete Fourier transform with specific frequency of the beat signal. The real part and imaginary part of discrete Fourier transform are superposed in two perpendicular directions, and the resultant trajectory is approximately elliptical. The relative displacement of the object is proportional to the cumulative phase change of the corresponding points on the ellipse, the phase of each trajectory point can be calculated to restore the motion state of the object. The proposed algorithm does not need Fourier transform for the beat signal of each chirp, so the time complexity is low. The beat signal of the static object is processed into a fixed direct-current signal, which has no influence on the measurement of the moving object, therefore the algorithm has the ability to resist the interference of the static object. The measurement is limited to relative motion, because the phase obtained is relative. It has great potential applications in the fields of measuring relative displacement, such as mechanical vibration frequency, vital signal detection, mechanical arm control, etc.. An experimental setup with a center frequency of 24 GHz, bandwidth of 0.15 GHz and frequency modulation period of 4 ms is used to test the hypothesis. The experimental results are in good agreement with the theoretical results. The displacement measurement accuracy is 0.27 mm, and the linearity is 0.05% with 500 mm as the displacement measurement range. The measurement accuracy of velocity is 1.11 mm/s. -
Keywords:
- microwave /
- Frequency Modulated Continuous Wave radar /
- motion detection /
- synthetic trajectory
[1] Yang L, Wang B Q, Zhang R H, Zhou H B, Wang R B 2018 IEEE Photonics J 10 1
Google Scholar
[2] Yoon J W, Park T 2016 IEEE Trans. Instrum. Meas. 65 1518
Google Scholar
[3] 谢田元, 王菊, 王子雄, 马闯, 于洋, 李天宇, 方杰, 于晋龙 2019 68 130601
Google Scholar
Xie T Y, Wang J, Wang Z X, Ma C, Yu Y, Li T Y, Fang J, Yu J L 2019 Acta Phys. Sin. 68 130601
Google Scholar
[4] Kim S, Cam, Nguyen C 2003 IEEE Trans. Microw. Theory Tech. 51 1724
Google Scholar
[5] Kim D K, Kim Y 2019 Sci. Rep. 9 6763
Google Scholar
[6] Tudose M L, Anghel A, Cacoveanu R, Datcu M 2018 Sensors 19 82
Google Scholar
[7] Pittella E, Nasr I, Pisa S, Cavagnaro M 2016 IEEE Trans. Biomed. Eng. 63 1447
Google Scholar
[8] Mercuri M, Lorato I R, Liu Y H, Wieringa F, Hoof C V, Torfs T 2019 Nat. Electron. 2 252
Google Scholar
[9] Pan X, Xiang C, Liu S, Yan S 2019 Sensors 19 3176
Google Scholar
[10] Nosrati M, Shahsavari S, Lee S, Wang H, Tavassolian N 2019 IEEE Trans. Antennas Propag. 67 2390
Google Scholar
[11] Wang G C, Gu C Z, Inoue T, Li C Z 2014 IEEE Trans. Microw. Theory Tech. 62 2812
Google Scholar
[12] Schleicher B, Nasr I, Trasser A, Schumacher H 2013 IEEE Trans. Microw. Theory Tech. 61 2076
Google Scholar
[13] Qi G Q 2002 International Conference on Signal Processing Beijing, China, October 18–18, p7.
[14] Qi G Q, Jia X L 2001 CIE International Conference on Radar Proceedings Beijing, China, February 1–1, p567
[15] Pauli M, Ayhan S, Scherr S, Rusch C, Zwick T 2012 International Multi-conference on Systems Chemnitz, Germany, March 1–1, 2012 p4
[16] Scherr S, Ayhan S, Fischbach B, Bhutani A, Pauli M, Zwick T 2015 IEEE Trans. Instrum. Meas. 64 1868
Google Scholar
[17] Pauli M, Gottel B, Scherr S, Bhutani A, Ayhan S, Winkler W, Zwick T 2017 IEEE Trans. Microw. Theory Tech. 65 1707
Google Scholar
[18] Pohl N, Jaeschke T, Aufinger K 2012 IEEE Trans. Microw. Theory Tech. 60 757
Google Scholar
[19] Scherr S, Afroz R, Ayhan S, Thomas S, Jaeschke T, Marahrens S, Bhutani A, Pauli M, Pohl N, Zwick T 2017 IEEE Trans. Microw. Theory Tech. 65 3640
Google Scholar
[20] Piotrowsky L, Jaeschke T, Kueppers S, Siska J, Pohl N 2019 IEEE Trans. Microw. Theory Tech. 67 5360
Google Scholar
[21] Bredendiek C, Pohl N, Jaeschke T, Thomas S, Aufinger K, Bilgic A 2013 European Microwave Integrated Circuit Conference Amsterdam, Netherlands, October 29–30 2012 p309
[22] Jaeschke T, Bredendiek C, Kuppers S, Pohl N 2014 IEEE Trans. Microw. Theory Tech. 62 3582
Google Scholar
[23] 科尔曼T H 著 (殷建平 译) 2013 算法导论 (北京: 机械工业出版社) 第25−29页
Cormen T H (translated by Yin J P) 2013 Introduction to Algorithms (Beijing: Machinery Industry Press) pp25−29 (in Chinese)
-
图 1 发射波的频率随时间的变化
Figure 1. the time-frequency domain of transmitted signal.
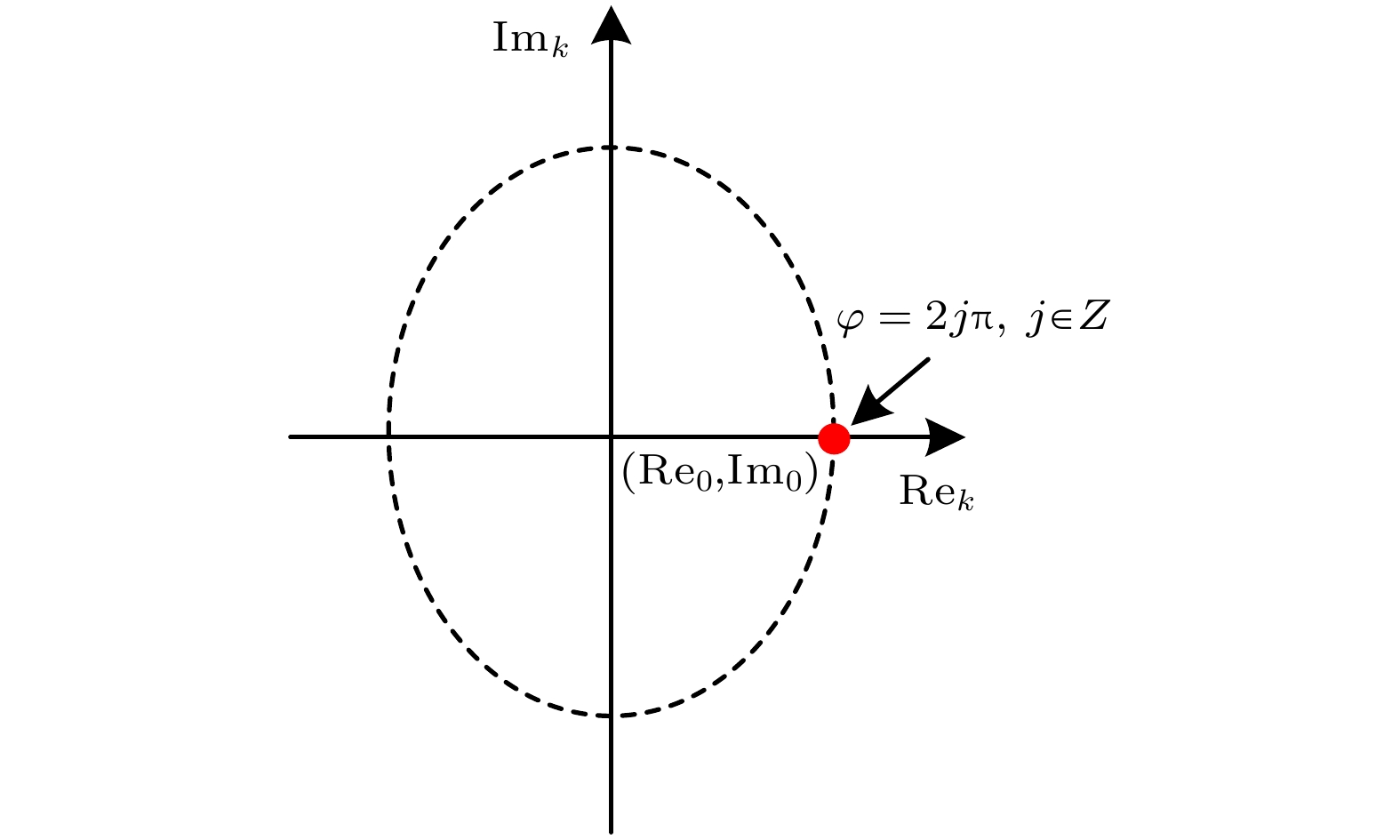
图 2 变量
$ {\rm{Re}}_{{k}} $ 和$ {\rm{Im}}_{{k}} $ 的合成轨迹示意图. 红色实心点处在横坐标轴的正半轴上, 代表相位φ = 2jπ, j∈Z的位置Figure 2. The synthetic ellipse trajectory diagram of variables
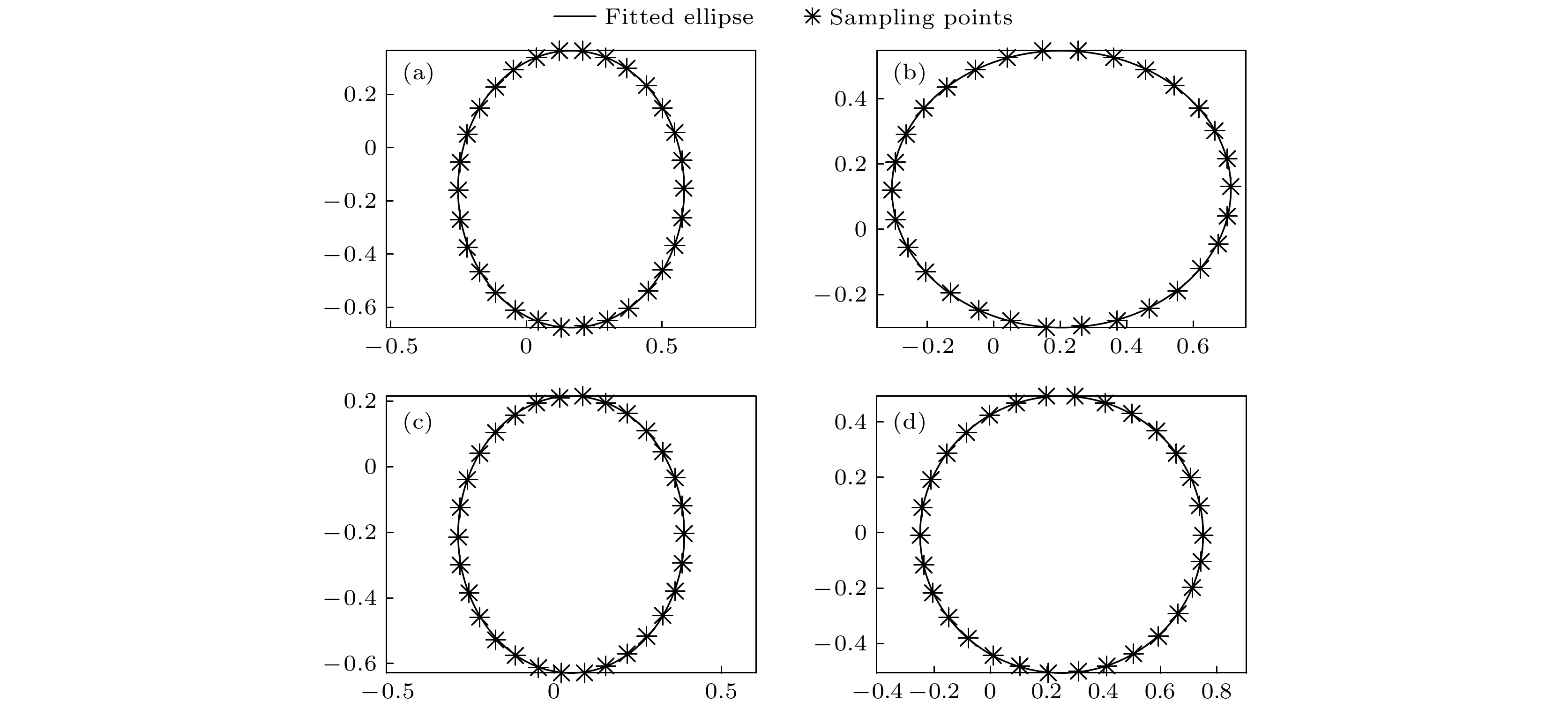
$ {\rm{Re}}_{{k}} $ and$ {\rm{Im}}_{{k}} $ . The red solid point is on the positive half axis of abscissa, which represents the position of φ = 2jπ, j∈Z.
图 3 雷达前端 (a)正面为收发天线; (b)反面为电路板
Figure 3. Radar front end: (a) The front side is transceiver antenna; (b) the reverse side is circuit board.
图 4 实验系统结构图
Figure 4. Block diagram of the FMCW radar system.
图 5 测量装置与载有金属板的步进电机
Figure 5. Measuring set and stepper motor with metal plate.
图 6 计算机模拟在4种不同起始距离下做
$ \lambda /2 $ 位移时的采样点轨迹变化, 起始距离分别为 (a) 800 mm; (b) 1200 mm; (c) 1600 mm; (d) 2000 mmFigure 6. Computer simulation of trajectory change by these sampling points at four different starting distances, the displacement is
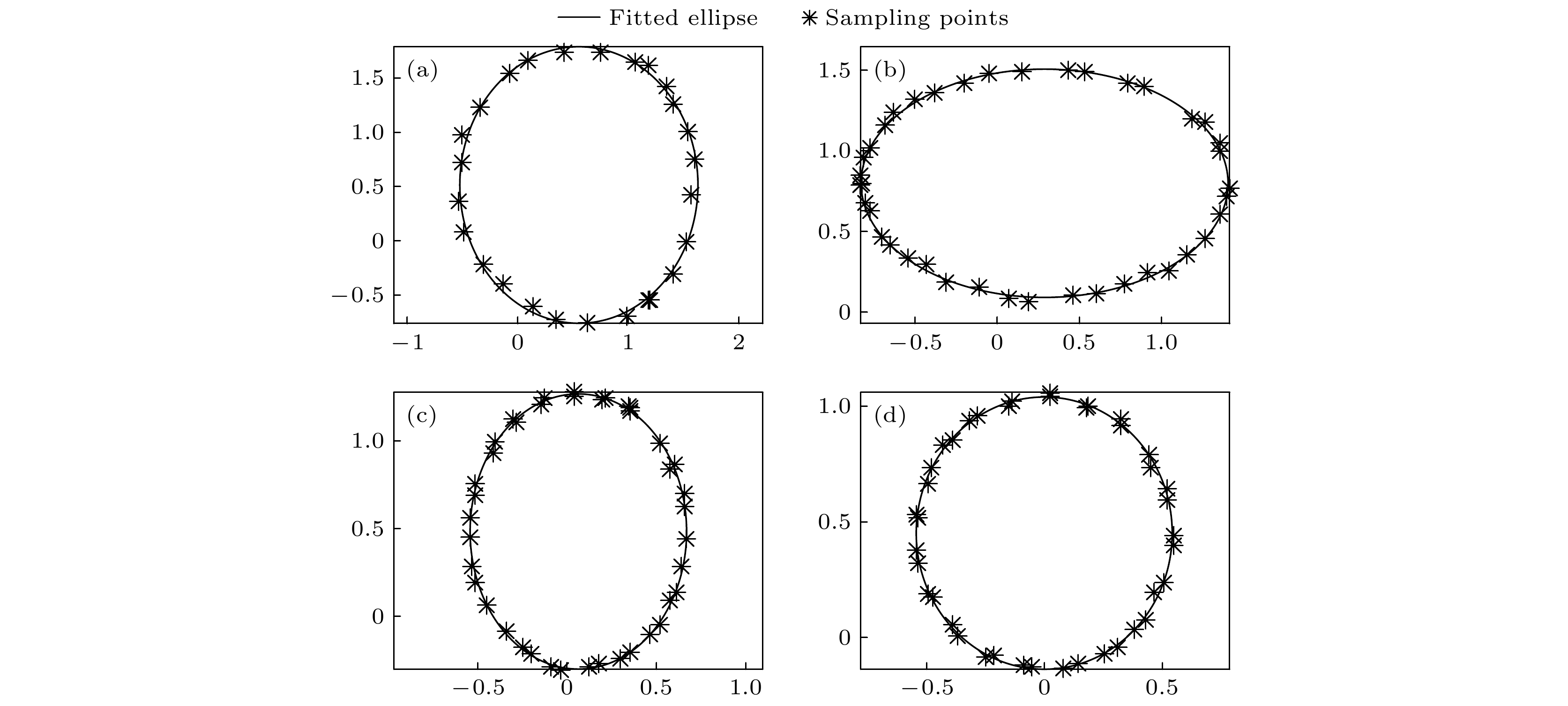
$ \lambda /2 $ , the starting distances are: (a) 800 mm; (b) 1200 mm; (c) 1600 mm; (d) 2000 mm.
图 7 实验测量在4种不同起始距离下做
$ \lambda /2 $ 位移时的采样点轨迹变化, 起始距离分别为 (a) 800 mm; (b) 1200 mm; (c) 1600 mm; (d) 2000 mmFigure 7. Experimental measurement of trajectory changes by these sampling points at four different starting distances, the displacement is
$ \lambda /2 $ , the starting distances are: (a) 800 mm; (b) 1200 mm; (c) 1600 mm; (d) 2000 mm.
图 8 位移测量结果 (a)位移随时间的变化; (b)位移偏差随位移的变化
Figure 8. Measurement of displacement of metal plate: (a) Change of displacement with time; (b) change of displacement deviation.
图 9 (a)测量位移和设定位移的比较; (b)测量位移的偏差变化
Figure 9. (a) Change of measured displacement and set displacement with time; (b) deviation of measured displacement.
图 10 (a)速度测量值和速度设定值的比较; (b)速度测量值的偏差变化
Figure 10. (a) Change of measured speed and set speed with time; (b) deviation of measured speed.
表 1 与其他算法的比较
Table 1. Comparison of this work with other methods.
文献 算法 时间复杂度* 测量环境 测量内容 [21] 插值法 O($N{\,\mathrm{l}\mathrm{o}\mathrm{g} }_{2}N$) 环境简单, 被测物几乎是唯一的散射源 绝对距离 [22] 补零法 O($M \log_{2}M$) 绝对距离 [19] CZT O($N\log_{2}N$)+ O($ {N}^{3/2} $) 绝对距离 [20] 插值法+补零法 O($M\log_{2}M$) 绝对距离 [16] CZT O($N\log_2 N$)+ O($ {N}^{3/2} $) 被测物及雷达封装在波导内 绝对距离 本算法 O(N) 无其他运动物体 相对距离 注: *N 为一个调频周期内拍信号的采样点数目. M 为补零后的采样点数目. 
DownLoad: CSV
表 2 金属板运动的测量结果
Table 2. Measurement results of metal plate movement.
设定速度
/(mm·s–1)位移设
定值/mm位移测量值 平均
值/mm平均值的
偏差/mm最大
偏差/mm标准
差/mm10 300 300.10 0.10 0.26 0.15 400 399.91 –0.09 0.24 0.15 500 499.93 –0.07 0.25 0.14 20 300 299.95 –0.05 0.21 0.12 400 400.08 0.08 0.24 0.14 500 500.05 0.05 0.27 0.13 30 300 300.09 0.09 0.26 0.15 400 399.96 –0.04 0.21 0.12 500 499.96 –0.04 0.23 0.12
DownLoad: CSV
-
[1] Yang L, Wang B Q, Zhang R H, Zhou H B, Wang R B 2018 IEEE Photonics J 10 1
Google Scholar
[2] Yoon J W, Park T 2016 IEEE Trans. Instrum. Meas. 65 1518
Google Scholar
[3] 谢田元, 王菊, 王子雄, 马闯, 于洋, 李天宇, 方杰, 于晋龙 2019 68 130601
Google Scholar
Xie T Y, Wang J, Wang Z X, Ma C, Yu Y, Li T Y, Fang J, Yu J L 2019 Acta Phys. Sin. 68 130601
Google Scholar
[4] Kim S, Cam, Nguyen C 2003 IEEE Trans. Microw. Theory Tech. 51 1724
Google Scholar
[5] Kim D K, Kim Y 2019 Sci. Rep. 9 6763
Google Scholar
[6] Tudose M L, Anghel A, Cacoveanu R, Datcu M 2018 Sensors 19 82
Google Scholar
[7] Pittella E, Nasr I, Pisa S, Cavagnaro M 2016 IEEE Trans. Biomed. Eng. 63 1447
Google Scholar
[8] Mercuri M, Lorato I R, Liu Y H, Wieringa F, Hoof C V, Torfs T 2019 Nat. Electron. 2 252
Google Scholar
[9] Pan X, Xiang C, Liu S, Yan S 2019 Sensors 19 3176
Google Scholar
[10] Nosrati M, Shahsavari S, Lee S, Wang H, Tavassolian N 2019 IEEE Trans. Antennas Propag. 67 2390
Google Scholar
[11] Wang G C, Gu C Z, Inoue T, Li C Z 2014 IEEE Trans. Microw. Theory Tech. 62 2812
Google Scholar
[12] Schleicher B, Nasr I, Trasser A, Schumacher H 2013 IEEE Trans. Microw. Theory Tech. 61 2076
Google Scholar
[13] Qi G Q 2002 International Conference on Signal Processing Beijing, China, October 18–18, p7.
[14] Qi G Q, Jia X L 2001 CIE International Conference on Radar Proceedings Beijing, China, February 1–1, p567
[15] Pauli M, Ayhan S, Scherr S, Rusch C, Zwick T 2012 International Multi-conference on Systems Chemnitz, Germany, March 1–1, 2012 p4
[16] Scherr S, Ayhan S, Fischbach B, Bhutani A, Pauli M, Zwick T 2015 IEEE Trans. Instrum. Meas. 64 1868
Google Scholar
[17] Pauli M, Gottel B, Scherr S, Bhutani A, Ayhan S, Winkler W, Zwick T 2017 IEEE Trans. Microw. Theory Tech. 65 1707
Google Scholar
[18] Pohl N, Jaeschke T, Aufinger K 2012 IEEE Trans. Microw. Theory Tech. 60 757
Google Scholar
[19] Scherr S, Afroz R, Ayhan S, Thomas S, Jaeschke T, Marahrens S, Bhutani A, Pauli M, Pohl N, Zwick T 2017 IEEE Trans. Microw. Theory Tech. 65 3640
Google Scholar
[20] Piotrowsky L, Jaeschke T, Kueppers S, Siska J, Pohl N 2019 IEEE Trans. Microw. Theory Tech. 67 5360
Google Scholar
[21] Bredendiek C, Pohl N, Jaeschke T, Thomas S, Aufinger K, Bilgic A 2013 European Microwave Integrated Circuit Conference Amsterdam, Netherlands, October 29–30 2012 p309
[22] Jaeschke T, Bredendiek C, Kuppers S, Pohl N 2014 IEEE Trans. Microw. Theory Tech. 62 3582
Google Scholar
[23] 科尔曼T H 著 (殷建平 译) 2013 算法导论 (北京: 机械工业出版社) 第25−29页
Cormen T H (translated by Yin J P) 2013 Introduction to Algorithms (Beijing: Machinery Industry Press) pp25−29 (in Chinese)
DownLoad:
Catalog
Metrics
- Abstract views: 5332
- PDF Downloads: 104
- Cited By: 0
