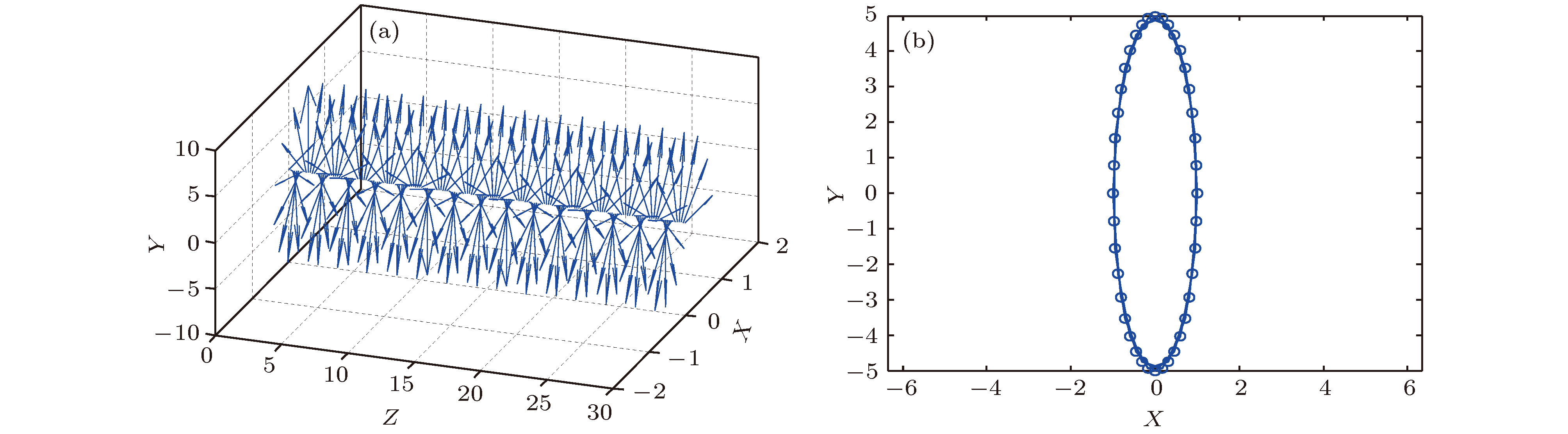
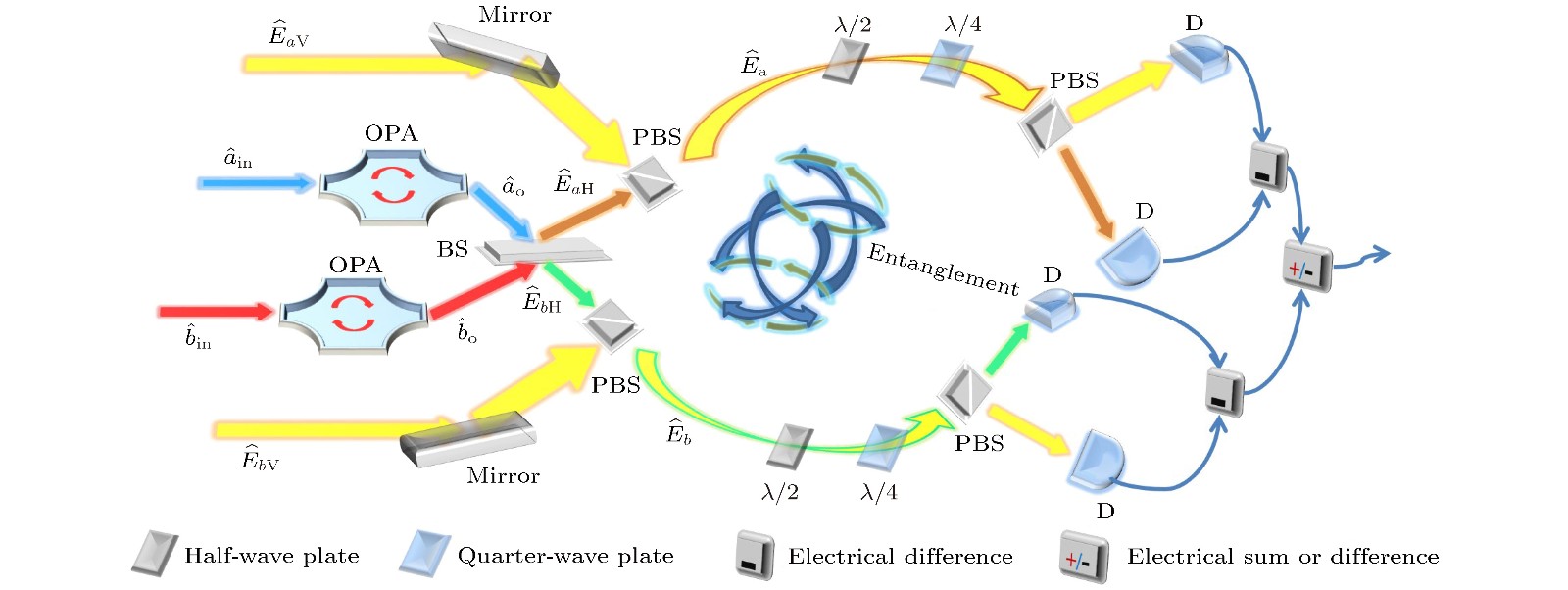
-
As a widely utilized information carrier, polarization microwave shows plenty of merits. Quantum microwave is booming gradually due to the development of superconducting technology, which makes it a promising potential to apply quantum entanglement to polarization microwave. In this paper, we introduce the concept of continuous variable polarization entanglement. Meanwhile, a scheme of polarization entanglement in microwave domain is proposed and simulated. The detail derivations are given and discussed. Polarization entangled microwaves are prepared by combining quadrature entangled signals and strong coherent signals on polarization beam splitters, and quadrature entangled signals are prepared by utilizing Josephson mixer. In order to probe the polarization entanglement between output signals, inseparability of Stokes vectors
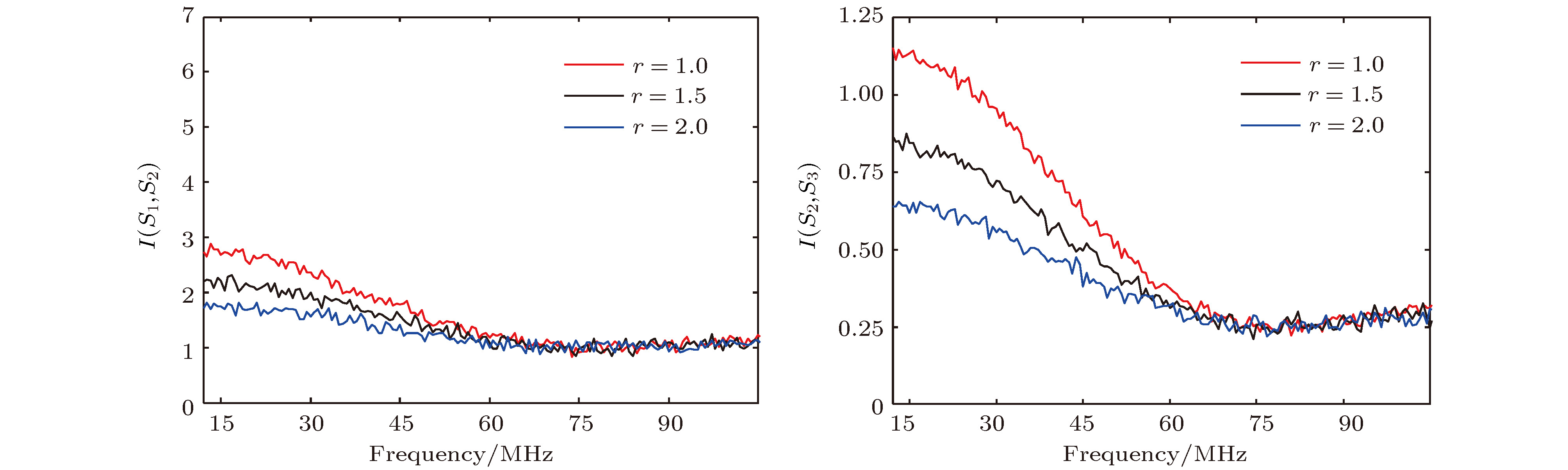
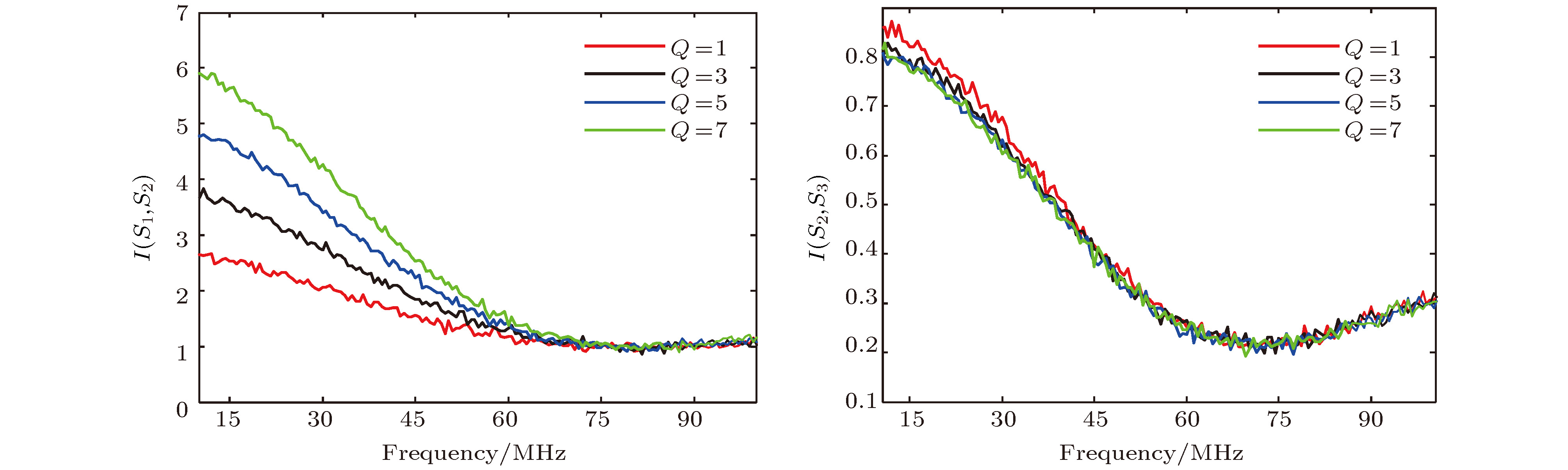
$I({\hat S_1},{\hat S_2})$ and$I({\hat S_2},{\hat S_3})$ , is analyzed in 100 MHz operation bandwidth of Josephson mixer. The relation between inseparability I and squeezing degree r and between inseparability I and amplitude ratio Q are analyzed respectively. The results show that$I({\hat S_1},{\hat S_2})$ is sensitive to the variation of Q, while$I({\hat S_2},{\hat S_3})$ is sensitive to the change of r. The physical reasons for these results are explored and discussed. Apart from these,$I({\hat S_1},{\hat S_2})$ remains its value above 1 under the condition in this paper, but on the contrary,$I({\hat S_2},{\hat S_3})$ keeps its value well below 1. It proves that${\hat S_2}$ and${\hat S_3}$ of Stokes vectors are inseparable from each other, thus output signals${\hat E_a}$ and${\hat E_b}$ of our scheme exhibit bipartite entanglement. The best entanglement appears nearly at about 70 MHz, at this point the minimum$I({\hat S_2},{\hat S_3})$ value is 0.25.-
Keywords:
- continuous variable /
- polarization entanglement /
- Josephson mixer /
- Stokes vectors /
- inseparability
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[2] Liu C C, Wang D, Sun W Y, Ye L 2017 Quantum Inf. Process. 16 219
Google Scholar
[3] Ourjoumtsev A 2010 Nat. Photon. 4 136
Google Scholar
[4] Bowen W P, Treps N, Schnabel R, Ralph T C, Lam P K 2003 J. Opt. B: Quantum Semiclassical Opt. 5 s467
Google Scholar
[5] Zhou L, Ou-Yang Y, Wang L, Sheng Y B 2017 Quantum Inf. Process. 16 151
Google Scholar
[6] Bowen W P, Treps N, Schnabel R, Lam P K 2002 Phys. Rev. Lett. 89 253601
Google Scholar
[7] Korolkova N, Leuchs G, Loudon R, Ralph T C, Silberhorn C 2002 Phys. Rev. A 65 052306
Google Scholar
[8] Guo J, Cai C X, Ma L, Liu K, Sun H X, Gao J R 2017 Sci. Rep. 7 4434
Google Scholar
[9] 吴量, 刘艳红, 邓瑞婕, 闫智辉, 贾晓军 2017 光学学报 5 0527001
Wu L, Liu Y H, Deng R J, Yan Z H, Jia X J 2017 Acta Opt. Sin. 5 0527001
[10] Wu L, Yan Z H, Liu Y H, Deng R J, Jia X J, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 161102
Google Scholar
[11] 周瑶瑶, 蔚娟, 闫智辉, 贾晓军 2018 光学学报 7 0727001
Zhou Y Y, Yu J, Yan Z H, Jia X J 2018 Acta Opt. Sin. 7 0727001
[12] Chen Y F, Hover D, Sendelbach S, Maurer L N 2011 Phys. Rev. Lett. 107 217401
Google Scholar
[13] Hofheinz M, Huard B, Portier F 2016 C. R. Phys. 17 679
Google Scholar
[14] Flurin E, Roch N, Mallet F, Devoret M H, Huard B 2012 Phys. Rev. Lett. 109 183901
Google Scholar
[15] Roch N, Flurin E, Nguyen F, Morfin P, Campagne-Ibarcq P, Devoret M H, Huard B 2012 Phys. Rev. Lett. 108 147701
Google Scholar
[16] Flurin E, Roch N, Pillet J D, Mallet F, Huard B 2015 Phys. Rev. Lett. 114 090503
Google Scholar
[17] Robson B A 1974 The Theory of Polarization Phenomena (Oxford: Clarendon)
[18] Christopher S R 1998 Radio Sci. 33 1617
Google Scholar
[19] Duan L M, Giedke G, Cirac J I, Zoller P 2000 Phys. Rev. Lett. 84 2722
Google Scholar
[20] Flurin E 2014 Ph. D. Dissertation (Berkeley: University of California)
[21] Sneep J G, Verhoeven C J M 1990 IEEE J. Solid-State Circuits 25 692
Google Scholar
-
图 1 两组分极化纠缠光场生成及探测原理图(OPA, 光参量放大器; BS, 分束器; PBS, 极化分束器; D, 探测器)
Figure 1. Scheme of preparation and measurement towards bipartite polarization entangled optical fields. OPA, optical parametric amplifier; BS, beam splitter; PBS, polarization beam splitter; D, detector.
图 2 二组分极化纠缠微波方案示意图(D, 探测器; 方案整体工作温度为0.5 mK)
Figure 2. Schematic of bipartite polarization entangled microwave. D, detector. Overall operation temperature of the proposal is 0.5 mK
图 3
${{\hat{E}}_{a{\rm{H}}}}$ ,${{\hat{E}}_{b{\rm{H}}}}$ 的正交分量间的时域关联 (a)振幅分量XH; (b)相位分量YHFigure 3. Quadrature components correlations of
${{\hat{E}}_{a{\rm{H}}}}$ and${{\hat{E}}_{b{\rm{H}}}}$ in time domain: (a) Amplitude component XH; (b) phase component YH
图 4 合成信号传输过程电场状态(a)和矢端轨迹(b)
Figure 4. Electric field state (a) and vector end trajectory (b) of combined signal in transmission.
图 5
${{\hat{E}}_a}$ ,${{\hat{E}}_b}$ 对应斯托克斯参量的起伏关系Figure 5. Fluctuations correlation of corresponding Stokes vectors between
${{\hat{E}}_a}$ and${{\hat{E}}_b}$ .
图 6 不可分度I与压缩度r的关系 (a)
$I\left( {\hat {{S_1}}, \hat {{S_2}}} \right)$ ; (b)$I\left( {\hat {{S_2}}, \hat {{S_3}}} \right)$ Figure 6. Relations of inseparability I and squeezing degree r : (a)
$I\left( {\widehat {{S_1}}, \hat {{S_2}}} \right)$ ; (b)$I\left( {\hat {{S_2}}, \hat {{S_3}}} \right)$ .
图 7 不可分度I与振幅比值Q的关系 (a)
$I\left( {\hat {{S_1}}, \hat {{S_2}}} \right)$ ; (b)$I\left( {\hat {{S_2}}, \hat {{S_3}}} \right)$ .Figure 7. Relations of inseparability I and amplitude ratio Q : (a)
$I\left( {\hat {{S_1}}, \hat {{S_2}}} \right)$ ; (b)$I\left( {\hat {{S_2}}, \hat {{S_3}}} \right)$ .表 1 方案部分参数
Table 1. Part of the parameters in the scheme.
参数
名称输入信号
频率/GHz输入信号
振幅压缩参量 r 极化分量
振幅比值 Q参数值 5 1 2 5 
DownLoad: CSV
-
[1] Einstein A, Podolsky B, Rosen N 1935 Phys. Rev. 47 777
Google Scholar
[2] Liu C C, Wang D, Sun W Y, Ye L 2017 Quantum Inf. Process. 16 219
Google Scholar
[3] Ourjoumtsev A 2010 Nat. Photon. 4 136
Google Scholar
[4] Bowen W P, Treps N, Schnabel R, Ralph T C, Lam P K 2003 J. Opt. B: Quantum Semiclassical Opt. 5 s467
Google Scholar
[5] Zhou L, Ou-Yang Y, Wang L, Sheng Y B 2017 Quantum Inf. Process. 16 151
Google Scholar
[6] Bowen W P, Treps N, Schnabel R, Lam P K 2002 Phys. Rev. Lett. 89 253601
Google Scholar
[7] Korolkova N, Leuchs G, Loudon R, Ralph T C, Silberhorn C 2002 Phys. Rev. A 65 052306
Google Scholar
[8] Guo J, Cai C X, Ma L, Liu K, Sun H X, Gao J R 2017 Sci. Rep. 7 4434
Google Scholar
[9] 吴量, 刘艳红, 邓瑞婕, 闫智辉, 贾晓军 2017 光学学报 5 0527001
Wu L, Liu Y H, Deng R J, Yan Z H, Jia X J 2017 Acta Opt. Sin. 5 0527001
[10] Wu L, Yan Z H, Liu Y H, Deng R J, Jia X J, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 161102
Google Scholar
[11] 周瑶瑶, 蔚娟, 闫智辉, 贾晓军 2018 光学学报 7 0727001
Zhou Y Y, Yu J, Yan Z H, Jia X J 2018 Acta Opt. Sin. 7 0727001
[12] Chen Y F, Hover D, Sendelbach S, Maurer L N 2011 Phys. Rev. Lett. 107 217401
Google Scholar
[13] Hofheinz M, Huard B, Portier F 2016 C. R. Phys. 17 679
Google Scholar
[14] Flurin E, Roch N, Mallet F, Devoret M H, Huard B 2012 Phys. Rev. Lett. 109 183901
Google Scholar
[15] Roch N, Flurin E, Nguyen F, Morfin P, Campagne-Ibarcq P, Devoret M H, Huard B 2012 Phys. Rev. Lett. 108 147701
Google Scholar
[16] Flurin E, Roch N, Pillet J D, Mallet F, Huard B 2015 Phys. Rev. Lett. 114 090503
Google Scholar
[17] Robson B A 1974 The Theory of Polarization Phenomena (Oxford: Clarendon)
[18] Christopher S R 1998 Radio Sci. 33 1617
Google Scholar
[19] Duan L M, Giedke G, Cirac J I, Zoller P 2000 Phys. Rev. Lett. 84 2722
Google Scholar
[20] Flurin E 2014 Ph. D. Dissertation (Berkeley: University of California)
[21] Sneep J G, Verhoeven C J M 1990 IEEE J. Solid-State Circuits 25 692
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7325
- PDF Downloads: 58
- Cited By: 0
