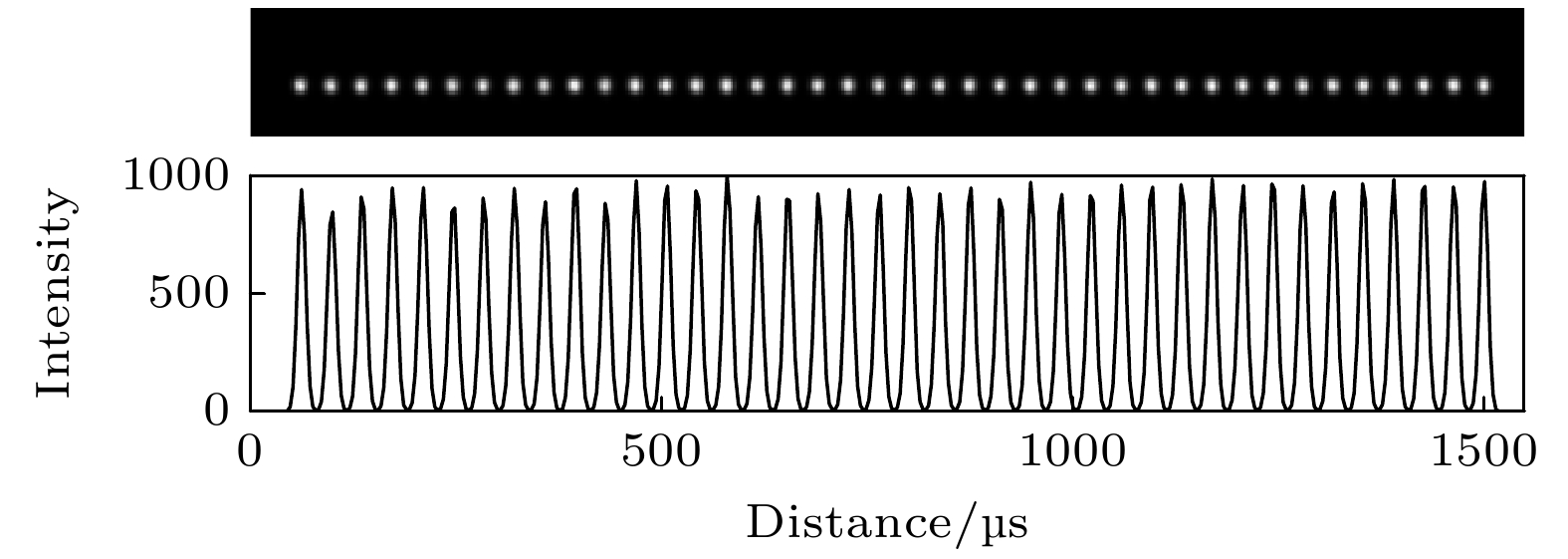
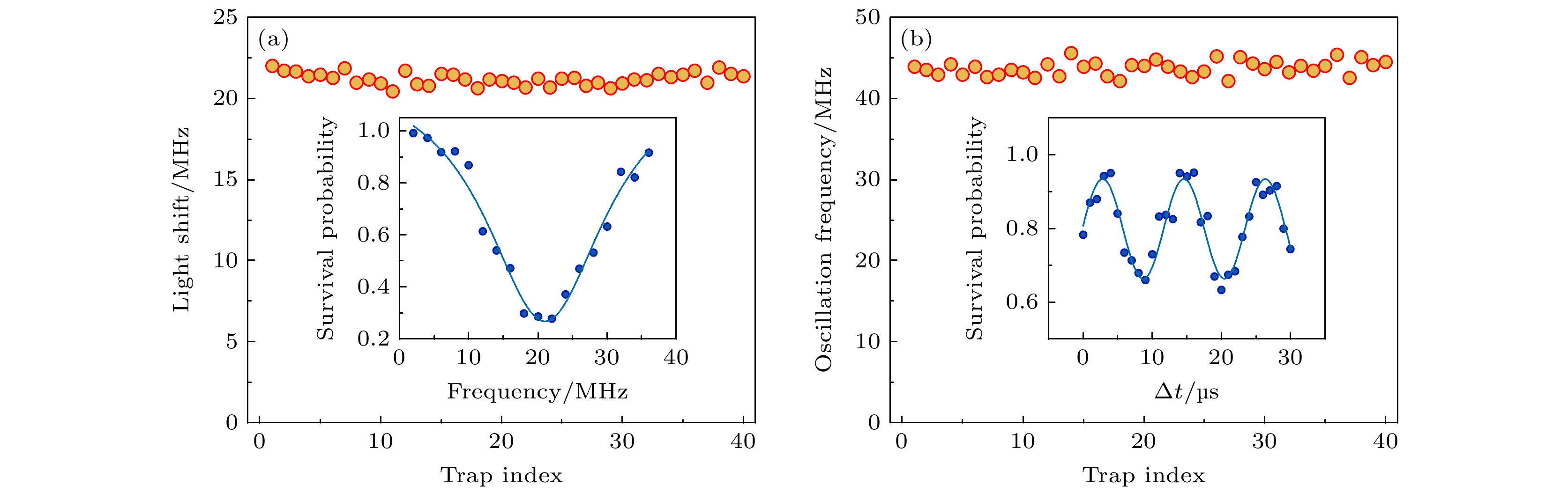
-
Neutral atom array serves as a crucial experimental platform for studying many-body physics, quantum computing, and quantum simulation. In this work, we describe in detail the experimental process of preparing a one-dimensional homogeneous single atom array containing 40 Cs atoms, including the dipole trap array generation device, atomic array fluorescence imaging, and the uniformity optimization of the dipole trap array. The beam waist of the dipole trap is about 1.8 μm, and the spatial resolution of the imaging system is higher than 1.55 μm. The non-uniformity of dipole trap array is mainly caused by the intermodulation effect of multi-tone signal during amplification. The uniformity of the dipole trap array is optimized to 2% (Fig. (a)) by measuring the fluctuations of the dipole trap intensity and the light shift of trapped atom, and providing feedback to adjust the phase and amplitude applied to the multi-tone RF signal on acousto-optic deflectors. Furthermore, the uniformity of oscillation frequency, loading rate, and lifetime for trapped atom in the dipole trap array are measured. These results show that oscillation frequency has a uniformity within 2% (Fig. (b)); mean loading rate is around 58% with a uniformity within 3%; and mean lifetime of single atom in dark trap is around 6(1) s with a uniformity within 8%.
-
Keywords:
- quantum computing /
- atom array /
- acousto-optic deflector /
- intermodulation
[1] Weiss D S, Saffman M 2017 Phys. Today 70 44
Google Scholar
[2] Bruzewicz C D, McConnell R, Chiaverini J, Sage J M 2016 Nat. Commun. 7 13005
Google Scholar
[3] Gong M, Chen M C, Zheng Y R, Wang S Y, Zha C, Deng H, Yan Z G, Rong H, Wu Y L, Li S W, Chen F S, Zhao Y W, Liang F T, Lin J, Xu Y, Guo C, Sun L H, Castellano A D, Wang H H, Peng C Z, Lu C Y, Zhu X B, Pan J W 2019 Phys. Rev. Lett. 122 110501
Google Scholar
[4] Singh K, Anand S, Pocklington A, Kemp J T, Bernien H 2022 Phy. Rev. X 12 011040
[5] Bernien H, Schwartz S, Keesling A, Levine H, Omran A, Pichler H, Choi S, Zibrov A S, Endres M, Vuletić V, Lukin M D 2017 Nature 551 579
Google Scholar
[6] Labuhn H, Barredo D, Ravets S, Léséleuc S D, Macrì T, Lahaye T, Browaeys A 2016 Nature 534 667
Google Scholar
[7] Ebadi S, Wang T T, Levine H, Keesling A, Semeghini G, Omran A, Bluvstein D, Samajdar R, Pichler H, Ho W W, Choi S, Sachdev S, Greiner M, Vladan Vuletić V, Lukin M D 2021 Nature 595 227
Google Scholar
[8] Scholl P, Schuler M, Williams H J, Eberharter A A, Barredo D, Schymik K N, Lienhard V, Henry L P, Lang T C, Lahaye T, Läuchli A M, Browaeys A 2021 Nature 595 233
Google Scholar
[9] Norcia M A, Cairncross W B, Barnes K, et al. 2023 Phys. Rew. X 13 041034
[10] Singh K, Bradley C E, Anand S, Ramesh V, White R, Bernien H 2023 Science 380 126
Google Scholar
[11] Evered S J, Bluvstein D, Kalinowski M, Ebadi S, Manovitz T, Zhou H, Li S H, Geim A A, Wang T T, Maskara N, Levine H, Semeghini G, Greiner M, Vuletic V, Lukin M D 2023 Nature 622 268
Google Scholar
[12] Graham T M, Song Y, Scott J, Poole C, Phuttitarn L, Jooya K, Eichler P, Jiang X, Marra A, Grinkemeyer B, Kwon M, Ebert M, Cherek J, Lichtman M T, Gillette M, Gilbert J, Bowman D, Ballance T, Campbell C, Dahl E D, Crawford O, Blunt N S, Rogers B, Noel T, Saffman M 2023 Nature 604 457
Google Scholar
[13] Bluvstein D, Evered S J, Geim A A, Li S H, Zhou H, Manovitz T, Ebadi S, Cain M, Kalinowski M, Hangleiter D, Ataides J P B, Maskara N, Cong I, Gao X, Rodriguez P S, Karolyshyn T, Semeghini G, Gullans M J, Greiner M, Vuletic V, Lukin M D 2024 Nature 626 58
Google Scholar
[14] Barredo D, De Léséleuc S, Lienhard V, Lahaye T, Browaeys A 2016 Science 354 1021
Google Scholar
[15] Endres M, Bernien H, Keesling A, Levine H, Anschuetz E R, Krajenbrink A, Lukin M D 2016 Science 354 1024
Google Scholar
[16] Brown M O, Thiele T, Kiehl C, Hsu T W, Regal C A 2019 Phys. Rev. X 9 011057
[17] Semeghini G, Levine H, Keesling A, Ebadi S, Wang T T, Bluvstein D, Verresen R, Pichler H, Kalinowski M, Lukin M D 2021 Science 374 1242
Google Scholar
[18] Sergi J F, Joseph V, Alexandre D 2024 arXiv: 2402.02852 [cond-mat.quant-gas]
[19] Liu Y X, Wang Z H, Yang P F, Wang Q X, Fan Q, Guan S J, Li G, Zhang P F, Zhang T C 2023 Phys. Rev. Lett. 130 173601
Google Scholar
[20] Deist E, Gerber J A, Lu Y H, Zeiher J, Stamper-Kurn D M 2022 Phys. Rev. Lett. 128 083201
Google Scholar
[21] Ðorđević T, Samutpraphoot P, Ocola P L, Bernien H, Grinkemeyer B, Dimitrova I, Vuletić V, Lukin M D 2021 Science 373 1511
Google Scholar
[22] Deist E, Lu Y H, Ho J, Pasha M K, Zeiher J, Yan Z, Stamper-Kurn D M 2022 Phys. Rev. Lett. 129 203602
Google Scholar
[23] Yan Z J, Jacquelyn H, Lu Y H, Masson S J, Asenjo-Garcia A, Stamper-Kurn D M 2023 Phys. Rev. Lett. 131 253603
Google Scholar
[24] Li S K, Li G, Wu W, Fan Q, TianY L, Yang P F, Zhang P F, Zhang T C 2020 Rev. Sci. Instrum. 91 043104
Google Scholar
[25] Schlosser N, Reymond G, Grangier P 2002 Phys. Rev. Lett. 89 023005
Google Scholar
[26] Sortais Y R P, Marion H, Tuchendler C, Lance A M, Lamare M, Fournet P, Armellin C, Mercier R, Messin G, Browaeys A, Grangier P 2007 Phys. Rev. A 75 013406
Google Scholar
[27] Sheng C, He X, Xu P, Guo R, Wang K, Xiong Z, Liu M, Wang J, Zhan M 2018 Phys. Rev. Lett. 121 240501
Google Scholar
-
图 1 偶极阱阵列以及成像光路示意图, 插图为AOD工作原理示意图
Figure 1. Schematic diagram of the dipole trap array and imaging optics, and the inset demonstrates the operational principle of AOD.
图 2 偶极阱阵列CCD成像图及强度分布
Figure 2. CCD imaging and intensity distribution of the dipole trap array.
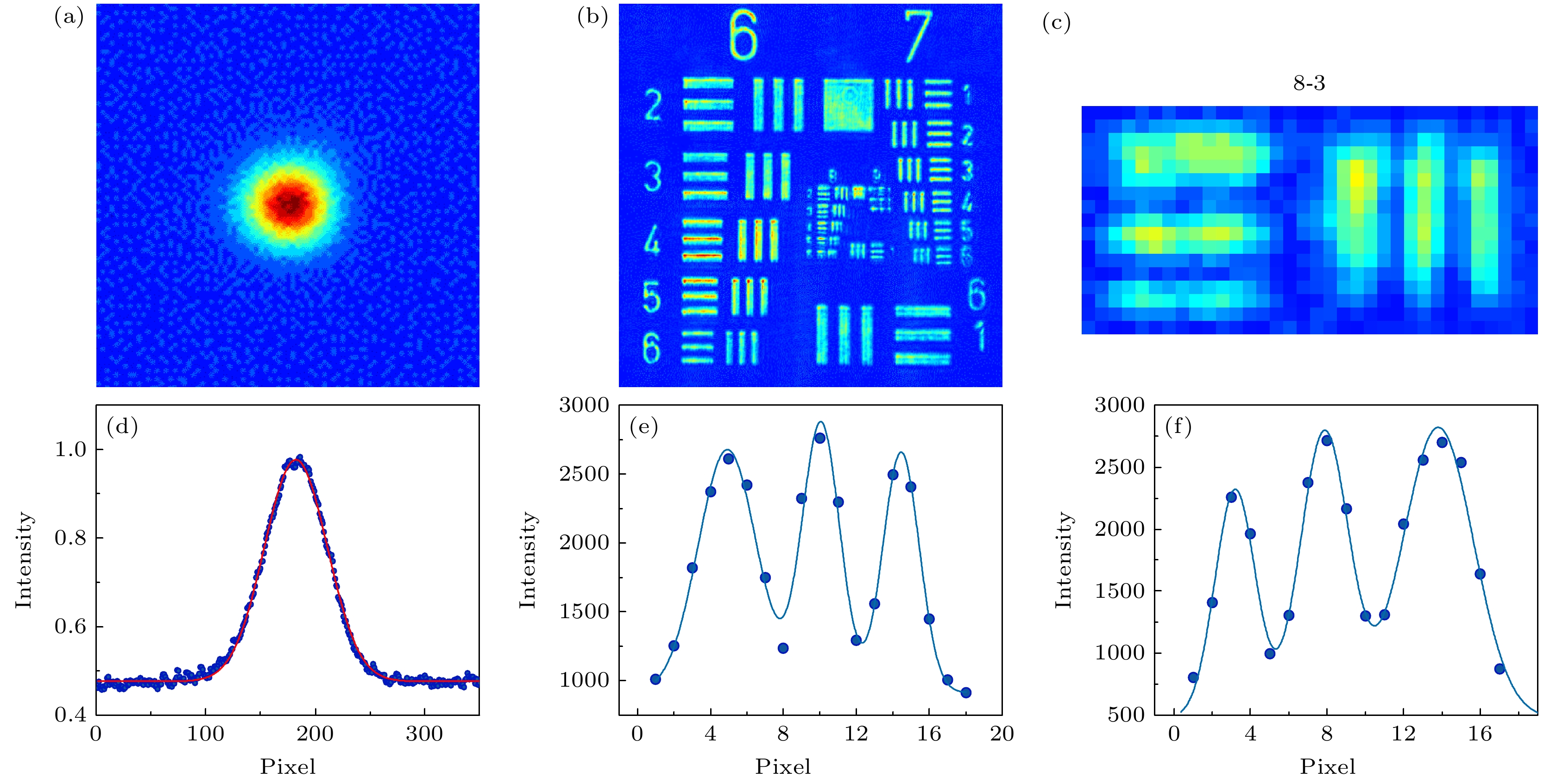
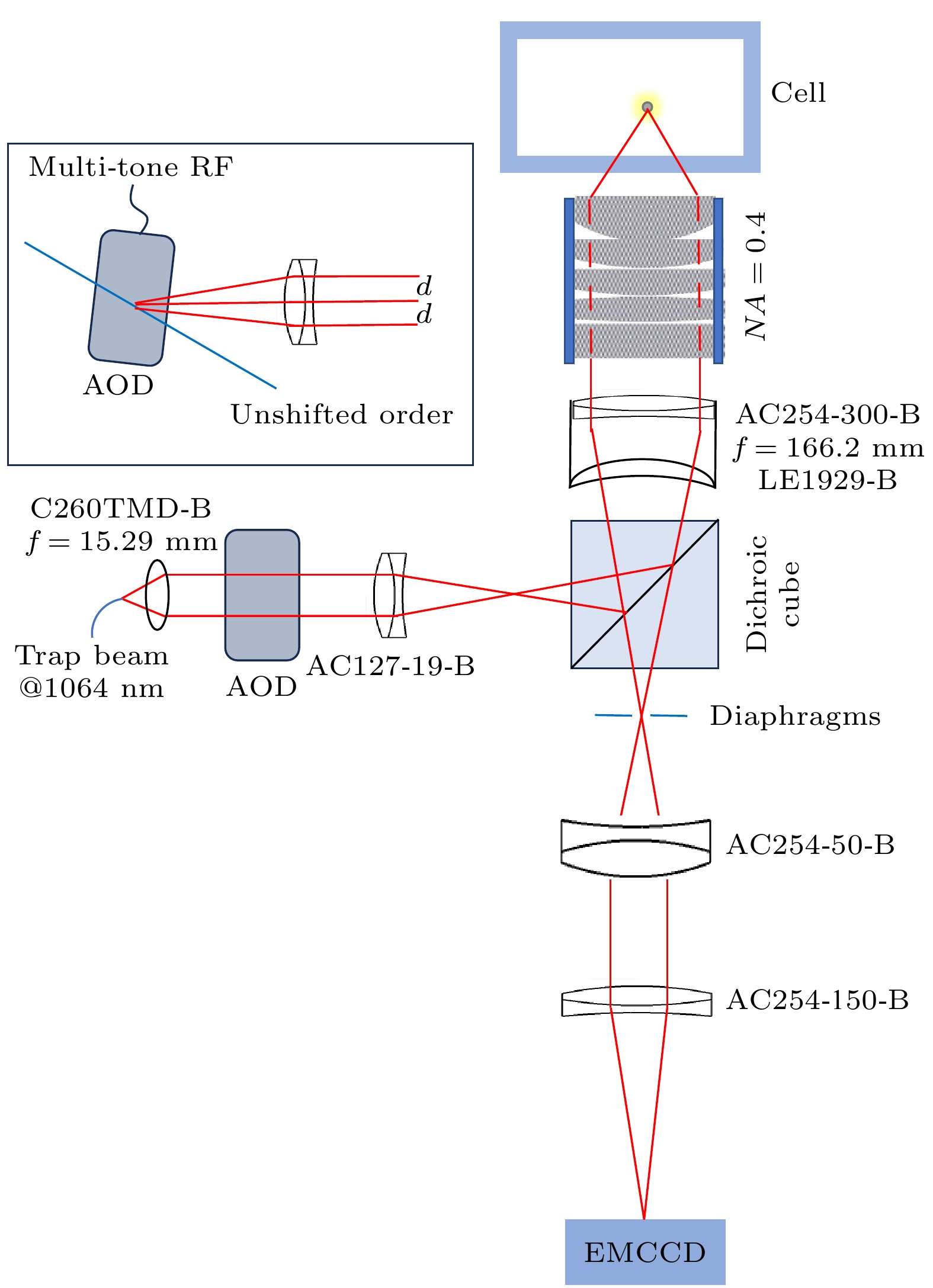
图 3 (a), (b)成像系统校准与分辨率测量, 通过成像系统分别对780 nm单模保偏光纤端面成像(a)及测试靶成像(b); (c)图(b)中第8组刻线的第3个条纹放大图; (d)图(a)灰度值强度分布; (e), (f)分别对应于水平刻线和竖直刻线强度分布图
Figure 3. Calibration and resolution measurement of the imaging system: (a), (b) Single-mode polarization-maintaining fiber end-face is imaged by the imaging system, and a test target is imaged as well; (c) zooms in on the third stripe of the eighth group of patterns in Fig. (b); (d) the intensity distribution of the grayscale values in Fig. (a); (e), (f) correspond to intensity distribution maps of horizontal and vertical stripes, respectively.
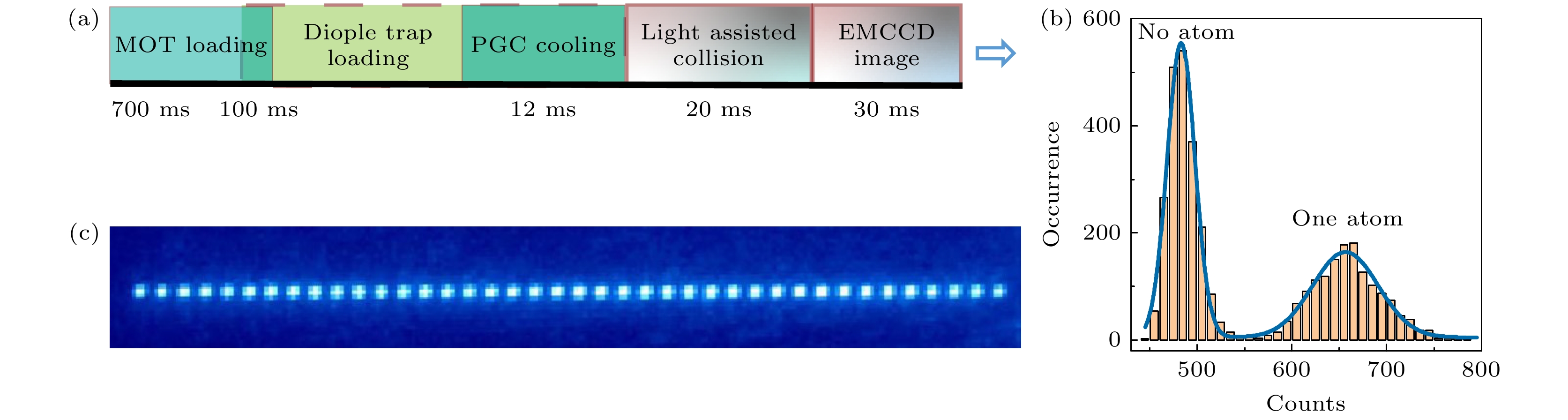
图 4 实验过程与单原子阵列荧光成像 (a)实验时序图; (b)单原子信号统计直方图(图(c)中从左往右第13个偶极阱), 曝光时间为30 ms, 测量次数为3600, 浅蓝色线为双峰高斯函数拟合曲线; (c)单原子阵列荧光信号叠加图, 叠加次数为500
Figure 4. Experimental process and fluorescence imaging of a single-atom array: (a) Experimental timing sequence; (b) histogram of single-atom signals (the 13th dipole trap from left to right in Fig. (c)), with an exposure time of 30 ms and a total measurement times of 3600, the light blue line represents the fitted curve using a bimodal Gaussian function; (c) fluorescence signal superimposed image of single-atom array, with a total of 500 superimpositions.
图 5 单原子阵列光频移和振荡频率均匀性 (a)不同偶极阱引起原子光频移分布图, 插图实验结果可用于确定偶极阱 13 中原子的光频移; (b)不同偶极阱内原子振荡频率分布图, 插图为偶极阱 13 通过释放再俘获方法测量得到的实验结果, 用于确定原子的振荡频率. 图中的误差棒为拟合误差
Figure 5. Uniformity of light shift and oscillation frequency in single-atom array: (a) Distribution of light shift caused by different dipole trap, with inset showing the experimental results that can be used to determine the light frequency shift of atoms in dipole trap 13; (b) distribution of oscillation frequencies within different dipole traps, with inset indicating the experimental results obtained through the release-recapture method for measuring dipole trap 13, which can be used to determine the oscillation frequency of atoms. The error bars in panels (a) and (b) represent fitting errors.
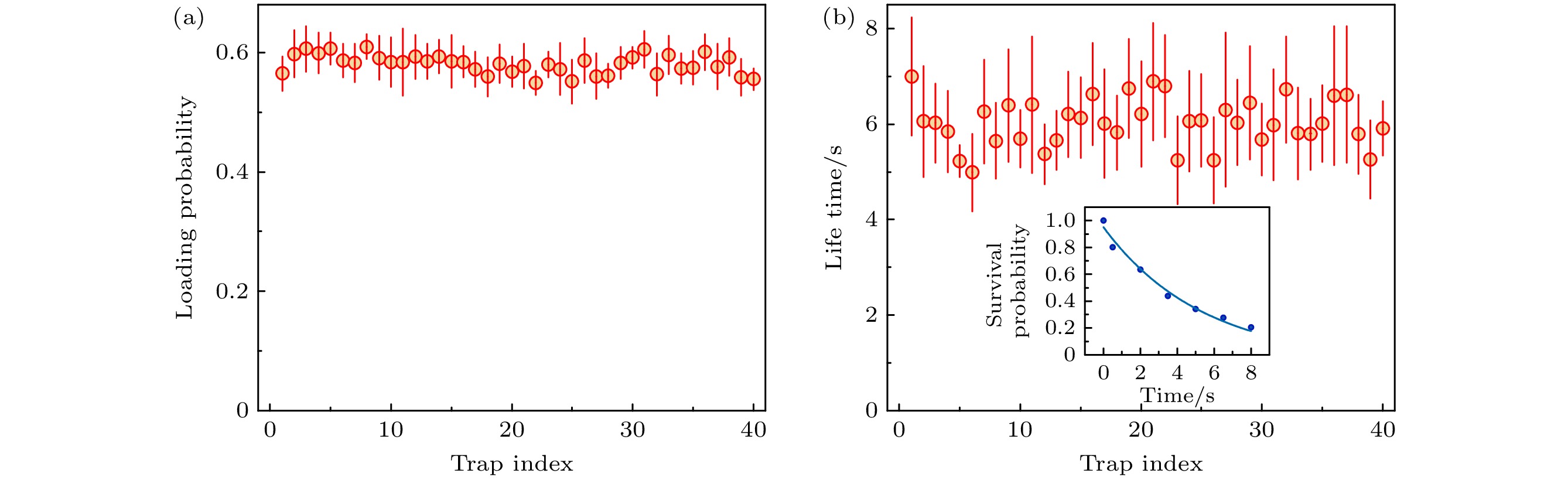
图 6 单原子阵列装载率和寿命均匀性 (a)不同偶极阱单原子装载概率分布图, 误差棒为多次测量结果的标准差; (b)不同偶极阱内单原子暗阱寿命分布图, 误差棒为拟合误差, 插图为偶极阱13暗阱寿命测量结果
Figure 6. Uniformity of loading probability and lifetime in the single-atom array: (a) Distribution of loading probability in different dipole trap, the error bar is the standard deviation of multiple measurement results; (b) distribution of lifetime in different dipole trap, the error bars represent fitting errors, the inset presents the measurement results of the dark trap lifetime in dipole trap 13.
-
[1] Weiss D S, Saffman M 2017 Phys. Today 70 44
Google Scholar
[2] Bruzewicz C D, McConnell R, Chiaverini J, Sage J M 2016 Nat. Commun. 7 13005
Google Scholar
[3] Gong M, Chen M C, Zheng Y R, Wang S Y, Zha C, Deng H, Yan Z G, Rong H, Wu Y L, Li S W, Chen F S, Zhao Y W, Liang F T, Lin J, Xu Y, Guo C, Sun L H, Castellano A D, Wang H H, Peng C Z, Lu C Y, Zhu X B, Pan J W 2019 Phys. Rev. Lett. 122 110501
Google Scholar
[4] Singh K, Anand S, Pocklington A, Kemp J T, Bernien H 2022 Phy. Rev. X 12 011040
[5] Bernien H, Schwartz S, Keesling A, Levine H, Omran A, Pichler H, Choi S, Zibrov A S, Endres M, Vuletić V, Lukin M D 2017 Nature 551 579
Google Scholar
[6] Labuhn H, Barredo D, Ravets S, Léséleuc S D, Macrì T, Lahaye T, Browaeys A 2016 Nature 534 667
Google Scholar
[7] Ebadi S, Wang T T, Levine H, Keesling A, Semeghini G, Omran A, Bluvstein D, Samajdar R, Pichler H, Ho W W, Choi S, Sachdev S, Greiner M, Vladan Vuletić V, Lukin M D 2021 Nature 595 227
Google Scholar
[8] Scholl P, Schuler M, Williams H J, Eberharter A A, Barredo D, Schymik K N, Lienhard V, Henry L P, Lang T C, Lahaye T, Läuchli A M, Browaeys A 2021 Nature 595 233
Google Scholar
[9] Norcia M A, Cairncross W B, Barnes K, et al. 2023 Phys. Rew. X 13 041034
[10] Singh K, Bradley C E, Anand S, Ramesh V, White R, Bernien H 2023 Science 380 126
Google Scholar
[11] Evered S J, Bluvstein D, Kalinowski M, Ebadi S, Manovitz T, Zhou H, Li S H, Geim A A, Wang T T, Maskara N, Levine H, Semeghini G, Greiner M, Vuletic V, Lukin M D 2023 Nature 622 268
Google Scholar
[12] Graham T M, Song Y, Scott J, Poole C, Phuttitarn L, Jooya K, Eichler P, Jiang X, Marra A, Grinkemeyer B, Kwon M, Ebert M, Cherek J, Lichtman M T, Gillette M, Gilbert J, Bowman D, Ballance T, Campbell C, Dahl E D, Crawford O, Blunt N S, Rogers B, Noel T, Saffman M 2023 Nature 604 457
Google Scholar
[13] Bluvstein D, Evered S J, Geim A A, Li S H, Zhou H, Manovitz T, Ebadi S, Cain M, Kalinowski M, Hangleiter D, Ataides J P B, Maskara N, Cong I, Gao X, Rodriguez P S, Karolyshyn T, Semeghini G, Gullans M J, Greiner M, Vuletic V, Lukin M D 2024 Nature 626 58
Google Scholar
[14] Barredo D, De Léséleuc S, Lienhard V, Lahaye T, Browaeys A 2016 Science 354 1021
Google Scholar
[15] Endres M, Bernien H, Keesling A, Levine H, Anschuetz E R, Krajenbrink A, Lukin M D 2016 Science 354 1024
Google Scholar
[16] Brown M O, Thiele T, Kiehl C, Hsu T W, Regal C A 2019 Phys. Rev. X 9 011057
[17] Semeghini G, Levine H, Keesling A, Ebadi S, Wang T T, Bluvstein D, Verresen R, Pichler H, Kalinowski M, Lukin M D 2021 Science 374 1242
Google Scholar
[18] Sergi J F, Joseph V, Alexandre D 2024 arXiv: 2402.02852 [cond-mat.quant-gas]
[19] Liu Y X, Wang Z H, Yang P F, Wang Q X, Fan Q, Guan S J, Li G, Zhang P F, Zhang T C 2023 Phys. Rev. Lett. 130 173601
Google Scholar
[20] Deist E, Gerber J A, Lu Y H, Zeiher J, Stamper-Kurn D M 2022 Phys. Rev. Lett. 128 083201
Google Scholar
[21] Ðorđević T, Samutpraphoot P, Ocola P L, Bernien H, Grinkemeyer B, Dimitrova I, Vuletić V, Lukin M D 2021 Science 373 1511
Google Scholar
[22] Deist E, Lu Y H, Ho J, Pasha M K, Zeiher J, Yan Z, Stamper-Kurn D M 2022 Phys. Rev. Lett. 129 203602
Google Scholar
[23] Yan Z J, Jacquelyn H, Lu Y H, Masson S J, Asenjo-Garcia A, Stamper-Kurn D M 2023 Phys. Rev. Lett. 131 253603
Google Scholar
[24] Li S K, Li G, Wu W, Fan Q, TianY L, Yang P F, Zhang P F, Zhang T C 2020 Rev. Sci. Instrum. 91 043104
Google Scholar
[25] Schlosser N, Reymond G, Grangier P 2002 Phys. Rev. Lett. 89 023005
Google Scholar
[26] Sortais Y R P, Marion H, Tuchendler C, Lance A M, Lamare M, Fournet P, Armellin C, Mercier R, Messin G, Browaeys A, Grangier P 2007 Phys. Rev. A 75 013406
Google Scholar
[27] Sheng C, He X, Xu P, Guo R, Wang K, Xiong Z, Liu M, Wang J, Zhan M 2018 Phys. Rev. Lett. 121 240501
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1948
- PDF Downloads: 106
- Cited By: 0
