-
Magnetic skyrmion is a kind of nontrivial topological magnetic structure, which can exist stably in chiral magnet with Dzyaloshinskii-Moriya (DM) interaction, and its static and dynamic properties are closely related to its structural characteristics. However, there are no general analytical expressions for skyrmion profiles. Therefore, many researchers have provided approximate solutions. In this paper, a new approach to exploring magnetic skyrmion structures is introduced by using a symbolic regression approach. Considering the influence of DM interaction and external magnetic field on magnetic skyrmion structure, two suitable approximate expressions are obtained through symbolic regression algorithms. The applicability of these expressions depends on the dominant interaction. The research results in this work validate the powerful capability of symbolic regression algorithms in exploring the magnetic skyrmion profiles. So, the present study provides a new method for finding the analytical expressions for magnetic structure.
-
Keywords:
- magnetic skyrmions /
- symbolic regression /
- structures of magnetic skyrmions /
- Dzyaloshinskii-Moriya interaction
[1] Abanov Ar, Pokrovsky V L 1998 Phys. Rev. B 58 R8889
Google Scholar
[2] Rößler U K, Bogdanov A N, Pfleiderer C 2006 Nature 442 797
Google Scholar
[3] Heinze S, von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R, Bihlmayer G, Bluegel S 2011 Nat. Phys. 7 713
Google Scholar
[4] Wei W S, He Z D, Qu Z, Du H F 2021 Rare Met. 40 3076
Google Scholar
[5] Ye C, Li L L, Shu Y, Li Q R, Xia J, Hou Z P, Zhou Y, Liu X X, Yang Y Y, Zhao G P 2022 Rare Met. 41 2200
Google Scholar
[6] Braun H 1994 Phys. Rev. B 50 16485
Google Scholar
[7] Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R 2015 Phys. Rev. Lett. 114 177203
Google Scholar
[8] Rohart S, Thiaville A 2013 Phys. Rev. B 88 184422
Google Scholar
[9] Zhou Y, Iacocca E, Awad A A, Dumas R K, Zhang F C, Braun H B, Akerman J 2015 Nat. Commun. 6 8193
Google Scholar
[10] Buttner F, Lemesh I, Beach G S D 2018 Sci. Rep. 8 4464
Google Scholar
[11] Komineas S, Melcher C, Venakides S 2020 Nonlinearity 33 3395
Google Scholar
[12] Komineas S, Melcher C, Venakides S 2021 Physica D 418 132842
Google Scholar
[13] Komineas S, Melcher C, Venakides S 2023 New J. Phys. 25 023013
Google Scholar
[14] Udrescu S M, Tegmark M 2020 Sci. Adv. 6 eaay2631
Google Scholar
[15] Kim S, Lu P Y, Mukherjee S, Gilbert M, Jing L, Ceperic V, Soljacic M 2021 IEEE Trans. Neural Networks Learn. Syst. 32 4166
Google Scholar
[16] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[17] Sun S, Ouyang R, Zhang B, Zhang T Y 2019 MRS Bull. 44 559
Google Scholar
[18] Koksbang S M 2023 Phys. Rev. D 107 103522
Google Scholar
[19] Hernandez A, Balasubramanian A, Yuan F, Mason S A M, Mueller T 2019 NPJ Comput. Mater. 5 112
Google Scholar
[20] Baldi P, Sadowski P, Whiteson D 2014 Nat. Commun. 5 4308
Google Scholar
[21] Carleo G, Troyer M 2017 Science 355 602
Google Scholar
[22] Zhao G P, Zhao L, Shen L C, Zou J, Qiu L 2019 Chin. Phys. B 28 77505
Google Scholar
[23] Jones A 1993 Nature 363 222
Google Scholar
[24] Cranmer M 2023 arXiv: 10.48550/arXiv.2305.01582 [astro-ph.IM
[25] Wu H, Hu X, Jing K, Wang X R 2021 Commun. Phys. UK 4 1
Google Scholar
-
图 1 磁性斯格明子结构 (a) 布洛赫型斯格明子; (b) 奈尔型斯格明子; (c)单磁畴壁
Figure 1. Magnetic skyrmion structures: (a) Bloch-type skyrmion; (b) Néel-type skyrmion; (c) magnetic domain wall.
图 2 符号回归算法中二叉树结构与遗传操作示意图 (a) 用二叉树表示公式形式; (b) 复制操作; (c) 交叉操作; (d) 变异操作
Figure 2. Binary tree structure and schematic diagrams of genetic operations in symbolic regression: (a) Representing the formula in binary tree form; (b) copy operation; (c) crossover operation; (d) mutation operation.
图 3 符号回归方法流程图
Figure 3. Flowchart of the symbolic regression.
图 4 不同A与K值下, (8)式拟合结果与一维单磁畴壁结构模拟数据比较图 (a) A = 1×10–12 J/m, K = 1×103 J/m3; (b) A = 5×10–12 J/m, K = 2×103 J/m3; (c) A = 13×10–12 J/m, K = 3×103 J/m3
Figure 4. Comparison between the fitting results of Eq. (8) and simulation data of one-dimensional magnetic domain wall under various values of A and K: (a) A = 1×10–12 J/m, K = 1×103 J/m3; (b) A = 5×10–12 J/m, K = 2×103 J/m3; (c) A = 13×10–12 J/m, K = 3×103 J/m3.
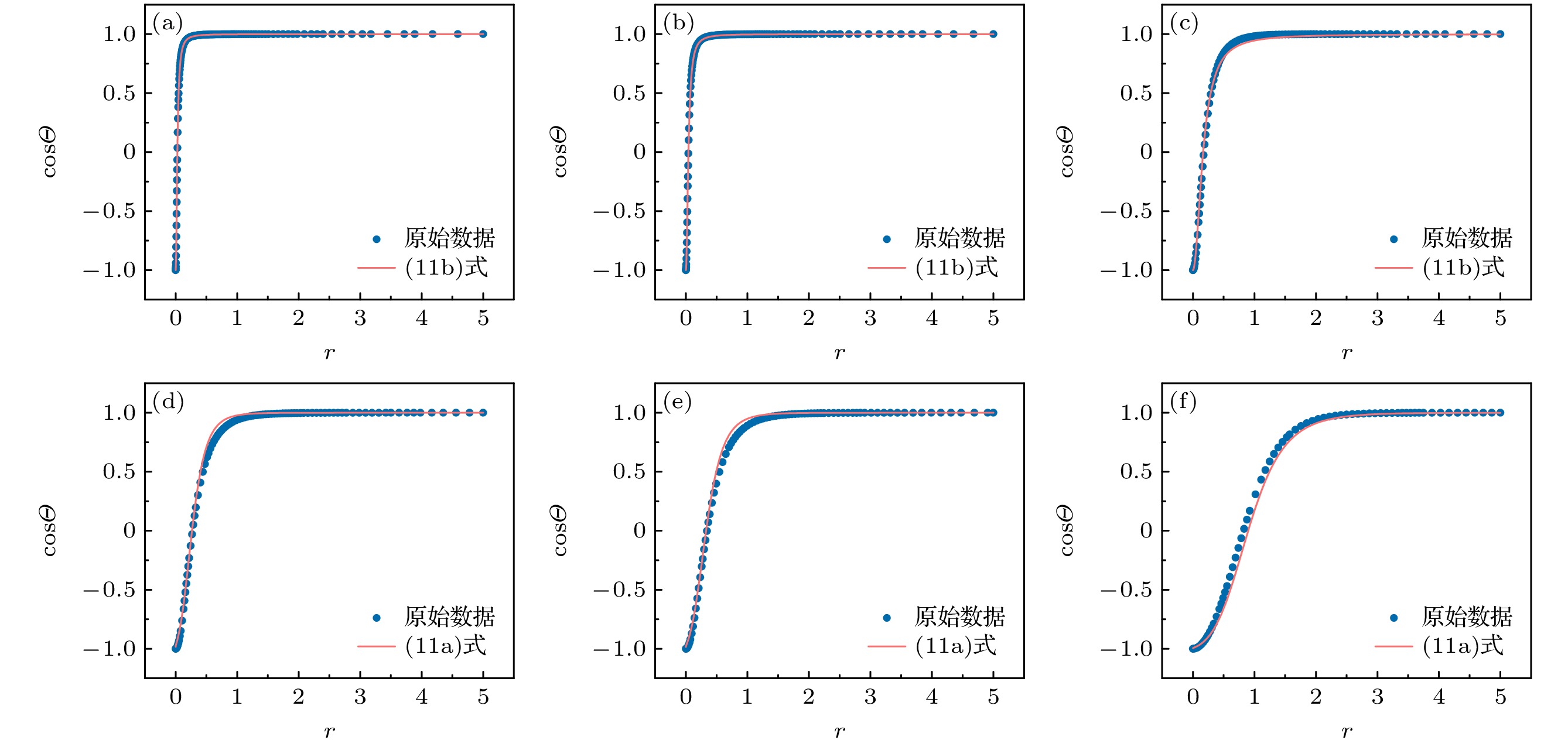
图 6 不同$ {\lambda }^{2}/h $大小下(10a)式与 (10b)式的拟合情况 (a) 0.01; (b) 0.16; (c) 0.167; (d) 0.9. (e) 不同$ {\lambda }^{2}/h $大小下, 更高适应度解析式统计图(1代表(10a)式, 2代表(10b)式)
Figure 6. Fitting results of equations (10a) and (10b) under various $ {\lambda }^{2}/h $ values: (a) 0.01; (b) 0.16; (c) 0.167; (d) 0.9$ . $ (e) Statistical chart of equations with higher fitness under various $ {\lambda }^{2}/h $ values (1 represents equation (10a), 2 represents equation (10b)).
-
[1] Abanov Ar, Pokrovsky V L 1998 Phys. Rev. B 58 R8889
Google Scholar
[2] Rößler U K, Bogdanov A N, Pfleiderer C 2006 Nature 442 797
Google Scholar
[3] Heinze S, von Bergmann K, Menzel M, Brede J, Kubetzka A, Wiesendanger R, Bihlmayer G, Bluegel S 2011 Nat. Phys. 7 713
Google Scholar
[4] Wei W S, He Z D, Qu Z, Du H F 2021 Rare Met. 40 3076
Google Scholar
[5] Ye C, Li L L, Shu Y, Li Q R, Xia J, Hou Z P, Zhou Y, Liu X X, Yang Y Y, Zhao G P 2022 Rare Met. 41 2200
Google Scholar
[6] Braun H 1994 Phys. Rev. B 50 16485
Google Scholar
[7] Romming N, Kubetzka A, Hanneken C, von Bergmann K, Wiesendanger R 2015 Phys. Rev. Lett. 114 177203
Google Scholar
[8] Rohart S, Thiaville A 2013 Phys. Rev. B 88 184422
Google Scholar
[9] Zhou Y, Iacocca E, Awad A A, Dumas R K, Zhang F C, Braun H B, Akerman J 2015 Nat. Commun. 6 8193
Google Scholar
[10] Buttner F, Lemesh I, Beach G S D 2018 Sci. Rep. 8 4464
Google Scholar
[11] Komineas S, Melcher C, Venakides S 2020 Nonlinearity 33 3395
Google Scholar
[12] Komineas S, Melcher C, Venakides S 2021 Physica D 418 132842
Google Scholar
[13] Komineas S, Melcher C, Venakides S 2023 New J. Phys. 25 023013
Google Scholar
[14] Udrescu S M, Tegmark M 2020 Sci. Adv. 6 eaay2631
Google Scholar
[15] Kim S, Lu P Y, Mukherjee S, Gilbert M, Jing L, Ceperic V, Soljacic M 2021 IEEE Trans. Neural Networks Learn. Syst. 32 4166
Google Scholar
[16] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[17] Sun S, Ouyang R, Zhang B, Zhang T Y 2019 MRS Bull. 44 559
Google Scholar
[18] Koksbang S M 2023 Phys. Rev. D 107 103522
Google Scholar
[19] Hernandez A, Balasubramanian A, Yuan F, Mason S A M, Mueller T 2019 NPJ Comput. Mater. 5 112
Google Scholar
[20] Baldi P, Sadowski P, Whiteson D 2014 Nat. Commun. 5 4308
Google Scholar
[21] Carleo G, Troyer M 2017 Science 355 602
Google Scholar
[22] Zhao G P, Zhao L, Shen L C, Zou J, Qiu L 2019 Chin. Phys. B 28 77505
Google Scholar
[23] Jones A 1993 Nature 363 222
Google Scholar
[24] Cranmer M 2023 arXiv: 10.48550/arXiv.2305.01582 [astro-ph.IM
[25] Wu H, Hu X, Jing K, Wang X R 2021 Commun. Phys. UK 4 1
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3121
- PDF Downloads: 135
- Cited By: 0
