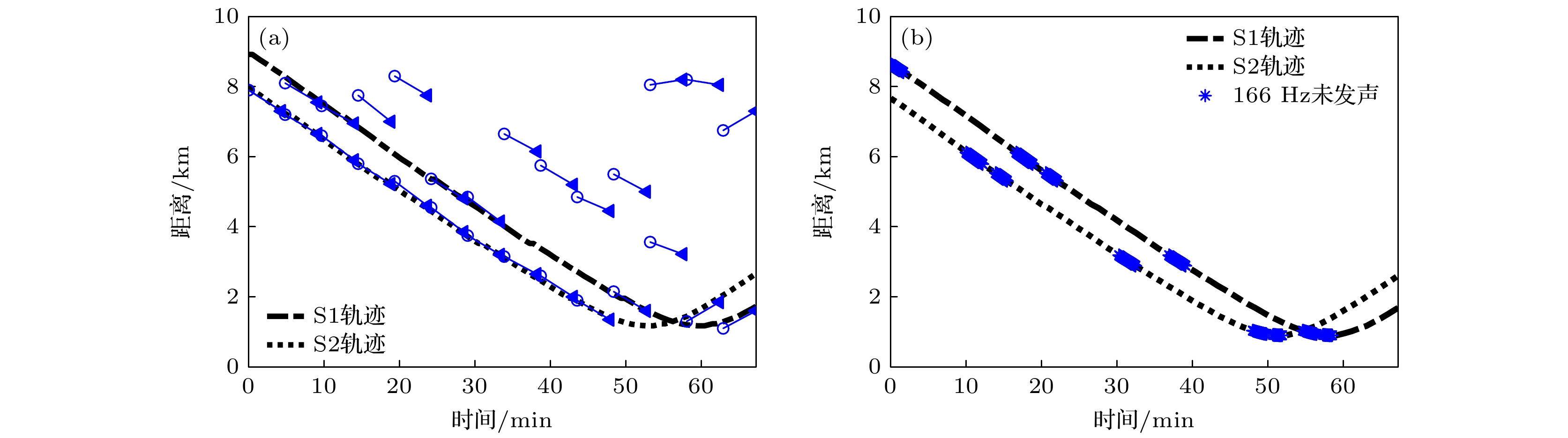
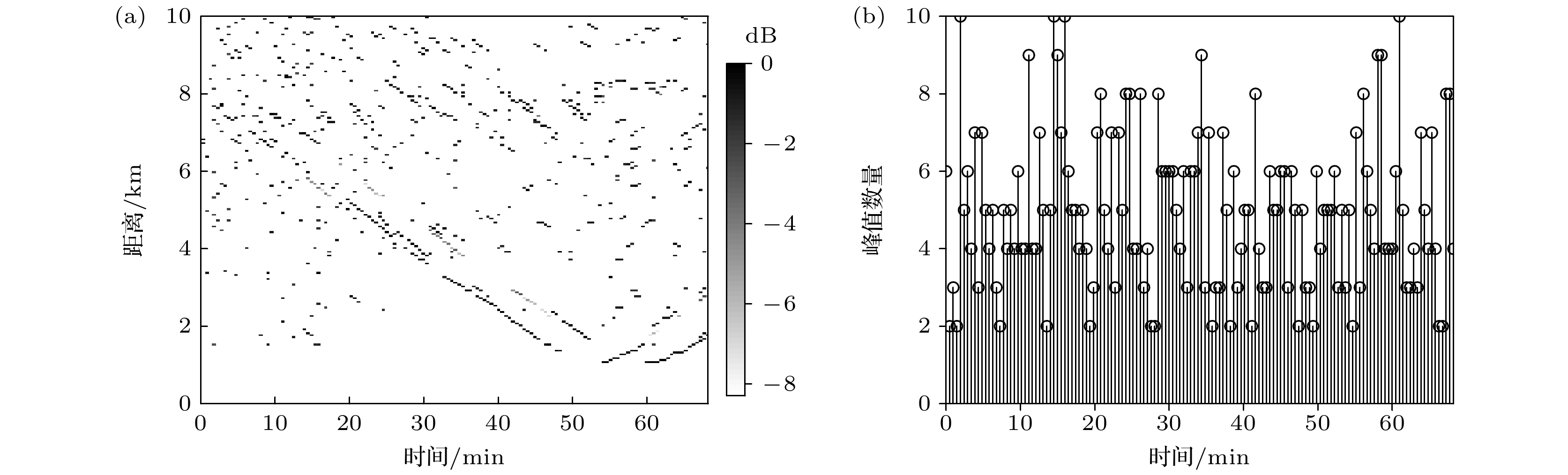
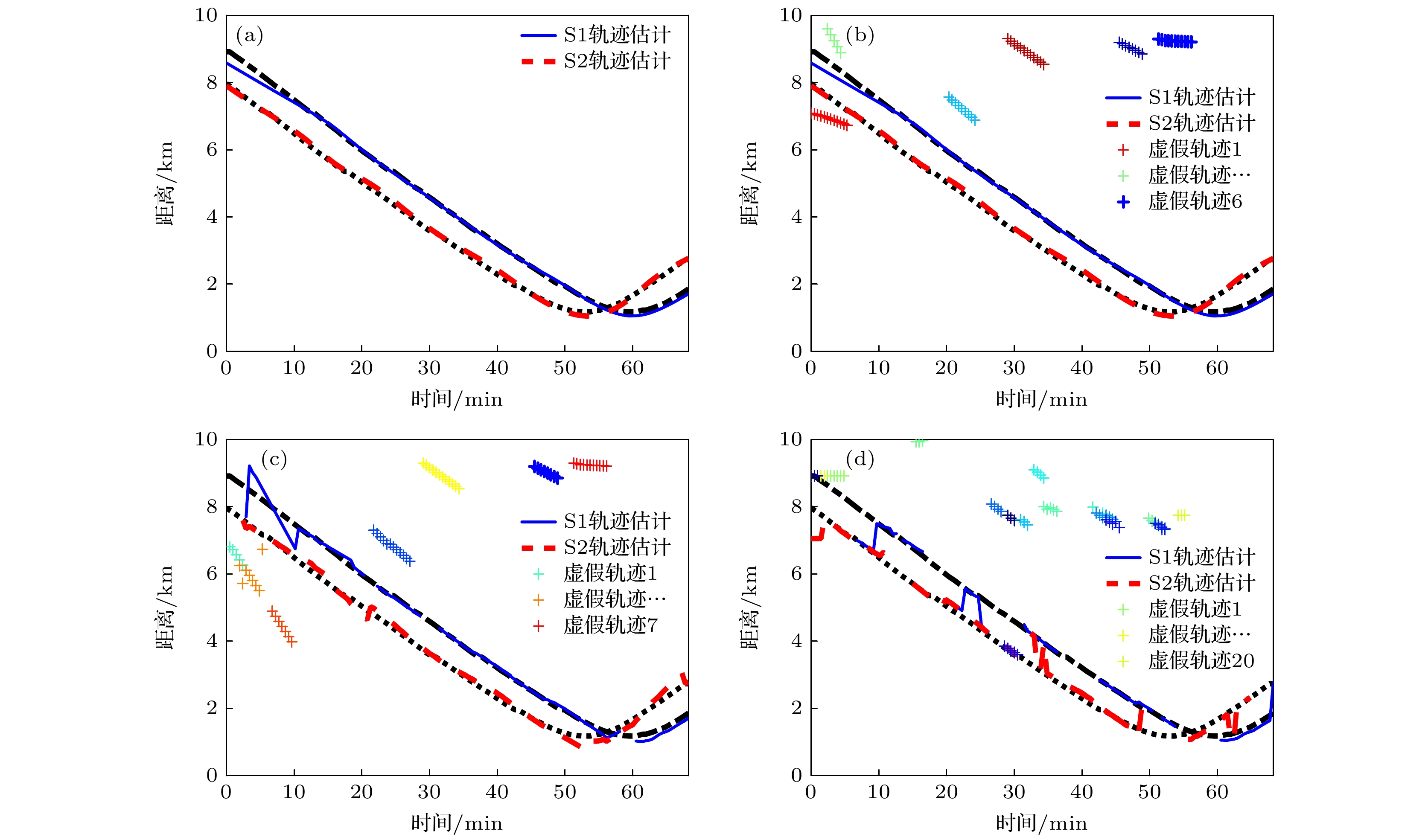
-
In the shallow water waveguide, matched field tracking methods use the continuity of the peak position of the moving source and the disorder of pseudo-peaks on the sequential ambiguity surfaces to track the underwater source trajectory. However, owing to the dual influence of the space-time fluctuating shallow water waveguide environment and the complex sources motion scene, the existing matching field tracking methods are prone to track interruption, switches and false track phenomena, leading to discontinuous tracking results. Using the consistency between the peak position distance likelihood and the peak amplitude likelihood of sequential ambiguity surfaces, a continuous matched field tracking method is proposed based on the trajectory Poisson multi-Bernoulli mixture filter in this paper. The proposed method is applied to SWellEx-96 experimental data, and the tracking performance is measured by the linear programming metric. The results show that compared with the existing matching field tracking method and multi-target tracking method via random finite set, the proposed method achieves continuous tracking and accurate quantity estimation of moving sources trajectory. Among them, the prediction step and updating step in the trajectory space can avoid the phenomenon of trajectory interruption and switches in unvoiced periods.
-
Keywords:
- shallow water waveguide /
- matched field tracking /
- a scene of intermittent vocalization /
- continuous trajectory
[1] Bucker H 1976 J. Acoust. Soc. Am. 59 368
Google Scholar
[2] Bucker H 1994 J. Acoust. Soc. Am. 96 3809
Google Scholar
[3] Fialkowski L T, Perkins J S, Collins M D 2001 J. Acoust. Soc. Am. 110 739
Google Scholar
[4] Maranda B H, Fawcett J A 1991 IEEE J. Ocean. Eng. 16 189
Google Scholar
[5] Fawcett J A, Maranda B H 1993 J. Acoust. Soc. Am. 94 1363
Google Scholar
[6] Zala C A, Ozard J M, Wilmut M J 1998 J. Acoust. Soc. Am. 103 374
Google Scholar
[7] Tantum S L, Nolte L W 2002 J. Acoust. Soc. Am. 112 119
Google Scholar
[8] Mahler R P 2014 Advances in Statistical Multisource-Multitarget Information Fusion (Boston, London: Artech house) p83
[9] Yardim C, Michalopoulou Z, Gerstoft P 2011 IEEE J. Ocean. Eng. 36 71
Google Scholar
[10] Vo B N, Ma W K 2006 IEEE Trans. Signal. Proces. 54 4091
Google Scholar
[11] Gruden P, White P R 2016 J. Acoust. Soc. Am. 140 1981
Google Scholar
[12] Gruden P, White P R 2016 J. Acoust. Soc. Am. 148 3014
Google Scholar
[13] Gruden P, Nosal E M 2021 J. Acoust. Soc. Am. 150 3399
Google Scholar
[14] Kupilik M J, Petersen T 2014 J. Acoust. Soc. Am. 136 1736
Google Scholar
[15] Georgescu R, Willett P 2012 IEEE J. Ocean. Eng. 37 220
Google Scholar
[16] García-Fernández Á F, Williams J L 2018 IEEE Trans. Signal. Proces. 54 1883
Google Scholar
[17] García-Fernández Á F, Svensson L 2020 IEEE Trans. Signal. Proces. 68 4933
Google Scholar
[18] Vo B T, Vo B N 2013 IEEE Trans. Signal. Proces. 61 3460
Google Scholar
[19] Tracey B H 2005 J. Acoust. Soc. Am. 118 1372
Google Scholar
[20] Lerro D, Bar-Shalom Y 1993 IEEE Trans. Aerosp. Electron. Syst. 29 404
Google Scholar
[21] Bendat J S, Piersol A G 2010 Random Data: Analysis and Measurement Procedures (4th Ed.) (Hoboken, NJ: Wiley) p604
[22] Murray J, Ensberg D The SWellEx-96 experiment http://swellex96.ucsd.edu/ (Last viewed July 2021
[23] Porter M B 1991 The KRAKEN Normal Mode Program (La Spezia: SACLANT Undersea Research Centre
[24] Gemba K L, Nannuru S 2017 J. Acoust. Soc. Am. 141 3411
Google Scholar
[25] Booth N O, Baxley P A 1996 IEEE J. Ocean. Eng. 21 402
Google Scholar
[26] García-Fernández Á F, Rahmathullah A S 2020 IEEE Trans. Signal. Proces. 68 3917
Google Scholar
-
图 1 SWellEx-96测线S5实验 (a)发射船轨迹; (b)波导环境示意图
Figure 1. The SWellEx-96 event S5: (a) The launch ship track; (b) SWellEx-96 waveguide.
图 2 双目标距离维轨迹 (a) 现有匹配场跟踪方法轨迹估计结果; (b) 轨迹真值
Figure 2. Range dimension trajectory of two targets: (a) MFT result; (b) the truth.
图 3 匹配场跟踪性能影响因素 (a)沿轨迹的水深变化; (b)平均阵元接收信噪比; (c)相关系数
Figure 3. Influencing factors of matching field tracking performance: (a) The bottom depth along the trajectory; (b) average element level SNR; (c) correlation coefficient.
图 4 所有时间步测量集合 (a) 距离维空间分布; (b) 元素数量
Figure 4. Measurements sets of all steps: (a) Spatial distribution of measurement elements in range dimension; (b) the number of elements in the measurement set.
图 5 四种方法的距离维轨迹估计结果 (a) TPMBM-A-MFT; (b) TPMBM-MFT; (c) PMBM-MFT; (d) GMPHD-MFT
Figure 5. Range dimension trajectory estimation results for four methods: (a) TPMBM-A-MFT; (b) TPMBM-MFT; (c) PMBM-MFT; (d) GMPHD-MFT.
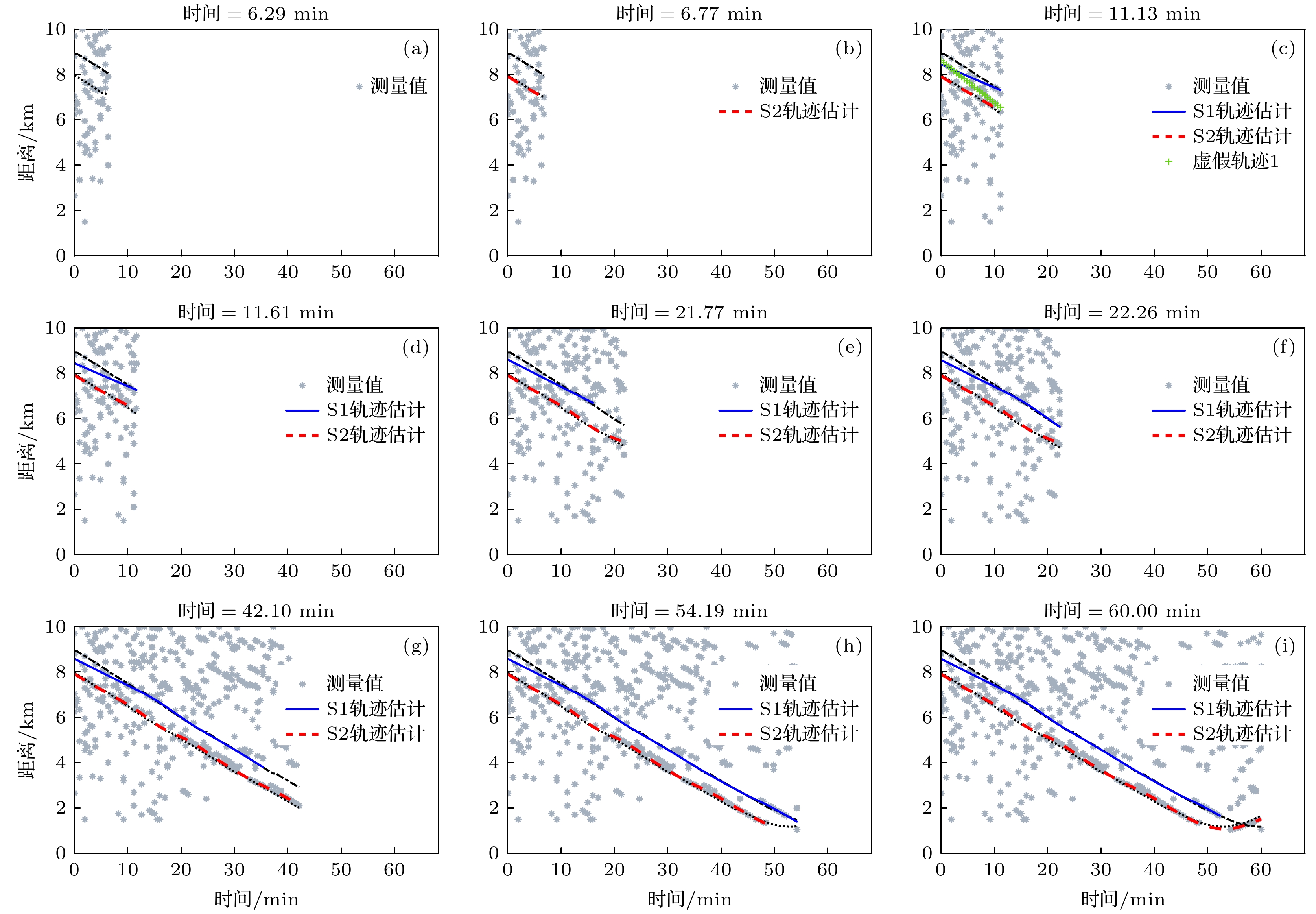
图 6 TPMBM-A-MFT的跟踪过程 (a)第6.29 min; (b)第6.77 min; (c)第11.13 min; (d)第11.61 min; (e)第21.77 min; (f)第22.26 min; (g)第42.10 min; (h)第54.19 min; (i)第60.00 min
Figure 6. Tracking process of TPMBM-A-MFT method: (a) 6.29 minutes; (b) 6.77 minutes; (c) 11.13 minutes; (d) 11.61 minutes; (e) 21.77 minutes; (f) 22.26 minutes; (g) 42.10 minutes; (h) 54.19 minutes; (i) 60.00 minutes.
图 7 四种跟踪方法在每个时间步的LP度量结果
Figure 7. LP metrics at each time step for four methods.
图 8 LP的4种分解度量 (a)匹配位置误差; (b)轨迹缺失代价; (c)虚假轨迹代价; (d)轨迹混叠代价
Figure 8. Four decomposition metrics of LP: (a) Matched localization error; (b) missed trajectory cost; (c) false trajectory cost; (d) switching cost.
表 1 TPMBM-A-MFT算法流程
Table 1. Steps of TPMBM-A-MFT algorithm.
步骤1 建立匹配场轨迹状态空间模型
变换模糊度函数: (26)式;
给出状态方程和观测方程: (27)式和(28)式;步骤2 根据(27)式对$ p({{\bf X}_k}) $参数集预测: 2.2.1节; 步骤3 根据(28)式对$ p({{\bf X}_k}) $参数集更新: 2.2.2节; 步骤4 结合峰值位置与幅度实现数据关联: (36)式; 步骤5 估计轨迹状态和数量: (25)式. 注: 初始时间步中$ {\bf{X} }_{k = 1}^{\rm{d}} = \varnothing $且泊松强度$ \lambda _{k = 1}^{\rm{u}} = \lambda _{k = 1}^{\rm{b}} $. 
DownLoad: CSV
表 2 匹配场跟踪过程的滤波参数设置
Table 2. Filter parameters setup for matched field tracking process.
${q_r}$ ${q_d}$ ${\sigma _r}$ ${\sigma _d}$ $T$ ${w^{\text{b}}}$ ${P^{\text{S}}}$ ${P^{\text{D}}}$ $\varGamma $ $6 \times {10^{ - 3}}$ $6 \times {10^{ - 3}}$ $0.05$ $2$ $1$ $5 \times {10^{ - 3}}$ $0.99$ $\{ 0.2, 0.5\} $ $0.1$
DownLoad: CSV
-
[1] Bucker H 1976 J. Acoust. Soc. Am. 59 368
Google Scholar
[2] Bucker H 1994 J. Acoust. Soc. Am. 96 3809
Google Scholar
[3] Fialkowski L T, Perkins J S, Collins M D 2001 J. Acoust. Soc. Am. 110 739
Google Scholar
[4] Maranda B H, Fawcett J A 1991 IEEE J. Ocean. Eng. 16 189
Google Scholar
[5] Fawcett J A, Maranda B H 1993 J. Acoust. Soc. Am. 94 1363
Google Scholar
[6] Zala C A, Ozard J M, Wilmut M J 1998 J. Acoust. Soc. Am. 103 374
Google Scholar
[7] Tantum S L, Nolte L W 2002 J. Acoust. Soc. Am. 112 119
Google Scholar
[8] Mahler R P 2014 Advances in Statistical Multisource-Multitarget Information Fusion (Boston, London: Artech house) p83
[9] Yardim C, Michalopoulou Z, Gerstoft P 2011 IEEE J. Ocean. Eng. 36 71
Google Scholar
[10] Vo B N, Ma W K 2006 IEEE Trans. Signal. Proces. 54 4091
Google Scholar
[11] Gruden P, White P R 2016 J. Acoust. Soc. Am. 140 1981
Google Scholar
[12] Gruden P, White P R 2016 J. Acoust. Soc. Am. 148 3014
Google Scholar
[13] Gruden P, Nosal E M 2021 J. Acoust. Soc. Am. 150 3399
Google Scholar
[14] Kupilik M J, Petersen T 2014 J. Acoust. Soc. Am. 136 1736
Google Scholar
[15] Georgescu R, Willett P 2012 IEEE J. Ocean. Eng. 37 220
Google Scholar
[16] García-Fernández Á F, Williams J L 2018 IEEE Trans. Signal. Proces. 54 1883
Google Scholar
[17] García-Fernández Á F, Svensson L 2020 IEEE Trans. Signal. Proces. 68 4933
Google Scholar
[18] Vo B T, Vo B N 2013 IEEE Trans. Signal. Proces. 61 3460
Google Scholar
[19] Tracey B H 2005 J. Acoust. Soc. Am. 118 1372
Google Scholar
[20] Lerro D, Bar-Shalom Y 1993 IEEE Trans. Aerosp. Electron. Syst. 29 404
Google Scholar
[21] Bendat J S, Piersol A G 2010 Random Data: Analysis and Measurement Procedures (4th Ed.) (Hoboken, NJ: Wiley) p604
[22] Murray J, Ensberg D The SWellEx-96 experiment http://swellex96.ucsd.edu/ (Last viewed July 2021
[23] Porter M B 1991 The KRAKEN Normal Mode Program (La Spezia: SACLANT Undersea Research Centre
[24] Gemba K L, Nannuru S 2017 J. Acoust. Soc. Am. 141 3411
Google Scholar
[25] Booth N O, Baxley P A 1996 IEEE J. Ocean. Eng. 21 402
Google Scholar
[26] García-Fernández Á F, Rahmathullah A S 2020 IEEE Trans. Signal. Proces. 68 3917
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3599
- PDF Downloads: 60
- Cited By: 0
