-
匹配场声源功率估计方法解决了传统球面波或柱面波假设下的声源功率估计方法受浅海波导效应影响较大的问题, 但浅海波导环境不确定性会严重影响匹配场声源功率估计结果的准确性. 本文定义声源功率估计性能环境失配敏感度, 量化表示环境不确定时匹配场声源功率估计性能的损失, 推导了声源功率估计性能损失与信道传递函数估计偏差的关系, 利用信道传递函数估计值与理想值的模值偏差和夹角表示. 在此基础上, 研究了环境不确定性影响声源功率估计的机理, 以及海水深度、海水声速和沉积层声速变化对声源功率估计的影响程度. 研究表明, 不同环境参数变化对信道传递函数模值的影响均比较小, 声源功率估计性能下降的主要原因是信道传递函数估计值与理想值的夹角变化较大. 海水深度变化对功率估计结果的影响最为显著, 沉积层声速变化对功率估计结果的影响很小, 除海水深度外, 在高频段范围内海水声速变化对功率估计结果的影响较大.The method of estimating matched field power solves the problem that the traditional method of estimating power under the assumption of spherical or cylindrical wave is greatly affected by the shallow water waveguide. However, the accuracy of the matched field power estimation is seriously affected by the environmental uncertainty. In this work, the environmental sensitivity in source power estimation is defined, and the loss of the source power estimation performance is quantified when the environment is uncertain. The relation between the loss of the source power estimation performance and the estimation deviation of the acoustic transfer function is derived by using the modulus deviation and the angle between the estimated acoustic transfer function and the ideal value. On this basis, we study the mechanism of the influence of environmental uncertainty on source power estimation, and the influences of water depth, sound speed of water and sound speed of sedimentary layer on the estimation of source power. The results show that the influences of different environmental parameters on the modulus are small, and the decline of the power estimation performance is mainly due to the fact that the angle varies greatly. The change of water depth has the most significant influence on the power estimation results, and the change of sound speed of sedimentary layer exerts little influence on the power estimation results. Beside the water depth, the change of sound speed of water has a greater influence on the power estimation results at high frequencies.
-
Keywords:
- environmental uncertainty /
- acoustic transfer function /
- mode shape function /
- power estimation
[1] 蒋国庆, 孙超, 刘雄厚, 蒋光禹 2020 哈尔滨工程大学学报 41 1493
Google Scholar
Jiang G Q, Sun C, Liu X H, Jiang G Y 2020 Journal of Harbin Engineering University 41 1493
Google Scholar
[2] 吴国清, 王美刚, 陈守虎, 马力 2007 声学学报 32 398
Google Scholar
Wu G Q, Wang M G, Chen S H, Ma L 2007 Acta Acustica 32 398
Google Scholar
[3] 高原, 时胜国 2010 声学技术 29 80
Google Scholar
Gao Y, Shi S G 2010 Technical Acoustics 29 80
Google Scholar
[4] 方尔正, 杨德森 2009 声学技术 28 91
Google Scholar
Fang E Z, Yang D S 2009 Technical Acoustics 28 91
Google Scholar
[5] 孙贵青, 杨德森, 张揽月 2002 声学学报 27 429
Google Scholar
Sun G Q, Yang D S, Zhang L Y 2002 Acta Acustica 27 429
Google Scholar
[6] 向龙凤, 孙超 2014 声学学报 39 570
Google Scholar
Xiang L F, Sun C 2014 Acta Acustica 39 570
Google Scholar
[7] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401
Google Scholar
[8] Bucker H P 1976 J. Acoust. Soc. Am. 59 368
Google Scholar
[9] Yang T C 1987 J. Acoust. Soc. Am. 82 1736
Google Scholar
[10] Yang T C 1990 J. Acoust. Soc. Am. 87 2072
Google Scholar
[11] 林建恒, 常道庆, 马力, 李学军, 蒋国健 2001 声学学报 26 217
Google Scholar
Lin J H, Chang D Q, Ma L, Li X J, Jiang G J 2001 Acta Acustica 26 217
Google Scholar
[12] 向龙凤, 孙超, 李明杨 2015 声学学报 40 779
Google Scholar
Xiang L F, Sun C, Li M Y 2015 Acta Acustica 40 779
Google Scholar
[13] Shang E C, Wang Y Y 1991 J. Acoust. Soc. Am. 89 2285
Google Scholar
[14] Del Balzo D R, Feuillade C, Rowe M M 1988 J. Acoust. Soc. Am. 83 2180
Google Scholar
[15] Hamson R M, Heitmeyer R M 1989 J. Acoust. Soc. Am. 86 1950
Google Scholar
[16] Feuillade C, Del Balzo D R, Rowe M M 1989 J. Acoust. Soc. Am. 85 2354
Google Scholar
[17] 赵航芳, 李建龙, 宫先仪 2011 哈尔滨工程大学学报 32 200
Google Scholar
Zhao H F, Li J L, Gong X Y 2011 Journal of Harbin Engineering University 32 200
Google Scholar
[18] 刘宗伟, 孙超, 杜金燕 2013 62 064303
Google Scholar
Liu Z W, Sun C, Du J Y 2013 Acta Phys. Sin. 62 064303
Google Scholar
[19] 李明杨, 孙超, 邵炫 2014 63 204302
Google Scholar
Li M Y, Sun C, Shao X 2014 Acta Phys. Sin. 63 204302
Google Scholar
[20] Dosso S E, Morley M G, Giles P M, Brooke G H, McCammon D F, Pecknold S, Hines P C 2007 J. Acoust. Soc. Am. 122 2560
Google Scholar
[21] 孔德智, 孙超, 李明杨, 卓颉, 刘雄厚 2019 68 174301
Google Scholar
Kong D Z, Sun C, Li M Y, Zhuo J, Liu X H 2019 Acta Phys. Sin. 68 174301
Google Scholar
[22] 贾雨晴, 苏林, 郭圣明, 马力 2018 67 174302
Google Scholar
Jia Y Q, Su L, Guo S M, Ma L 2018 Acta Phys. Sin. 67 174302
Google Scholar
[23] Porter M B, Tolstoy A 1994 J. Comput. Acoust. 2 161
Google Scholar
[24] Jensen F B, Kuperman W A, Portor M B, Schmidt H 2000 Computational Ocean Acoustics (Vol. 2) (New York: American Institute of Physics) p338−358
[25] 段哲民, 尹熙鹏 2020 信号与系统 (第四版) (北京: 电子工业出版社) 第84 页
Duan Z M, Yin X P 2020 Signals and Systems (Vol. 4) (Beijing: Publishing House of Electronics Industry) p84 (in Chinese)
-
图 3 NRL Workshop’93提供的Benchmark标准浅海声速剖面
Fig. 3. NRL Workshop’93 Benchmark standard shallow water sound profile
图 4 环境不确定性对信道传递函数以及声源功率估计的影响 (a) 信道传递函数; (b) 声源功率估计
Fig. 4. Influence of environmental uncertainty on acoustic transfer function and source power estimation: (a) Acoustic transfer function; (b) source power estimation
图 5 海水深度(
$ d_1 $ )变化对各类简正波的影响Fig. 5. Influence of the variation of water depth on different kind of normal mode
图 6 海水声速(
$ c_1, c_2 $ ) 变化对各类简正波的影响 (a)$ c_1 $ 变化; (b)$ c_2 $ 变化Fig. 6. Influence of the variation of sound velocity of water on different kind of normal mode: (a) The variation of
$ c_1 $ ; (b) the variation of$ c_2 $ 
图 7 沉积层声速(
$ c_3, c_4 $ )变化对各类简正波的影响 (a)$ c_3 $ 变化; (b)$ c_4 $ 变化Fig. 7. Influence of the variation of sound velocity of sediment on different kind of normal mode: (a) The variation of
$ c_3 $ ; (b) the variation of$ c_4 $ 
图 8 不同环境参数变化时的声源功率估计结果 (a) 整体图; (b) 局部放大图
Fig. 8. Source power estimation when different environmental parameters change: (a) Overall; (b) partial enlargement
图 9 环境不确定性对不同频率声源功率估计的影响
Fig. 9. Influence of environmental uncertainty on source power estimations at different frequencies
图 10 不同环境参数变化对不同频率声源功率估计的影响 (a) 整体图; (b) 局部放大图
Fig. 10. Influence of different environmental parameters on source power estimations at different frequencies: (a) Overall; (b) partial enlargement
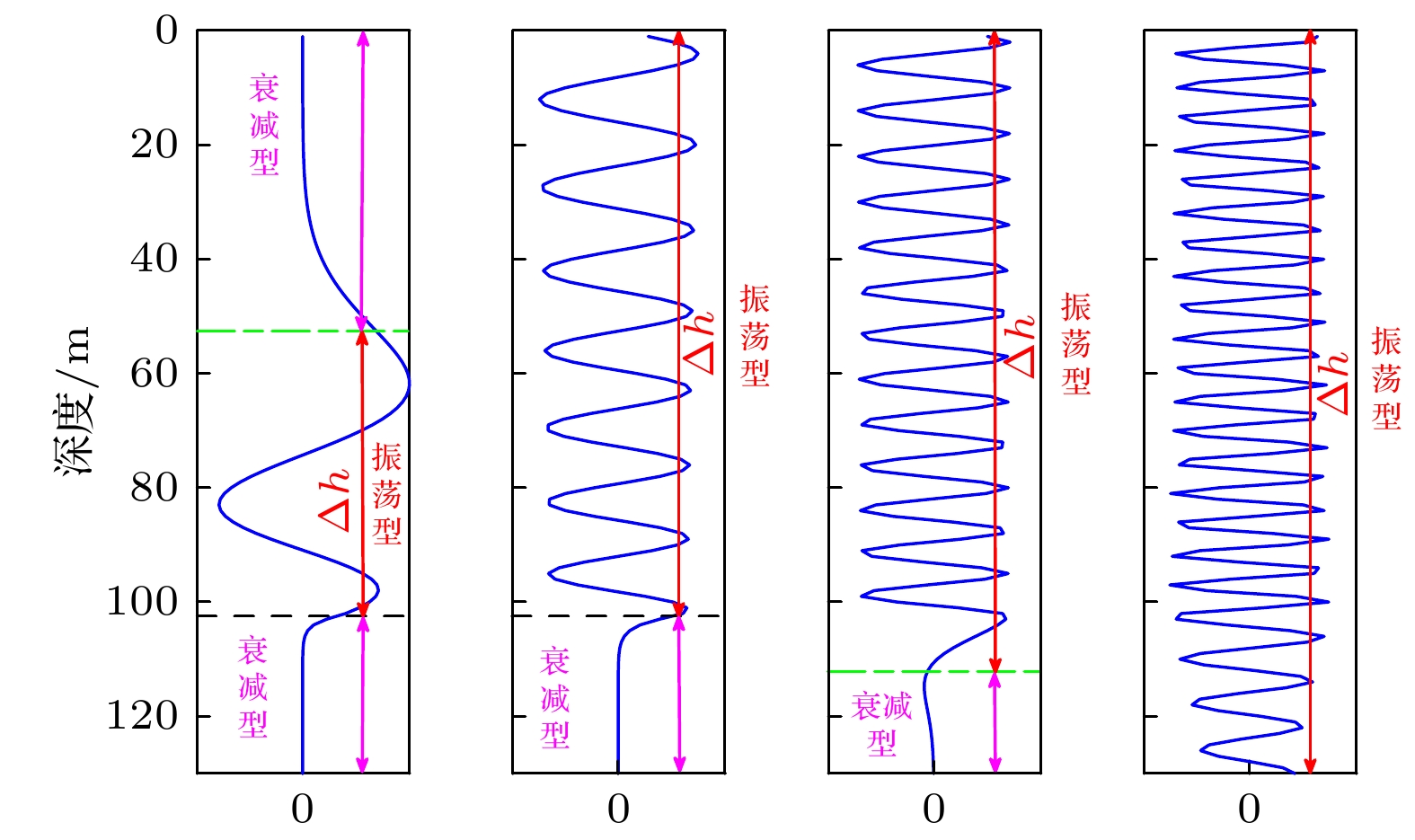
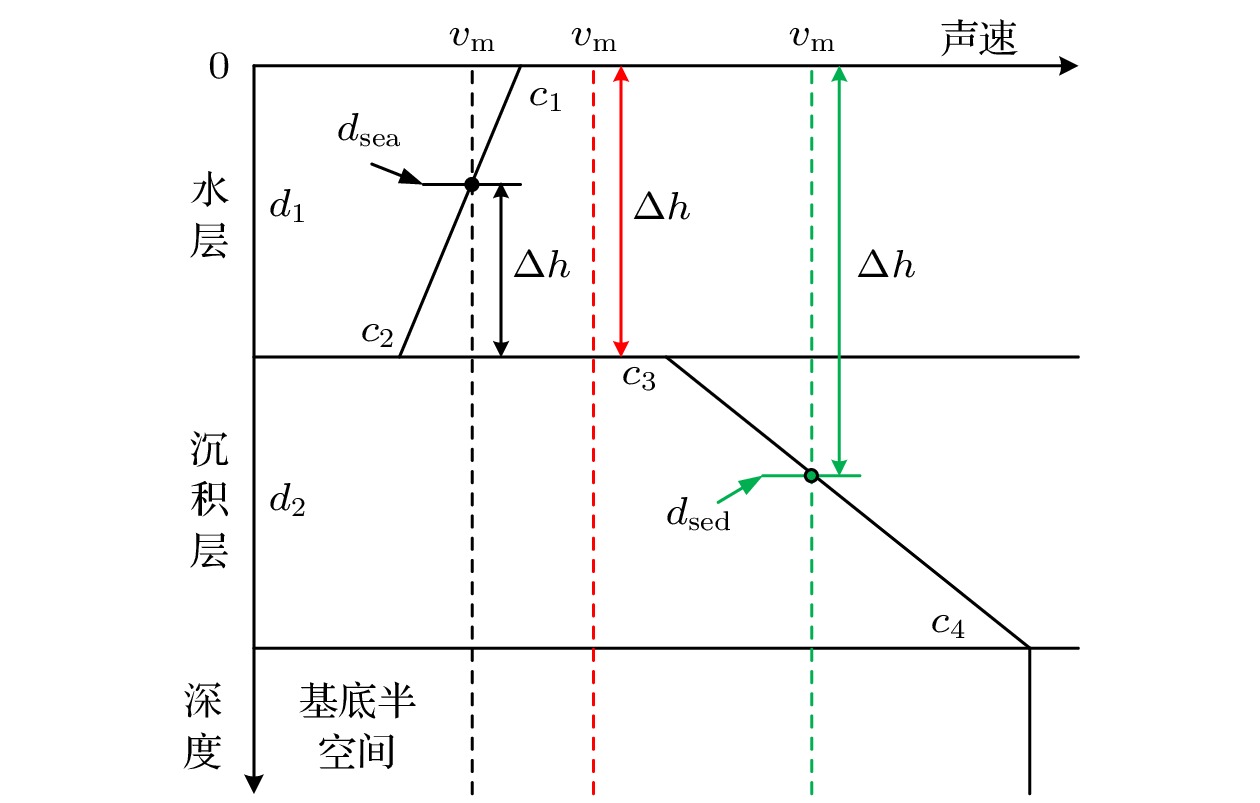
表 1 各类简正波对应的水平波数
$ k_{rm} $ 及可传播深度范围$ \Delta h $ Table 1.
$ k_{rm} $ and$ \Delta h $ of different kind of normal mode简正波类型 $ k_{rm} $ $ \Delta h $ EM $ k_{rm}<\dfrac{\omega}{c_3} $ $ \left[ 0, d_{\mathrm{sed}}\right] $ FPM $\dfrac{\omega}{c_3}\leqslant k_{rm}\leqslant \dfrac{\omega}{c_1}$ $ \left[ 0, d_1\right] $ PPM $\dfrac{\omega}{c_1} < k_{rm}\leqslant \dfrac{\omega}{c_2}$ $ \left[ d_{\mathrm{sea}}, d_1\right] $ 
下载: 导出CSV
表 2 信道传递函数和声源功率估计的统计结果
Table 2. Statistical results of acoustic transfer function and source power estimation
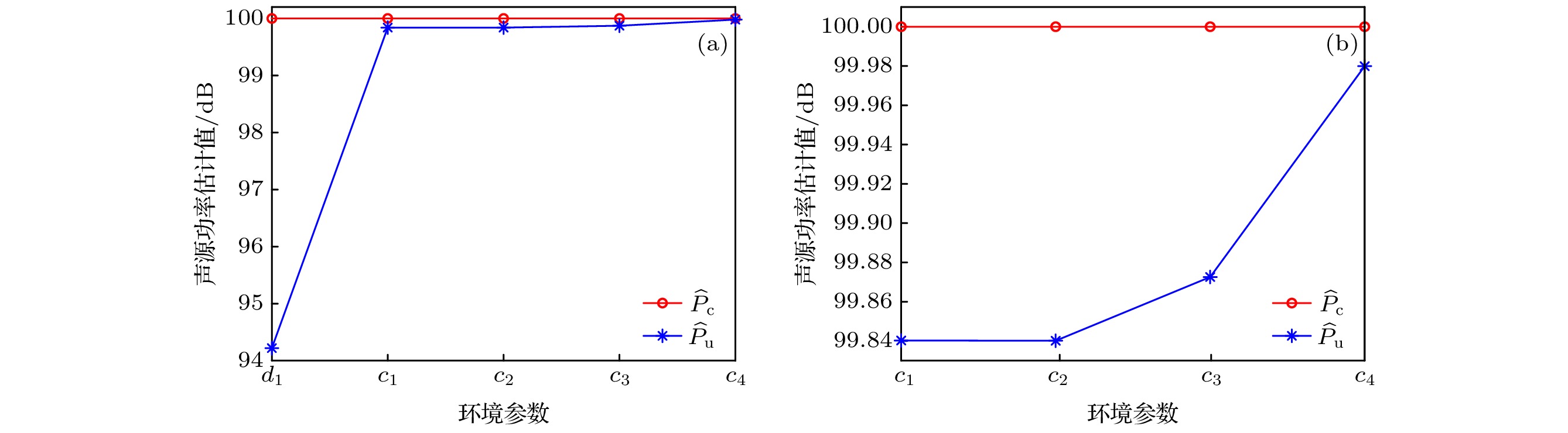
物理量 最大值/dB 最小值/dB 均值/dB 方差 $20\lg\left| D_{\rm{Mod} } \right|$ 0.83 –1.49 –0.11 0.24 $ 20\lg\left| \cos \theta\right| $ –0.02 –30.97 –5.78 28.52 $\hat{P}_{\mathrm{c} }$ 100 100 100 0 $\hat{P}_{\mathrm{u} }$ 100.35 69.73 94.11 28.37 $ S_{\mathrm{em}} $ 0.35 –30.27 –5.89 28.37
下载: 导出CSV
表 3 不同环境参数条件下各类简正波的阶数
Table 3. The number of different kind of normal mode under different environmental parameters
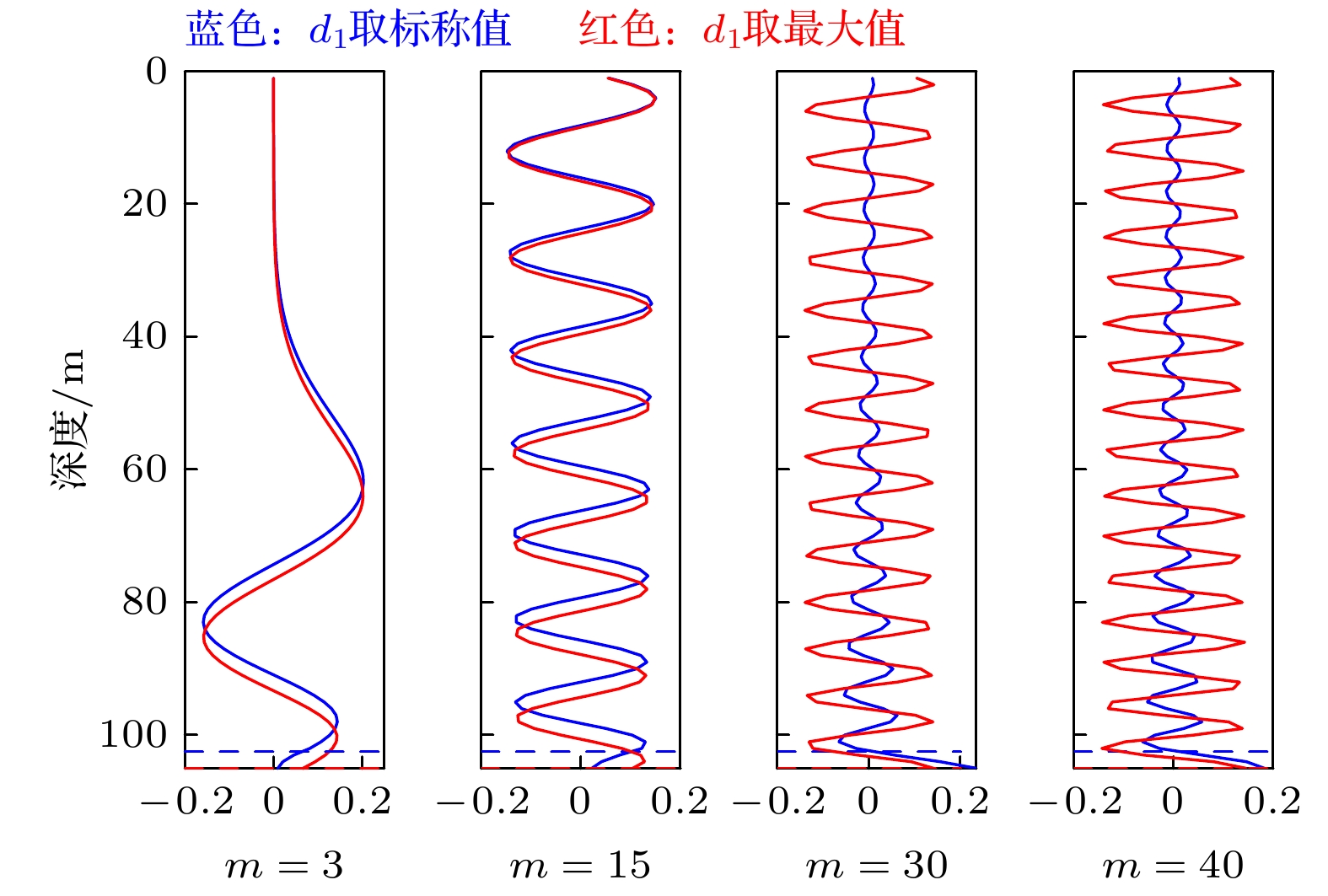
环境参数条件 PPM FPM EM 环境参数均为标称值 1—7 (共7阶) 8—25 (共18阶) 26—127 (共102阶) $ d_1$ = 105 m (最大值) 1—7 (共7阶) 8—26 (共19阶) 27—129 (共103阶) $ c_1 $ = 1502.5 m/s (最大值) 1—8 (共8阶) 9—25 (共17阶) 26—127 (共102阶) $ c_2$ = 1482.5 m/s (最大值) 1—7 (共7阶) 8—25 (共18阶) 26—126 (共101阶) $ c_3 $ = 1650 m/s (最大值) 1—7 (共7阶) 8—30 (共23阶) 31—124 (共94阶) $ c_4 $ = 1850 m/s (最大值) 1—7 (共7阶) 8—25 (共18阶) 26—126 (共101阶)
下载: 导出CSV
-
[1] 蒋国庆, 孙超, 刘雄厚, 蒋光禹 2020 哈尔滨工程大学学报 41 1493
Google Scholar
Jiang G Q, Sun C, Liu X H, Jiang G Y 2020 Journal of Harbin Engineering University 41 1493
Google Scholar
[2] 吴国清, 王美刚, 陈守虎, 马力 2007 声学学报 32 398
Google Scholar
Wu G Q, Wang M G, Chen S H, Ma L 2007 Acta Acustica 32 398
Google Scholar
[3] 高原, 时胜国 2010 声学技术 29 80
Google Scholar
Gao Y, Shi S G 2010 Technical Acoustics 29 80
Google Scholar
[4] 方尔正, 杨德森 2009 声学技术 28 91
Google Scholar
Fang E Z, Yang D S 2009 Technical Acoustics 28 91
Google Scholar
[5] 孙贵青, 杨德森, 张揽月 2002 声学学报 27 429
Google Scholar
Sun G Q, Yang D S, Zhang L Y 2002 Acta Acustica 27 429
Google Scholar
[6] 向龙凤, 孙超 2014 声学学报 39 570
Google Scholar
Xiang L F, Sun C 2014 Acta Acustica 39 570
Google Scholar
[7] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401
Google Scholar
[8] Bucker H P 1976 J. Acoust. Soc. Am. 59 368
Google Scholar
[9] Yang T C 1987 J. Acoust. Soc. Am. 82 1736
Google Scholar
[10] Yang T C 1990 J. Acoust. Soc. Am. 87 2072
Google Scholar
[11] 林建恒, 常道庆, 马力, 李学军, 蒋国健 2001 声学学报 26 217
Google Scholar
Lin J H, Chang D Q, Ma L, Li X J, Jiang G J 2001 Acta Acustica 26 217
Google Scholar
[12] 向龙凤, 孙超, 李明杨 2015 声学学报 40 779
Google Scholar
Xiang L F, Sun C, Li M Y 2015 Acta Acustica 40 779
Google Scholar
[13] Shang E C, Wang Y Y 1991 J. Acoust. Soc. Am. 89 2285
Google Scholar
[14] Del Balzo D R, Feuillade C, Rowe M M 1988 J. Acoust. Soc. Am. 83 2180
Google Scholar
[15] Hamson R M, Heitmeyer R M 1989 J. Acoust. Soc. Am. 86 1950
Google Scholar
[16] Feuillade C, Del Balzo D R, Rowe M M 1989 J. Acoust. Soc. Am. 85 2354
Google Scholar
[17] 赵航芳, 李建龙, 宫先仪 2011 哈尔滨工程大学学报 32 200
Google Scholar
Zhao H F, Li J L, Gong X Y 2011 Journal of Harbin Engineering University 32 200
Google Scholar
[18] 刘宗伟, 孙超, 杜金燕 2013 62 064303
Google Scholar
Liu Z W, Sun C, Du J Y 2013 Acta Phys. Sin. 62 064303
Google Scholar
[19] 李明杨, 孙超, 邵炫 2014 63 204302
Google Scholar
Li M Y, Sun C, Shao X 2014 Acta Phys. Sin. 63 204302
Google Scholar
[20] Dosso S E, Morley M G, Giles P M, Brooke G H, McCammon D F, Pecknold S, Hines P C 2007 J. Acoust. Soc. Am. 122 2560
Google Scholar
[21] 孔德智, 孙超, 李明杨, 卓颉, 刘雄厚 2019 68 174301
Google Scholar
Kong D Z, Sun C, Li M Y, Zhuo J, Liu X H 2019 Acta Phys. Sin. 68 174301
Google Scholar
[22] 贾雨晴, 苏林, 郭圣明, 马力 2018 67 174302
Google Scholar
Jia Y Q, Su L, Guo S M, Ma L 2018 Acta Phys. Sin. 67 174302
Google Scholar
[23] Porter M B, Tolstoy A 1994 J. Comput. Acoust. 2 161
Google Scholar
[24] Jensen F B, Kuperman W A, Portor M B, Schmidt H 2000 Computational Ocean Acoustics (Vol. 2) (New York: American Institute of Physics) p338−358
[25] 段哲民, 尹熙鹏 2020 信号与系统 (第四版) (北京: 电子工业出版社) 第84 页
Duan Z M, Yin X P 2020 Signals and Systems (Vol. 4) (Beijing: Publishing House of Electronics Industry) p84 (in Chinese)
下载:
计量
- 文章访问数: 3735
- PDF下载量: 76
- 被引次数: 0
