-
Laser cooling and trapping of neutral atoms is of great significance for studying the physical and chemical properties of atoms. To further realize the spatial localization of atoms, optical dipole trap (ODT) was proposed to manipulate individual atoms, ions or molecules and has become an increasingly important technique in the field of cold atomic physics and quantum optics. To eliminate the differential light shift of transitions between atomic states, ODT can be turned off during excitation/radiation. However, it will shorten the trap lifetime of the atom and reduce the repetition rate of the single photon. The AC stark shift can be eliminated experimentally by constructing blue-detuned dark ODT, but the micron-level dark ODT usually requires more complex experimental equipment and is not easy to operate. Therefore, magic-wavelength ODT was constructed to realize that the transition frequency of photons between atomic states is the same as in free space. When the trapping laser makes the differential light shift of the transition between the two atomic states zero, the laser wavelength is called the magic wavelength. The magic-wavelength ODT can eliminate the differential light shift of the transition between atoms, improve the repetition rate of the experimental sequence and weaken the atomic decoherence. In recent years, it has become a powerful tool for manipulating cold atoms, especially for coherently manipulating the atomic inner states. In the present work, with the theory of multi-level model, we calculate the dynamic electric polarizability of the 6S1/2 ground state and the 6P3/2 excited state connecting the D2 line of cesium atom in a range of 800–1000 nm, and obtain the magic wavelength of the optical trapping laser to trap the ground state and the excited state. Since the polarizability of atomic states with angular momentum greater than 0.5 is very sensitive to the polarization angle, the polarization-angle-dependent magic wavelength and the corresponding magic polarizability are analyzed by taking the linearly-polarized trapping laser for example. The magic polarization angle is 54.7° and the magic wavelength at this angle are 886.4315 and 934.0641 nm, respectively. The robustness of the magic conditions and the feasibility of the experimental operation are further analyzed.
-
Keywords:
- cesium atomic D2 line /
- dynamic polarizability /
- magic-wavelength optical dipole trap /
- polarization angle
[1] Grimm R, Weidemüller M, Ovchinnikov Y B 2000 Adv. At. Mol. Opt. Phys. 42 95
[2] Monroe C, Swann W, Robinson H, Wieman C 1990 Phys. Rev. Lett. 65 1571
Google Scholar
[3] Barredo D, Lienhard V, Scholl P, de Léséleuc S, Boulier T, Browaeys A, Lahaye T 2020 Phys. Rev. Lett. 124 023201
Google Scholar
[4] He J, Wang J, Yang B D, Zhang T C, Wang J M 2009 Chin. Phys. B 18 3404
Google Scholar
[5] Li G, Zhang S, Isenhower L, Maller K, Saffman M 2012 Opt. Lett. 37 851
Google Scholar
[6] Ye J, Kimble H J, Katori H 2008 Science 320 1734
Google Scholar
[7] Katori H, Ido T, Kuwata-Gonokami M 1999 J. Phys. Soc. Jpn. 68 2479
Google Scholar
[8] McKeever J, Buck J R, Boozer A D, Kuzmich A, Nagerl H C, Stamper-Kurn D M, Kimble H J 2003 Phys. Rev. Lett. 90 133602
Google Scholar
[9] Phoonthong P, Douglas P, Wickenbrock A, Renzoni F 2010 Phys. Rev. A 82 013406
Google Scholar
[10] Liu B, Jin G, Sun R, He J, Wang J M 2017 Opt. Express 25 15861
Google Scholar
[11] Takamoto M, Hong F L, Higashi R, Katori H 2005 Nature 435 321
Google Scholar
[12] Liu P L, Huang Y, Bian W, Shao H, Guan H, Tang Y B, Li C B, Mitroy J, Gao K L 2015 Phys. Rev. Lett. 114 223001
Google Scholar
[13] Huang Y, Guan H, Liu P, Bian W, Ma L, Liang K, Li T, Gao K 2016 Phys. Rev. Lett. 116 013001
Google Scholar
[14] Dörscher S, Huntemann N, Schwarz R, Lange R, Benkler E, Lipphardt B, Sterr U, Peik E, Lisdat C 2021 Metrologia 58 015005
Google Scholar
[15] McFerran J J, Yi L, Mejri S, Di Manno S, Zhang W, Guéna J, Le Coq Y, Bize S 2012 Phys. Rev. Lett. 108 183004
Google Scholar
[16] Wang J M, Cheng Y J, Guo S L, Yang B D, He J 2012 Proc. SPIE 8440 84400Q
Google Scholar
[17] Li G, Tian Y, Wu W, Li S, Li X, Liu Y, Zhang P, Zhang T 2019 Phys. Rev. Lett. 123 253602
Google Scholar
[18] Kien F L, Schneeweiss P, Rauschenbeutel A 2013 Eur. Phys. J. D 67 92
Google Scholar
[19] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B At. Mol. Opt. Phys. 43 202001
Google Scholar
[20] Šibalić N, Pritchard J D, Adams C S, Weatherill K J 2017 Comput. Phys. Commun. 220 319
Google Scholar
[21] Wang J M, Guo S L, Ge Y L, Cheng Y J, Yang B D, He J 2014 J. Phys. B At. Mol. Opt. Phys. 47 095001
Google Scholar
[22] Bai J D, Wang X, Hou X K, Liu W Y, Wang J M 2022 Photonics 9 303
Google Scholar
[23] Gogyan A, Tecmer P, Zawada M 2021 Opt. Express 29 8654
Google Scholar
-
图 1 由单模高斯激光束俘获的单个铯原子示意图. 在铯原子(852.3473 nm) D2线附近934.0641 nm魔术波长处, 6S1/2基态和6P3/2激发态经历相同的光频移Δf1 = Δf2
Figure 1. Diagram of a single cesium atom captured by a single-mode Gaussian laser beam. At the magic wavelength of 934.0641 nm near the cesium atomic (852.3473 nm) D2 line, the 6S1/2 ground state and the 6P3/2 excited state experience the same light shift Δf1 = Δf2.
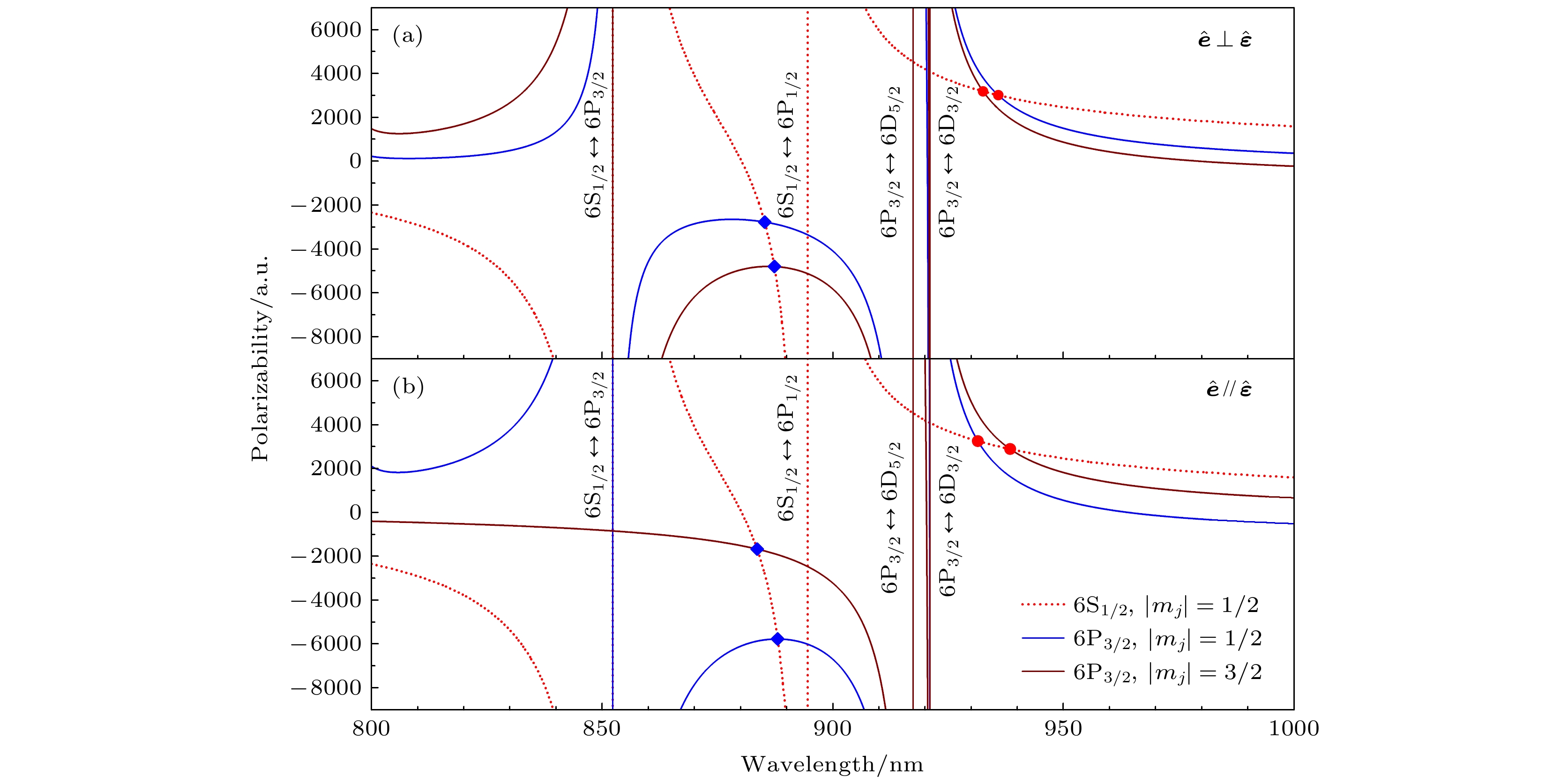
图 2 线偏振光情况下, 铯原子基态(红色虚线)与激发态(实线)的动态极化率(极化率曲线的交点对应的横坐标为魔术波长) (a)量子化轴方向同时垂直于波矢方向和极化矢量方向; (b)量子化轴方向垂直于波矢方向, 平行于极化矢量方向
Figure 2. Dynamic polarizabilities of ground state (red dashed line) and excited state (solid line) of cesium atom for linearly polarized light (The horizontal coordinate corresponding to the intersection of the polarizability curve is called the magic wavelength): (a) The quantized axis is perpendicular to both the wave vector and the polarization vector; (b) the quantized axis is perpendicular to the wave vector and parallel to the polarization vector.
图 3 在6S1/2 ↔ 6P1/2跃迁线附近, (a)魔术波长随极化角的变化关系曲线; (b)在魔术波长位置处, 魔术极化率随极化角的变化关系曲线
Figure 3. Near the 6S1/2 ↔ 6P1/2 transition, (a) the curve of the magic wavelength with the polarization angle; (b) the curve of the magic polarizabitity with the polarization angle at the position of magic wavelength.
图 4 (a) 在6P3/2 ↔ 6D3/2跃迁线附近, 魔术波长随极化角的变化关系曲线; (b) 在魔术波长位置处, 魔术极化率随极化角的变化关系曲线
Figure 4. (a) Near the 6P3/2 ↔ 6D3/2 transition, the curve of the magic wavelength with the polarization angle; (b) the curve of the magic polarizabitity with the polarization angle at the position of magic wavelength.
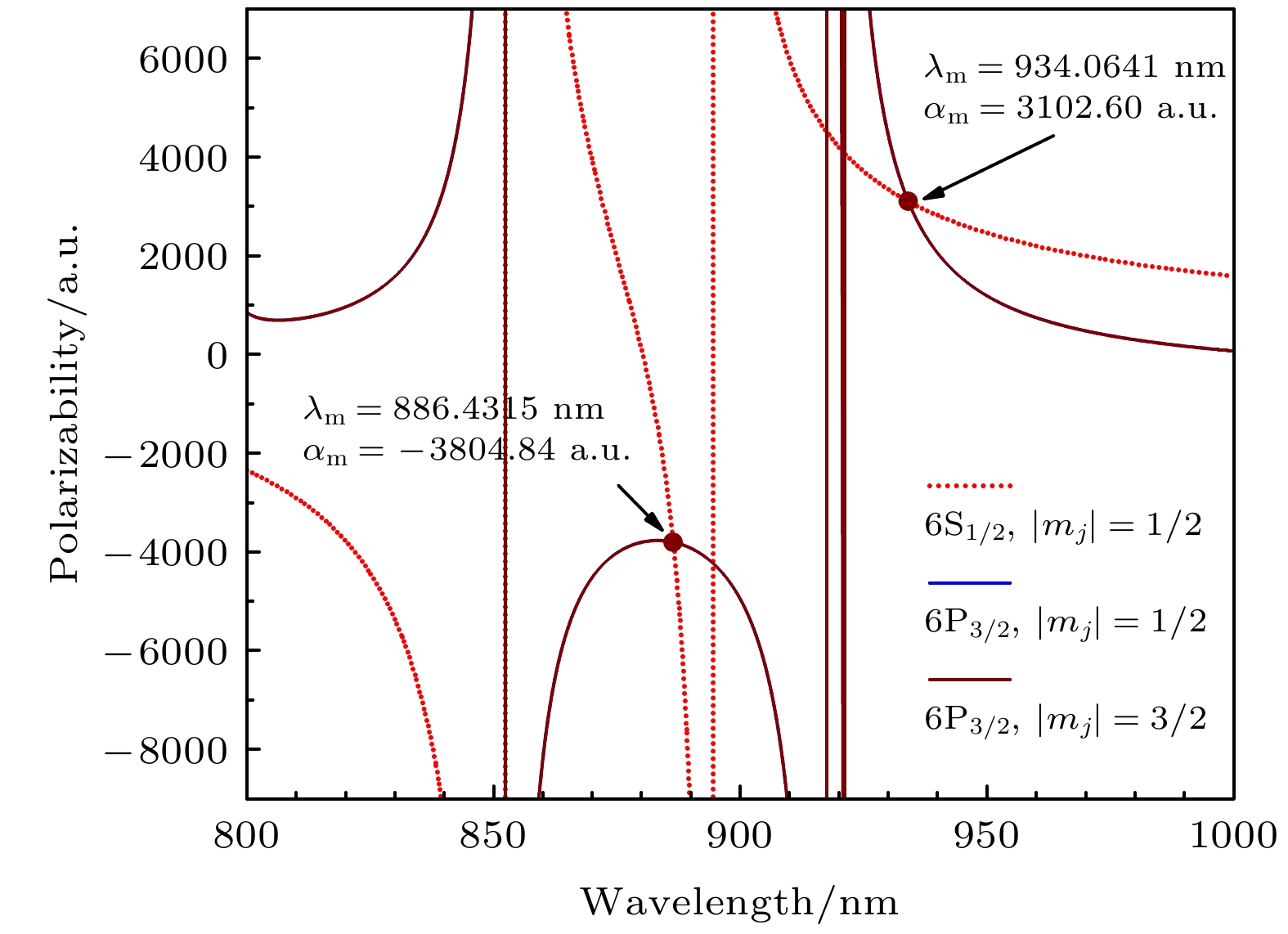
图 5 当极化角为魔术角时, 铯原子基态(红色虚线)与激发态(实线)的动态极化率, 极化率曲线的交点对应的横坐标为魔术波长
Figure 5. Dynamic polarizabilities of ground state (red dashed line) and excited state (solid line) of cesium atom at the magic angle. The horizontal coordinate corresponding to the intersection of the polarizability curve is the magic wavelength.
图 6 当光阱的阱深分别为50Er, 100Er和150Er时, 所需光阱激光的功率随其束腰半径的变化关系
Figure 6. When the well depths of the ODT are 50Er, 100Er, and 150Er, the required power of the ODT laser varies with the beam waist radius.
图 7 针对6S1/2基态和6P3/2激发态的光学偶极阱, 其相对势阱深度随形成光学偶极阱激光波长的变化关系, 其中插图为光阱激光波长在±0.01 nm范围内变化时, 相对势阱深度的变化
Figure 7. For the optical dipole trap of 6S1/2 ground state and 6P3/2 excited state, the relative potential well depth varies with the laser wavelength forming the optical dipole trap. The illustration shows the relative potential well depth varies with the trapping laser wavelength in the range of ±0.01 nm.
图 8 针对6S1/2基态和6P3/2激发态的光学偶极阱, 其相对势阱深度随形成光学偶极阱线偏振激光椭偏度的变化
Figure 8. For the ODT of the 6S1/2 ground state and 6P3/2 excited state, the relative potential well depth varies with the ellipsoid degree of the linearly-polarized laser forming the ODT.
-
[1] Grimm R, Weidemüller M, Ovchinnikov Y B 2000 Adv. At. Mol. Opt. Phys. 42 95
[2] Monroe C, Swann W, Robinson H, Wieman C 1990 Phys. Rev. Lett. 65 1571
Google Scholar
[3] Barredo D, Lienhard V, Scholl P, de Léséleuc S, Boulier T, Browaeys A, Lahaye T 2020 Phys. Rev. Lett. 124 023201
Google Scholar
[4] He J, Wang J, Yang B D, Zhang T C, Wang J M 2009 Chin. Phys. B 18 3404
Google Scholar
[5] Li G, Zhang S, Isenhower L, Maller K, Saffman M 2012 Opt. Lett. 37 851
Google Scholar
[6] Ye J, Kimble H J, Katori H 2008 Science 320 1734
Google Scholar
[7] Katori H, Ido T, Kuwata-Gonokami M 1999 J. Phys. Soc. Jpn. 68 2479
Google Scholar
[8] McKeever J, Buck J R, Boozer A D, Kuzmich A, Nagerl H C, Stamper-Kurn D M, Kimble H J 2003 Phys. Rev. Lett. 90 133602
Google Scholar
[9] Phoonthong P, Douglas P, Wickenbrock A, Renzoni F 2010 Phys. Rev. A 82 013406
Google Scholar
[10] Liu B, Jin G, Sun R, He J, Wang J M 2017 Opt. Express 25 15861
Google Scholar
[11] Takamoto M, Hong F L, Higashi R, Katori H 2005 Nature 435 321
Google Scholar
[12] Liu P L, Huang Y, Bian W, Shao H, Guan H, Tang Y B, Li C B, Mitroy J, Gao K L 2015 Phys. Rev. Lett. 114 223001
Google Scholar
[13] Huang Y, Guan H, Liu P, Bian W, Ma L, Liang K, Li T, Gao K 2016 Phys. Rev. Lett. 116 013001
Google Scholar
[14] Dörscher S, Huntemann N, Schwarz R, Lange R, Benkler E, Lipphardt B, Sterr U, Peik E, Lisdat C 2021 Metrologia 58 015005
Google Scholar
[15] McFerran J J, Yi L, Mejri S, Di Manno S, Zhang W, Guéna J, Le Coq Y, Bize S 2012 Phys. Rev. Lett. 108 183004
Google Scholar
[16] Wang J M, Cheng Y J, Guo S L, Yang B D, He J 2012 Proc. SPIE 8440 84400Q
Google Scholar
[17] Li G, Tian Y, Wu W, Li S, Li X, Liu Y, Zhang P, Zhang T 2019 Phys. Rev. Lett. 123 253602
Google Scholar
[18] Kien F L, Schneeweiss P, Rauschenbeutel A 2013 Eur. Phys. J. D 67 92
Google Scholar
[19] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B At. Mol. Opt. Phys. 43 202001
Google Scholar
[20] Šibalić N, Pritchard J D, Adams C S, Weatherill K J 2017 Comput. Phys. Commun. 220 319
Google Scholar
[21] Wang J M, Guo S L, Ge Y L, Cheng Y J, Yang B D, He J 2014 J. Phys. B At. Mol. Opt. Phys. 47 095001
Google Scholar
[22] Bai J D, Wang X, Hou X K, Liu W Y, Wang J M 2022 Photonics 9 303
Google Scholar
[23] Gogyan A, Tecmer P, Zawada M 2021 Opt. Express 29 8654
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3749
- PDF Downloads: 100
- Cited By: 0
