-
原子线共振波段量子光源的制备在精密测量以及研究非经典光与物质的相互作用方面具有重要意义. 本文报道了在实验上首次利用低于阈值的环形光学参量放大器产生铯原子D2线的明亮偏振压缩光. 实验上利用参量放大过程产生了波长852 nm附近三个斯托克斯参量
$ {\hat S_1} $ ,$ {\hat S_2} $ 和$ {\hat S_3} $ 的偏振压缩光源, 在频率为2—10 MHz范围内, 实测最大压缩达4.3 dB, 考虑探测及传输等因素, 参量放大器出射的压缩为5.2 dB(即标准量子噪声基准的30.2%). 该原子线共振的量子光源在量子存储、光与原子相互作用和超越标准量子极限的精密测量等领域具有重要的应用价值.Quantum light field is very important source in quantum optics and quantum precision measurement, and the generation of quantum state of light is significant in quantum storage, quantum metrology and studying the interaction between nonclassical light and matter. The polarization squeezed light near the atomic transition has great potential applications in the precise measurement of magnetic field as its Stokes parameter’s noise is less than the standard quantum limit (SQL). Therefore, it is very important to generate the polarization squeezed light at atomic transition. We report in this paper the experiment on generating the bright polarization squeezed light at cesium D2 line based on an optical parametric amplifier (OPA). The experimental system includes the following three parts: 1) a second harmonic generator (SHG), 2) an OPA, and 3) a detection system. The OPA has a similar structure to the SHG system with four-mirror ring cavity in which only the fundamental wave is resonant. A nonlinear type-I periodically-poled KTiOPO4 (PPKTP) crystal with a size of 1 mm × 2 mm × 20 mm is placed in the center of the cavity waist and its temperature is precisely controlled. The OPA is pumped by the 426 nm blue light which is generated by SHG and this OPA is operating below the threshold. The squeezed light at cesium D2 line is produced when the crystal temperature is at its optimum phase-matching temperature and the OPA cavity is stabilized based on resonance. The generated squeezed light is combined with the coherent light on a polarizing beam splitter (PBS) to obtain the polarized squeezed light for either${\hat S_2} $ or${\hat S_3} $ of the Stokes parameter by controlling the type of squeezed light (parametric amplification or de-amplification) and the relative phase (0 or π/2) of two beams. And for${\hat S_1} $ , the amplitude-squeezed light (corresponding to parametric de-amplification) is the${\hat S_1} $ squeezed light. The maximum squeezing of 4.3 dB (actually 5.2 dB) is observed in a bandwidth range of 2-10 MHz. At present, the squeezing is mainly limited by the escape efficiency of OPA and the detection efficiency, and the OPA escape efficiency is mainly limited by the blue-light-induced loss of PPKTP crystal and the thermal effect of crystal. In the optical atomic magnetometer, increasing the signal-to-noise ratio (SNR) of the system can effectively improve the sensitivity of the magnetic field measurement. This bright polarization squeezed light is expected to be used in the optical cesium atomic magnetometer to improve the sensitivity of the magnetometer.[1] Appel J, Figueroa E, Korystov D, Lobino M, Lvovsky A I 2008 Phys. Rev. Lett. 100 093602
Google Scholar
[2] Goda K, Miyakawa O, Mikhailov E E, Saraf S, Adhikari R, McKenzie K, Ward R, Vass S, Weinstein A J, Mavalvala N 2008 Nat. Phys. 4 472
Google Scholar
[3] Polzik E S, Carri J, Kimble H J 1992 Phys. Rev. Lett. 68 3020
Google Scholar
[4] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409
Google Scholar
[5] Seshadreesan K P, Anisimov P M, Lee H, Dowling J P 2011 New J. Phys. 13 083026
Google Scholar
[6] Hou L L, Sui Y X, Wang S, Xu X F 2019 Chin. Phys. B 28 044203
Google Scholar
[7] Kr4420 1990 Phys. Rev. A 42 4177
Google Scholar
[8] Gao J R, Cui F Y, Xue C Y, Xie C D, Peng K C 1998 Opt. Lett. 23 870
Google Scholar
[9] Hong C K, Mandel L 1985 Phys. Rev. A 32 974
Google Scholar
[10] Bowen W P, Schnabel R, Bachor H A, Lam P K 2002 Phys. Rev. Lett. 88 093601
Google Scholar
[11] Zhang T C, Hou Z J, Wang J M, Xie C D, Peng K C 1996 Chin. Phys. Lett. 13 734
Google Scholar
[12] Andersen U L, Gehring T, Marquardt C, Leuchs G 2016 Phys. Scr. 91 053001
Google Scholar
[13] Wolfgramm F, Cerè A, Beduini F A, Predojević A, Koschorreck M, Mitchell M W 2010 Phys. Rev. Lett. 105 053601
Google Scholar
[14] Grangier P, Slusher R E, Yurke B, LaPorta A 1987 Phys. Rev. Lett. 59 2153
Google Scholar
[15] Chirkin A S, Orlov A A, Parashchuk D Y 1993 Quantum Electron. 23 870
Google Scholar
[16] Hald J, Sørensen J L, Schori C, Polzik E S 1999 Phys. Rev. Lett. 83 1319
Google Scholar
[17] Wu L, Yan Z H, Liu Y H, Deng R J, Jia X J, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 161102
Google Scholar
[18] Yan Z H, Wu L, Jia X J, Liu Y H, Deng R J, Li S J, Wang H, Xie C D, Peng K C 2017 Nat. Commun. 8 718
Google Scholar
[19] Wen X, Han Y S, Liu J Y, He J, Wang J M 2017 Opt. Express 25 020737
Google Scholar
[20] Heersink J, Gaber T, Lorenz S, Glöckl O, Korolkova N, Leuchs G 2003 Phys. Rev. A 68 013815
Google Scholar
[21] Barreiro S, Valente P, Failache H, Lezama A 2011 Phys. Rev. A 84 033851
Google Scholar
[22] Bowen W P, Treps N, Buchler B C et al. 2003 Phys. Rev. A 67 032302
[23] Agha I H, Messin G, Grangier P 2010 Opt. Express 18 4198
Google Scholar
[24] Matsko A B, Novikova I, Welch G R, Budker D, Kimball D F, Rochester S M 2002 Phys. Rev. A 66 043815
Google Scholar
[25] Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801
Google Scholar
[26] Korolkova N, Leuchs G, Loudon R, Ralph T C, Silberhorn C 2002 Phys. Rev. A 65 052306
Google Scholar
[27] Schnabel R, Bowen W P, Treps N, Ralph T C, Bachor H-A, Lam P K 2003 Phys. Rev. A 67 012316
Google Scholar
[28] 田剑锋 2018 博士学位论文(太原: 山西大学)
Tian J F 2018 Ph. D. Dissertation (Taiyuan: Shanxi University) (in Chinese)
[29] Tian J F, Zuo G H, Zhang Y C, Li G, Zhang P F, Zhang T C 2017 Chin. Phys. B 26 124206
Google Scholar
[30] Tian J F, Yang C, Xue J, Zhang Y C, Li G, Zhang T C 2016 J. Opt. 18 055506
Google Scholar
[31] Boyd G D, Kleinman D A 1968 J. Appl. Phys. 39 3597
Google Scholar
[32] Black E D 2001 Am. J. Phys. 69 79
Google Scholar
[33] Zhang T C, Goh K W, Chou C W, Lodahl P, Kimble H J 2003 Phys. Rev. A 67 033802
Google Scholar
[34] Hansson G, Karlsson H, Wang S, Laurell F 2000 Appl. Opt. 39 5058
Google Scholar
-
图 1 量子化的庞加莱球和斯托克斯参量图示
Fig. 1. Diagrammatic illustration of the quantum Poincaré sphere and Stokes parameters.
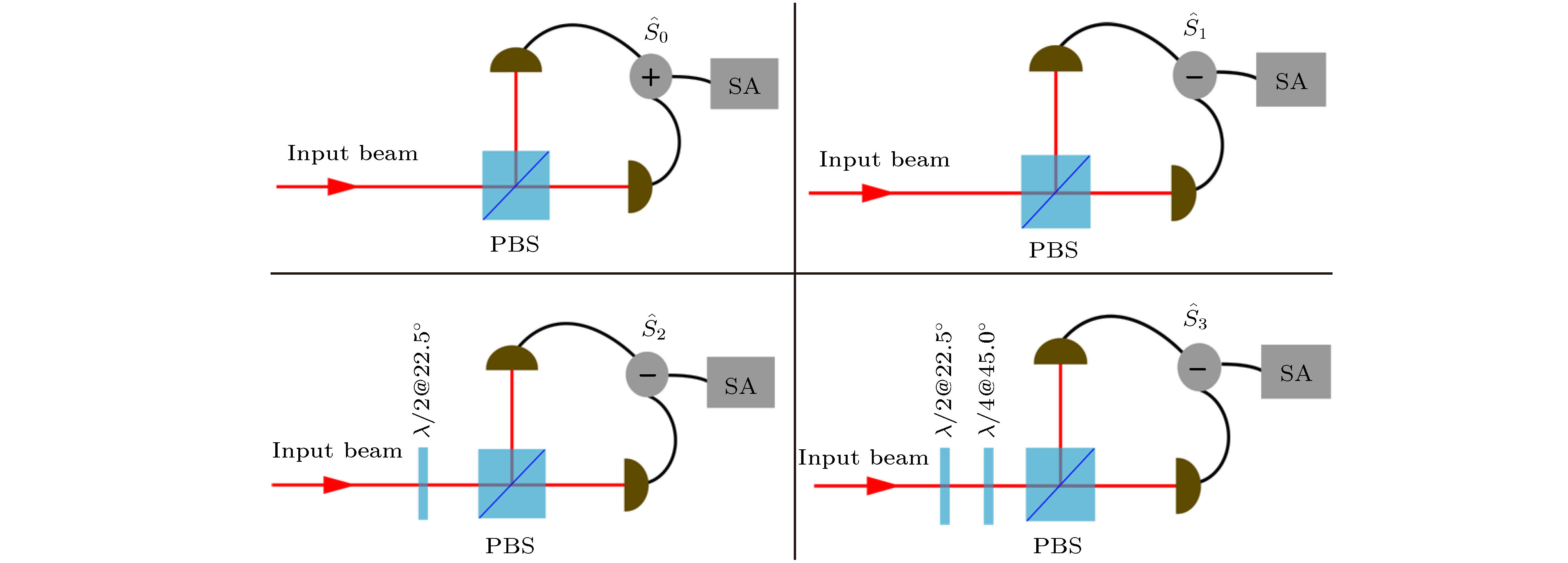
图 2 四个斯托克斯参量的测量装置. PBS, 偏振分束棱镜;
$\lambda /2$ 和$\lambda /4$ 分别是半波片和四分之波片; 加号和减号分别代表电流信号相加减; SA, 频谱分析仪Fig. 2. Apparatus required to measure four Stokes parameters. PBS, polarizing beam splitter;
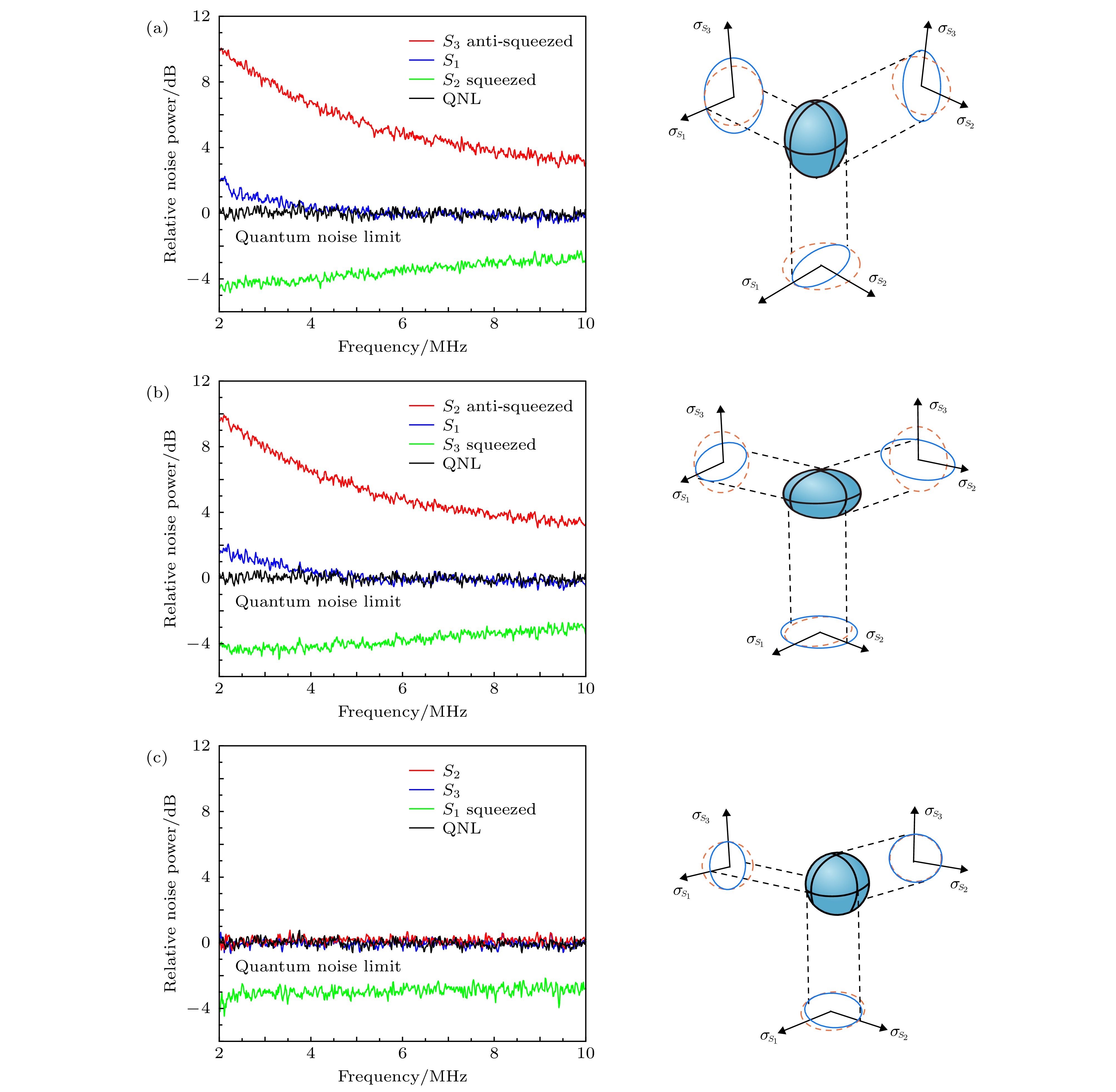
$\lambda /2$ and$\lambda /4$ , half-and quarter-wave plates, respectively; the plus and minus signs imply that an electrical sum or difference has been taken; SA, Spectrum analyzer.
图 3 明亮偏振压缩光合成装置
Fig. 3. Apparatus used to produce the bright polarizationsqueezed beam.
图 5 参量增益随泵浦光功率的变化, 其中绿(红)色实点是参量放大(缩小)的实验结果. 实线是理论拟合结果
Fig. 5. Parametric gain versus pump power, where green (red) solid dots denote the experimental results of amplified (deamplified) gain. The solid lines represent the theoretical results.
图 6 扫描本地光相位时得到的噪声. 谱仪中心频率为2 MHz, 分辨率带宽(RBW)为100 kHz, 视频带宽(VBW)为500 Hz
Fig. 6. Noise power when scanning the local beam phase. The spectrum analyzer’s center frequency is 2 MHz with RBW = 100 kHz and VBW = 500 Hz.
图 7 不同斯托克斯参量的噪声测量结果. 其中左图是测量的斯托克斯参量的噪声谱, 已归一化到标准量子噪声基准. 右图是与之对应的噪声分布球及投影噪声分布, 其中蓝色椭球体代表噪声球, 椭圆表示噪声球投影到各个面上的噪声分布. 红色虚线表示相干光对应的噪声, 蓝色实线表示偏振压缩光 (a)
${\hat S_2}$ 压缩; (b)${\hat S_3}$ 压缩; (c)${\hat S_1}$ 压缩Fig. 7. Measured noise results for different Stokes parameters. The results on the left are the measured variance spectra of Stokes parameters normalized to quantum noise limit. The results on the right are the corresponding diagrammatic illustration of the Stokes parameters’ variance ellipsoid, and the blue ellipsoid is the noise ball, and these ellipses are the noise projections at each plane. The red dashed circles represent the noise of the coherent state and the blue solid circles show the squeezing. (a) Squeezing for Stokes parameter
${\hat S_2}$ ; (b) Squeezing for Stokes parameter${\hat S_3}$ ; (c) Squeezing for Stokes parameter${\hat S_1}$ .表 1 影响OPA产生压缩和探测过程的实验参数
Table 1. Factors of effecting squeezing from the OPA and the detection system.
参数 值 传输效率 0.99 量子效率 0.95 干涉效率 0.986 逃逸率 0.73 归一化泵浦因子 0.71 归一化测量频率 0.18 
下载: 导出CSV
-
[1] Appel J, Figueroa E, Korystov D, Lobino M, Lvovsky A I 2008 Phys. Rev. Lett. 100 093602
Google Scholar
[2] Goda K, Miyakawa O, Mikhailov E E, Saraf S, Adhikari R, McKenzie K, Ward R, Vass S, Weinstein A J, Mavalvala N 2008 Nat. Phys. 4 472
Google Scholar
[3] Polzik E S, Carri J, Kimble H J 1992 Phys. Rev. Lett. 68 3020
Google Scholar
[4] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409
Google Scholar
[5] Seshadreesan K P, Anisimov P M, Lee H, Dowling J P 2011 New J. Phys. 13 083026
Google Scholar
[6] Hou L L, Sui Y X, Wang S, Xu X F 2019 Chin. Phys. B 28 044203
Google Scholar
[7] Kr4420 1990 Phys. Rev. A 42 4177
Google Scholar
[8] Gao J R, Cui F Y, Xue C Y, Xie C D, Peng K C 1998 Opt. Lett. 23 870
Google Scholar
[9] Hong C K, Mandel L 1985 Phys. Rev. A 32 974
Google Scholar
[10] Bowen W P, Schnabel R, Bachor H A, Lam P K 2002 Phys. Rev. Lett. 88 093601
Google Scholar
[11] Zhang T C, Hou Z J, Wang J M, Xie C D, Peng K C 1996 Chin. Phys. Lett. 13 734
Google Scholar
[12] Andersen U L, Gehring T, Marquardt C, Leuchs G 2016 Phys. Scr. 91 053001
Google Scholar
[13] Wolfgramm F, Cerè A, Beduini F A, Predojević A, Koschorreck M, Mitchell M W 2010 Phys. Rev. Lett. 105 053601
Google Scholar
[14] Grangier P, Slusher R E, Yurke B, LaPorta A 1987 Phys. Rev. Lett. 59 2153
Google Scholar
[15] Chirkin A S, Orlov A A, Parashchuk D Y 1993 Quantum Electron. 23 870
Google Scholar
[16] Hald J, Sørensen J L, Schori C, Polzik E S 1999 Phys. Rev. Lett. 83 1319
Google Scholar
[17] Wu L, Yan Z H, Liu Y H, Deng R J, Jia X J, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 161102
Google Scholar
[18] Yan Z H, Wu L, Jia X J, Liu Y H, Deng R J, Li S J, Wang H, Xie C D, Peng K C 2017 Nat. Commun. 8 718
Google Scholar
[19] Wen X, Han Y S, Liu J Y, He J, Wang J M 2017 Opt. Express 25 020737
Google Scholar
[20] Heersink J, Gaber T, Lorenz S, Glöckl O, Korolkova N, Leuchs G 2003 Phys. Rev. A 68 013815
Google Scholar
[21] Barreiro S, Valente P, Failache H, Lezama A 2011 Phys. Rev. A 84 033851
Google Scholar
[22] Bowen W P, Treps N, Buchler B C et al. 2003 Phys. Rev. A 67 032302
[23] Agha I H, Messin G, Grangier P 2010 Opt. Express 18 4198
Google Scholar
[24] Matsko A B, Novikova I, Welch G R, Budker D, Kimball D F, Rochester S M 2002 Phys. Rev. A 66 043815
Google Scholar
[25] Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801
Google Scholar
[26] Korolkova N, Leuchs G, Loudon R, Ralph T C, Silberhorn C 2002 Phys. Rev. A 65 052306
Google Scholar
[27] Schnabel R, Bowen W P, Treps N, Ralph T C, Bachor H-A, Lam P K 2003 Phys. Rev. A 67 012316
Google Scholar
[28] 田剑锋 2018 博士学位论文(太原: 山西大学)
Tian J F 2018 Ph. D. Dissertation (Taiyuan: Shanxi University) (in Chinese)
[29] Tian J F, Zuo G H, Zhang Y C, Li G, Zhang P F, Zhang T C 2017 Chin. Phys. B 26 124206
Google Scholar
[30] Tian J F, Yang C, Xue J, Zhang Y C, Li G, Zhang T C 2016 J. Opt. 18 055506
Google Scholar
[31] Boyd G D, Kleinman D A 1968 J. Appl. Phys. 39 3597
Google Scholar
[32] Black E D 2001 Am. J. Phys. 69 79
Google Scholar
[33] Zhang T C, Goh K W, Chou C W, Lodahl P, Kimble H J 2003 Phys. Rev. A 67 033802
Google Scholar
[34] Hansson G, Karlsson H, Wang S, Laurell F 2000 Appl. Opt. 39 5058
Google Scholar
下载:
计量
- 文章访问数: 9018
- PDF下载量: 112
- 被引次数: 0
