-
Bessel vortex beam, as a typical vortex beam, has the characteristics of carrying orbital angular momentum (OAM), no diffraction, and self-reconstruction, which makes it more competitive than plane wave in the field of future vortex beam target detection and imaging. In order to study the near-field electromagnetic scattering of a vortex beam by a metal target, the expression of the near-scattering field of Bessel vortex beam incident on any metal target is obtained by using the physical optics method, triangular surface element modeling, and the plane wave angular spectrum expansion method of vector Bessel vortex beam. The correctness of the proposed method is verified by comparing with the simulation results of FEKO software. The amplitude distribution and phase distribution of electric field, the OAM spectrum distribution and radar cross section (RCS) of the near-scattering field of the Bessel vortex beam incident on the simple target and the combined target are calculated. The effects of beam parameters, receiving distance, target shape and the positions of beam transmitting and receiving surfaces on near-field scattering results are numerically calculated. In addition, the distributions of near-field OAM spectra under different conditions and the near-field RCS distributions of different targets are given. The numerical results show that the near-field results of Bessel vortex beam incident on metal targets are related to the beam parameters, and conform to the law of Bessel beam changing with parameters. The near-field electric amplitude distribution is affected by the distance between the receiving surface and the target, but the phase distribution is hardly affected. The near-field scattering results reflect the changes of target shape. Under normal incidence, when the target is regular and symmetrical, the amplitude distribution and phase distribution are relatively regular, and the main mode is dominant. When the beam is obliquely incident on or does not fully illuminate the target, the amplitude distribution and phase distribution change, which will lead the derived mode to increase. In particular, when the target and the receiving surface both deviate from the incident beam, the OAM disturbance is the most severe. In the near-field RCS distribution, the RCS distributions of different targets are obviously different, and the results of E plane and H plane are also different. It can be seen from the numerical calculation results that the near-field scattering of Bessel vortex beam by a metal target contains a variety of information. The application of vortex electromagnetic wave will help improve the information acquisition of electromagnetic wave and target detection capability. The results in this work can provide a reference for target imaging and vortex radar detection.
-
Keywords:
- near-field scattering /
- plane wave angular spectrum theory /
- vortex beam /
- orbital angular momentum
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] Mawet D, Riaud P, Absil O, Surdej J 2005 Astrophys. J. 633 1191
Google Scholar
[3] Swartzlander G A, Ford E L, Abdul-Malik R S, Close L M, Peters M A, Palacios D M, Wilson D W 2008 Opt. Express 16 10200
Google Scholar
[4] Arlt J, Dholakia K, Allen L, Padgett M J 1998 J. Modern Opt. 45 1231
[5] Vaziri A, Weihs G, Zeilinger A 2002 J. Optics B 4 S47
Google Scholar
[6] Tamburini F, Mari E, Sponselli A, Thidé B, Bianchini A, Romanato F 2012 New J. Phys. 14 033001
Google Scholar
[7] Tamburini F, Mari E, Thidé B, Barbieri C, Romanato F 2011 Appl. Phys. Lett. 99 204102
Google Scholar
[8] Liu K, Cheng Y Q, Yang Z C, Wang H Q, Qin Y L, Li X 2015 IEEE Antenn. Wirel. Pr. 14 711
Google Scholar
[9] Tang B, Guo K Y, Wang J P, Sheng X Q 2017 IEEE Antenn. Wirel. Pr. 16 2975
Google Scholar
[10] Zhang C, Chen D 2017 IEEE Antenn. Wirel. Pr. 16 2316
Google Scholar
[11] Bu X X, Zhang Z, Chen L Y, Liang X D, Tang H B, Wang X M 2018 IEEE Antenn. Wirel. Pr. 17 764
Google Scholar
[12] Chen H T, Zhang Z Q, Yu J 2020 Appl. Comput. Electrom. 35 129
Google Scholar
[13] Chen Z, Zong X, Zhang Z, Que X, Nie Z 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference Taiyuan, China, July 18–21, 2019 p1
[14] 蒋基恒, 余世星, 寇娜, 丁召, 张正平 2021 70 238401
Google Scholar
Jiang J H, Yu S X, Kou N, Ding Z, Zhang Z P 2021 Acta Phys. Sin. 70 238401
Google Scholar
[15] Nayeri P, Elsherbeni A Z, Yang F 2021 Appl. Comput. Electrom. 28 284
[16] Durnin J 1987 J. Opt. Soc. 4 651
Google Scholar
[17] MacDonald R P, Boothroyd S A, Okamoto T, Chrostowski J, Syrett B A 1996 Opt. Commun. 122 169
Google Scholar
[18] 戴玉蓉, 丁德胜 2011 60 124302
Google Scholar
Dai Y R, Ding D S 2011 Acta Phys. Sin. 60 124302
Google Scholar
[19] Velchev I, Ubachs W 2001 Opt. Lett. 26 530
Google Scholar
[20] Wu Z, Wu J J, Li H Y, Qu T, Meng X S, Xu Q, Wu Z S, Bai J, Yang L, Gong L, Yun Y 2022 IEEE Antenn. Wirel. Pr. 21 1288
Google Scholar
[21] Shao G H, Yan S C, Luo W, Lu G W, Lu Y Q 2017 Sci. Rep. 7 1062
Google Scholar
-
图 1 贝塞尔涡旋波束入射目标的散射几何模型
Figure 1. Geometric model for scattering of the target illuminated by the Bessel vortex beam.
图 2 贝塞尔涡旋波束示意图 (a)—(d) x, y, z方向和总场的电场幅值分布; (e)—(h) x, y, z方向和总场的电场相位分布
Figure 2. Schematic for Bessel vortex beam: (a)–(d) The amplitude distribution of Ex, Ey, Ez and Etotal; (e)–(h) the phase distribution of Ex, Ey, Ez and Etotal.
图 3 目标表面平面子波散射示意图
Figure 3. Schematic for plane wavelet scattering on object surface.
图 4 (a) 平板目标散射示意图; (b) FEKO仿真与本文方法涡旋波退化的幅相分布结果对比
Figure 4. (a) Schematic for the scattering of a plate; (b) comparison between FEKO simulation results and the vortex wave degradation results.
图 5 (a) 球体目标散射示意图; (b) FEKO仿真与本文方法的幅相分布结果对比
Figure 5. (a) Schematic for the scattering of a sphere; (b) comparison between FEKO simulation results and the proposed method.
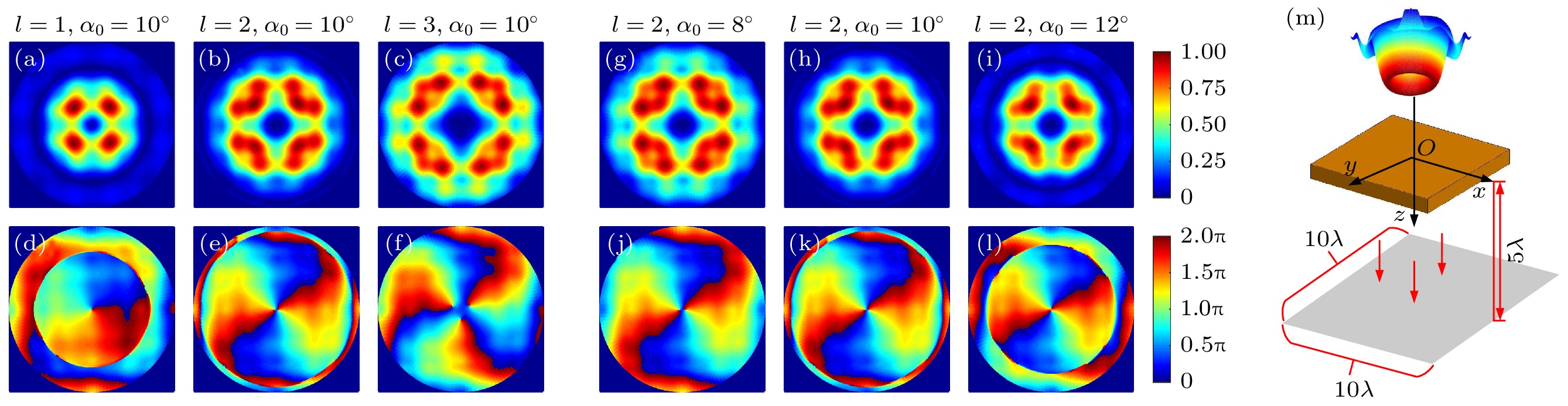
图 6 10 GHz下不同贝塞尔波束参数下的平板近场幅相分布 (a)—(f) 拓扑荷数
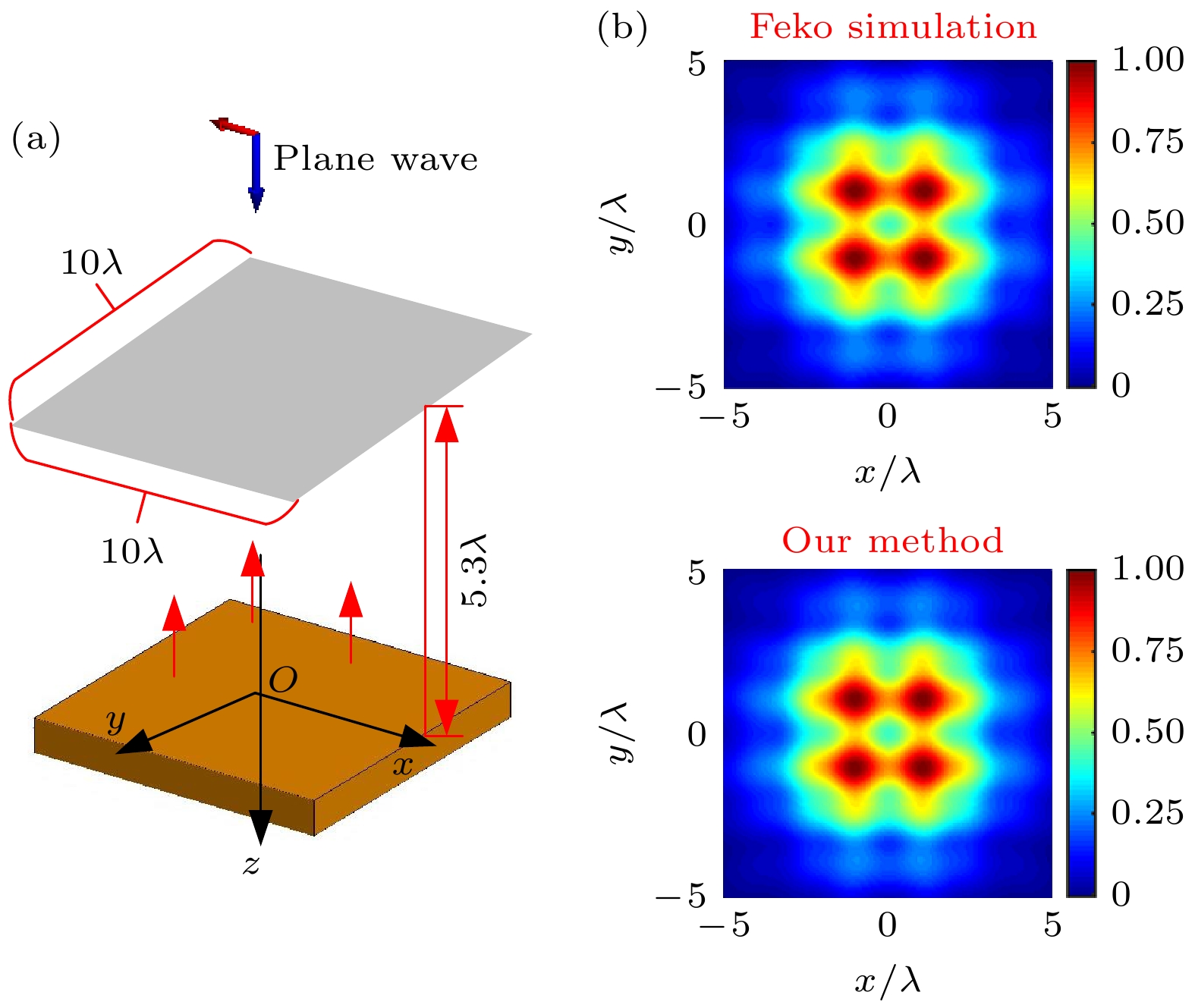
$ l = 1, 2, 3 $ , 半锥角$\alpha_0 = 10^\circ$ ; (g)—(l) 半锥角$\alpha_0 = 8^\circ , 10^\circ , 12^\circ$ , 拓扑荷数$ l = 2 $ ; (m) 平板目标散射示意图Figure 6. Amplitude, phase distribution of scattering near fields with the different Bessel beam parameters at 10 GHz: (a)–(f) Topological charges
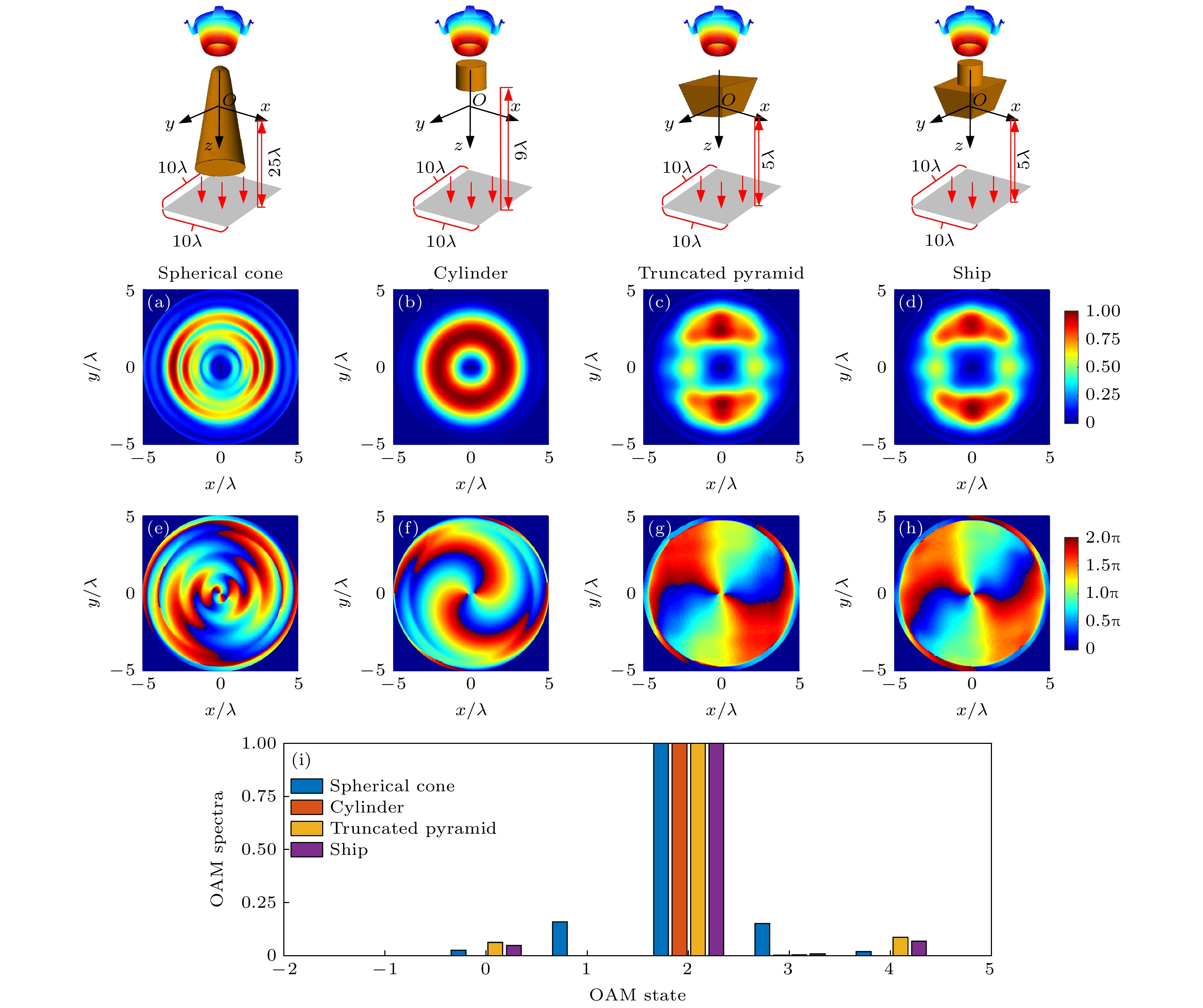
$l = 1,\; 2,\; 3$ , half-cone angle$\alpha_0 = 10^\circ$ ; (g)–(l) half-cone angles$\alpha_0 = 8^\circ , 10^\circ , 12^\circ$ , topological charge$ l = 2 $ ; (m) schematic for the scattering of a flat.
图 7 不同距离的接收面处的散射近场幅相分布 (a), (d) z = 0.15 m; (b), (e) z = 0.21 m; (c), (f) z = 0.27 m
Figure 7. Amplitude and phase distribution of near scattering field at different distances of the receiving surface: (a), (d) z = 0.15 m; (b), (e) z = 0.21 m; (c), (f) z = 0.27 m.
图 8 球锥、圆柱、棱台和船体目标的散射近场的幅相和OAM模态分布 (a)—(d)幅值分布; (e)—(h) 相位分布; (i) OAM模态分布
Figure 8. Amplitude, phase distribution and OAM spectra of the near scattering field of spherical cone, cylinder, truncated pyramid and ship: (a)–(d) Amplitude distributions; (e)–(h) phase distributions; (i) OAM spectra distributions.
图 9 入射角
$ {\theta _0} = 10^\circ $ 时圆柱、棱台和船体目标的散射近场的幅相和OAM模态分布 (a)—(c)幅值分布; (d)—(f)相位分布; (g) OAM模态分布; (h) 散射几何示意图Figure 9. Amplitude, phase distribution and OAM spectra of near scattering field of cylinder, truncated pyramid and ship targets at incidence angle
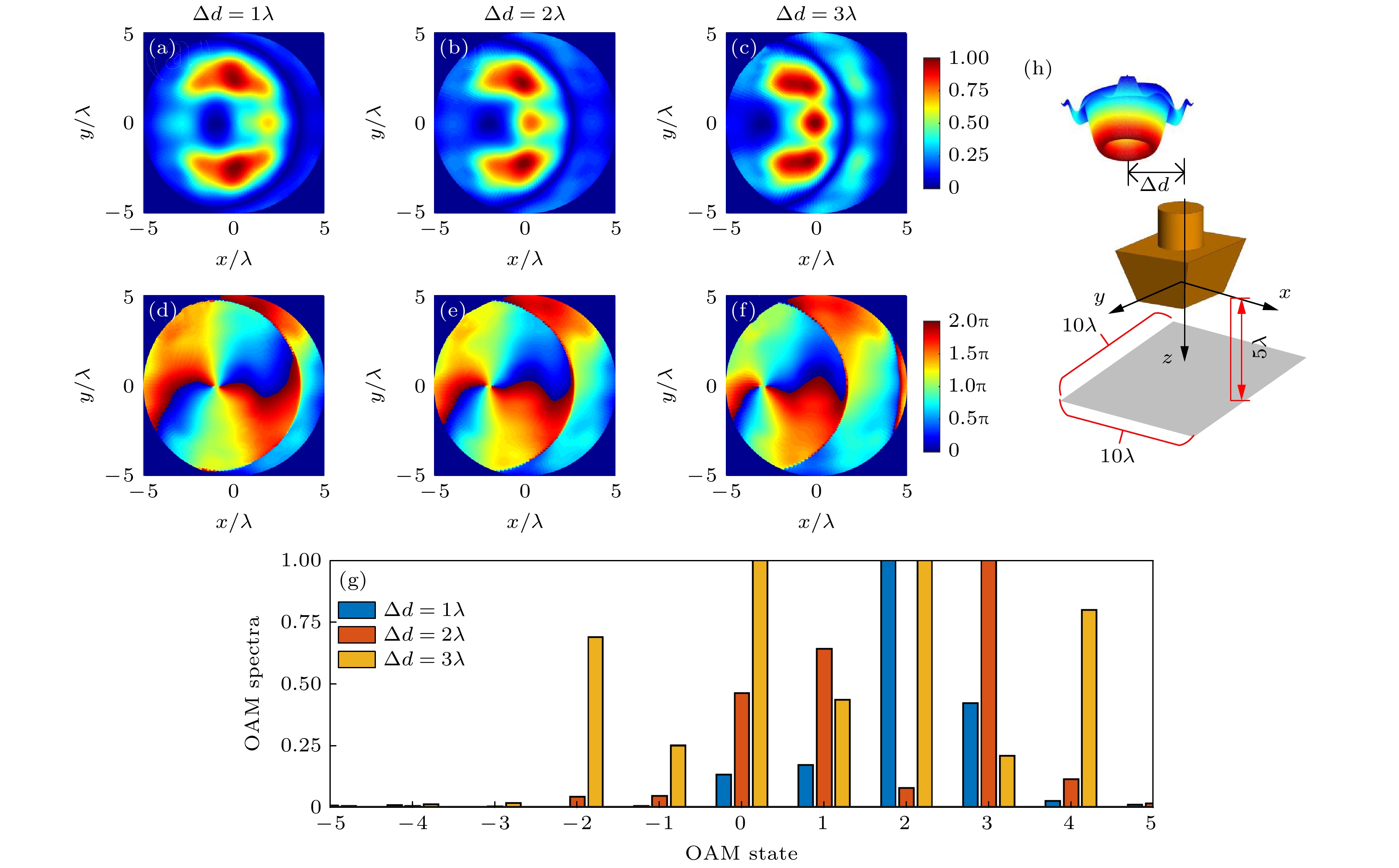
$ {\theta _0} = 10^\circ $ : (a)–(c) Amplitude distribution; (d)–(f) phase distribution; (g) OAM spectra distribution; (h) schematic for target scattering geometry.
图 10 偏移入射波束的船体目标前向散射近场的幅相和OAM模态分布 (a), (d)
$ \Delta d = 1\lambda $ ; (b), (e)$ \Delta d = 2\lambda $ ; (c), (f)$\Delta d = 3\lambda$ ; (g)$ \Delta d = 1\lambda , 2\lambda , 3\lambda $ 时的OAM分布; (h) 目标散射几何示意图Figure 10. Amplitude, phase distribution and OAM spectra of forward near scattering field of ship target with offset incident beam: (a), (d)
$ \Delta d = 1\lambda $ ; (b), (e)$ \Delta d = 2\lambda $ ; (c), (f)$ \Delta d = 3\lambda $ ; (g) OAM spectra at$ \Delta d = 1\lambda , 2\lambda , 3\lambda $ ; (h) schematic for target scattering geometry.
图 11 偏移入射场的船体目标后向散射近场的幅相分布和OAM模态分布 (a), (d)
$ \Delta d = 1\lambda $ ; (b), (e)$ \Delta d = 2\lambda $ ; (c), (f)$\Delta d = $ $ 4\lambda$ ; (g)$\Delta d = 1\lambda , \;2\lambda , \;4\lambda$ 时的OAM分布; (h) 散射几何示意图Figure 11. Amplitude, phase distribution and OAM spectra of the backward near scattering field of a ship target offset by the incident field: (a), (d)
$ \Delta d = 1\lambda $ ; (b), (e)$ \Delta d = 2\lambda $ ; (c), (f)$ \Delta d = 4\lambda $ ; (g) OAM spectra at$\Delta d = 1\lambda ,\; 2\lambda ,\; 4\lambda$ ; (h) schematic for target scattering geometry.
图 12 球锥、圆柱、船体目标散射近场的RCS分布 (a)—(c) RCS分布俯视图; (d)—(f) RCS分布主视图
Figure 12. RCS distribution of the near scattering field of different targets: (a)–(c) Top view of RCS distribution; (d)—(f) front view of RCS distribution.
-
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] Mawet D, Riaud P, Absil O, Surdej J 2005 Astrophys. J. 633 1191
Google Scholar
[3] Swartzlander G A, Ford E L, Abdul-Malik R S, Close L M, Peters M A, Palacios D M, Wilson D W 2008 Opt. Express 16 10200
Google Scholar
[4] Arlt J, Dholakia K, Allen L, Padgett M J 1998 J. Modern Opt. 45 1231
[5] Vaziri A, Weihs G, Zeilinger A 2002 J. Optics B 4 S47
Google Scholar
[6] Tamburini F, Mari E, Sponselli A, Thidé B, Bianchini A, Romanato F 2012 New J. Phys. 14 033001
Google Scholar
[7] Tamburini F, Mari E, Thidé B, Barbieri C, Romanato F 2011 Appl. Phys. Lett. 99 204102
Google Scholar
[8] Liu K, Cheng Y Q, Yang Z C, Wang H Q, Qin Y L, Li X 2015 IEEE Antenn. Wirel. Pr. 14 711
Google Scholar
[9] Tang B, Guo K Y, Wang J P, Sheng X Q 2017 IEEE Antenn. Wirel. Pr. 16 2975
Google Scholar
[10] Zhang C, Chen D 2017 IEEE Antenn. Wirel. Pr. 16 2316
Google Scholar
[11] Bu X X, Zhang Z, Chen L Y, Liang X D, Tang H B, Wang X M 2018 IEEE Antenn. Wirel. Pr. 17 764
Google Scholar
[12] Chen H T, Zhang Z Q, Yu J 2020 Appl. Comput. Electrom. 35 129
Google Scholar
[13] Chen Z, Zong X, Zhang Z, Que X, Nie Z 2019 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference Taiyuan, China, July 18–21, 2019 p1
[14] 蒋基恒, 余世星, 寇娜, 丁召, 张正平 2021 70 238401
Google Scholar
Jiang J H, Yu S X, Kou N, Ding Z, Zhang Z P 2021 Acta Phys. Sin. 70 238401
Google Scholar
[15] Nayeri P, Elsherbeni A Z, Yang F 2021 Appl. Comput. Electrom. 28 284
[16] Durnin J 1987 J. Opt. Soc. 4 651
Google Scholar
[17] MacDonald R P, Boothroyd S A, Okamoto T, Chrostowski J, Syrett B A 1996 Opt. Commun. 122 169
Google Scholar
[18] 戴玉蓉, 丁德胜 2011 60 124302
Google Scholar
Dai Y R, Ding D S 2011 Acta Phys. Sin. 60 124302
Google Scholar
[19] Velchev I, Ubachs W 2001 Opt. Lett. 26 530
Google Scholar
[20] Wu Z, Wu J J, Li H Y, Qu T, Meng X S, Xu Q, Wu Z S, Bai J, Yang L, Gong L, Yun Y 2022 IEEE Antenn. Wirel. Pr. 21 1288
Google Scholar
[21] Shao G H, Yan S C, Luo W, Lu G W, Lu Y Q 2017 Sci. Rep. 7 1062
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3382
- PDF Downloads: 110
- Cited By: 0
