-
Self-testing is the high-level security verification of a claimed quantum device, confirming the quantum states prepared in the device and the measurements performed based solely on the observed statistics. The statistical correlations can realize the self-testing of the quantum system in the preparing-and-measuring scenario. However, most of previous studies focused on the self-testing of shared entangled states between devices, at present only a few researches are presented and the existing work can only simultaneously self-test the states and measurements when some witness inequalities reach a maximum violation. We focus on four-state preparation and the selected scenarios of two measurements. In this scenario, Armin Tavakoli et al. [Tavakoli A, Kaniewski J, Vértesi T, Rosset D, Brunner N 2018 Phys. Rev. A 98 062307] have put forward a criterion based on the dimensional witness violation inequality which can achieve BB84 particles and corresponding Pauli measurements. However, in addition to the maximum violation of the inequality, any statistics with deviation from the maximum deviation cannot be self-tested. Besides, only the BB84 particle preparation and measurements system can be self-tested with that criterion, resulting in a large number of four-state preparation and two measurement systems that cannot be self-tested. Therefore, in this work, in addition to the maximum violation of that dimension inequality, we directly focus on the full observed statistics and further propose some new criteria for self-testing qubit quantum systems in the preparing-and-measiuring scenarios. And the self-testing criteria are proven in an ideal case. We construct a local isometry by using the constructions commonly used in device-independent cases, exchange the target system with the additional system, and realize the self-testing of more qubit state sets and measurement sets than BB84 particles. This meets the requirements for practical experiments to realize various tasks by different quantum state sets. In addition, we perform a robust analysis of the proposed criteria and use fidelity to describe the closeness of the state to the ideal state of the auxiliary system. Finally, an improved dimensional-dependent NPA method is used to optimize the lower bound of the robustness, making the new criteria practical under experimental noise. We use the YALIMP software package in MATLAB and the solver SEDUMI to solve this optimization problem. The present research increases the diversity of qubit state preparations and self-testing of measurement system, which is beneficial to the actual self-testing of different non-entangled single quantum systems.
-
Keywords:
- self testing /
- prepare-and-measurement /
- witness inequality /
- robustness
[1] Acín A, Brunner N, Gisin N, Massar S, Pironio S, Scarani V 2007 Phys. Rev. Lett. 98 230501
Google Scholar
[2] Mayers D, Yao A 2004 Quant. Inf. Comput. 4 273
Google Scholar
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[4] Bell J S 1964 Physics Physique Fizika 1 195
Google Scholar
[5] Brunner N, Cavalcanti D, Pironio S, Scarani V, Wehner S 2014 Rev. Mod. Phys. 86 419
Google Scholar
[6] Pironio S, Acín A, Massar S, de La Giroday A B, Matsukevich D N, Maunz P, Olmschenk S, Hayes D, Luo L, Manning T A, Monroe C 2010 Nature 464 1021
Google Scholar
[7] Liu Y, Zhao Q, Li M H, Guan J Y, Zhang Y, Bai B, Zhang W, Liu W Z, Wu C, Yuan X, Li H, Munro W J, Wang Z, You L, Zhang J, Ma X, Fan J, Zhang Q, Pan J W 2018 Nature 562 548
Google Scholar
[8] Aharon N, Massar S, Pironio S, Silman J 2016 New J. Phys. 18 025014
Google Scholar
[9] Maitra A, Paul G, Roy S 2017 Phys. Rev. A 95 042344
Google Scholar
[10] Gheorghiu A, Kashefi E, Wallden P 2015 New J. Phys. 17 083040
Google Scholar
[11] Bancal J D, Navascués M, Scarani V, Vértesi T, Yang T H, 2015 Phys. Rev. A 91 022115
Google Scholar
[12] Wang Y K, Wu X Y, Scarani V 2016 New J. Phys. 18 025021
Google Scholar
[13] Pál K F, Vértesi T, Navascués M 2014 Phys. Rev. A 90 042340
Google Scholar
[14] Baccari F, Augusiak R, Šupić I, Tura J, Acín A 2020 Phys. Rev. Lett. 124 020402
Google Scholar
[15] Šupić I, Bowles J 2020 Quantum 4 337
Google Scholar
[16] Li X H, Wang Y K, Han Y G, Qin S J, Gao F and Wen Q Y 2020 IEEE J. Sel. Areas Commun. 38 589
Google Scholar
[17] Coladangelo A, Goh K T, Scarani V 2017 Nat. Commun. 8 15485
Google Scholar
[18] Šupić I, Hoban M J 2016 New J. Phys. 18 075006
Google Scholar
[19] Tavakoli A, Kaniewski J, Vértesi T, Rosset D, Brunner N 2018 Phys. Rev. A 98 062307
Google Scholar
[20] Ambainis A, Leung D, Mancinska L, Ozols M 2008 arXiv: 0810.2937
[21] Hayashi M, Iwama K, Nishimura H, Raymond R, Yamashita S 2006 New J. Phys. 8 129
Google Scholar
[22] Pawłowski M, Brunner N 2011 Phys. Rev. A 84 010302(R
Google Scholar
[23] Li H W, Pawłowski M, Yin Z Q, Guo G C, Han Z F 2012 Phys. Rev. A 85 052308
Google Scholar
[24] Masanes L 2003 arXiv: quant-ph/0309137 [quant-ph]
[25] Masanes L 2005 arXiv: quant-ph/0512100 [quant-ph]
[26] McKague M, Yang T H, Scarani V 2012 J. Phys. A Math. Theor. 45 455304
Google Scholar
[27] Yang T H, Vértesi T, Bancal J D, Scarani V, Navascués M 2014 Phys. Rev. Lett. 113 040401
Google Scholar
[28] Scarani V 2012 Acta Phys. Slovaca. 62 347
Google Scholar
[29] Wu X Y, Cai Y, Yang T H, Le H N, Bancal J D, and Scarani V 2014 Phys. Rev. A 90 042339
Google Scholar
[30] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[31] Navascués M, Pironio S, Acín A 2007 Phys. Rev. Lett. 98 010401
Google Scholar
[32] Navascués M, Pironio S, Acín A 2008 New J. Phys. 10 073013
Google Scholar
[33] Navascués M, de la Torre G, Vértesi T 2014 Phys. Rev. X 4 011011
Google Scholar
[34] Navascués M, Vértesi T 2015 Phys. Rev. Lett. 115 020501
Google Scholar
[35] Li H W, Mironowicz P, Pawłowski M, Yin Z Q, Wu Y C, Wang S, Chen W, Hu H G, Guo G C, Han Z F 2013 Phys. Rev. A 87 020302(R
Google Scholar
[36] Mironowicz P, Li H W, Pawłowski M 2014 Phys. Rev. A 90 022322
Google Scholar
[37] Lofberg J YALMIP: A Toolbox for Modeling and Optimization in MATLAB, Proceedings of the CACSD Conference Taipei, China, September 24, 2004
[38] Sturm J F 1999 Optim. Methods Softw. 11 625
Google Scholar
-
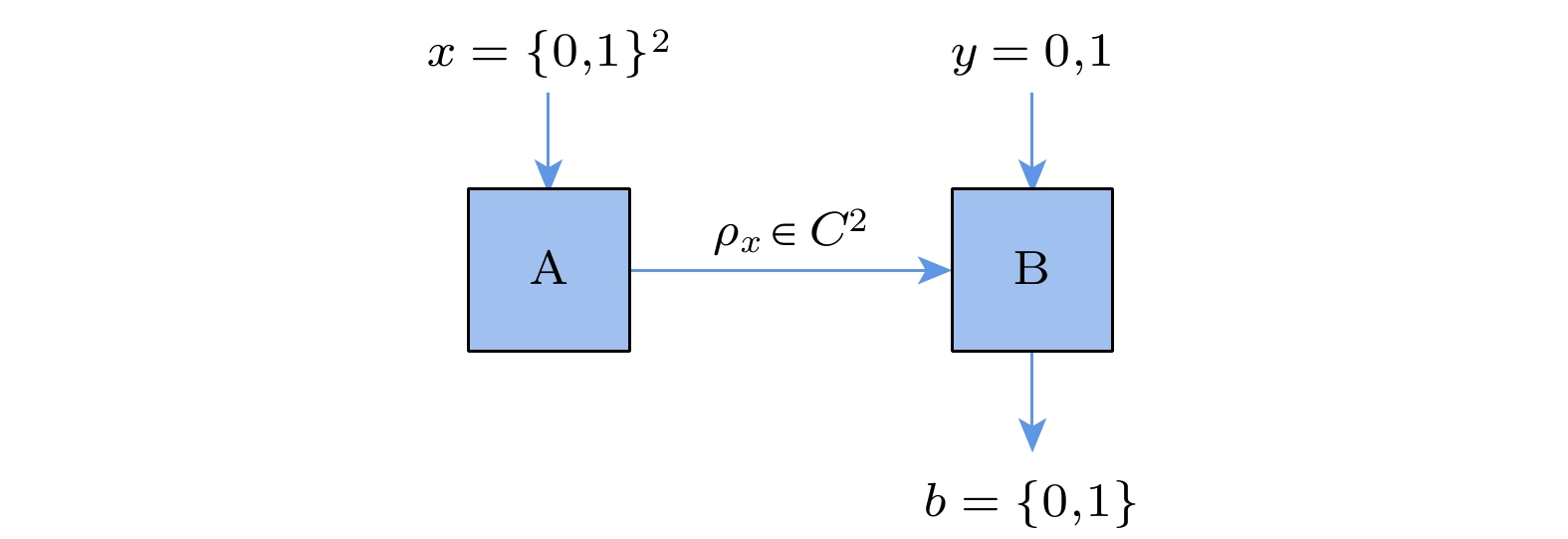
图 1 制备测量量子系统示意图, 其中Alice一侧随机制备4个量子态由x来控制态的选择; Bob一侧随机从两个测量基中进行选择, 以测量发送来的量子态, 由y控制
Figure 1. Schematic diagram of the preparation measurement quantum system, in which four quantum states are randomly prepared on Alice’s site and x controls the selection of states. The measurements in Bob’s site are randomly selected from two measurement bases with y.
图 2 允许对制备状态和相应测量操作进行自测试的局域同构映射,
$ H $ 为哈达玛门,$ Z $ 和$ X $ 为与泡利$ {\sigma }_{x} $ ,$ {\sigma }_{z} $ 门局域等价的门,${\left|0\right.\rangle}_{{\rm{a}}{\rm{n}}{\rm{c}}{\rm{i}}{\rm{l}}{\rm{l}}{\rm{a}}}$ 是辅助系统, 具有所需自测试系统的正确维度, 并将输入态系统记为主(Main)系统Figure 2. The local isometry for the prepared states and corresponding measurements.
$ H $ is the Hadamar gate,$ Z $ and$ X $ is the locally equivalent gate to the Pauli gate$ {\sigma }_{x}, {\sigma }_{z} $ .${\left|0\right.\rangle}_{{\rm{a}}{\rm{n}}{\rm{c}}{\rm{i}}{\rm{l}}{\rm{l}}{\rm{a}}}$ is ancilla system, which has the correct dimensions for the system to be self-tested, and the input-state system is labeled as the Main system.
图 3 t
${\rm{和}}{t}'$ 行的态及测量操作所对应方向的空间位置关系Figure 3. The spatial position relation of the states and the measurements directions in t and
${t}'$ rows.
图 4 单态保真度
$ F $ 的下限. 在相关性误差为$ \varepsilon $ 时, 4种自测试标准的鲁棒性$(\theta ={\text{π}}/2, {\alpha }_{00}={\text{π}}/4, {\alpha }_{01}={\text{π}}/4, 2{\text{π}}/3,$ $7{\text{π}}/12, {\text{π}}/2)$ Figure 4. Lower bound for the certifiable singlet fidelity F as a function of the imperfection of the observed correlations ε. We plot the bounds for four-setting criteria
$(\theta ={\text{π}}/2, {\alpha }_{00}= $ $ {\text{π}}/4, {\alpha }_{01}={\text{π}}/4, 2{\text{π}}/3, 7{\text{π}}/12, {\text{π}}/2)$ .表 1 QRAC实验中统计值
$ {\rm{t}}{\rm{r}}\left({\rho }_{00}{M}_{y}\right) $ 在Bloch球上的表示Table 1. The Bloch sphere expression of the value of
$ {\rm{t}}{\rm{r}}\left({\rho }_{00}{M}_{y}\right) $ in QRAC experiment制备态 测量基 $ {M}_{0} $ $ {M}_{1} $ $ {\rho }_{00} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{00}{M}_{0}\right)={\boldsymbol{r}}_{00}\cdot {\boldsymbol{b}}_{0} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{00}{M}_{1}\right)={\boldsymbol{r}}_{00}\cdot {\boldsymbol{b}}_{1} $ $ {\rho }_{01} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{01}{M}_{0}\right)={\boldsymbol{r}}_{01}\cdot {\boldsymbol{b}}_{0} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{01}{M}_{1}\right)={\boldsymbol{r}}_{01}\cdot {\boldsymbol{b}}_{1} $ $ {\rho }_{10} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{10}{M}_{0}\right)={\boldsymbol{r}}_{10}\cdot {\boldsymbol{b}}_{0} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{10}{M}_{1}\right)={\boldsymbol{r}}_{10}\cdot {\boldsymbol{b}}_{1} $ $ {\rho }_{11} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{11}{M}_{0}\right)={\boldsymbol{r}}_{11}\cdot {\boldsymbol{b}}_{0} $ $ {\rm{t}}{\rm{r}}\left({\rho }_{11}{M}_{1}\right)={\boldsymbol{r}}_{11}\cdot {\boldsymbol{b}}_{1} $ 
DownLoad: CSV
-
[1] Acín A, Brunner N, Gisin N, Massar S, Pironio S, Scarani V 2007 Phys. Rev. Lett. 98 230501
Google Scholar
[2] Mayers D, Yao A 2004 Quant. Inf. Comput. 4 273
Google Scholar
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[4] Bell J S 1964 Physics Physique Fizika 1 195
Google Scholar
[5] Brunner N, Cavalcanti D, Pironio S, Scarani V, Wehner S 2014 Rev. Mod. Phys. 86 419
Google Scholar
[6] Pironio S, Acín A, Massar S, de La Giroday A B, Matsukevich D N, Maunz P, Olmschenk S, Hayes D, Luo L, Manning T A, Monroe C 2010 Nature 464 1021
Google Scholar
[7] Liu Y, Zhao Q, Li M H, Guan J Y, Zhang Y, Bai B, Zhang W, Liu W Z, Wu C, Yuan X, Li H, Munro W J, Wang Z, You L, Zhang J, Ma X, Fan J, Zhang Q, Pan J W 2018 Nature 562 548
Google Scholar
[8] Aharon N, Massar S, Pironio S, Silman J 2016 New J. Phys. 18 025014
Google Scholar
[9] Maitra A, Paul G, Roy S 2017 Phys. Rev. A 95 042344
Google Scholar
[10] Gheorghiu A, Kashefi E, Wallden P 2015 New J. Phys. 17 083040
Google Scholar
[11] Bancal J D, Navascués M, Scarani V, Vértesi T, Yang T H, 2015 Phys. Rev. A 91 022115
Google Scholar
[12] Wang Y K, Wu X Y, Scarani V 2016 New J. Phys. 18 025021
Google Scholar
[13] Pál K F, Vértesi T, Navascués M 2014 Phys. Rev. A 90 042340
Google Scholar
[14] Baccari F, Augusiak R, Šupić I, Tura J, Acín A 2020 Phys. Rev. Lett. 124 020402
Google Scholar
[15] Šupić I, Bowles J 2020 Quantum 4 337
Google Scholar
[16] Li X H, Wang Y K, Han Y G, Qin S J, Gao F and Wen Q Y 2020 IEEE J. Sel. Areas Commun. 38 589
Google Scholar
[17] Coladangelo A, Goh K T, Scarani V 2017 Nat. Commun. 8 15485
Google Scholar
[18] Šupić I, Hoban M J 2016 New J. Phys. 18 075006
Google Scholar
[19] Tavakoli A, Kaniewski J, Vértesi T, Rosset D, Brunner N 2018 Phys. Rev. A 98 062307
Google Scholar
[20] Ambainis A, Leung D, Mancinska L, Ozols M 2008 arXiv: 0810.2937
[21] Hayashi M, Iwama K, Nishimura H, Raymond R, Yamashita S 2006 New J. Phys. 8 129
Google Scholar
[22] Pawłowski M, Brunner N 2011 Phys. Rev. A 84 010302(R
Google Scholar
[23] Li H W, Pawłowski M, Yin Z Q, Guo G C, Han Z F 2012 Phys. Rev. A 85 052308
Google Scholar
[24] Masanes L 2003 arXiv: quant-ph/0309137 [quant-ph]
[25] Masanes L 2005 arXiv: quant-ph/0512100 [quant-ph]
[26] McKague M, Yang T H, Scarani V 2012 J. Phys. A Math. Theor. 45 455304
Google Scholar
[27] Yang T H, Vértesi T, Bancal J D, Scarani V, Navascués M 2014 Phys. Rev. Lett. 113 040401
Google Scholar
[28] Scarani V 2012 Acta Phys. Slovaca. 62 347
Google Scholar
[29] Wu X Y, Cai Y, Yang T H, Le H N, Bancal J D, and Scarani V 2014 Phys. Rev. A 90 042339
Google Scholar
[30] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
Google Scholar
[31] Navascués M, Pironio S, Acín A 2007 Phys. Rev. Lett. 98 010401
Google Scholar
[32] Navascués M, Pironio S, Acín A 2008 New J. Phys. 10 073013
Google Scholar
[33] Navascués M, de la Torre G, Vértesi T 2014 Phys. Rev. X 4 011011
Google Scholar
[34] Navascués M, Vértesi T 2015 Phys. Rev. Lett. 115 020501
Google Scholar
[35] Li H W, Mironowicz P, Pawłowski M, Yin Z Q, Wu Y C, Wang S, Chen W, Hu H G, Guo G C, Han Z F 2013 Phys. Rev. A 87 020302(R
Google Scholar
[36] Mironowicz P, Li H W, Pawłowski M 2014 Phys. Rev. A 90 022322
Google Scholar
[37] Lofberg J YALMIP: A Toolbox for Modeling and Optimization in MATLAB, Proceedings of the CACSD Conference Taipei, China, September 24, 2004
[38] Sturm J F 1999 Optim. Methods Softw. 11 625
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3846
- PDF Downloads: 87
- Cited By: 0
