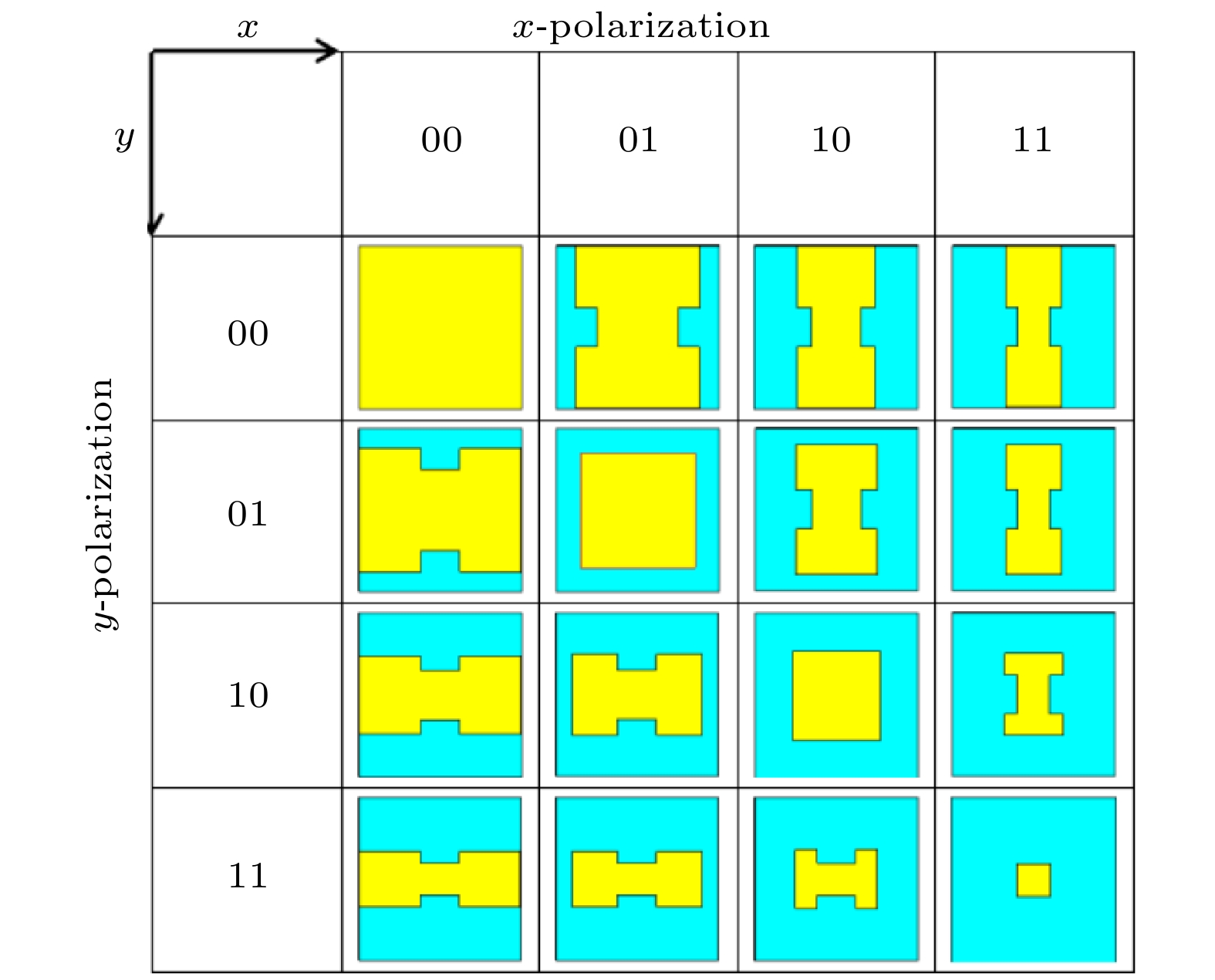
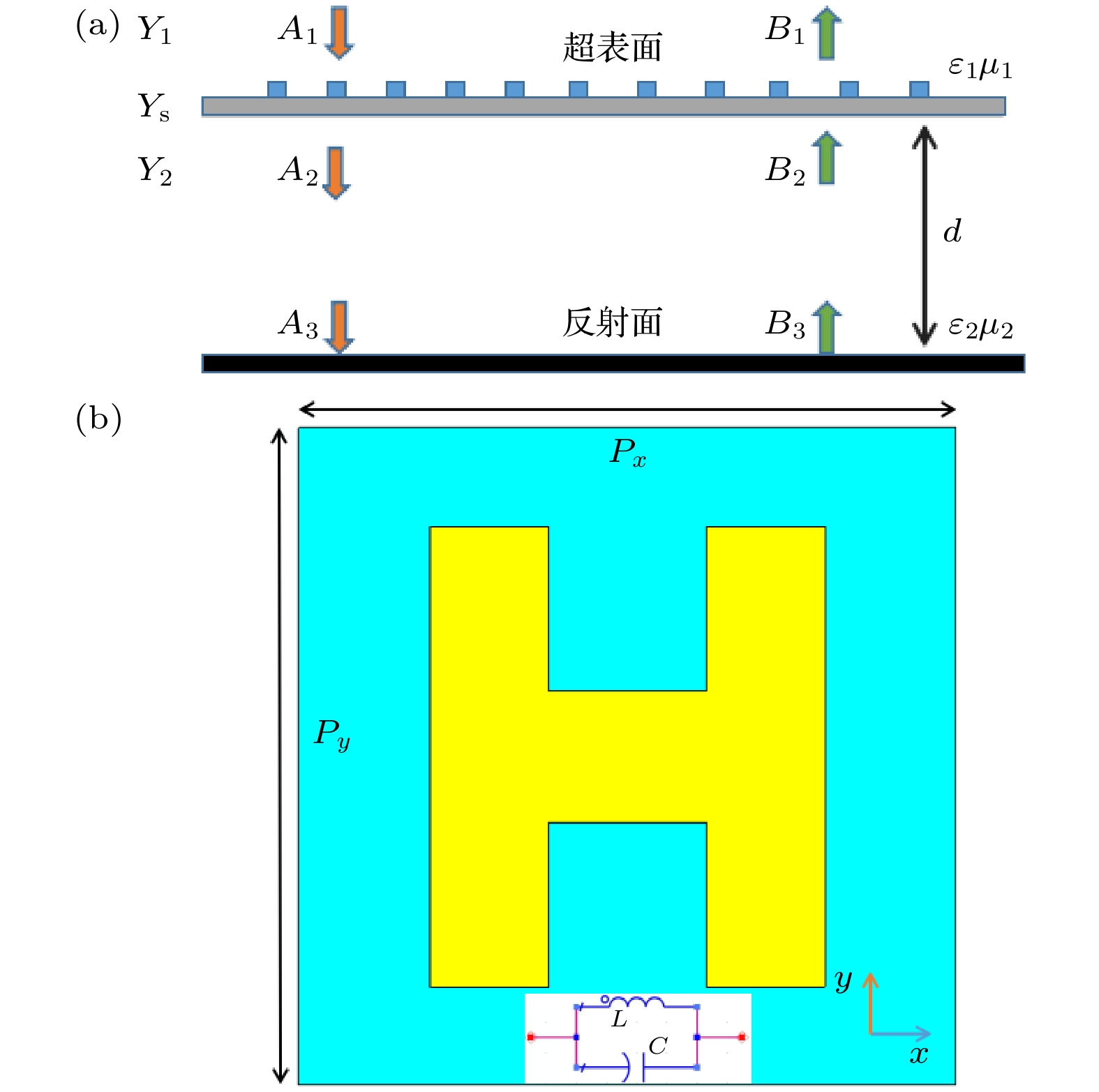
-
本文提出了一个超薄的4-bit双极化编码超表面, 通过正交线极化波的独立操控来实现双模式涡旋波束的生成. 提出的超表面从顶至下依次由“H”形的金属贴片、介质基板层和金属接地层组成. 为了证明所提出的概念, 设计并制造了一个编码超表面. 制造的编码超表面, 在正交线极化波的入射下被设计为携带不同拓扑荷的涡旋波束, 工作中心频率为24.0 GHz. 实验测试结果表明, 理论设计与仿真结果吻合, 从而证实了所提出的4-bit双极化编码超表面具有生成双模式涡旋波束的能力. 这种超薄双模式涡旋生成器有着广泛的应用前景, 特别是在图像和微波领域的无线通信系统中.In this paper, a dual-polarization 4-bit coding metasurface is proposed to achieve the flexible manipulation of different polarization electromagnetic wave reflection angles and the generation of dual-mode vortex beams by independent manipulation of orthogonal linearly polarized waves. The proposed metasurface is composed of an H-type metal patch, dielectric substrate, and metal grounding layer from top to bottom. To prove the proposed concept, we design and fabricate four coding metasurfaces based on the superposition theorem and holographic theory. One of the coding metasurfaces is designed to verify the ability to manipulate the beam angle, and each of the other three coding metasurfaces is designed to carry a vortex beam with different topological charges under orthogonal linearly polarized waves with a central frequency of 24 GHz. The experimental results show that the theoretical design is highly consistent with the simulation results. Therefore, it is verified that our proposed 4-bit dual-polarization coding metasurface has a strong and flexible ability to manipulate the beam reflection angle and generate a high-performance dual-mode vortex beam antenna. Because of the wide application prospect of vortex beams in the communication field, we have reason to believe that the proposed ultra-thin dual-mode vortex generator will have potential applications in wireless communication systems in the fields of images and microwaves.
-
Keywords:
- dual-polarization /
- vortex beam /
- coding metasurface
[1] Allen L, Beijersbergen M W, Spreeuw R J, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] Thidé B, Then H, Sjoholm J, Palmer K, Bergman J, Carozzi T, Istomin Y N, Ibragimov N, Khamitova R 2007 Phys. Rev. Lett. 99 087701
Google Scholar
[3] Tamburini F, Mari E, Thide B, Barbieri C, Romanato F 2011 Appl. Phys. Lett. 99 204102
Google Scholar
[4] Babiker M, Power W L, Allen L 1994 Phys. Rev. Lett. 73 1239
Google Scholar
[5] Tennant A, Allen B 2012 Electron. Lett. 48 1365
Google Scholar
[6] Fahrbach F O, Simon P, Rohrbach A 2010 Nat. Photonics 4 780
Google Scholar
[7] Yao A M, Padgett M J 2011 Adv. Opt. Photonics 3 161
Google Scholar
[8] Duocastella M, Arnold C B 2012 Laser Photonics Rev. 6 607
Google Scholar
[9] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313
Google Scholar
[10] Tamburini F, Thidé B, Mari E, Sponselli A, Bianchini A, Romanato F 2012 New J. Phys. 14 118002
Google Scholar
[11] Tamburini F, Mari E, Sponselli A, Thide B, Bianchini A, Romanato F 2012 New J. Phys. 14 033001
Google Scholar
[12] Genevet P, Lin J, Kats M A, Capasso F 2012 Nat. Commun. 3 1278
Google Scholar
[13] Mohammadi S M, Daldorff L K S, Bergman J E S, Karlsson R L, Thidé B, Forozesh K, Carozzi T D, Isham B 2010 IEEE Trans. Antenn. Propag. 58 565
Google Scholar
[14] Meng X S, Wu J J, Wu Z S, Qu T, Yang L 2018 Opt. Express 26 23185
Google Scholar
[15] Meng X S 2019 Appl. Phys. Lett. 114 093504
Google Scholar
[16] Yu S X, Li L, Shi G M, Zhu C, Shi Y 2016 Appl. Phys. Lett. 108 241901
Google Scholar
[17] Kildishev A V, Boltasseva A, Shalaev V M 2013 Science. 339 1232009
Google Scholar
[18] Wakatsuchi H, Kim S, Rushton J J, Sievenpiper D F 2013 Phys. Rev. Lett. 111 245501
Google Scholar
[19] Achouri K, Lavigne G, Caloz C 2016 J. Appl. Phys. 120 235305
Google Scholar
[20] Chen M L N, Li J J, Sha W E I 2017 IEEE Trans. Antenn. Propag. 65 396
Google Scholar
[21] Luo W J, Sun S L, Xu H X, He Q, Zhou L 2017 Phys. Rev. Appl. 7 044033
Google Scholar
-
图 1 (a) 反射型超表面等效电路模型; (b) 亚波长结构及等效电路模型
Fig. 1. Schematic of the equivalent circuit for (a) reflective metasurface and (b) subwavelength structure.
图 2 (a)单元结构的顶部视图; (b)单元结构的侧视图; (c)单元“1/0”在不同极化下的反射相位和幅度
Fig. 2. (a) Top view of unit structure; (b) side view of unit structure; (c) reflection phase and amplitude of unit “1/0” under different polarizations.
图 3 由16个基本单元结构组成的2-bit双极化编码超表面
Fig. 3. The structure consists of 16 basic units composed of 2-bit dual-polarization coding metasurface.
图 4 由256个基本单元结构组成的4-bit双极化编码超表面
Fig. 4. The structure consists of 256 basic units composed of 4-bit dual-polarization coding metasurface.
图 5 由16个各向同性单元结构尺寸组成的4-bit离散反射相位曲线
Fig. 5. A 4-bit discrete reflection phase curve composed of 16 isotropic unit structures of various sizes.
图 6 (a), (b) 携带拓扑荷L为2, 利用1-bit和4-bit构造的离散编码相位分布; (c), (d) 拓扑荷L为2的二维涡旋散射曲线图, 及其近场对应的幅值和相位; (e) 不同bit构造的2阶OAM谱分布对比图
Fig. 6. (a), (b) Discrete encoded phase distributions with topological charge L=2, constructed using 1-bit and 4-bit encoding schemes, respectively; (c), (d) two-dimensional far-field scattering patterns of the L=2 vortex beams; (e) comparison of 2nd-order orbital angular momentum spectra constructed using different bit encoding.
图 7 (a), (c), (e) x极化入射时携带拓扑荷为1, 3, 5的离散编码相位分布; (b), (d), (f) y极化入射时携带拓扑荷为2, 4, 6的离散编码相位分布; (g), (i), (k) x极化入射时携带拓扑荷为1, 3, 5的涡旋电场强度辐射图; (h), (j), (l) y极化入射时携带拓扑荷为2, 4, 6的涡旋电场强度辐射图; (m), (o), (q) x极化入射时携带拓扑荷为1, 3, 5的涡旋电场相位分布图; (n), (p), (r) y极化入射时携带拓扑荷为2, 4, 6的涡旋电场相位分布图
Fig. 7. (a), (c), (e) Phase distributions of discrete coding with topological charges of 1, 3 and 5 under x-polarization incidence; (b), (d), (f) phase distributions of discrete coding with topological charges of 2, 4 and 6 under y-polarization incidence; (g), (i), (k) radiation patterns of vortex electric field intensity with topological charges of 1, 3 and 5 under x-polarization incidence; (h), (j), (l) radiation patterns of vortex electric field intensity with topological charges of 2, 4 and 6 under y-polarization incidence; (m), (o), (q) phase distribution patterns of the vortex electric field with topological charges 1, 3 and 5 under x-polarization incidence; (n), (p), (r) phase distribution patterns of the vortex electric field with topological charges 2, 4 and 6 under y-polarization incidence.
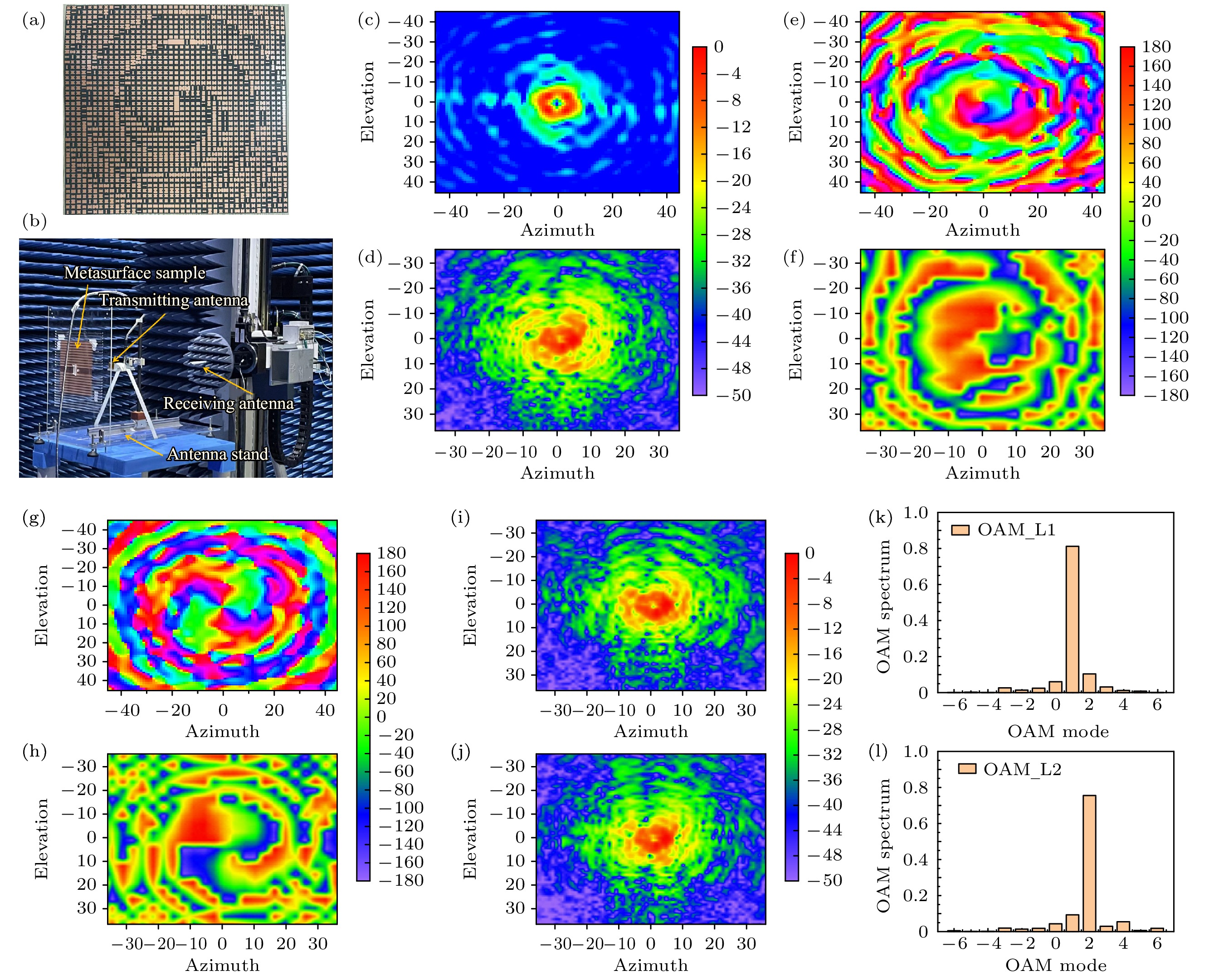
图 8 (a) 双模式涡旋器件的实物拍摄图, 且分别携带拓扑荷1阶和2阶; (b) 实际的测试环境; (c), (d) y极化入射, 在24 GHz时携带拓扑荷为2的仿真和实测涡旋电场强度辐射图; (e)(f) x极化入射, 在24 GHz时携带拓扑荷为1的仿真和实测涡旋电场相位分布图; (g), (h) y极化入射, 在24 GHz时携带拓扑荷为2的仿真和实测涡旋电场相位分布图; (i), (j) y极化入射, 在23 GHz, 25 GHz时携带拓扑荷为2的实测涡旋电场强度辐射图; (k), (l)样品M1在x和y极化下实际测试的OAM谱纯度
Fig. 8. (a) Photography of fabricated sample; (b) the real measurement environment; (c), (d) simulated and measured radiation patterns of vortex electric field intensity at 24 GHz with topological charges of 2 under y-polarization incidence; (e), (f) simulated and measured phase distribution patterns of vortex electric field at 24 GHz with topological charges of 1 under x-polarization incidence; (g), (h) simulated and measured phase distribution patterns of vortex electric field at 24 GHz with topological charges of 2 under y-polarization incidence; (i), (j) measured radiation patterns of vortex electric field intensity at 23 and 25 GHz with topological charges of 2 under y-polarization incidence; (k), (l) actual OAM purity measurements of sample M1 under x and y polarizations, respectively.
表 1 2-bit双极化编码超表面单元结构的几何参数, 符号“/”后的数字代表不同的数字态
Table 1. Geometric parameters of 2-bit dual-polarization coding metasurface unit structure, where the number following the symbol “/” represents different digital states.
参数 a/00 w1/10 w2/10 h1/10 h2/10 a/11 w1/20 w2/20 h1/20 h2/20 a/22 w1/30 w2/30 h1/30 h2/30 值/mm 5 1 4.95 3.61 2.5 3.39 1 4.95 3.39 2.5 3.23 1 4.95 3.11 2.5 参数 a/33 w1/21 w2/21 h1/21 h2/21 w1/31 w2/31 h1/31 h2/31 w1/32 w2/32 h1/32 h2/32 值/mm 3.05 1.2 3.29 3.6 2.8 1.2 3.43 3.3 2.8 1.35 3.1 3.45 2.6 
下载: 导出CSV
-
[1] Allen L, Beijersbergen M W, Spreeuw R J, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] Thidé B, Then H, Sjoholm J, Palmer K, Bergman J, Carozzi T, Istomin Y N, Ibragimov N, Khamitova R 2007 Phys. Rev. Lett. 99 087701
Google Scholar
[3] Tamburini F, Mari E, Thide B, Barbieri C, Romanato F 2011 Appl. Phys. Lett. 99 204102
Google Scholar
[4] Babiker M, Power W L, Allen L 1994 Phys. Rev. Lett. 73 1239
Google Scholar
[5] Tennant A, Allen B 2012 Electron. Lett. 48 1365
Google Scholar
[6] Fahrbach F O, Simon P, Rohrbach A 2010 Nat. Photonics 4 780
Google Scholar
[7] Yao A M, Padgett M J 2011 Adv. Opt. Photonics 3 161
Google Scholar
[8] Duocastella M, Arnold C B 2012 Laser Photonics Rev. 6 607
Google Scholar
[9] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313
Google Scholar
[10] Tamburini F, Thidé B, Mari E, Sponselli A, Bianchini A, Romanato F 2012 New J. Phys. 14 118002
Google Scholar
[11] Tamburini F, Mari E, Sponselli A, Thide B, Bianchini A, Romanato F 2012 New J. Phys. 14 033001
Google Scholar
[12] Genevet P, Lin J, Kats M A, Capasso F 2012 Nat. Commun. 3 1278
Google Scholar
[13] Mohammadi S M, Daldorff L K S, Bergman J E S, Karlsson R L, Thidé B, Forozesh K, Carozzi T D, Isham B 2010 IEEE Trans. Antenn. Propag. 58 565
Google Scholar
[14] Meng X S, Wu J J, Wu Z S, Qu T, Yang L 2018 Opt. Express 26 23185
Google Scholar
[15] Meng X S 2019 Appl. Phys. Lett. 114 093504
Google Scholar
[16] Yu S X, Li L, Shi G M, Zhu C, Shi Y 2016 Appl. Phys. Lett. 108 241901
Google Scholar
[17] Kildishev A V, Boltasseva A, Shalaev V M 2013 Science. 339 1232009
Google Scholar
[18] Wakatsuchi H, Kim S, Rushton J J, Sievenpiper D F 2013 Phys. Rev. Lett. 111 245501
Google Scholar
[19] Achouri K, Lavigne G, Caloz C 2016 J. Appl. Phys. 120 235305
Google Scholar
[20] Chen M L N, Li J J, Sha W E I 2017 IEEE Trans. Antenn. Propag. 65 396
Google Scholar
[21] Luo W J, Sun S L, Xu H X, He Q, Zhou L 2017 Phys. Rev. Appl. 7 044033
Google Scholar
下载:
计量
- 文章访问数: 2639
- PDF下载量: 79
- 被引次数: 0
