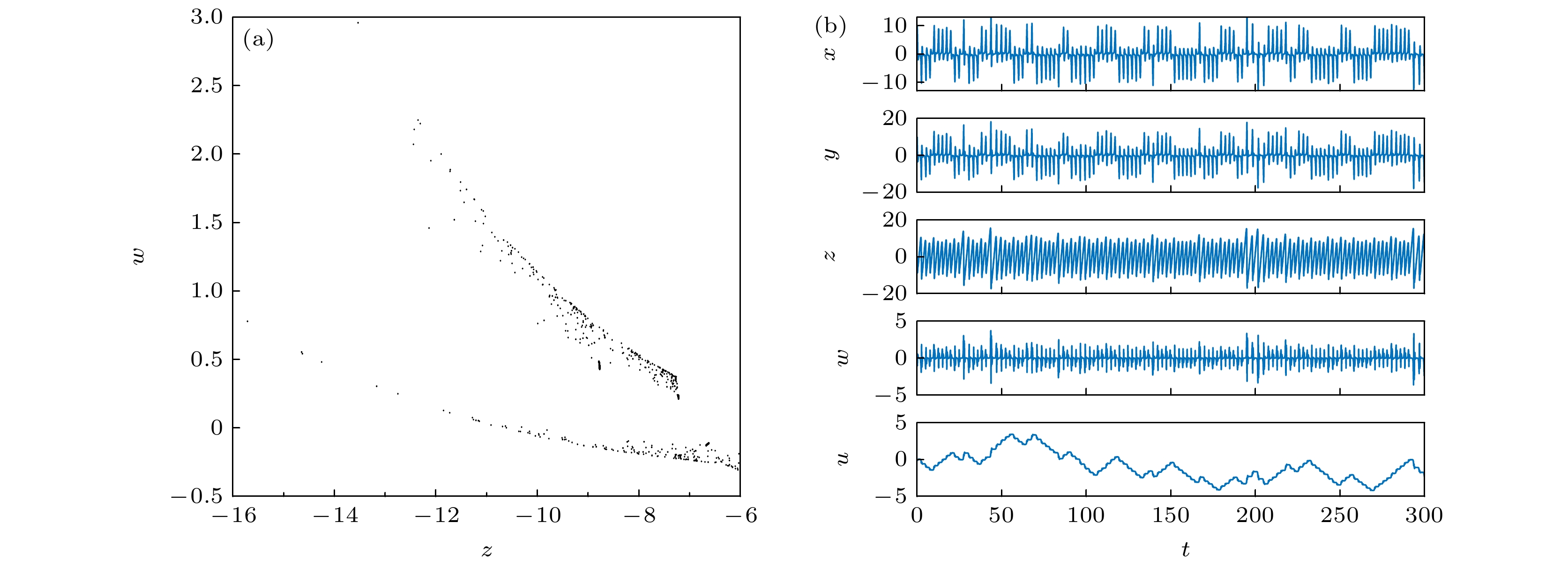
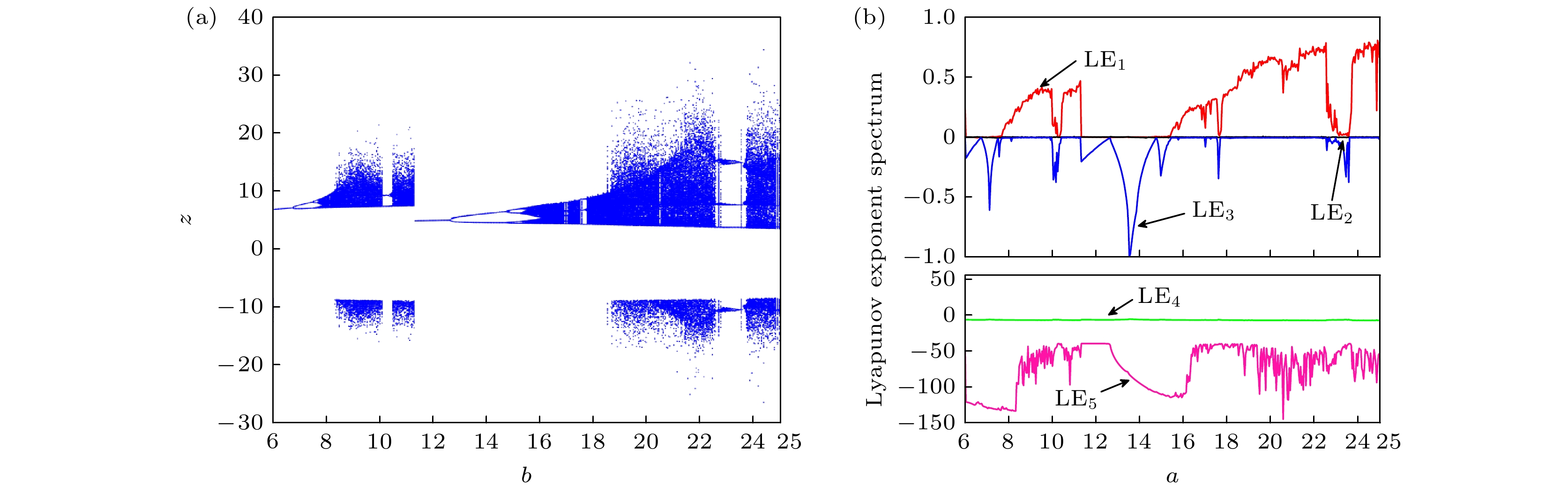
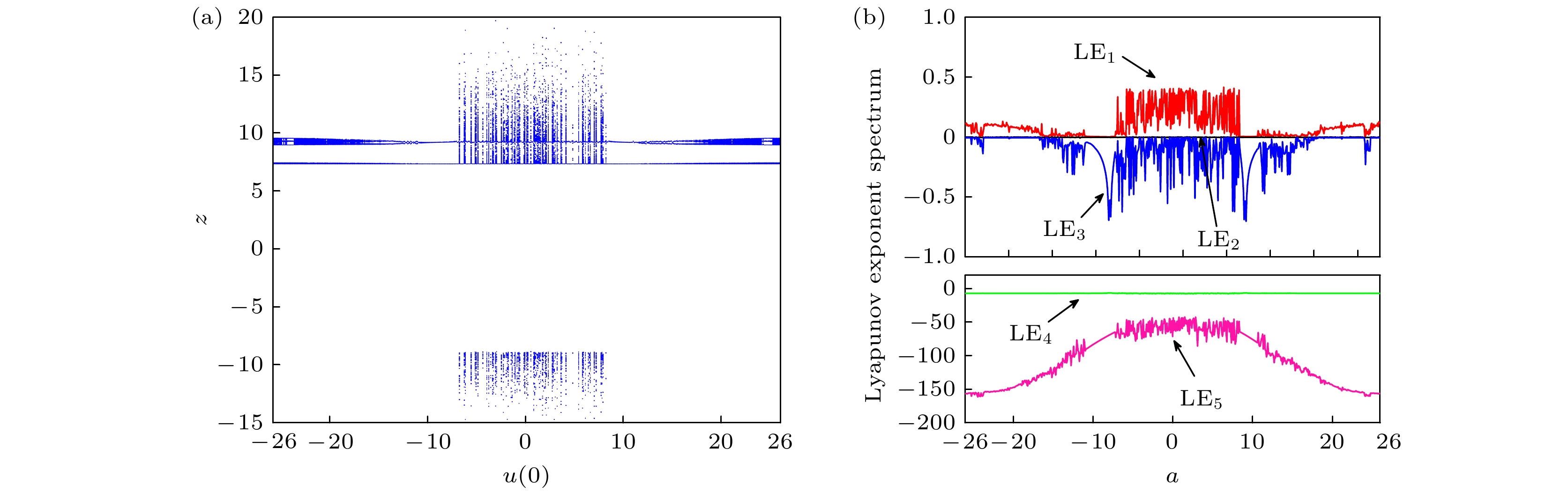
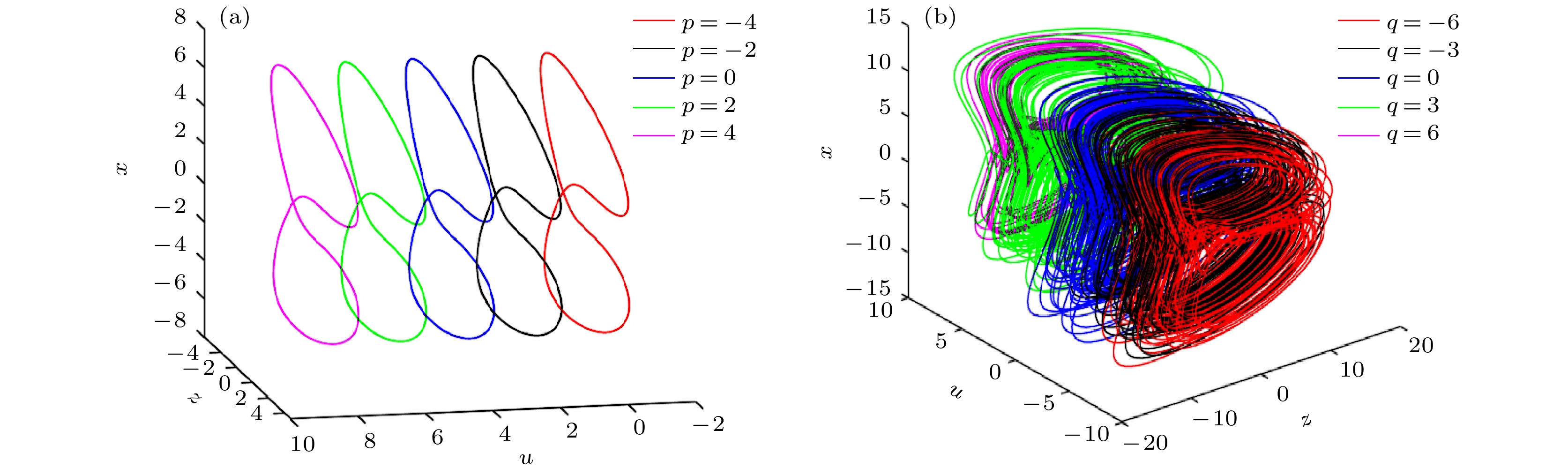
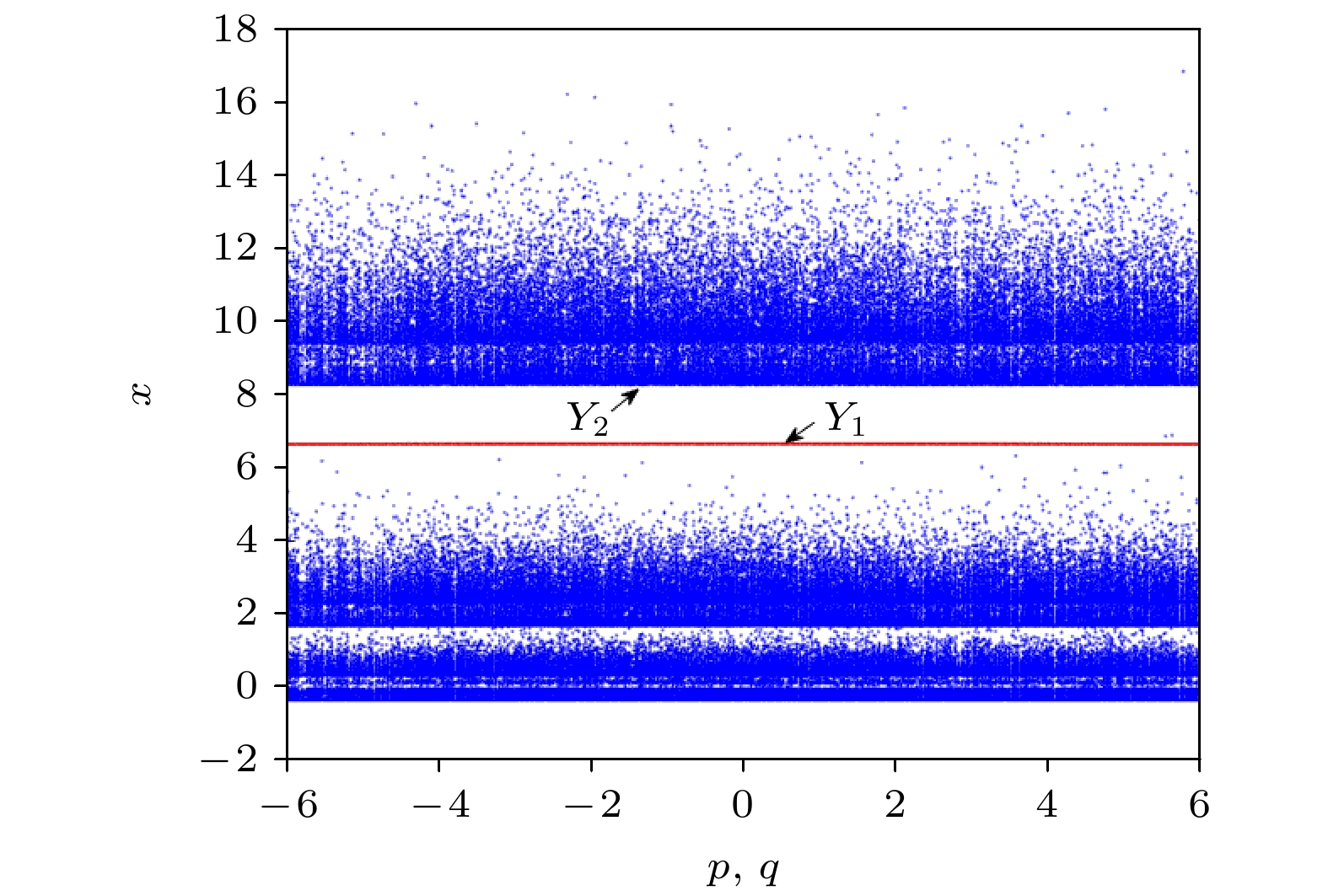
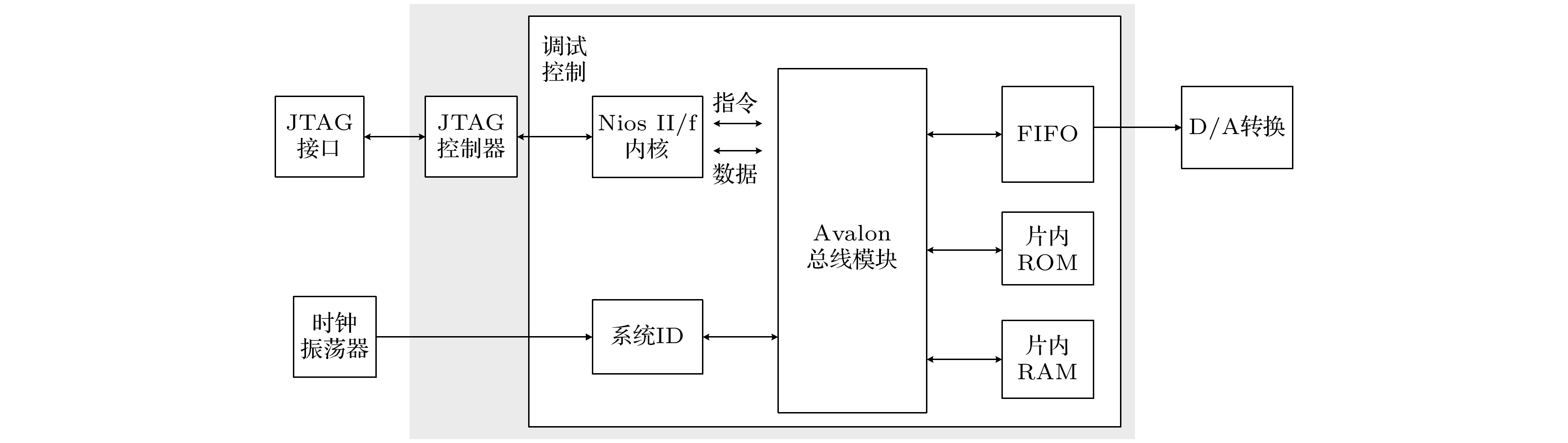
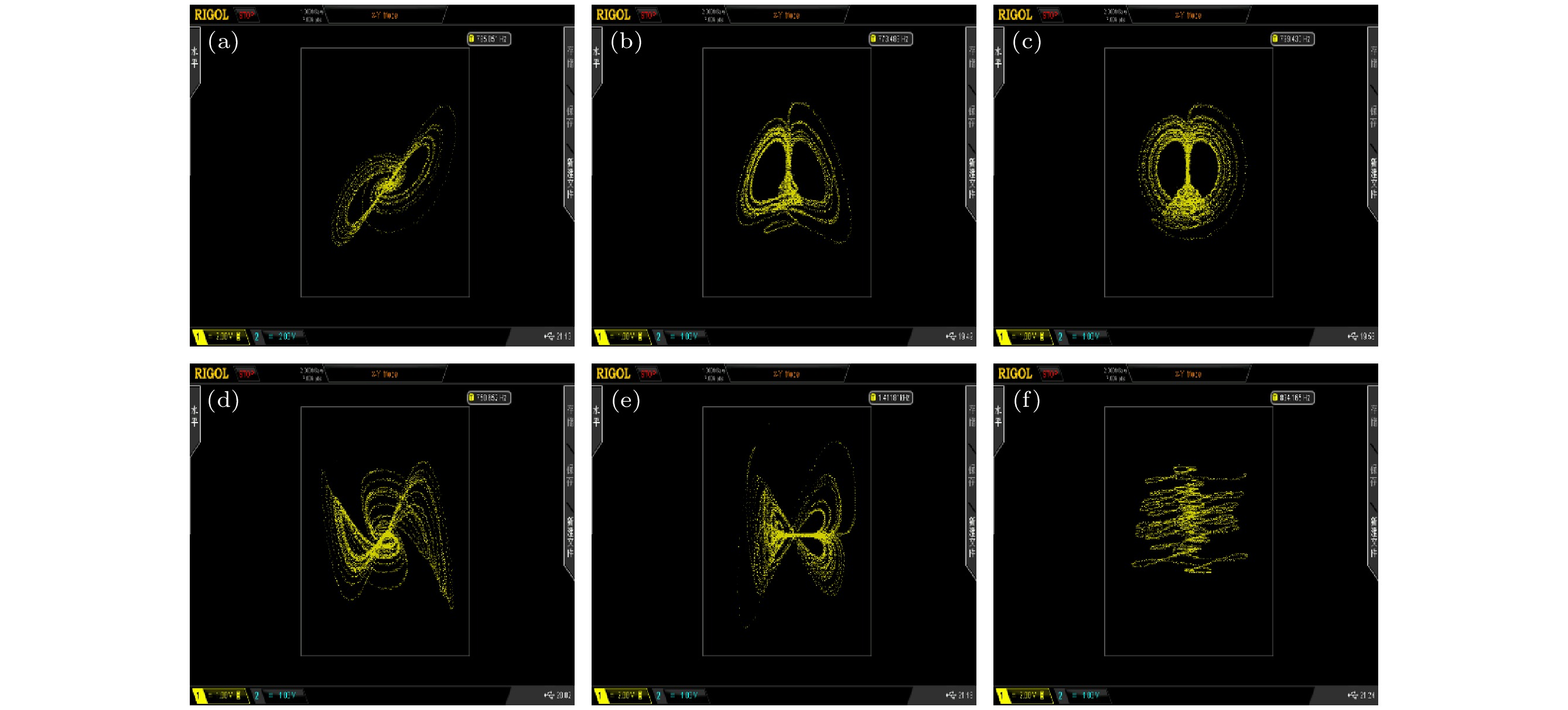
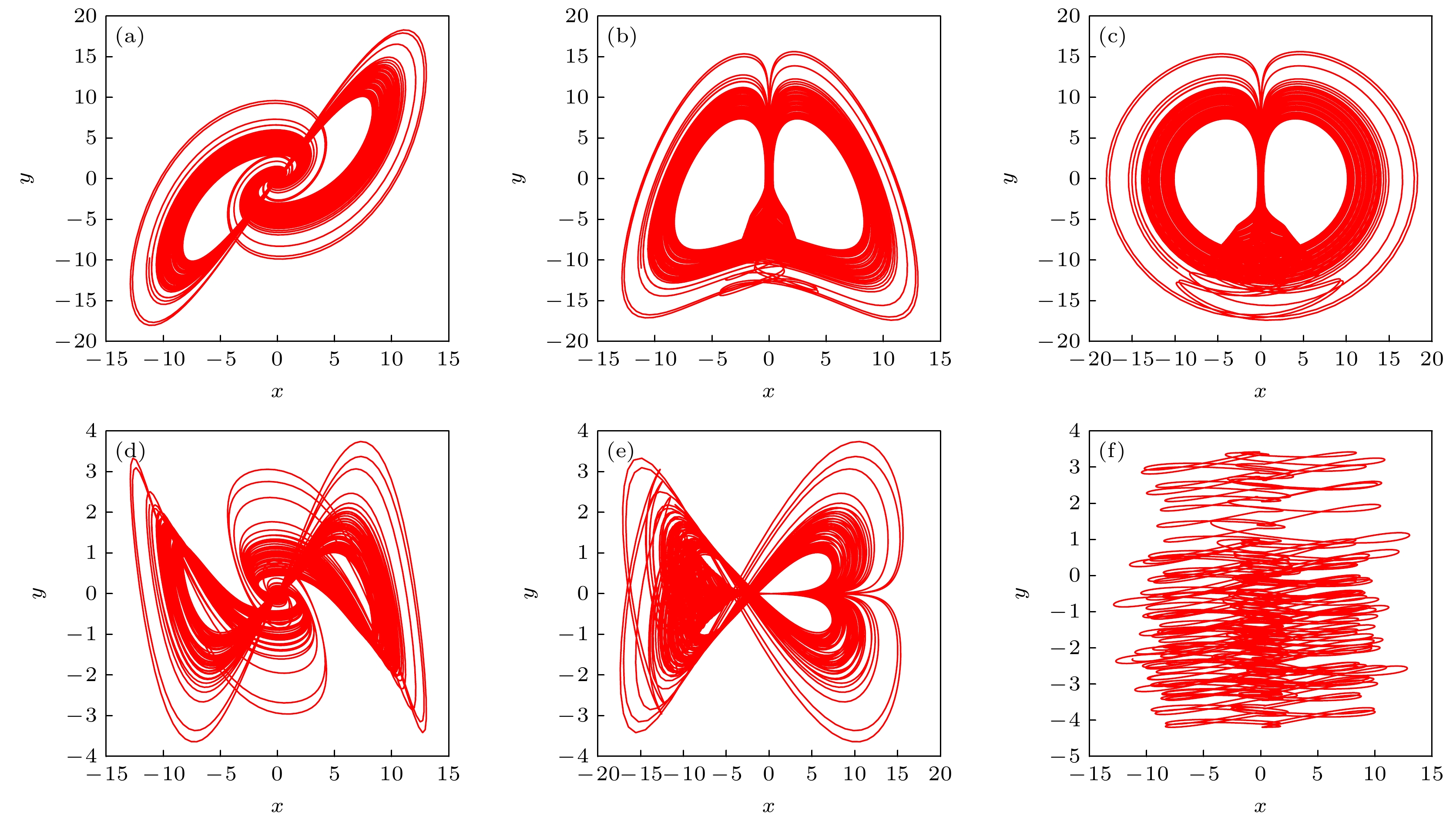
-
The memristor is a kind of nonlinear element with nanometer size, which can enhance the complexity of a chaotic system. With the further research of chaos, several novel nonlinear phenomena have been found by scholars, such as hidden attractors, coexisting attractors and multi-stability. Meanwhile, the extremely multi-stability representation system coexists with the infinite attractors, which has become a hot spot in the field of memristor chaos research in recent years. A general method to construct a chaotic systems of multiple coexistence is to increase the number of equilibrium points of chaotic system by means of control. The introduction of memristor results in the linear distribution of the equilibrium points of chaotic system in space, which are the linear equilibrium points. The existing researches show that chaotic system with extremely multi-stability can produce better chaotic sequence, which can be used in engineering fields such as secure communication. Therefore, it is of great significance to construct chaotic systems with rich dynamic behaviors by using memristors. In order to further improve the complexity of the chaotic system, a five-dimensional memristor chaotic system is constructed by replacing the coupling parameters in the four-dimensional chaotic system based on Sprott-B with a magnetically controlled memristor. The dynamic behavior of the system is analyzed by bifurcation diagram, Lyapunov exponent spectrum, phase portrait, Poincaré map, dynamic map and other conventional means. The analysis shows that the new system has rich dynamic behaviors: when the system parameters change, the system can produce a large number of chaotic attractors with different topological structures and periodic limit cycles with different periods. When different parameters change, the dynamic characteristics of the system also change; when the system parameters are fixed, the system not only has an offset enhancement phenomenon that depends on the change of the initial conditions, but also shows a very strong sensitivity to the initial values and a great adjustment range of the initial values, which leads the infinite chaos and periodic attractors to coexist, namely extremely multi-stability appears. Finally, the digital circuit of the memristor chaotic system is implemented based on the field programmable gate array (FPGA) technology. The phase portrait captured on the oscilloscope is consistent with that from the numerical simulation, which verifies the correctness and realizability of the memristor system. -
Keywords:
- coexisting attractor /
- extremely multistability /
- field programmable gate array /
- memristive chaotic system
[1] Chua L O 1971 IEEE Trans. Circuits Theor. 18 507
Google Scholar
[2] Wen S P, Zeng Z G, Huang T W 2012 Phys. Lett. A 376 2775
Google Scholar
[3] Yang F F, Mou J, Sun K H, Cao Y H, Jin J Y 2019 IEEE Access 7 58751
Google Scholar
[4] 刘嵩, 韦亚萍, 刘静漪, 张国平 2020 华中师范大学学报(自然科学版) 54 36
Google Scholar
Liu S, Wei Y P, Liu J Y, Zhang G P 2020 J. Cent. Chin. Normal Univ. (Nat. Sci.) 54 36
Google Scholar
[5] Zhao L, Hong Q H, Wang X P 2018 Neurocomputing 314 207
Google Scholar
[6] Xu Q, Song Z, Bao H, Chen M, Bao B C 2018 Int. J. Electron. Commun. 96 66
Google Scholar
[7] Hong Q H, Zhao L, Wang X P 2019 Neurocomputing 330 11
Google Scholar
[8] Shin S, Kim K, Kang S M 2012 Electron. Lett. 48 78
Google Scholar
[9] Banerjee S, Parui S, Gupta A 2004 IEEE Trans. Circuits Syst. Ⅱ 51 649
Google Scholar
[10] Min X T, Wang X Y, Zhou P F, Yu S M, Lu H H 2019 IEEE Access 7 124641
Google Scholar
[11] Jin P P, Wang G Y, Lu H H, Fernando T 2017 IEEE Trans. Circuits Syst. Ⅱ 65 246
Google Scholar
[12] 洪庆辉, 曾以成, 李志军 2013 62 230502
Google Scholar
Hong Q H, Zeng Y C, Li Z J 2013 Acta Phys. Sin. 62 230502
Google Scholar
[13] Feudel U 2008 Int. J. Bifurcation Chaos 18 1607
Google Scholar
[14] Bao B C, Bao H, Wang N, Chen M, Xu Q 2017 Chaos, Solitons Fractals 94 102
Google Scholar
[15] Xu Q, Lin Y, Bao B C, Chen M 2016 Chaos, Solitons Fractals 83 186
Google Scholar
[16] Bao B C, Jiang T, Xu Q, Chen M, Wu H G, Hu Y H 2016 Nonlinear Dyn. 86 1711
Google Scholar
[17] Bao B C, Jiang T, Wang G Y, Jin P P, Bao H, Chen M 2017 Nonlinear Dyn. 89 1157
Google Scholar
[18] 闵富红, 王珠林, 曹戈, 王恩荣 2018 电子学报 46 486
Google Scholar
Min F H, Wang Z L, Cao G, Wang E R 2018 Acta Electron. Sin. 46 486
Google Scholar
[19] 秦铭宏, 赖强, 吴永红 2022 71 160502
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
Google Scholar
[20] Lai Q, Kuate P, Pei H, Fostin H 2020 Complexity 86 1711
Google Scholar
[21] Lai Q 2021 Int. J. Bifurcation Chaos 31 2150013
Google Scholar
[22] Li Q D, Zeng H Z, Yang X S 2014 Nonlinear Dyn. 77 255
Google Scholar
[23] 徐强, 杨晓云, 罗姣燕, 徐权 2019 华中师范大学学报(自然科学版) 53 38
Google Scholar
Xu Q, Yang X Y, Luo J Y, Xu Q 2019 J. Cent. Chin. Normal Univ. (Nat. Sci. ) 53 38
Google Scholar
[24] Huang L L, Yao W J, Xiang J H, Zhang Z F 2020 Complexity 2020 1
Google Scholar
[25] 包伯成, 胡文, 许建平, 刘中, 邹凌 2011 60 120502
Google Scholar
Bao B C, Hu W, Xu J P, Liu Z, Zou L 2011 Acta Phys. Sin. 60 120502
Google Scholar
[26] Huang L L, Zhang Z F, Xiang J H, Wang S M 2019 Complexity 2019 1
Google Scholar
[27] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Physica D 16 285
Google Scholar
-
图 1 混沌吸引子相图 (a) x-y平面; (b) x-z平面; (c) y-z平面; (d) x-w平面; (e) z-w平面; (f) x-u平面
Figure 1. Phase portraits of chaotic attractor: (a) x-y plane; (b) x-z plane; (c) y-z plane; (d) x-w plane; (e) z-w plane; (f) x-u plane.
图 2 混沌系统的庞加莱映射和时域波形 (a) 在
$ x = y $ 截面上的庞加莱映射; (b)时域波形Figure 2. Poincaré map and the time domain waveform of the chaotic system: (a) Poincaré map on
$ x = y $ plane; (b) the time domain waveform.
图 3 随系统参数
$ a $ 变化的分岔图和李雅普诺夫指数谱 (a) 分岔图; (b) 李雅普诺夫指数谱Figure 3. Bifurcation diagram and Lyapunov exponent spectrum with
$ a $ : (a) Bifurcation diagram; (b) Lyapunov exponent spectra.
图 5 随系统参数
$ b $ 变化的分岔图和李雅普诺夫指数谱 (a) 分岔图; (b) 李雅普诺夫指数谱Figure 5. Bifurcation diagram and Lyapunov exponent spectrum with
$ b $ : (a) Bifurcation diagram; (b) Lyapunov exponent spectra.
图 6 关于参数
$ b $ 和$ a $ 的动力学地图Figure 6. Dynamical map with respect to parameters
$ b $ and$ a $ 
图 7 当
$ u(0) \in [ - 26, 26] $ 变化时的分岔图和李雅普诺夫指数谱 (a) 分岔图; (b) 李雅普诺夫指数谱Figure 7. Bifurcation diagram and Lyapunov exponent spectrum with
$ u(0) \in [ - 26, 26] $ : (a) Bifurcation diagram; (b) Lyapunov exponent spectra.
图 8 当
$ u(0) \in [10,26] $ 时的分岔图和共存吸引子在三维空间z-u-x的相图 (a) 分岔图; (b) 共存吸引子相图Figure 8. Bifurcation diagram with
$ u(0) \in [10,26] $ and phase portraits of coexisting attractors in three dimensional z-u-x space: (a) Bifurcation diagram; (b) phase portraits of coexisting attractors.
图 9 当
$ x(0) \in [ - 45, 45] $ 时的分岔图和共存吸引子在三维空间z-u-x的相图 (a) 分岔图; (b) 共存吸引子相图Figure 9. Bifurcation diagram with
$ x(0) \in [ - 45, 45] $ and phase portraits of coexisting attractors in three dimensional z-u-x space: (a) Bifurcation diagram; (b) phase portraits of coexisting attractors.
图 10 不同忆阻初始值下的多共存吸引子在三维空间z-u-x的相图 (a) 共存周期吸引子; (b) 共存混沌吸引子
Figure 10. Phase portraits of coexisting many attractors in z-u-x space: (a) Coexisting periodic attractors; (b) coexisting chaotic attractors.
图 11 当
$ p, {\text{ }}q \in [ - 6, 6] $ 时$ {Y_1} $ 和$ {Y_2} $ 的分岔图Figure 11. Bifurcation diagram of
$ {Y_1} $ and$ {Y_{\text{2}}} $ with$p, {\text{ }}q \in $ $ [ - 6, 6]$ .
图 12 系统硬件框图
Figure 12. Hardware structure chart of the system.
图 13 FPGA电路实验结果 (a) x-y平面; (b) x-z平面; (c) y-z平面; (d) x-w平面; (e) z-w平面; (f) x-u平面
Figure 13. Circuit experiment results on FPGA: (a) x-y plane; (b) x-z plane; (c) y-z plane; (d) x-w plane; (e) z-w plane; (f) x-u plane.
表 1 不同系统参数
$ a $ 值对应的吸引子类别及编号Table 1. Attractor types and number corresponding to different values of system with parameter
$ a $ .
DownLoad: CSV
-
[1] Chua L O 1971 IEEE Trans. Circuits Theor. 18 507
Google Scholar
[2] Wen S P, Zeng Z G, Huang T W 2012 Phys. Lett. A 376 2775
Google Scholar
[3] Yang F F, Mou J, Sun K H, Cao Y H, Jin J Y 2019 IEEE Access 7 58751
Google Scholar
[4] 刘嵩, 韦亚萍, 刘静漪, 张国平 2020 华中师范大学学报(自然科学版) 54 36
Google Scholar
Liu S, Wei Y P, Liu J Y, Zhang G P 2020 J. Cent. Chin. Normal Univ. (Nat. Sci.) 54 36
Google Scholar
[5] Zhao L, Hong Q H, Wang X P 2018 Neurocomputing 314 207
Google Scholar
[6] Xu Q, Song Z, Bao H, Chen M, Bao B C 2018 Int. J. Electron. Commun. 96 66
Google Scholar
[7] Hong Q H, Zhao L, Wang X P 2019 Neurocomputing 330 11
Google Scholar
[8] Shin S, Kim K, Kang S M 2012 Electron. Lett. 48 78
Google Scholar
[9] Banerjee S, Parui S, Gupta A 2004 IEEE Trans. Circuits Syst. Ⅱ 51 649
Google Scholar
[10] Min X T, Wang X Y, Zhou P F, Yu S M, Lu H H 2019 IEEE Access 7 124641
Google Scholar
[11] Jin P P, Wang G Y, Lu H H, Fernando T 2017 IEEE Trans. Circuits Syst. Ⅱ 65 246
Google Scholar
[12] 洪庆辉, 曾以成, 李志军 2013 62 230502
Google Scholar
Hong Q H, Zeng Y C, Li Z J 2013 Acta Phys. Sin. 62 230502
Google Scholar
[13] Feudel U 2008 Int. J. Bifurcation Chaos 18 1607
Google Scholar
[14] Bao B C, Bao H, Wang N, Chen M, Xu Q 2017 Chaos, Solitons Fractals 94 102
Google Scholar
[15] Xu Q, Lin Y, Bao B C, Chen M 2016 Chaos, Solitons Fractals 83 186
Google Scholar
[16] Bao B C, Jiang T, Xu Q, Chen M, Wu H G, Hu Y H 2016 Nonlinear Dyn. 86 1711
Google Scholar
[17] Bao B C, Jiang T, Wang G Y, Jin P P, Bao H, Chen M 2017 Nonlinear Dyn. 89 1157
Google Scholar
[18] 闵富红, 王珠林, 曹戈, 王恩荣 2018 电子学报 46 486
Google Scholar
Min F H, Wang Z L, Cao G, Wang E R 2018 Acta Electron. Sin. 46 486
Google Scholar
[19] 秦铭宏, 赖强, 吴永红 2022 71 160502
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
Google Scholar
[20] Lai Q, Kuate P, Pei H, Fostin H 2020 Complexity 86 1711
Google Scholar
[21] Lai Q 2021 Int. J. Bifurcation Chaos 31 2150013
Google Scholar
[22] Li Q D, Zeng H Z, Yang X S 2014 Nonlinear Dyn. 77 255
Google Scholar
[23] 徐强, 杨晓云, 罗姣燕, 徐权 2019 华中师范大学学报(自然科学版) 53 38
Google Scholar
Xu Q, Yang X Y, Luo J Y, Xu Q 2019 J. Cent. Chin. Normal Univ. (Nat. Sci. ) 53 38
Google Scholar
[24] Huang L L, Yao W J, Xiang J H, Zhang Z F 2020 Complexity 2020 1
Google Scholar
[25] 包伯成, 胡文, 许建平, 刘中, 邹凌 2011 60 120502
Google Scholar
Bao B C, Hu W, Xu J P, Liu Z, Zou L 2011 Acta Phys. Sin. 60 120502
Google Scholar
[26] Huang L L, Zhang Z F, Xiang J H, Wang S M 2019 Complexity 2019 1
Google Scholar
[27] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Physica D 16 285
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4889
- PDF Downloads: 131
- Cited By: 0
