-
Active polymers exhibit very rich dynamic behaviors due to their deformable long-chain architecture. In this work, we perform Langevin dynamics simulations to study the behavior of a single self-propelled polymer chain in a plane (two dimensions) whose activity can be tuned by external field. We consider a spatially on-off periodic field along the x direction, i.e. the plane is patterned into stripes of alternating active region and passive region. The width d of the stripe (half period length) plays a key role in determining the kinetic behavior of a flexible polymer chain. When
$ d\gg 2{R}_{\rm{g}0} $ ($ {R}_{\rm{g}0} $ is the radius of gyration of the passive flexible chain in the random coil state), the polymer chain can stay for a long time in either the active region or the passive region and moves mainly by slow Brownian diffusion; when$ 2{R}_{\rm{L}} < d < 2{R}_{\rm{g}0} $ ($ {R}_{\rm{L}} $ is the radius of the spiral formed by the self-propelled polymer chain), the polymer chain could stay entirely in one region but cross-regional motion happens frequently; when$ d < 2{R}_{\rm{L}} $ , the polymer chain does not stay entirely in one region but keeps moving cross-regionally accompanied by the stretching of the parts in active regions. With the kinetic behavior of the polymer chain changing as d varies, the long-time diffusive coefficient changes by as great as two orders of magnitude and other statistical quantities such as spatial density distribution, mean total propelling force, characteristic size and orientation all show non-monotonic variations. In addition, we find four typical processes of the cross-regional motion of a flexible chain. For a semiflexible polymer chain, the cross-regional motion is accompanied by buckling behavior and the width d affects greatly the degree of buckling and the continuity of the motion. Our work suggests a new idea for tuning and controlling the dynamic behavior of active polymers and provides a reference for the design and the potential applications of chain-like active materials.-
Keywords:
- active matter /
- active polymer /
- nonequilibrium system /
- dynamics
[1] Schaller V, Weber C, Semmrich C, Frey E, Bausch A R 2010 Nature 467 73
Google Scholar
[2] Sumino Y, Nagai K H, Shitaka Y, Tanaka D, Yoshikawa K, Chate H, Oiwa K 2012 Nature 483 448
Google Scholar
[3] Sohn M H, Seo K W, Choi Y S, Lee S J, Kang Y S, Kang Y S 2010 Marine Biology 158 561
Google Scholar
[4] Elgeti J, Winkler R G, Gompper G 2015 Rep. Prog. Phys. 78 056601
Google Scholar
[5] Yan J, Han M, Zhang J, Xu C, Luijten E, Granick S 2016 Nat. Mater. 15 1095
Google Scholar
[6] Eisenstecken T, Gompper G, Winkler R 2016 Polymers 8 304
Google Scholar
[7] Eisenstecken T, Gompper G, Winkler R G 2017 J. Chem. Phys. 146 154903
Google Scholar
[8] Harder J, Valeriani C, Cacciuto A 2014 Phys. Rev. E 90 062312
Google Scholar
[9] Wang Y K, Lo C J, Lo W C 2018 Phys. Rev. E 98 062613
Google Scholar
[10] Mokhtari Z, Zippelius A 2019 Phys. Rev. Lett. 123 028001
Google Scholar
[11] Pu M, Jiang H, Hou Z 2016 J. Chem. Phys. 145 174902
Google Scholar
[12] Isele-Holder R E, Elgeti J, Gompper G 2015 Soft Matter 11 7181
Google Scholar
[13] Isele-Holder R E, Jager J, Saggiorato G, Elgeti J, Gompper G 2016 Soft Matter 12 8495
Google Scholar
[14] Arlt J, Martinez V A, Dawson A, Pilizota T, Poon W C K 2018 Nat. Commun. 9 768
Google Scholar
[15] Row H, Brady J F 2020 Phys. Rev. E 101 062604
Google Scholar
[16] Caprini L, Marini Bettolo Marconi U, Wittmann R, Lowen H 2022 Soft Matter 18 1412
Google Scholar
[17] Heyes D M, Okumura H 2006 J. Chem. Phys. 124 164507
Google Scholar
[18] Mackay F E, Ollila S, Denniston C 2013 Comput. Phys. Commun. 184 2021
Google Scholar
[19] Victor J M, Lhuillier D 1990 J. Chem. Phys. 92 1362
Google Scholar
[20] Michael R, Ralph H C 2003 Polymer Physics (Oxford: Oxford University Press) p311
-
图 1 空间调制场与活性聚合物示意图(
$ d=32\sigma $ ,${L}_{x}= $ $ 192\sigma$ )Figure 1. Schematic diagram of spatial modulation field and an active polymer (
$ d=32\sigma $ ,$ {L}_{x}=192\sigma $ ).
图 2 活性力示意图
Figure 2. Schematic diagram of active force.
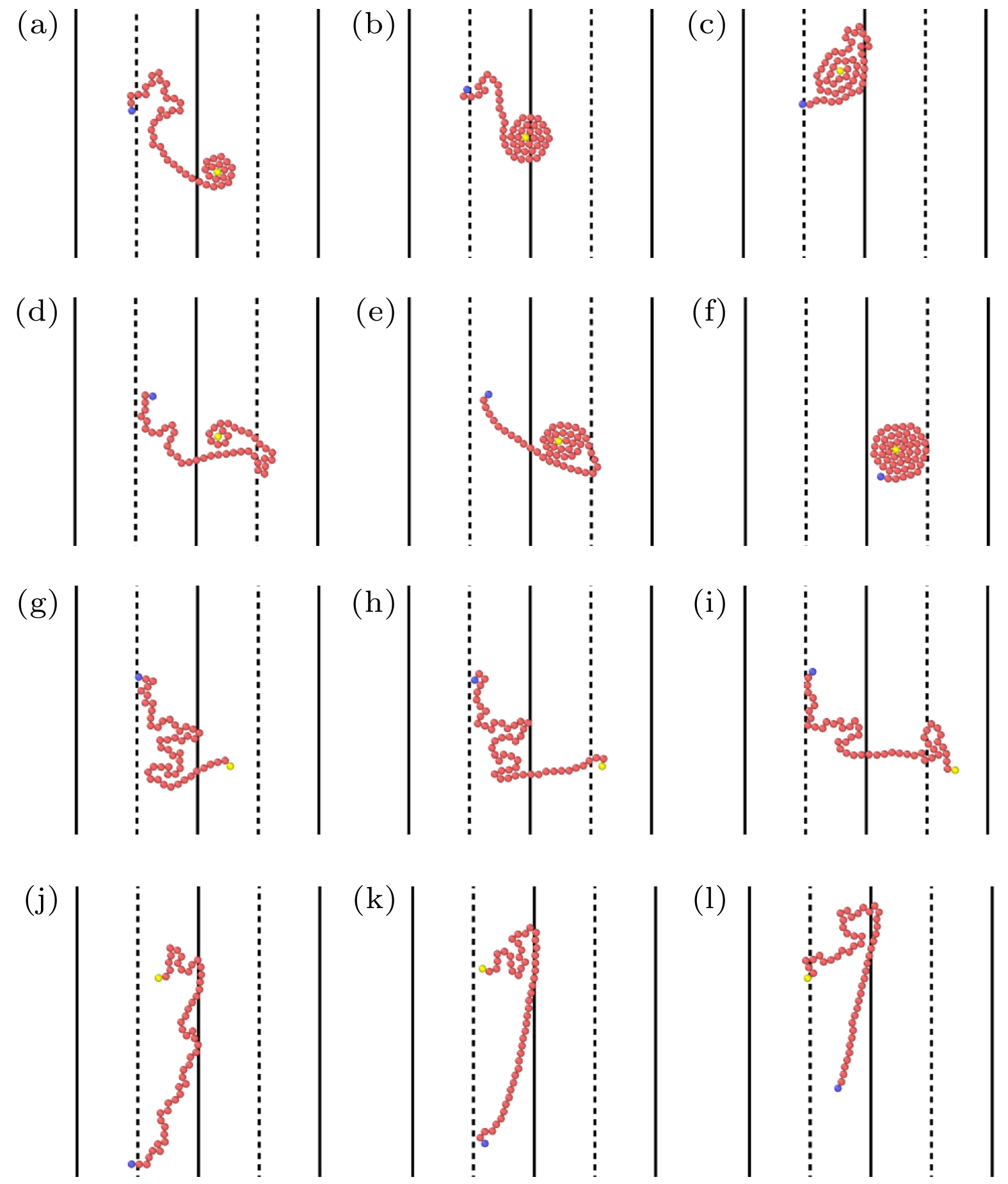
图 3 柔性链在不同区域宽度下的构象快照 (黄色粒子代表聚合物链头部, 蓝色粒子代表聚合物链尾端) (a) d = 32, 活性区域的稳定螺旋态以及非活性区域的无规线团状态; (b)—(f) d = 8, 活性区的螺旋态、非活性区的拉伸的无规线团以及各种跨区域瞬时构象; (g), (h) d = 3, 跨区域的拉伸和卷曲塌缩构象
Figure 3. Snapshots of the conformation of the flexible chain at different region widths (Yellow particles represent the head of polymer chain, while blue particles represent the tail of polymer chain): (a) d = 32, stable helical state in the active region and random coil state in the inactive region; (b)–(f) d = 8, helical state in the active region, stretched random coil state and various cross-regional instantaneous conformations in the inactive region; (g), (h) d = 3, cross-regional stretched and curled collapsed conformations.
图 4 柔性链跨区域运动的快照(
$ d=8 $ ) (a)—(c) 第一种跨区域运动模式, 即头部从非活性区进入活性区, 很快形成螺旋并最终返回非活性区; (d)—(f) 第二种跨区域运动模式, 即头部从非活性区进入活性区, 在大部分链段进入活性区后形成螺旋并最终在活性区形成完整螺旋; (g)—(i) 第三种跨区域运动模式, 即头部从非活性区进入活性区, 并跨越整个活性区进入下一个非活性区; (j)—(l) 第四种跨区域运动模式, 即中间部分从非活性区进入活性区造成其后面的链段产生明显的(沿纵向即y方向的)拉伸Figure 4. Snapshots of cross region motion of the flexible chain (
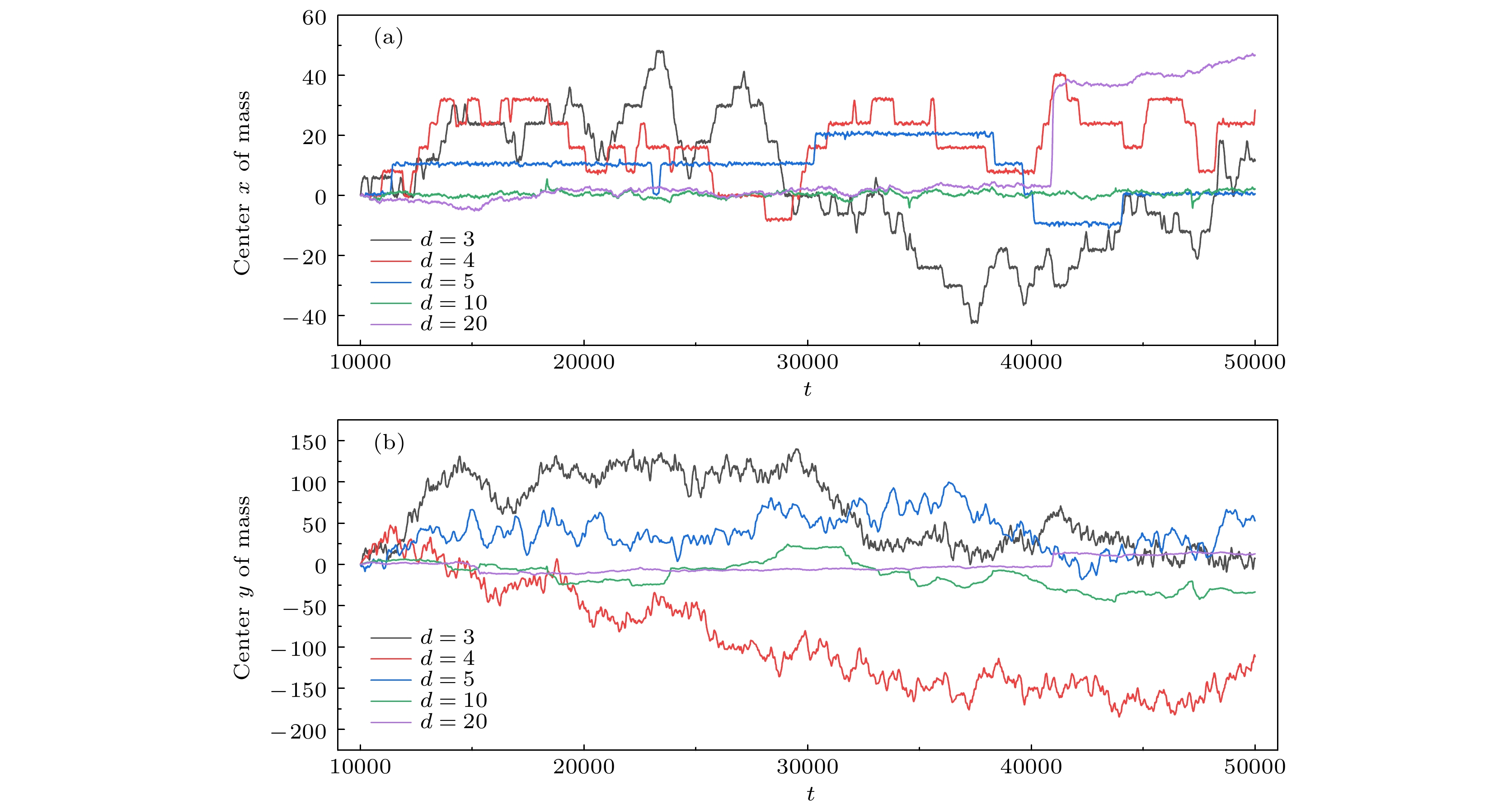
$ d=8 $ ). (a)–(c) The first mode of cross region motion: the head enters active region from the passive region, rapidly forms spiral and eventually returns to the passive region. (d)–(f) The second mode of cross region motion: the head enters active region from the passive region, forms spiral after most of the chain segments have entered active region and eventually forms complete spiral in the active region. (g)–(i) The third cross regional motion mode: the head enters active region from the passive region and crosses the entire active region to the next passive region. (j)–(l) The fourth mode of crosss region motion: the middle segments enter active region from the passive zone causing significant stretch (longitudinal, i.e.$ y $ -direction) of the chain segments behind it.
图 5 不同区域宽度下柔性链的质心均方位移 (不同颜色曲线对应不同区域宽度, 断线表示不同的扩散系数)
Figure 5. Mean square displacement (center-of-mass) of the flexible chain under different regional widths (Different color curves correspond to different regional widths, and the broken line indicates different diffusion coefficients).
图 6 柔性链在不同区域宽度的周期性外场中, 质心沿(a) x方向和(b) y方向随时间运动的位置变化. 在d = 3, 4, 5时, x方向的位置变化出现平台与跳跃, 平台对应链被限制在非活性区域, 跳跃则对应链跨越活性区域; y方向的位置变化出现正常的涨落. 在d = 10, 20时, 链的运动幅度相对较小
Figure 6. In the periodic external field of the flexible chain with different regional widths, the position change of the center of the mass moving along (a) x direction and (b) y direction with time. Different color curves represent different regional widths d respectively. At d = 3, 4, 5, the position changes in the x direction appear platform and jump. The chain corresponding to platform is restricted to the passive region, while the chain corresponding to jump crosses the active region. The change of position in the y direction shows normal fluctuation. At d = 10, 20, the movement of the chain is relatively small.
图 7 柔性链的区域概率分布
$\varphi$ (a)和平均螺旋角$\theta$ (b)与区域宽度d的变化关系Figure 7. Regional probability distribution
$\varphi$ of the flexible chain (a) and the average spiral angle$\theta$ (b) in relation to the variation of the region width d
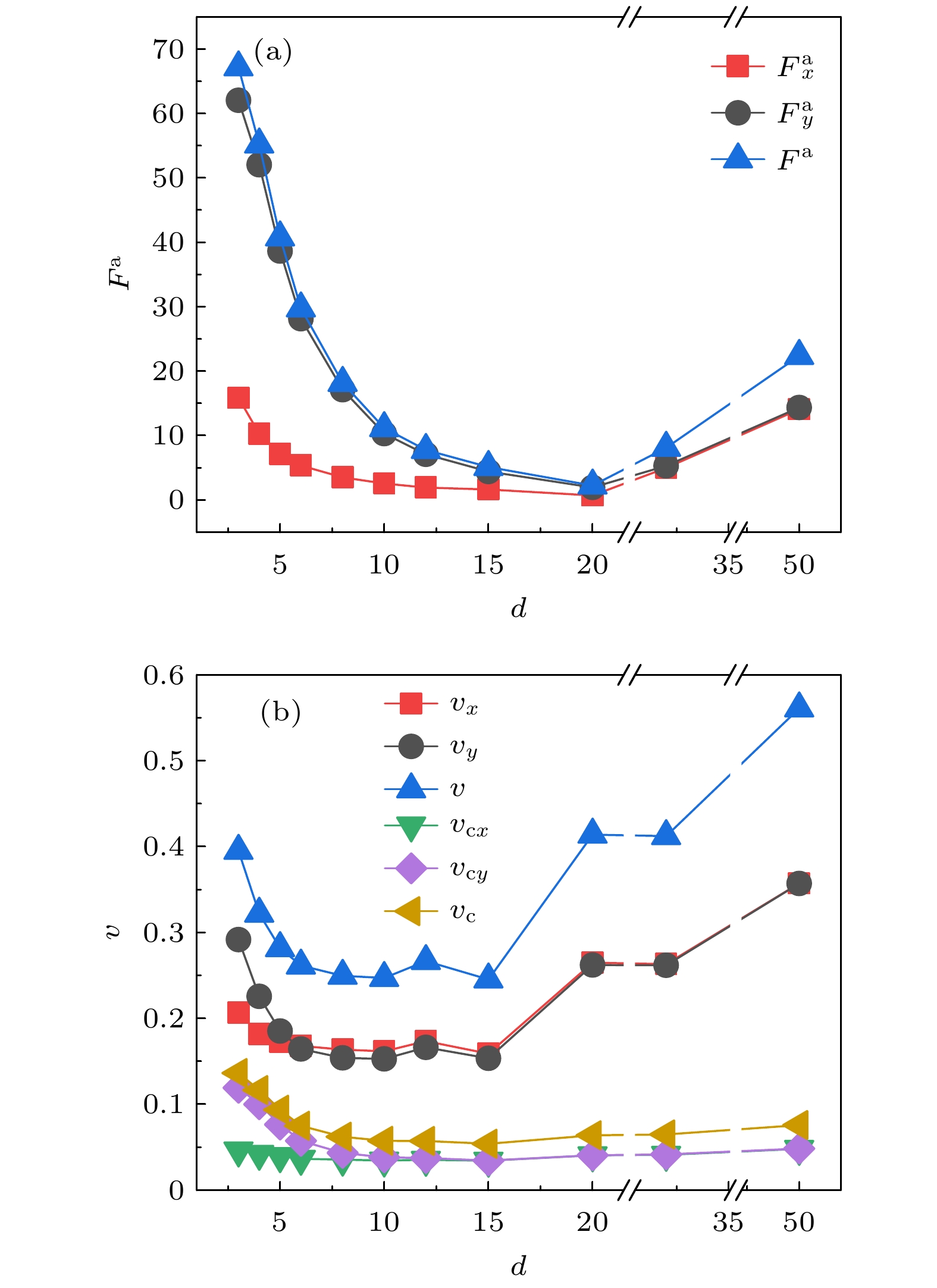
图 8 (a) 柔性链的活性力
$ {F}^{\rm{a}} $ 与区域宽度$ d $ 的非单调变化关系; (b) 柔性链的粒子和质心的短时平均速度($ v $ 和$ {v}_{\rm{c}} $ )与区域宽度$ d $ 的变化关系Figure 8. (a) Nonmonotonic variation relationship between the active force
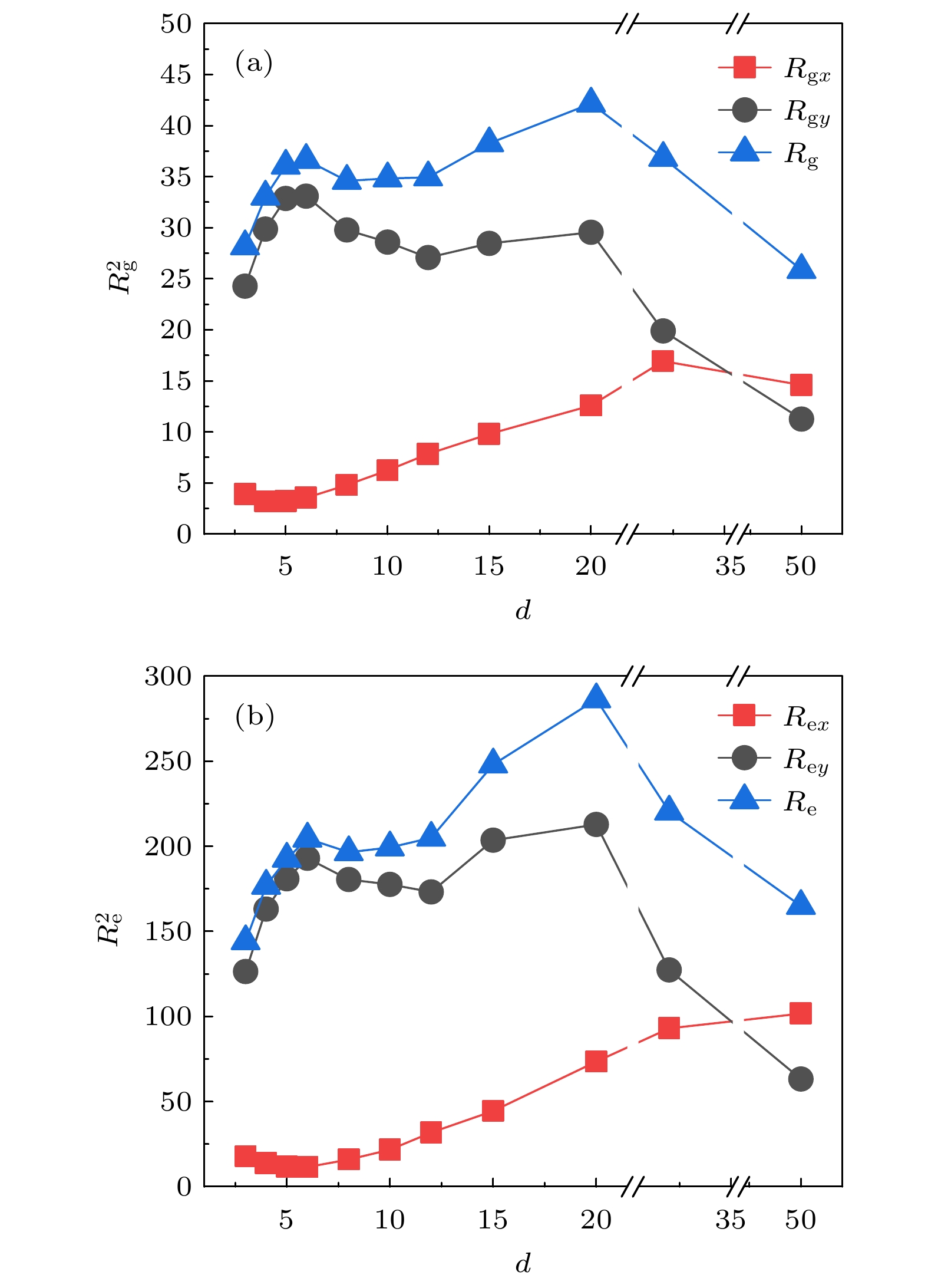
$ {F}^{\rm{a}} $ and the region width$ d $ of the flexible chain; (b) the short-term average velocity of particles and center of mass of the flexible chain ($ v $ and$ {v}_{\rm{c}} $ ) in relation to the variation of the region width d
图 9 柔性链的回转半径
$ {R}_{\rm{g}} $ (a)和均方末端距$ {R}_{\rm{e}} $ (b)与区域宽度d的变化关系, 在d = 6附近$ {R}_{\rm{g}} $ ,$ {R}_{\rm{e}} $ 出现峰值, 两者走势相似Figure 9. Radius of gyration of the flexible chain
$ {R}_{\rm{g}} $ (a) and the mean square end-to-end distance$ {R}_{\rm{e}} $ (b) in relation to the variation of the region width d. Peaks of$ {R}_{\rm{g}} $ and$ {R}_{\rm{e}} $ occur around d = 6, both are similar.
图 10 柔性链的向列序参数
$ S $ 与区域宽度$ d $ 的非单调性变化关系, 在$ d=5 $ 左右存在峰值,$ {S}_{\rm{a}} $ 相对变化较大Figure 10. Nonmonotonic relationship of the nematic order parameter
$ S $ and the region width$ d $ of the flexible chain. There is a peak around d = 5, and the change of$ {S}_{\rm{a}} $ is large relatively.
图 11 半刚性链跨区域运动的快照(
$ d=8 $ ), 头部从非活性区进入活性区失去自驱力, 链段往前推挤形成屈曲拱起Figure 11. Snapshot of the across region motion of the semi-rigid chain (
$ d=8 $ ). The head enters the active region from passive and loses self-propelled force, and the chain segment is pushed forward to form buckling.
图 12 半刚性链在不同区域宽度下的构象快照 (a) d = 8, 非活性区的沿y方向伸展状态; (b), (c) d = 6, 跨区域的屈曲和屈曲折叠构象; (d) d = 3, 跨越多个区域的蛇行构象
Figure 12. Snapshots of the conformation of semi-rigid chains at different domain widths: (a) d = 8, stretching along the y-direction in the inactive region; (b), (c) d = 6, buckling and buckling-folded conformation across regions; (d) d = 3, serpentine conformation spanning multiple regions.
图 13 (a)半刚性链的区域概率分布
$ \phi $ 与区域宽度$ d $ 的单调变化关系; (b)半刚性链的活性力$ {F}^{\rm{a}} $ 与区域宽度$ d $ 的变化关系; (c)半刚性链的粒子和质心的短时平均速度($ v $ 和$ {v}_{\rm{c}} $ )与区域宽度$ d $ 的变化关系Figure 13. (a) Monotonous variation relationship with the regional probability distribution
$ \phi $ and the region width$ d $ of the semi-rigid chain; (b) relationship between the active force$ {F}^{\rm{a}} $ and the variation of the region width d of the semi-rigid chain; (c) the short-term average velocity of particles and center of mass of the semi-rigid chain ($ v $ and$ {v}_{\rm{c}} $ ) in relation to the region width d
图 14 半刚性链的回转半径
$ {R}_{\rm{g}} $ (a)和均方末端距$ {R}_{\rm{e}} $ (b)随区域宽度$ d $ 的变化关系, 在$ d=6 $ 时链的整体尺寸出现最低点; (c)半刚性链的向列序参数随区域宽度$ d $ 的变化关系, 在$ d=6 $ 时,$ {S}_{\rm{a}} $ 出现峰值Figure 14. Radius of gyration of the semi-rigid chain
$ {R}_{\rm{g}} $ (a) and the mean square end-to-end distance$ {R}_{\rm{e}} $ (b) in relation to the variation of the region width d. The overall size of the chain at$ d=6 $ is the lowest point. (c) The relationship between the nematic order parameter of the semi-rigid chain with the width of the region d. At d = 6, the$ {S}_{\rm{a}} $ shows peak. -
[1] Schaller V, Weber C, Semmrich C, Frey E, Bausch A R 2010 Nature 467 73
Google Scholar
[2] Sumino Y, Nagai K H, Shitaka Y, Tanaka D, Yoshikawa K, Chate H, Oiwa K 2012 Nature 483 448
Google Scholar
[3] Sohn M H, Seo K W, Choi Y S, Lee S J, Kang Y S, Kang Y S 2010 Marine Biology 158 561
Google Scholar
[4] Elgeti J, Winkler R G, Gompper G 2015 Rep. Prog. Phys. 78 056601
Google Scholar
[5] Yan J, Han M, Zhang J, Xu C, Luijten E, Granick S 2016 Nat. Mater. 15 1095
Google Scholar
[6] Eisenstecken T, Gompper G, Winkler R 2016 Polymers 8 304
Google Scholar
[7] Eisenstecken T, Gompper G, Winkler R G 2017 J. Chem. Phys. 146 154903
Google Scholar
[8] Harder J, Valeriani C, Cacciuto A 2014 Phys. Rev. E 90 062312
Google Scholar
[9] Wang Y K, Lo C J, Lo W C 2018 Phys. Rev. E 98 062613
Google Scholar
[10] Mokhtari Z, Zippelius A 2019 Phys. Rev. Lett. 123 028001
Google Scholar
[11] Pu M, Jiang H, Hou Z 2016 J. Chem. Phys. 145 174902
Google Scholar
[12] Isele-Holder R E, Elgeti J, Gompper G 2015 Soft Matter 11 7181
Google Scholar
[13] Isele-Holder R E, Jager J, Saggiorato G, Elgeti J, Gompper G 2016 Soft Matter 12 8495
Google Scholar
[14] Arlt J, Martinez V A, Dawson A, Pilizota T, Poon W C K 2018 Nat. Commun. 9 768
Google Scholar
[15] Row H, Brady J F 2020 Phys. Rev. E 101 062604
Google Scholar
[16] Caprini L, Marini Bettolo Marconi U, Wittmann R, Lowen H 2022 Soft Matter 18 1412
Google Scholar
[17] Heyes D M, Okumura H 2006 J. Chem. Phys. 124 164507
Google Scholar
[18] Mackay F E, Ollila S, Denniston C 2013 Comput. Phys. Commun. 184 2021
Google Scholar
[19] Victor J M, Lhuillier D 1990 J. Chem. Phys. 92 1362
Google Scholar
[20] Michael R, Ralph H C 2003 Polymer Physics (Oxford: Oxford University Press) p311
DownLoad:
Catalog
Metrics
- Abstract views: 3457
- PDF Downloads: 71
- Cited By: 0
