-
The lack of the relationship between flux and charge has been made up for by the memristor which is suitable to constructing chaotic circuits as a nonlinear element. Commonly, the memristor-based chaotic systems are constructed by introducing the model of memristor into various classical nonlinear circuits, and more special and abundant dynamic behaviors are existent in these memristive systems. With the deepening of research, several novel nonlinear phenomena of memristor circuits have been found, such as hidden attractors, self-excited attractors and anti-monotonic characteristic. Meanwhile, multistability of a memristor-based circuit explained by the coexistence of multiple attractors with different topological structures is a typical phenomenon in a nonlinear system, and it is also one of the hotspots in this field. In addition, the chaotic sequences generated by the memristive circuits are used as additional signals for information transmission or image encryption. Therefore, the study of modeling memristor systems and analyzing various nonlinear behaviors is of certain valuable. In this paper, a four-dimensional flux-controlled memeristive circuit is constructed by introducing an active memristor with absolute value into an improved Chua’s circuit, and the special dynamic behaviors are observed. Through the bifurcation diagrams and Lyapunov exponent spectra, the symmetric bifurcations are shown, and the symmetric system states in parameter mappings are found. Besides, the distribution maps of memristive circuit are used to analyze the multistability in a symmetrical attraction domain, and the corresponding phase diagrams are depicted to confirm the existence of multistability. Furthermore, the circuit experiments of the flux-controlled memeristive circuit are implemented by the field programmable gate array simulation, and the experimental results are obtained on a digital oscilloscope, which proves the physical implementability of the memristor-based system. -
Keywords:
- flux-controlled memristor circuit /
- symmetrical dynamic behaviors /
- multistability /
- field programmable gate array
[1] Chua L O 1971 IEEE Trans. Circ. Theory 18 507
Google Scholar
[2] 林毅, 刘文波, 沈骞 2018 67 230502
Google Scholar
Lin Y, Liu W B, Shen Q 2018 Acta Phys. Sin. 67 230502
Google Scholar
[3] Olumodeji O A, Gottardi M 2017 Integration 58 438
Google Scholar
[4] Joglekar Y N, Wolf S J 2009 Eur. J. Phys. 30 661
Google Scholar
[5] Guo M, Gao Z H, Xue Y B, Dou G, Li Y X 2018 Nonlinear Dyn. 93 1681
Google Scholar
[6] Wang C H, Liu X M, Xia H 2017 Chaos 27 033114
Google Scholar
[7] Peng G Y, Min F H 2017 Nonlinear Dyn. 90 1607
Google Scholar
[8] Li C, Min F H, Li C B 2018 Nonlinear Dyn. 94 2785
Google Scholar
[9] Peng G, Min F 2018 Computer Electr. Eng. Article ID 86492 9
[10] Feng W, He Y G, Li C L 2018 Complexity 2018 1
[11] Abuelma'Atti M T, Khalifa Z J 2016 Int.J. Electr. Eng. 53 280
Google Scholar
[12] Bao B C, Li Q D, Wang N 2016 Chaos 26 043111
Google Scholar
[13] Leonov G A, Kuznetsov N V, Vagaitsev V I 2011 Phys. Lett. A 375 2230
Google Scholar
[14] Kengne J, Negou A N, Tchiotsop D 2017 Nonlinear Dyn. 27 1
[15] Bao B C, Xu L, Wang N, Bao H, Xu Q, Chen M 2018 Int. J. Electr. Com. 94 26
Google Scholar
[16] 王伟, 曾以成, 孙睿婷 2017 66 040502
Google Scholar
Wang W, Zeng Y C, Sun R T 2017 Acta Phys. Sin. 66 040502
Google Scholar
[17] Min F H, Li C, Zhang L, Li C B 2019 Chin. J. Phys. 58 117
Google Scholar
[18] Feudel U, Kraut S 2008 Int. J. Bifurcat. Chaos 18 1607
Google Scholar
[19] Ngonghala C N, Feudel U 2011 Phys. Rev. E: Stat. Nonlinear Soft. Matter Phys. 83 056206
Google Scholar
[20] Bao H, Wang N, Bao B C, Chen M, Jin P P, Wang G Y 2018 Commun. Nonlinear Sci. Numer. Simulat. 57 264
Google Scholar
[21] Wang G Y, Yuan F, Chen G R, Zhang Y 2018 Chaos 28 013125
Google Scholar
[22] Da C, Rafael A, Eisencraf M 2019 Commun. Nonlinear Sci. Numer. Simulat. 72 441
Google Scholar
[23] Yavuz O, Erdem E 2019 Opt. Laser Technol. 114 224
Google Scholar
[24] Njitacke Z T, Kengne J 2017 Chaos, Sol. Frac. 105 77
Google Scholar
[25] Li C B, Akgul A, Sprott J C, Lu H H C, Thio W J C 2018 Int. J. Circ. Theor. Appl. 46 2434
Google Scholar
[26] Li C B, Sprott J C, Liu Y J, Gu Z Y, Zhang J W 2018 Int. J. Bifurcat. Chaos 28 1850163
Google Scholar
[27] Bao B C, Xu J P, Zhou G H, Ma Z H, Zou L 2011 Chin. Phys. B 20 109
-
图 1 电路模型 (a)磁控忆阻电路; (b)磁控忆阻等效电路
Figure 1. Circuit schematic: (a) Flux-controlled memristor circuit; (b) equivalent Circuit of flux-controlled memristor.
图 2
$y-z$ 平面上典型混沌吸引子的相图与Poincaré截面图 (a)相图; (b) Poincaré截面图Figure 2. Phase portrait and Poincaré map of typical chaotic attractor in
$y-z$ plane: (a) Phase portrait; (b) Poincaré map
图 3 随参数
$\gamma $ 变化的分岔图与Lyapunov指数谱 (a)分岔图; (b)Lyapunov指数谱Figure 3. Bifurcation and Lyapunov exponent spectrum with parameter
$\gamma $ : (a) Bifurcation diagram; (b) Lyapunov exponent spectrum
图 4 随参数c变化的分岔图与Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱
Figure 4. Bifurcation and Lyapunov exponent spectrum with parameter
$c$ : (a) Bifurcation diagram; (b) Lyapunov exponent spectrum.
图 5 双参数吸引盆 (a)参数
$\gamma -b$ ; (b)参数$c-b$ ; (c)参数$\gamma -\xi $ ; (d)参数$c-\xi $ Figure 5. Parameter mappings: (a) Parameter
$\gamma $ and$b$ ; (b) parameter$c$ and$b$ ; (c) parameter$\gamma $ and$\xi $ ; (d) parameter$c$ and$\xi $ 
图 6 不同变量组合下的共存吸引盆 (a)
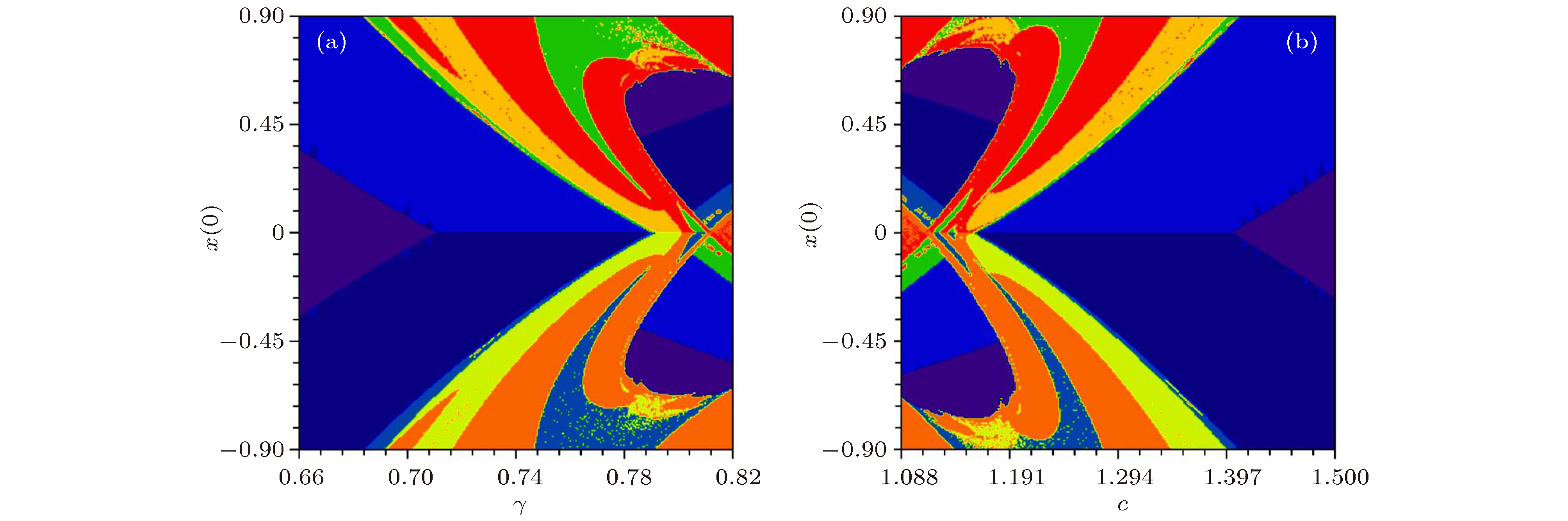
$\gamma -x\left(0\right)$ 平面, 初始条件为$\left(x\left(0\right),0,0,0\right)$ ; (b)$c-x\left(0\right)$ 平面, 初始条件为$\left(x\left(0\right),0,0,0\right)$ Figure 6. Attraction basins of coexistence in different planes: (a)
$\gamma -x\left(0\right)$ plane, with initial value of$\left(x\left( 0 \right),0,0,0\right)$ ; (b)$c-x\left(0\right)$ plane, with initial value of$\left(x\left(0\right),0,0,0\right)$ 
图 7 不同变量组合下系统状态分布图 (a)
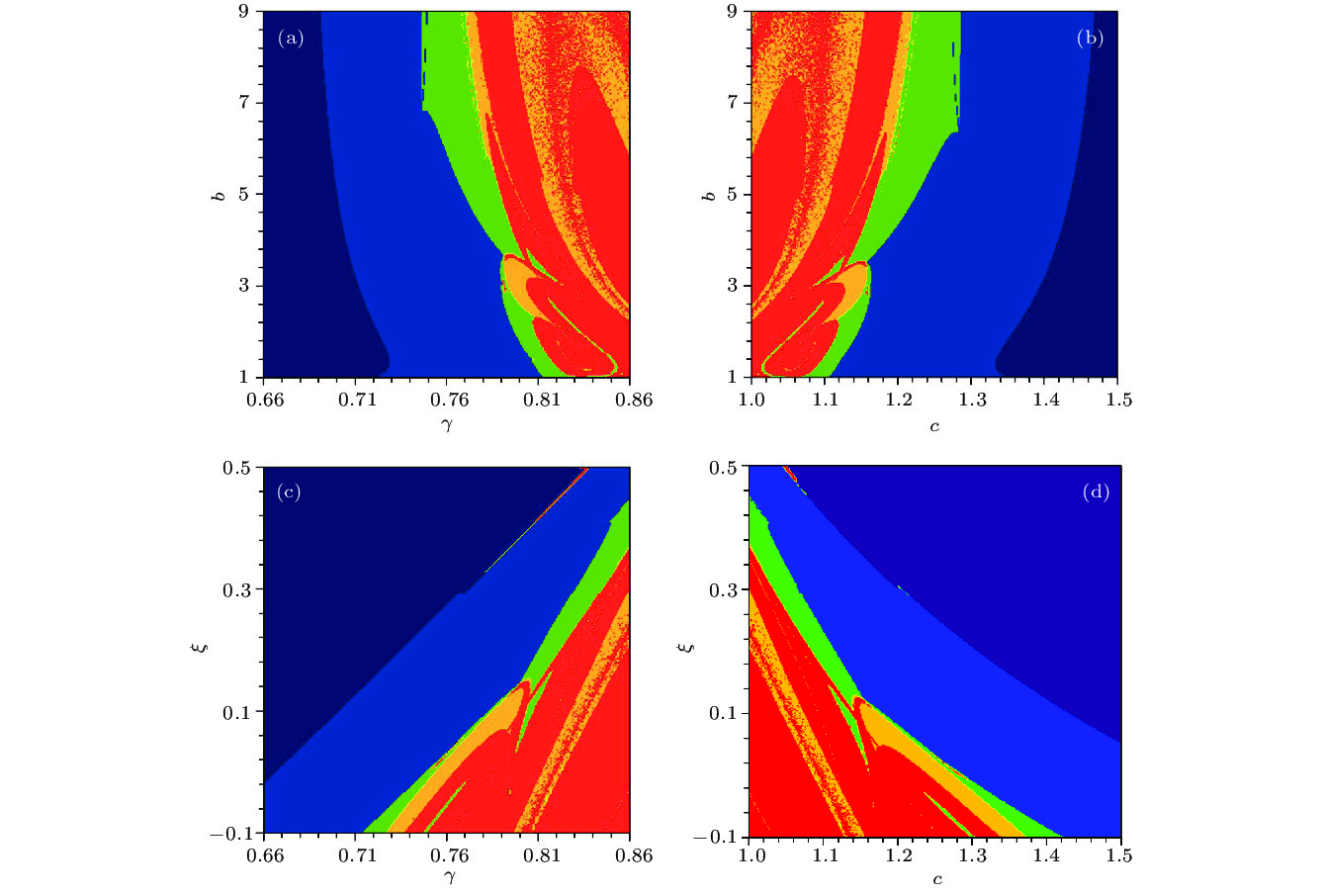
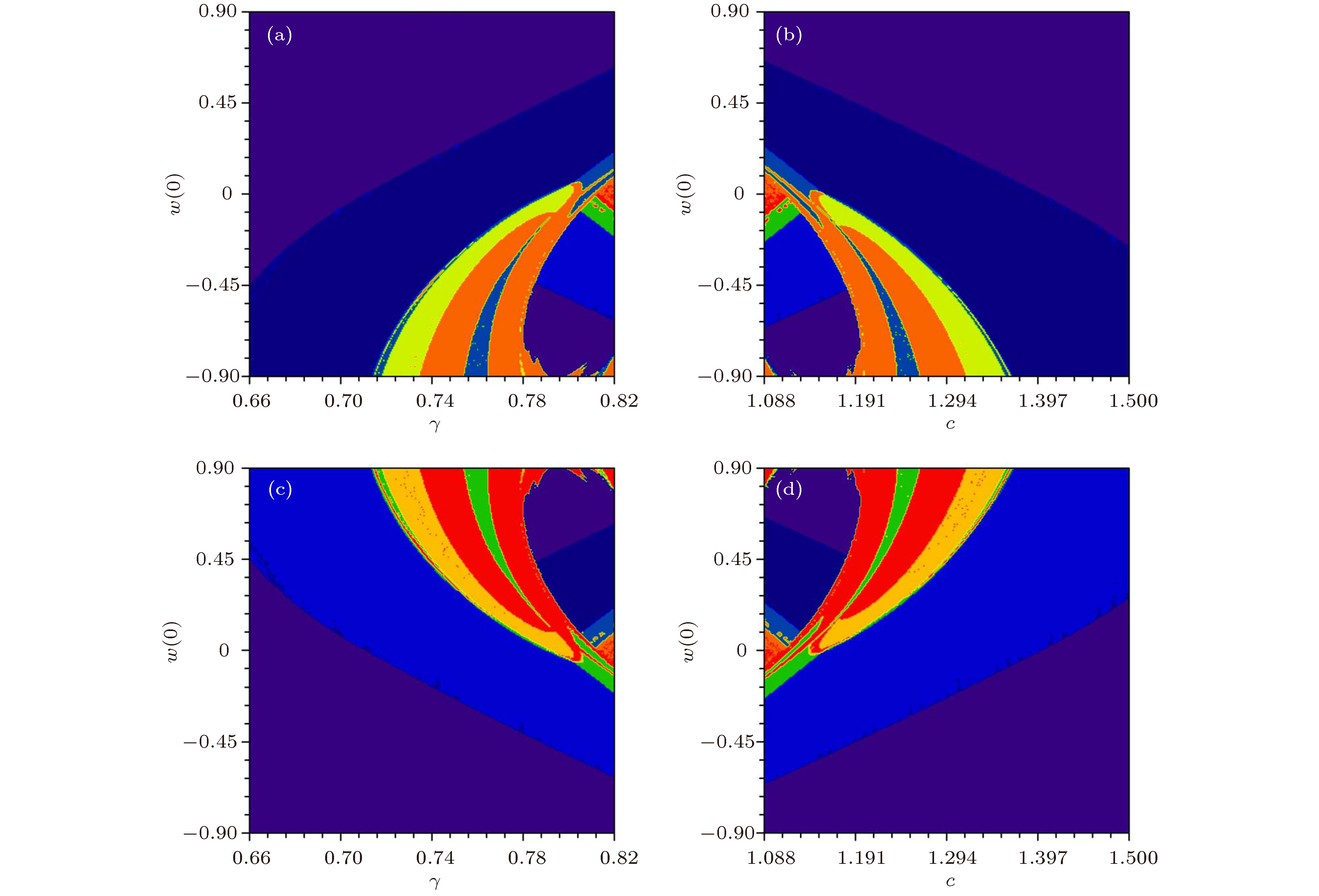
$\gamma -w(0)$ 平面, 初始条件为$( - {10^{ - 9}},0,0,w(0))$ ; (b)$c-w(0)$ 平面, 初始条件为$( - {10^{ - 9}},0,0,w(0))$ ; (c)$\gamma -w(0)$ 平面, 初始条件为$({10^{ - 9}},0,0,w(0))$ ; (d)$c-w(0)$ 平面, 初始条件为$({10^{ - 9}},0,0,w(0))$ Figure 7. Attraction basins of coexistence in different planes: (a)
$\gamma -w(0)$ plane, with initial value of$( - {10^{ - 9}},0,0,w(0))$ ; (b)$c-w(0)$ plane, with initial value of$( - {10^{ - 9}},0,0,w(0))$ ; (c)$\gamma -w(0)$ plane, with initial value of$({10^{ - 9}},0,0,w(0))$ ; (d)$c-w(0)$ plane, with initial value of$({10^{ - 9}},0,0,w(0))$ 
图 8 参数
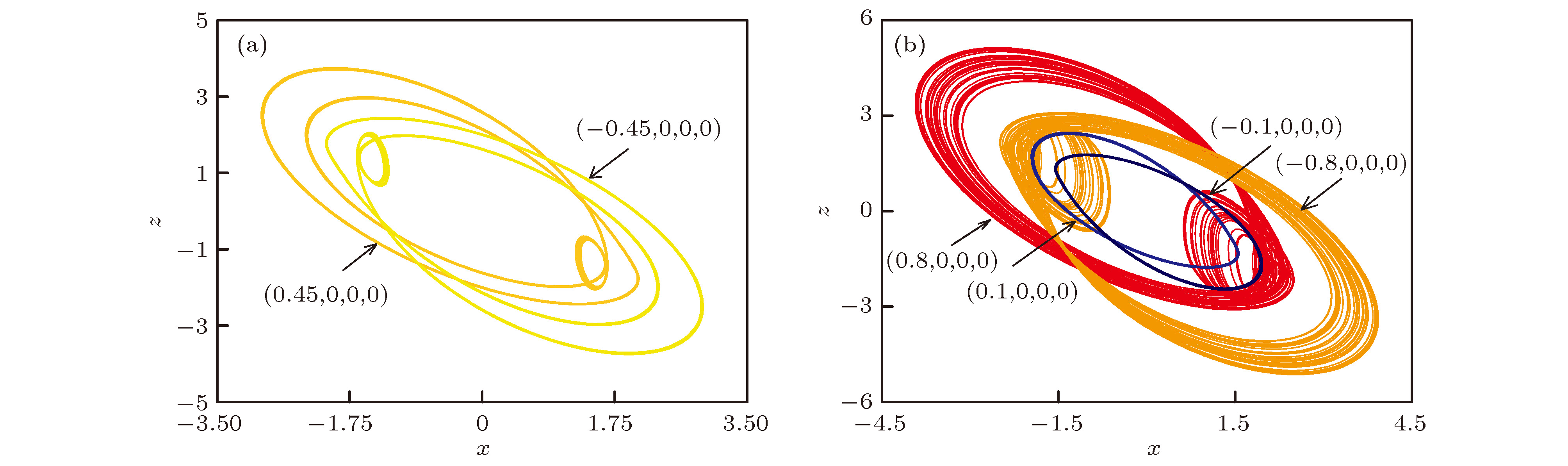
$\gamma {\rm{ = 0}}{\rm{.74}}$ ,$x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3; (b)左右共存混沌与左右共存周期1Figure 8. For different initial value, phase diagram of coexisting attractors in
$x-z$ planes when$\gamma {\rm{ = 0}}{\rm{.74}}$ : (a) Coexisting attractors of period-3; (b) coexisting attractors of chaos and period-1
图 9 参数
$c = 1.274$ ,$x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3; (b)左右共存混沌与左右共存周期1Figure 9. For different initial value, phase diagram of coexisting attractors in
$x-z$ planes when$c = 1.274$ : (a) Coexisting attractors of period-3; (b) coexisting attractors of chaos and period-1.
图 10 参数
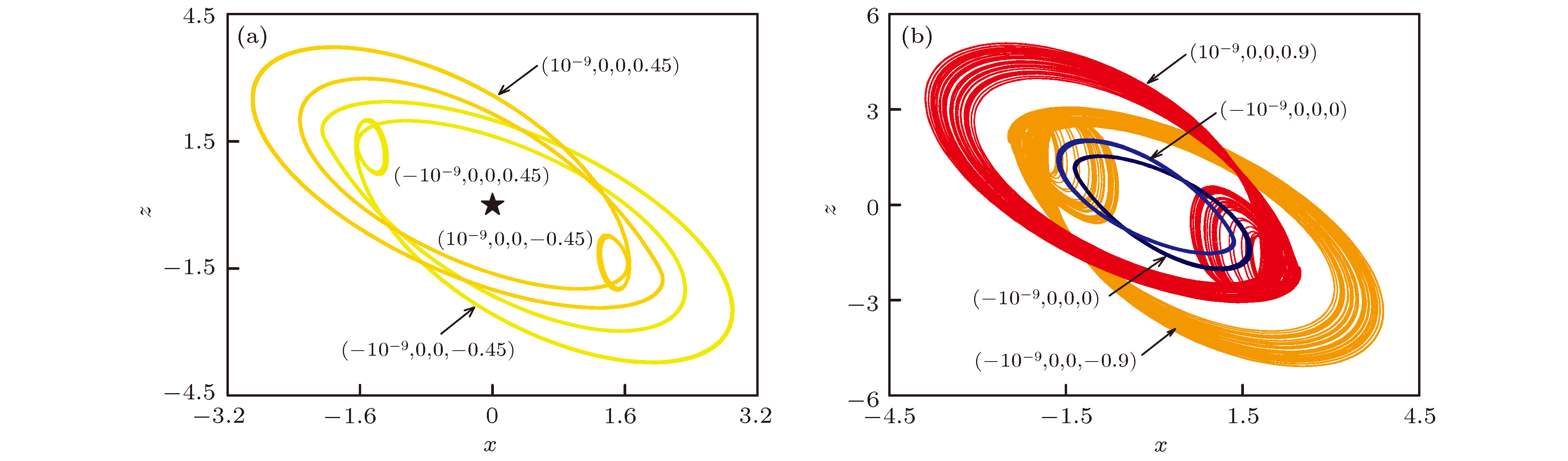
$\gamma {\rm{ = 0}}{\rm{.74}}$ ,$x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3、左右共存周期1与稳定不动点; (b)左右共存混沌与左右共存周期2Figure 10. For different initial value, phase diagram of coexisting attractors in
$x-z$ planes when$\gamma {\rm{ = 0}}{\rm{.74}}$ : (a) Coexisting attractors of period-3, period-1 and fixed point; (b) coexisting attractors of chaos and period-2
图 11 参数
$c = 1.274$ ,$x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3与稳定不动点; (b)左右共存混沌与左右共存周期1Figure 11. For different initial value, phase diagram of coexisting attractors in
$x-z$ planes when$c = 1.274$ : (a) Coexisting attractors of period-3 and fixed point; (b) coexisting attractors of chaos and period-1
图 12 顶层模块控制流程图
Figure 12. The flow chart of calling order
图 13 FPGA实物连接图与实现结果 (a)实物连接图; (b)y-z平面相图; (c)y, z两项时序图
Figure 13. The hardware connection diagram and the result of implementation: (a) The hardware connection diagram; (b) phase diagram in y-z plane; (c) timing diagram of the term y and z
图 14 固定参数
$c = 1.274$ 时x-z平面内不同初值条件下的共存, Ch1 = 500 MV, Ch2 = 500 MV (a)初值为$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , 左侧周期1; (b)初值为$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.45}}} \right)$ , 左侧周期3; (c)初值为$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.9}}} \right)$ , 左侧混沌; (d)初值为$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , 右侧周期1; (e)初值为$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.45}}} \right)$ 右侧周期3; (f)初值为$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.9}}} \right)$ , 右侧混沌Figure 14. The phase diagram of coexistence attractors with different initial conditions at
$c = 1.274$ in x-z plane, Ch1 = 500 MV, Ch2 = 500 MV: (a) The initial value as$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , left period-1; (b) the initial value as$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.45}}} \right)$ , left period-3; (c) the initial value as$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.9}}} \right)$ , left period-3; (d) the initial value as$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , right chaos; (e) the initial value as$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.45}}} \right)$ , right period-3; (f) the initial value as$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.9}}} \right)$ , right chaos表 1 系统参数
Table 1. The valueof system parameters
参数 数值 参数 数值 $a$ 1 $\xi $ 0.12 $b$ 3.5 $\alpha $ 0.3 $c$ 1 $\beta $ 0.8 $\gamma $ 0.86 
DownLoad: CSV
表 2 参数
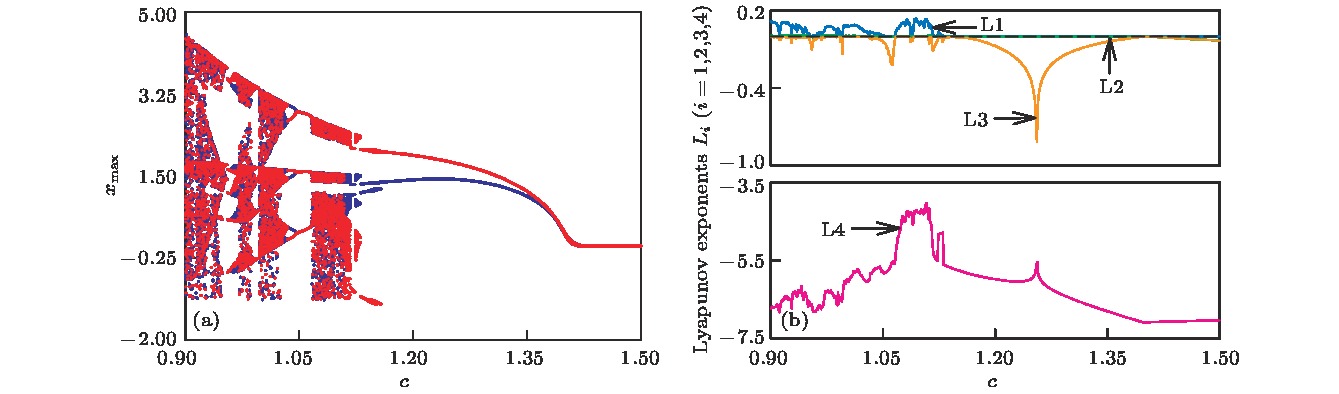
$\gamma $ , c变化时系统运动状态与对应的Lyapunov指数Table 2. The dynamic behavior and Lyapunov exponent with parameter
$\gamma $ and$c$ 参数$\gamma $ 运动状态 Lyapunov指数 $(0.6{\rm{6}},0.{\rm{704}})$ 稳定不动点 $( -, -, -, - )$ $(0.{\rm{704}},0.8{\rm{08}}) \cup (0.{\rm{829}},0.{\rm{845}})$ 周期运动 $( + , -, -, - )$ ${\rm{(0}}{\rm{.808,}}\,{\rm{0}}{\rm{.829)}} \cup {\rm{(0}}{\rm{.845,}}\,{\rm{0}}{\rm{.9)}}$ 复杂运动(混沌, 多周期) $( +,0, -, - )$ 参数c 运动状态 Lyapunov指数 ${\rm{(0}}{\rm{.9,}}\,{\rm{1}}{\rm{.02)}} \cup {\rm{(1}}{\rm{.07,1}}{\rm{.13)}}$ 复杂运动(混沌, 多周期) $( +,0, -, - )$ ${\rm{(1}}{\rm{.02,}}\,{\rm{1}}{\rm{.07)}} \cup {\rm{(1}}{\rm{.13,}}\,{\rm{1}}{\rm{.41)}}$ 周期运动 $( + , -, -, - )$ $({\rm{1}}{\rm{.41,1}}{\rm{.5}})$ 稳定不动点 $( -, -, -, - )$
DownLoad: CSV
表 3 不同颜色所对应的系统运动状态
Table 3. Colors and the corresponding system states
颜色 系统运动 紫色 稳定不动点 蓝色 周期1 绿色 周期2 黄色 周期3 红色 复杂运动(混沌, 多周期)
DownLoad: CSV
表 4 运动状态与色标的对应表
Table 4. Different colors and the corresponding dynamical state
颜色 浅蓝 
绿色 
黄色 
红色 
紫色 
共存类型 左侧周期1 左侧周期2 左侧周期3 左侧复杂运动(左侧多周期, 混沌) 稳定不动点 颜色 深蓝 
青色 
草绿 
橙色 
共存类型 右侧周期1 右侧周期2 右侧周期3 右侧复杂运动(右侧多周期, 混沌)
DownLoad: CSV
表 5 不同初值对应的共存多吸引子类型
Table 5. Coexisting multiple attractor with different initial condition
参数 吸引子类型 初始条件 $\gamma = 0.{\rm{74}}$ 左右共存点吸引子 $\left( \pm {10^{ - 9}},0,0, \mp 0.{\rm{45}}\right)$ 左右共存周期1 $\left( \pm 0.1,0,0,0\right)$,$\left( \pm {10^{ - 9}},0,0, \pm {\rm{0}}{\rm{.45}}\right)$ 左右共存周期2, 左右共存周期3 $\left( \pm {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}},0,0, \pm {\rm{0}}{\rm{.45}}\right)$, $ \left( \pm 0.{\rm{4}},0,0,0\right) $, $\left( \pm {10^{ - 9}},0,0 \pm 0.{\rm{5}}\right)$ 左右共存混沌 $\left( \pm 0.{\rm{8}},0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0, \pm 0.9\right)$ $c = 1.274$ 左右共存点吸引子 $\left( \pm {10^{ - 9}},0,0, \mp 0.{\rm{45}}\right)$ 左右共存周期1 $\left( \pm 0.1,0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0,0\right)$ 左右共存周期3 $\left( \pm 0.45,0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0 \pm 0.4{\rm{5}}\right)$ 左右共存混沌 $\left( \pm 0.{\rm{8}},0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0, \pm 0.9\right)$
DownLoad: CSV
-
[1] Chua L O 1971 IEEE Trans. Circ. Theory 18 507
Google Scholar
[2] 林毅, 刘文波, 沈骞 2018 67 230502
Google Scholar
Lin Y, Liu W B, Shen Q 2018 Acta Phys. Sin. 67 230502
Google Scholar
[3] Olumodeji O A, Gottardi M 2017 Integration 58 438
Google Scholar
[4] Joglekar Y N, Wolf S J 2009 Eur. J. Phys. 30 661
Google Scholar
[5] Guo M, Gao Z H, Xue Y B, Dou G, Li Y X 2018 Nonlinear Dyn. 93 1681
Google Scholar
[6] Wang C H, Liu X M, Xia H 2017 Chaos 27 033114
Google Scholar
[7] Peng G Y, Min F H 2017 Nonlinear Dyn. 90 1607
Google Scholar
[8] Li C, Min F H, Li C B 2018 Nonlinear Dyn. 94 2785
Google Scholar
[9] Peng G, Min F 2018 Computer Electr. Eng. Article ID 86492 9
[10] Feng W, He Y G, Li C L 2018 Complexity 2018 1
[11] Abuelma'Atti M T, Khalifa Z J 2016 Int.J. Electr. Eng. 53 280
Google Scholar
[12] Bao B C, Li Q D, Wang N 2016 Chaos 26 043111
Google Scholar
[13] Leonov G A, Kuznetsov N V, Vagaitsev V I 2011 Phys. Lett. A 375 2230
Google Scholar
[14] Kengne J, Negou A N, Tchiotsop D 2017 Nonlinear Dyn. 27 1
[15] Bao B C, Xu L, Wang N, Bao H, Xu Q, Chen M 2018 Int. J. Electr. Com. 94 26
Google Scholar
[16] 王伟, 曾以成, 孙睿婷 2017 66 040502
Google Scholar
Wang W, Zeng Y C, Sun R T 2017 Acta Phys. Sin. 66 040502
Google Scholar
[17] Min F H, Li C, Zhang L, Li C B 2019 Chin. J. Phys. 58 117
Google Scholar
[18] Feudel U, Kraut S 2008 Int. J. Bifurcat. Chaos 18 1607
Google Scholar
[19] Ngonghala C N, Feudel U 2011 Phys. Rev. E: Stat. Nonlinear Soft. Matter Phys. 83 056206
Google Scholar
[20] Bao H, Wang N, Bao B C, Chen M, Jin P P, Wang G Y 2018 Commun. Nonlinear Sci. Numer. Simulat. 57 264
Google Scholar
[21] Wang G Y, Yuan F, Chen G R, Zhang Y 2018 Chaos 28 013125
Google Scholar
[22] Da C, Rafael A, Eisencraf M 2019 Commun. Nonlinear Sci. Numer. Simulat. 72 441
Google Scholar
[23] Yavuz O, Erdem E 2019 Opt. Laser Technol. 114 224
Google Scholar
[24] Njitacke Z T, Kengne J 2017 Chaos, Sol. Frac. 105 77
Google Scholar
[25] Li C B, Akgul A, Sprott J C, Lu H H C, Thio W J C 2018 Int. J. Circ. Theor. Appl. 46 2434
Google Scholar
[26] Li C B, Sprott J C, Liu Y J, Gu Z Y, Zhang J W 2018 Int. J. Bifurcat. Chaos 28 1850163
Google Scholar
[27] Bao B C, Xu J P, Zhou G H, Ma Z H, Zou L 2011 Chin. Phys. B 20 109
DownLoad:
Catalog
Metrics
- Abstract views: 7776
- PDF Downloads: 76
- Cited By: 0
