基于Aharonov-Bohm笼的非厄米趋肤效应抑制现象

陈舒越; 蒋闯; 柯少林; 王兵; 陆培祥

doi:10.7498/aps.71.20220978

摘要

能带理论在光学领域的应用为控制光传输提供了有效手段, 非厄米趋肤效应的发现扩展了传统能带理论的范畴, 能够实现新型光局域和单向传输现象. 然而在光学体系, 如何有效地产生并调控非厄米趋肤效应仍然是重要的研究主题. 本文研究了具有规范势的准一维菱形光晶格中的非厄米趋肤效应, 通过计算本征能谱、环绕数和模式演化特性, 发现规范势能够对趋肤效应强弱进行有效调节. 当规范势大小为π时, 趋肤效应被完全抑制, 而由Aharonov-Bohm笼效应引起的平带局域占主导. 利用间接耦合微环谐振腔阵列, 可同时产生合成光子规范势和非对称耦合, 为研究Aharonov-Bohm笼和趋肤效应的竞争机制提供了可能的实现方案. 本研究结果为利用规范势调控趋肤效应提供理论基础, 在发展片上非磁性单向传播器件也具有潜在的应用前景.

关键词:

Abstract

The application of energy band theory in optics provides an effective approach to modulating the flow of light. The recent discovery of non-Hermitian skin effect promotes the development of traditional energy band theory, which further enables an alternative way to realize light localization and unidirectional propagation. However, how to effectively generate and steer the non-Hermitian skin effect is still an important topic, especially in integrated optical systems. Here, we investigate the non-Hermitian skin effect in quasi-one-dimensional rhombic optical lattice with synthetic gauge potential. By calculating the eigenenergy spectra, spectral winding number, and wave dynamics, the gauge potential can be utilized to effectively tune the localization strength of skin modes. In particular, the skin effect is completely suppressed when the gauge potential in each plaquette is equal to π, while the flat-band localization caused by Aharonov-Bohm caging effect is dominant. By utilizing the indirectly coupled micro ring resonator array, the gauge potential and asymmetric coupling can be generated at the same time, which provides a potential experimental scheme to explore the competition between Aharonov-Bohm cage and skin effect. The present study provides an alternative way to steer the skin effect, which offers an approach to achieving the on-chip non-magnetic unidirectional optical devices.

Keywords:

作者及机构信息

1.
华中科技大学物理学院, 武汉　430074

2.
武汉工程大学, 光学信息与模式识别湖北省重点实验室, 武汉　430205

通信作者: 柯少林, keshaolin@wit.edu.cn ; 王兵, wangbing@hust.edu.cn ;

基金项目: 国家自然科学基金(批准号: 11974124, 12021004)和光学信息与模式识别湖北省重点实验室开放课题研究基金(批准号: 202102)资助的课题.

Authors and contacts

1.
School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China

2.
Hubei Key Laboratory of Optical Information and Pattern Recognition, Wuhan Institute of Technology, Wuhan 430205, China

Corresponding author: Ke Shao-Lin, keshaolin@wit.edu.cn ; Wang Bing, wangbing@hust.edu.cn ;

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11974124, 12021004) and the Hubei Key Laboratory of Optical Information and Pattern Recognition (Grant No. 202102).

文章全文 : translate this paragraph

参考文献

[1]	Joannopoulos. J D, Villeneuve. P R, Fan S 1997 Nature 386 143 Google Scholar
[2]	Ke S, Zhao D, Liu J, Liu Q, Liao Q, Wang B, Lu P 2019 Opt. Express 27 13858 Google Scholar
[3]	Yuan L, Lin Q, Xiao M, Fan S 2018 Optica 5 1396 Google Scholar
[4]	Garanovich I L, Longhi S, Sukhorukov A A, Kivshar Y S 2012 Phys. Rep. 518 1 Google Scholar
[5]	Qin C, Zhou F, Peng Y, Sounas D, Zhu X, Wang B, Dong J, Zhang X, Alu A, Lu P 2018 Phys. Rev. Lett. 120 133901 Google Scholar
[6]	Mukherjee S, Spracklen A, Choudhury D, et al. 2015 Phys. Rev. Lett. 114 245504 Google Scholar
[7]	Chen H, Yang N, Qin C, et al. 2021 Light Sci. Appl. 10 48 Google Scholar
[8]	Weidemann S, Kremer M, Longhi S, Szameit A 2021 Nat. Photonics 15 576 Google Scholar
[9]	Jorg C, Queralto G, Kremer M, et al. 2020 Light Sci. Appl. 9 150 Google Scholar
[10]	Ke S, Zhao D, Fu J, Liao Q, Wang B, Lu P 2020 IEEE J. Sel. Top. Quantum Electron. 26 1 Google Scholar
[11]	Liao K, Hu X, Gan T, Liu Q, Wu Z, Fan C, Feng X, Lu C, Liu Y-c, Gong Q 2020 Adv. Opt. Photonics 12 60 Google Scholar
[12]	Leykam D, Yuan L 2020 Nanophotonics 9 4473 Google Scholar
[13]	Shang C, Chen X, Luo W, Ye F 2018 Opt. Lett. 43 275 Google Scholar
[14]	Dong J W, Chen X D, Zhu H, Wang Y, Zhang X 2017 Nat. Mater. 16 298 Google Scholar
[15]	Fang K, Yu Z, Fan S 2012 Nat. Photonics 6 782 Google Scholar
[16]	Zhou X, Lin Z K, Lu W, Lai Y, Hou B, Jiang J H 2020 Laser Photonics Rev. 14 2000010 Google Scholar
[17]	Mittal S, Orre V V, Zhu G, Gorlach M A, Poddubny A, Hafezi M 2019 Nat. Photonics 13 692 Google Scholar
[18]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[19]	Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 Google Scholar
[20]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[21]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 Google Scholar
[22]	Wang H, Ruan J, Zhang H 2019 Phys. Rev. B 99 075130 Google Scholar
[23]	Li L, Lee C H, Gong J 2020 Phys. Rev. Lett. 124 250402 Google Scholar
[24]	Liu S, Shao R, Ma S, Zhang L, You O, Wu H, Xiang Y J, Cui T J, Zhang S 2021 Research (Wash D C) 2021 5608038 Google Scholar
[25]	Zhang L, Yang Y, Ge Y, et al. 2021 Nat. Commun. 12 6297 Google Scholar
[26]	Gao P, Willatzen M, Christensen J 2020 Phys. Rev. Lett. 125 206402 Google Scholar
[27]	Wang S, Qin C, Wang B, Lu P 2018 Opt. Express 26 19235 Google Scholar
[28]	Song Y, Liu W, Zheng L, Zhang Y, Wang B, Lu P 2020 Phys. Rev. Appl. 14 064076 Google Scholar
[29]	Lin Z, Ding L, Chen S, Li S, Ke S, Li X, Wang B 2021 Phys. Rev. A 103 063507 Google Scholar
[30]	Song Y, Chen Y, Xiong W, Wang M 2022 Opt. Lett. 47 1646 Google Scholar
[31]	Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301 Google Scholar
[32]	Lu M, Zhang X X, Franz M 2021 Phys. Rev. Lett. 127 256402 Google Scholar
[33]	Peng Y, Jie J, Yu D, Wang Y 2022 arXiv: 2201.10318
[34]	Longhi S 2014 Opt. Lett. 39 5892 Google Scholar
[35]	Mukherjee S, Thomson R R 2015 Opt. Lett. 40 5443 Google Scholar
[36]	Kremer M, Petrides I, Meyer E, Heinrich M, Zilberberg O, Szameit A 2020 Nat. Commun. 11 907 Google Scholar
[37]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[38]	Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 Google Scholar
[39]	Wang P, Jin L, Song Z 2019 Phys. Rev. A 99 062112 Google Scholar
[40]	Zhang Z X, Huang R, Qi L, Xing Y, Zhang Z J, Wang H F 2020 Ann. Phys. 533 2000272 Google Scholar
[41]	Hafezi M, Demler E A, Lukin M D, Taylor J M 2011 Nat. Phys. 7 907 Google Scholar
[42]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar

施引文献

图 1 准一维非厄米菱形晶格示意图

Fig. 1. Schematic of non-Hermitian quasi-one-dimensional rhombic chain.

下载: 全尺寸图片幻灯片

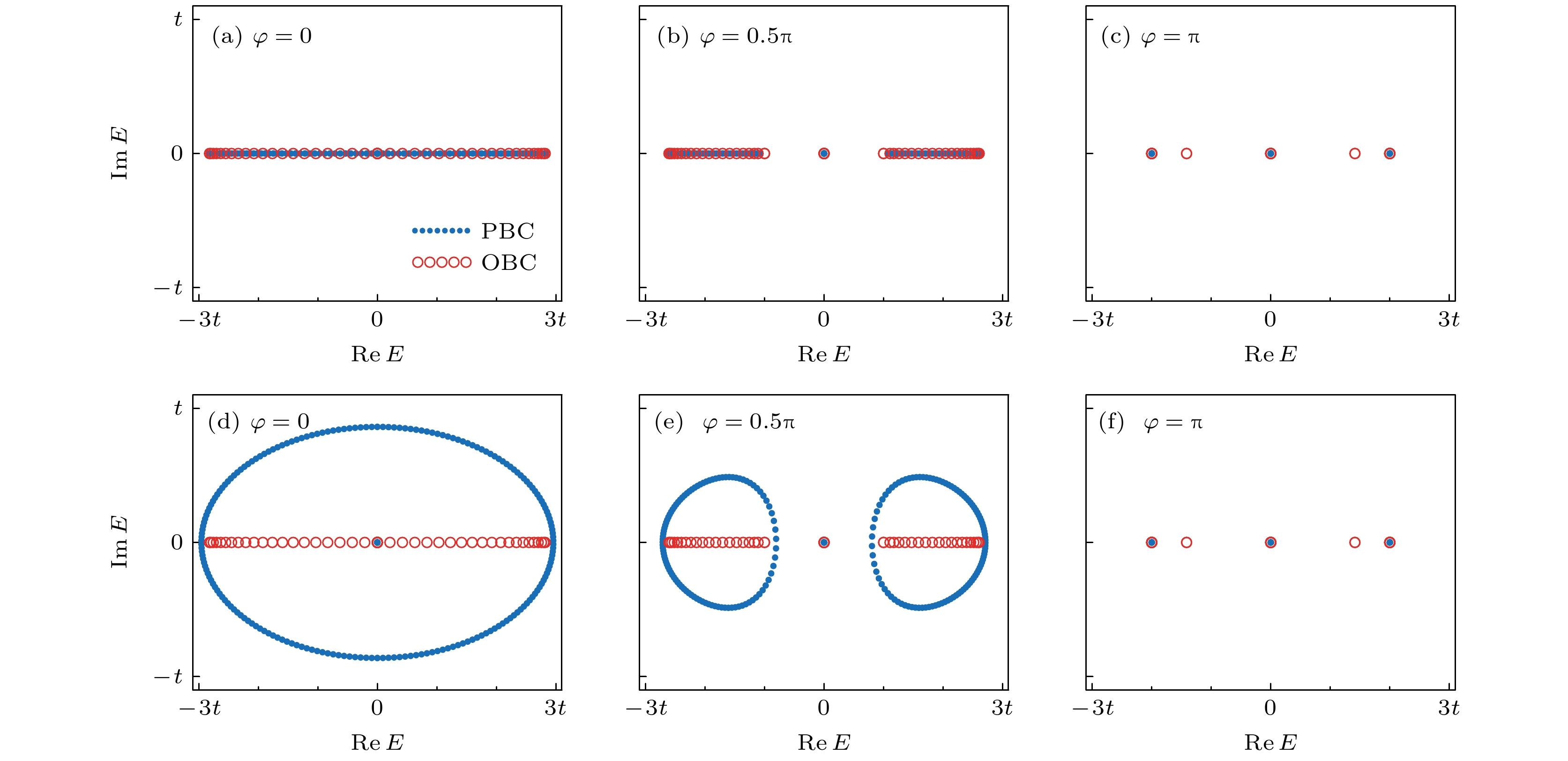
图 2 周期边界条件(蓝色实心圆)和开放边界条件(红色空心圆)下的复能谱　(a)—(c) 分别对应厄米情况下(h = 0)规范势 φ = 0, 0.5π, π 的能谱图; (d)—(f) 分别对应非厄米情况下(h = 0.6)规范势 φ = 0, 0.5π, π 的能谱图

Fig. 2. Complex energy spectra under periodic (blue solid circles) and open boundary conditions (red hollow circles): (a)–(c) Energy spectra for Hermitian cases (h = 0) with φ = 0, 0.5π, π, respectively; (d)–(f) energy spectra for non-Hermitian cases (h = 0.6) with φ = 0, 0.5π, π, respectively.

下载: 全尺寸图片幻灯片

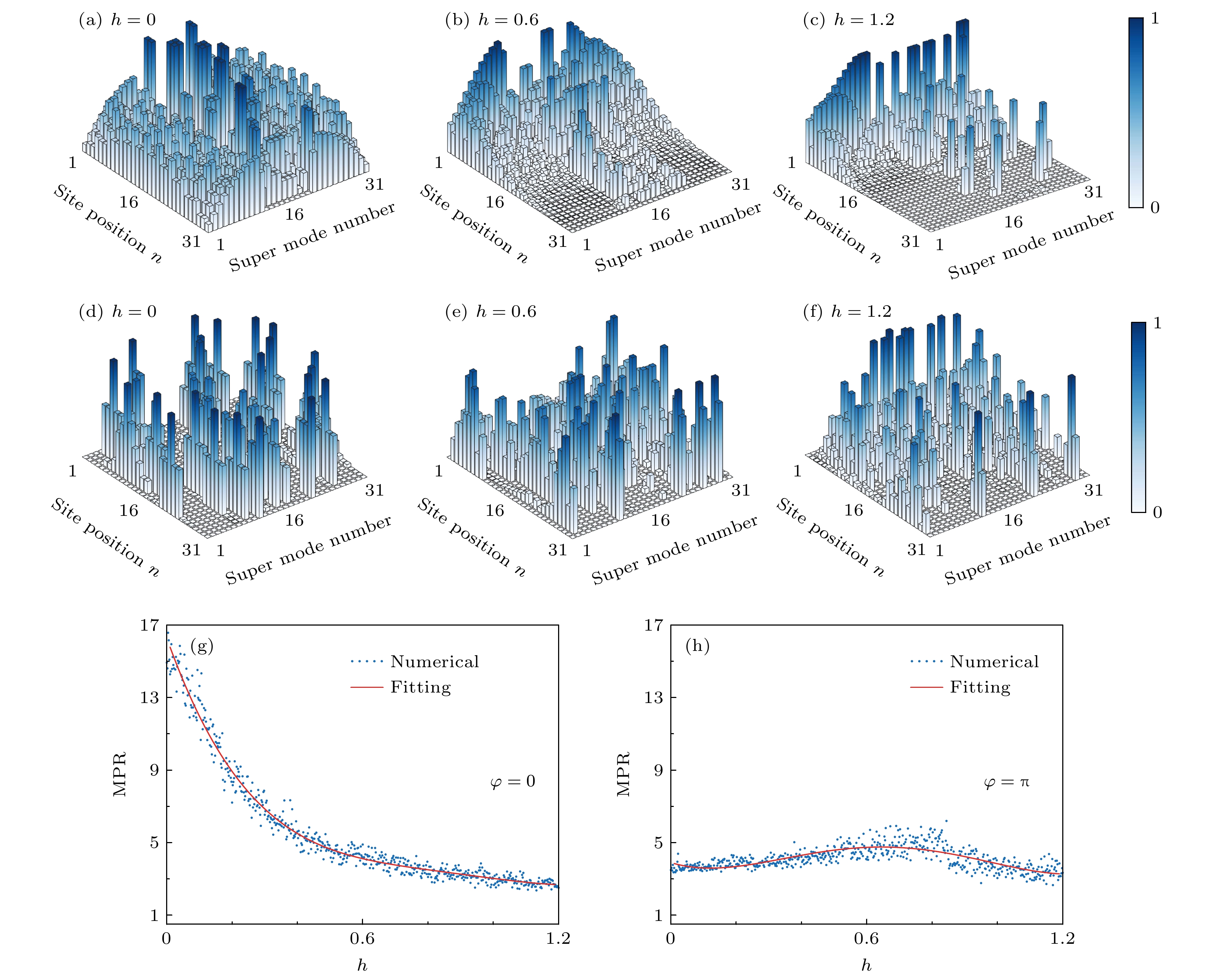
图 3 不同参数下的本征模式分布和MPR变化　(a)—(c) φ = 0时, h 取0, 0.6, 1.2时的本征模式分布; (d)—(f) φ = π时, h 取0, 0.6, 1.2时的本征模式分布; (g) 规范势 φ = 0 时MPR随h变化情况; (h) 规范势 φ = π 时MPR随h变化情况; 蓝色圆点表示数值计算的结果, 红色实线表示回归分析的结果

Fig. 3. The distribution of eigenmodes and the variation of MPR via h under different parameters: (a)–(c) the distributions of eigenmodes with φ = 0 as h = 0, 0.6, and 1.2, respectively; (d)–(f) the distributions of eigenmodes with φ = π as h = 0, 0.6, and 1.2, respectively; (g) MPR as a function of h for φ = 0; (h) MPR as a function of h for φ = π. The blue dots indicate the result of numerical calculation and the red solid lines indicate the result of regression.

下载: 全尺寸图片幻灯片

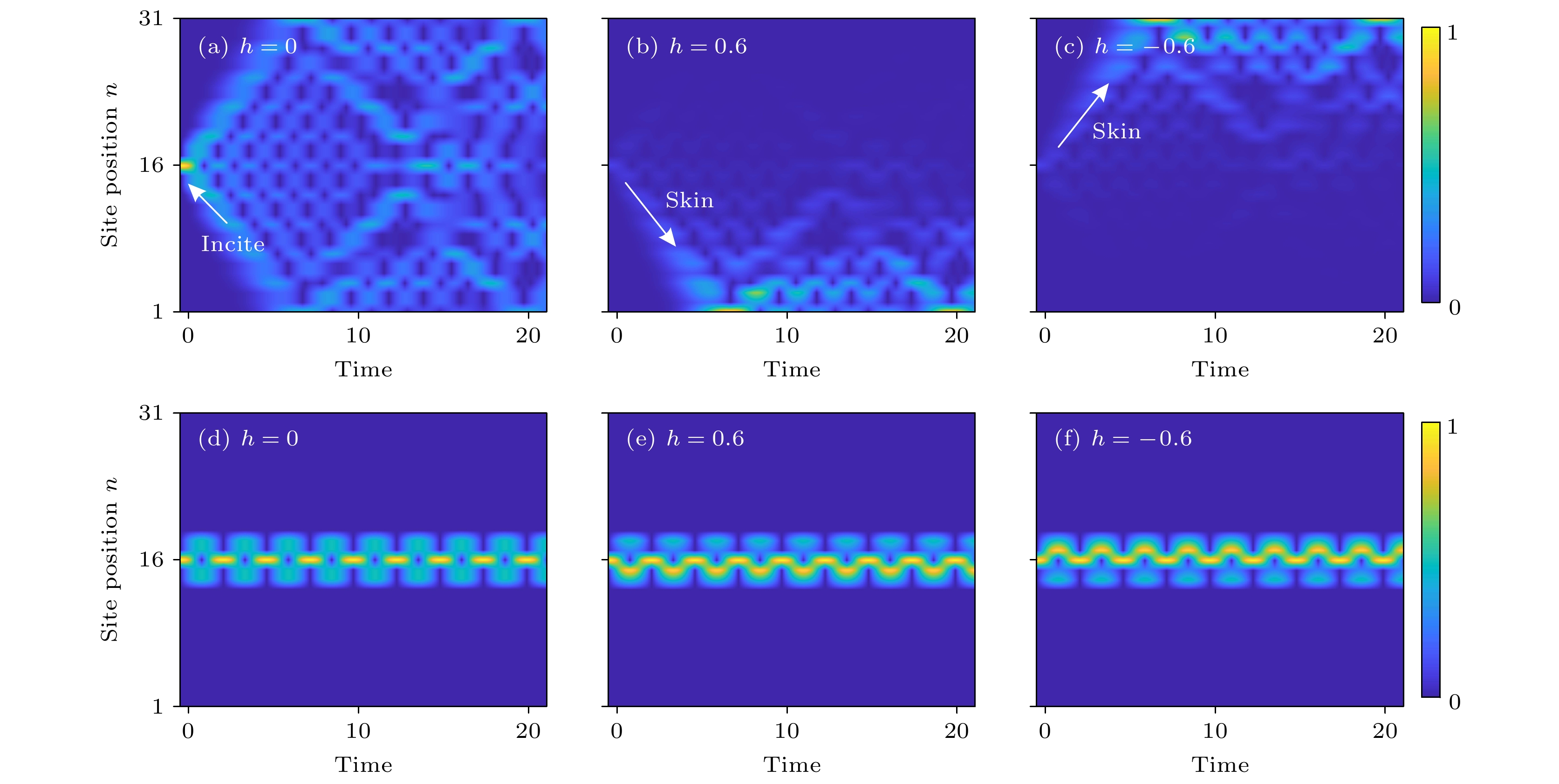
图 4 不同参数下的单点激发随时间演化特性　(a)—(c) 规范势 φ = 0 时h 分别取0, 0.6, –0.6时的演化; (d)—(f) 规范势 φ = π 时h 分别取0, 0.6, –0.6时的演化

Fig. 4. Time-dependent wave dynamics for single-site injection with different parameters: (a)–(c) For φ = 0 with h = 0, 0.6, –0.6, respectively; (d)–(f) for φ = π with h = 0, 0.6, –0.6, respectively.

下载: 全尺寸图片幻灯片

图 5 单点激发下一段时间演化后(时间取20)的输出模场分布随规范势φ的变化情况. 格点总数N = 31, 激发位置始终位于结构的正中间A格点(n = 16), 选取固定不变的趋肤强度h = 0.6, 模场强度已做归一化处理

Fig. 5. The variation of the output field distribution with the gauge potential φ after a period of evolution under single-site excitation (Time is 20). The total number of site N = 31. The field is incident from the middle A site of the structure (n = 16), the skin strength is fixed at h = 0.6, and the intensity of the field is normalized.

下载: 全尺寸图片幻灯片

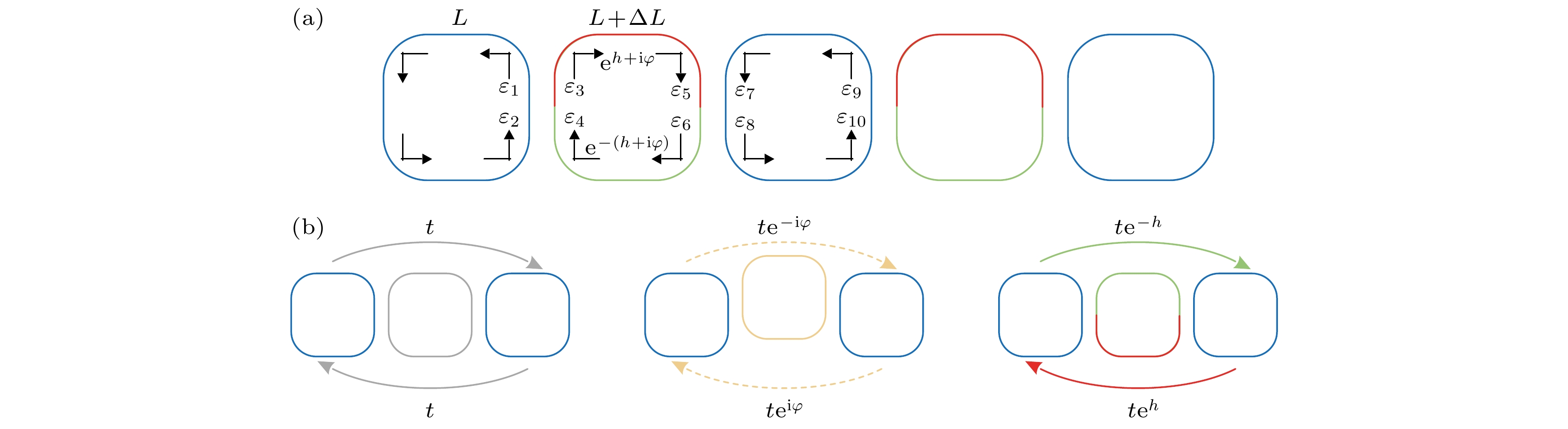
图 6 微环耦合特性示意图　(a) 一维环形谐振腔阵列演示传输矩阵法的原理示意图; (b) 利用连接环实现不同类型的耦合

Fig. 6. Schematic diagram of microring coupling characteristics: (a) Schematic diagram of the 1D array of ring resonators to demonstrate the principle of the transmission matrix method; (b) implementation of different types of coupling using link rings.

下载: 全尺寸图片幻灯片

图 7 耦合微环谐振腔阵列的趋肤效应模拟结果　(a) 菱形微环谐振腔阵列示意图; (b)—(g) 分别展示了规范势φ和用于引入增益损耗的折射率虚部大小γ取不同值时的模场强度空间分布(|E|²); (h) S21随φ的变化趋势

Fig. 7. Simulation results based on coupled resonator arrays: (a) Geometry of non-Hermitian quasi 1D rhombic chain with ring resonator arrays; (b)–(g) the spatial intensity (|E|²) distributions of light with different values of gauge potential φ and the imaginary index γ used to introduce gain and loss; (h) the trend of S21 with φ.

下载: 全尺寸图片幻灯片

map

[1]	Joannopoulos. J D, Villeneuve. P R, Fan S 1997 Nature 386 143 Google Scholar
[2]	Ke S, Zhao D, Liu J, Liu Q, Liao Q, Wang B, Lu P 2019 Opt. Express 27 13858 Google Scholar
[3]	Yuan L, Lin Q, Xiao M, Fan S 2018 Optica 5 1396 Google Scholar
[4]	Garanovich I L, Longhi S, Sukhorukov A A, Kivshar Y S 2012 Phys. Rep. 518 1 Google Scholar
[5]	Qin C, Zhou F, Peng Y, Sounas D, Zhu X, Wang B, Dong J, Zhang X, Alu A, Lu P 2018 Phys. Rev. Lett. 120 133901 Google Scholar
[6]	Mukherjee S, Spracklen A, Choudhury D, et al. 2015 Phys. Rev. Lett. 114 245504 Google Scholar
[7]	Chen H, Yang N, Qin C, et al. 2021 Light Sci. Appl. 10 48 Google Scholar
[8]	Weidemann S, Kremer M, Longhi S, Szameit A 2021 Nat. Photonics 15 576 Google Scholar
[9]	Jorg C, Queralto G, Kremer M, et al. 2020 Light Sci. Appl. 9 150 Google Scholar
[10]	Ke S, Zhao D, Fu J, Liao Q, Wang B, Lu P 2020 IEEE J. Sel. Top. Quantum Electron. 26 1 Google Scholar
[11]	Liao K, Hu X, Gan T, Liu Q, Wu Z, Fan C, Feng X, Lu C, Liu Y-c, Gong Q 2020 Adv. Opt. Photonics 12 60 Google Scholar
[12]	Leykam D, Yuan L 2020 Nanophotonics 9 4473 Google Scholar
[13]	Shang C, Chen X, Luo W, Ye F 2018 Opt. Lett. 43 275 Google Scholar
[14]	Dong J W, Chen X D, Zhu H, Wang Y, Zhang X 2017 Nat. Mater. 16 298 Google Scholar
[15]	Fang K, Yu Z, Fan S 2012 Nat. Photonics 6 782 Google Scholar
[16]	Zhou X, Lin Z K, Lu W, Lai Y, Hou B, Jiang J H 2020 Laser Photonics Rev. 14 2000010 Google Scholar
[17]	Mittal S, Orre V V, Zhu G, Gorlach M A, Poddubny A, Hafezi M 2019 Nat. Photonics 13 692 Google Scholar
[18]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[19]	Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 Google Scholar
[20]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[21]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 Google Scholar
[22]	Wang H, Ruan J, Zhang H 2019 Phys. Rev. B 99 075130 Google Scholar
[23]	Li L, Lee C H, Gong J 2020 Phys. Rev. Lett. 124 250402 Google Scholar
[24]	Liu S, Shao R, Ma S, Zhang L, You O, Wu H, Xiang Y J, Cui T J, Zhang S 2021 Research (Wash D C) 2021 5608038 Google Scholar
[25]	Zhang L, Yang Y, Ge Y, et al. 2021 Nat. Commun. 12 6297 Google Scholar
[26]	Gao P, Willatzen M, Christensen J 2020 Phys. Rev. Lett. 125 206402 Google Scholar
[27]	Wang S, Qin C, Wang B, Lu P 2018 Opt. Express 26 19235 Google Scholar
[28]	Song Y, Liu W, Zheng L, Zhang Y, Wang B, Lu P 2020 Phys. Rev. Appl. 14 064076 Google Scholar
[29]	Lin Z, Ding L, Chen S, Li S, Ke S, Li X, Wang B 2021 Phys. Rev. A 103 063507 Google Scholar
[30]	Song Y, Chen Y, Xiong W, Wang M 2022 Opt. Lett. 47 1646 Google Scholar
[31]	Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301 Google Scholar
[32]	Lu M, Zhang X X, Franz M 2021 Phys. Rev. Lett. 127 256402 Google Scholar
[33]	Peng Y, Jie J, Yu D, Wang Y 2022 arXiv: 2201.10318
[34]	Longhi S 2014 Opt. Lett. 39 5892 Google Scholar
[35]	Mukherjee S, Thomson R R 2015 Opt. Lett. 40 5443 Google Scholar
[36]	Kremer M, Petrides I, Meyer E, Heinrich M, Zilberberg O, Szameit A 2020 Nat. Commun. 11 907 Google Scholar
[37]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[38]	Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 Google Scholar
[39]	Wang P, Jin L, Song Z 2019 Phys. Rev. A 99 062112 Google Scholar
[40]	Zhang Z X, Huang R, Qi L, Xing Y, Zhang Z J, Wang H F 2020 Ann. Phys. 533 2000272 Google Scholar
[41]	Hafezi M, Demler E A, Lukin M D, Taylor J M 2011 Nat. Phys. 7 907 Google Scholar
[42]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar

[1]	胡飞飞, 李思莹, 朱顺, 黄昱, 林旭斌, 张思拓, 范云茹, 周强, 刘云. 用于量子纠缠密钥的多波长对量子关联光子对产生. , 2024, 73(23): 230304. doi: 10.7498/aps.73.20241274
[2]	黄泽鑫, 圣宗强, 程乐乐, 曹三祝, 陈华俊, 吴宏伟. 一维非互易声学晶体的非厄米趋肤态操控. , 2024, 73(21): 214301. doi: 10.7498/aps.73.20241087
[3]	徐灿鸿, 许志聪, 周子榆, 成恩宏, 郎利君. 非厄米格点模型的经典电路模拟. , 2023, 72(20): 200301. doi: 10.7498/aps.72.20230914
[4]	刘宇航, 林曈, 李少波, 于文琦, 马向, 梁晓东, 恽斌峰. 可调反射器辅助的可重构微环光滤波器. , 2023, 72(8): 084208. doi: 10.7498/aps.72.20222384
[5]	赵艳军, 谭宁, 王堉琪, 郑亚锐, 王辉, 刘伍明. 规范势下正方形格点超导量子比特电路中的量子态输运. , 2023, 72(10): 100304. doi: 10.7498/aps.72.20222349
[6]	杨艳丽, 段志磊, 薛海斌. 非厄米Su-Schrieffer-Heeger链边缘态和趋肤效应依赖的电子输运特性. , 2023, 72(24): 247301. doi: 10.7498/aps.72.20231286
[7]	成恩宏, 郎利君. 非互易Aubry-André 模型的经典电路模拟. , 2022, 71(16): 160301. doi: 10.7498/aps.71.20220219
[8]	侯博, 曾琦波. 非厄米镶嵌型二聚化晶格. , 2022, 71(13): 130302. doi: 10.7498/aps.71.20220890
[9]	刘佳琳, 庞婷方, 杨孝森, 王正岭. 无序非厄米Su-Schrieffer-Heeger中的趋肤效应. , 2022, 71(22): 227402. doi: 10.7498/aps.71.20221151
[10]	邓天舒. 畴壁系统中的非厄米趋肤效应. , 2022, 71(17): 170306. doi: 10.7498/aps.71.20221087
[11]	胡渝民, 宋飞, 汪忠. 广义布里渊区与非厄米能带理论. , 2021, 70(23): 230307. doi: 10.7498/aps.70.20211908
[12]	肖金标, 罗辉, 徐银, 孙小菡. 硅基槽式微环谐振腔型偏振解复用器全矢量分析. , 2015, 64(19): 194207. doi: 10.7498/aps.64.194207
[13]	吉喆, 贾大功, 张红霞, 张德龙, 刘铁根, 张以谟. 结构参数对串联微环谐振腔编解码器性能的影响. , 2015, 64(3): 034218. doi: 10.7498/aps.64.034218
[14]	曹彤彤, 张利斌, 费永浩, 曹严梅, 雷勋, 陈少武. 基于Add-drop型微环谐振腔的硅基高速电光调制器设计. , 2013, 62(19): 194210. doi: 10.7498/aps.62.194210
[15]	栗军, 刘玉, 平婧, 叶银, 李新奇. 双量子点Aharonov-Bohm干涉系统输运性质的大偏离分析. , 2012, 61(13): 137202. doi: 10.7498/aps.61.137202
[16]	吴丽君, 韩宇, 公卫江, 谭天亚. 量子点环嵌入Aharonov-Bohm干涉器中电子的退耦合态及反共振现象. , 2011, 60(10): 107303. doi: 10.7498/aps.60.107303
[17]	蔡鑫伦, 黄德修, 张新亮. 基于全矢量模式匹配法的三维弯曲波导本征模式计算. , 2007, 56(4): 2268-2274. doi: 10.7498/aps.56.2268
[18]	吴绍全, 孙威立, 余万伦, 王顺金. 嵌入单量子点Aharonov-Bohm环中的近藤效应. , 2005, 54(6): 2910-2917. doi: 10.7498/aps.54.2910
[19]	吴绍全, 谌雄文, 孙威立, 王顺金. 嵌入耦合量子点的介观Aharonov-Bohm环内的持续电流. , 2004, 53(7): 2336-2341. doi: 10.7498/aps.53.2336
[20]	叶剑斐, 叶飞, 丁国辉. 嵌入量子点的介观Aharonov-Bohm环的基态与持续电流. , 2003, 52(2): 468-472. doi: 10.7498/aps.52.468

计量

文章访问数: 5277
PDF下载量: 306
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于Aharonov-Bohm笼的非厄米趋肤效应抑制现象