-
在非互易Su-Schrieffer-Heeger (SSH)链中, 电子在胞内的跳跃振幅依赖于其跳跃方向, 因而, 该非厄米SSH链同时存在非平庸拓扑边缘态和非厄米趋肤效应. 相应地, 如何探测非厄米SSH链的边缘态和趋肤效应成为非厄米物理学的一个重要课题. 本文研究了非厄米SSH链的非平庸拓扑边缘态和非厄米趋肤效应对其零能附近电子输运特性的依赖关系. 研究发现当电子在零能附近透射率峰的峰值远小于1时, 非厄米SSH链具有左趋肤效应; 反之, 零能附近电子透射率峰的峰值远大于1时, 非厄米SSH链则具有右趋肤效应. 特别是, 在非平庸拓扑边缘态区域内, 非厄米SSH链的趋肤效应被进一步增强. 另外, 当非厄米SSH链与左、右导线之间的电子隧穿耦合强度由弱到强改变时, 零能附近电子反射率谷的数目将从2个变为0, 此特性可以用来探测非厄米SSH链具有非平庸拓扑边缘态. 上述结果在理论上为探测非厄米SSH链的非平庸拓扑边缘态和非厄米趋肤效应类型提供了一种可选择的方案.
-
关键词:
- 边缘态 /
- 非厄米趋肤效应 /
- 非厄米Su-Schrieffer-Heeger链 /
- 反射率 /
- 透射率
In the non-reciprocal Su-Schrieffer-Heeger (SSH) chain, the hopping amplitude of an electron in the intra-cell depends on its hopping direction. Consequently, the non-Hermitian SSH chain has both non-trivial topological edge state and non-Hermitian skin effect. However, how to detect the non-trivial topological edge states and non-Hermitian skin effect has become an important topic in non-Hermitian physics. In this paper, we study the relationships of the non-trivial topological edge states and the non-Hermitian skin effect of non-Hermitian SSH chain with their electron transport properties in the vicinity of the zero energy. It is demonstrated that when the peak value of the electron transmission probability in the vicinity of the zero energy is much smaller than 1, the non-Hermitian SSH chain has a left-non-Hermitian skin effect; while that in the vicinity of the zero energy is much larger than 1, the non-Hermitian SSH chain has a right-non-Hermitian skin effect. In particular, the skin effect of non-Hermitian SSH chain can be further enhanced in the region of non-trivial topological edge states. Moreover, with the increase of the electron tunneling coupling amplitudes between the non-Hermitian SSH chain and the left and right leads from the weak coupling regime to the strong coupling one, the number of the dips of reflection probability in the vicinity of the zero energy will change from two to zero. Therefore, these results theoretically provide an alternative scheme for detecting non-trivial topological edge states and non-Hermitian skin effect types of the non-Hermitian SSH chain.-
Keywords:
- edge states /
- non-Hermitian skin effect /
- non-Hermitian Su-Schrieffer-Heeger chain /
- reflection probability /
- transmission probability
[1] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
Google Scholar
[2] Bergholtz E J, Budich J C, K Flore K 2021 Rev. Mod. Phys. 93 015005
Google Scholar
[3] Zhang X, Zhang T, Lu M H, Chen Y F 2022 Adv. Phys. -X 7 2109431
Google Scholar
[4] Li A, Wei H, Cotrufo M, Chen W, Mann S, Ni X, Xu B, Chen J, Wang J, Fan S, Qiu CW, Alù A, Chen L 2023 Nat. Nanotechnol. 18 706
Google Scholar
[5] Banerjee A, Sarkar R, Dey S, Narayan A 2023 J. Phys. Condens. Matter 35 333001
Google Scholar
[6] Heiss W D 2012 J. Phys. A: Math. Theor. 45 444016
Google Scholar
[7] Mandal I, Bergholtz E J, 2021 Phys. Rev. Lett. 127 186601
Google Scholar
[8] Wang Q, Chong Y D 2023 J. Opt. Soc. Am. B 40 1443
Google Scholar
[9] Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, ThomaleR 2020 Nat. Phys. 16 747
Google Scholar
[10] Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761
Google Scholar
[11] Ghataka A, Brandenbourgera M, van Wezela J, Coulaisa C 2020 Proc. Natl. Acad. Sci. U. S. A. 117 29561
Google Scholar
[12] Lee T E 2016 Phys. Rev. Lett. 116 133903
Google Scholar
[13] Jin L, Song Z 2019 Phys. Rev. B 99 081103(R
Google Scholar
[14] Wang X R, Guo C X, Kou S P 2020 Phys. Rev. B 101 121116(R
Google Scholar
[15] Wang X R, Guo C X, Du Q, Kou S P 2020 Chin. Phys. Lett. 37 117303
Google Scholar
[16] Jezequel L, Delplace P 2023 Phys. Rev. Lett. 130 066601
Google Scholar
[17] Zeuner J M, Rechtsman M C, Plotnik Y, Lumer Y, Nolte S, Rudner M S, Segev M, SzameitA 2015 Phys. Rev. Lett. 115 040402
Google Scholar
[18] Weimann S, Kremer M, Plotnik Y, Lumer Y, Nolte S, Makris K G, Segev M, Rechtsman M C, Szameit A 2017 Nat. Mater. 16 433
Google Scholar
[19] Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311
Google Scholar
[20] Liu S, Shao R, Ma S, Zhang L, You O, Wu H, Xiang Y J, Cui T J, Zhang S 2021 Research 2021 5608038
Google Scholar
[21] Liang Q, Xie D, Dong Z, Li H, Li H, Gadway B, Yi W, Yan B 2022 Phys. Rev. Lett. 129 070401
Google Scholar
[22] Zhou Q, Wu J, Pu Z, Lu J, Huang X, Deng W, Ke M, Liu Z, 2023 Nat. Commun. 14 4569
Google Scholar
[23] Feng Y, Liu Z, Liu F, Yu J, Liang S, Li F, Zhang Y, Xiao M, Zhang Z 2023 Phys. Rev. Lett. 131 013802
Google Scholar
[24] Zhang H, Chen T, Li L, Lee C H, Zhang X 2023 Phys. Rev. B 107 085426
Google Scholar
[25] Lee C H, Thomale R 2019 Phys. Rev. B 99 201103(R
Google Scholar
[26] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801
Google Scholar
[27] Lin Z, Lin Y, Yi W 2022 Phys. Rev. B 106 063112
Google Scholar
[28] Zeng Q B 2022 Phys. Rev. B 106 235411
Google Scholar
[29] Li J R, Luo C, Zhang L L, Zhang S F, Zhu P P, Gong W J 2023 Phys. Rev. A 107 022222
Google Scholar
[30] Tang C, Yang H, Song L, Yao X, Yan P, Cao Y 2023 Phys. Rev. B 108 035410
Google Scholar
[31] Kokhanchik P, Solnyshkov D, MalpuechG 2023 Phys. Rev. B 108 L041403
Google Scholar
[32] Su W P, SchriefferJ R, HeegerA J 1980 Phys. Rev. B 22 2099
Google Scholar
[33] Li H, Yi W 2022 Phys. Rev. A 106 053311
Google Scholar
[34] 张蓝云, 薛海斌, 陈彬, 陈建宾, 邢丽丽 2020 69 077301
Google Scholar
Zhang L Y, Xue H B, Chen B, Chen J B, Xing L L 2020 Acta Phys. Sin. 69 077301
Google Scholar
[35] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽 2021 70 087301
Google Scholar
Xue H B, Duan Z L, Chen B, Chen J B, Xing L L 2021 Acta Phys. Sin. 70 087301
Google Scholar
[36] Ye C Z, Zhang L Y, Xue H B 2022 Chin. Phys. B 31 027304
Google Scholar
[37] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
-
图 1 非厄米SSH链与左、右导线耦合系统的示意图, 其中, 小的实心圆(红色)表示A子格, 大的实心圆(绿色)表示B子格, 空心圆(黑色)表示导线上的原子
Fig. 1. Schematic diagram of the non-Hermitian SSH chain coupled to the left and right leads. The small solid circles (red) represent the A sublattices, the large solid circles (green) represent the B sublattices, the hollow circles (black) represent atoms on the leads.
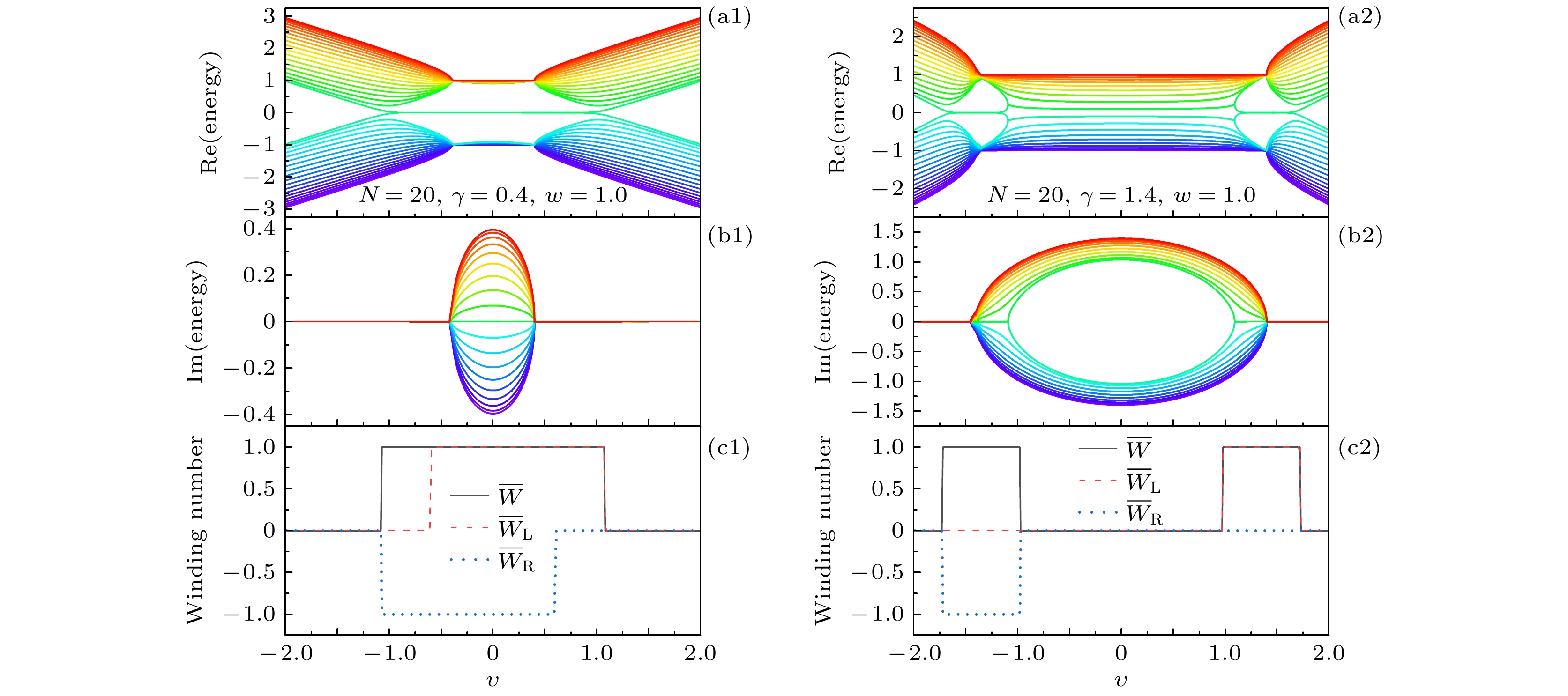
图 2 (a1), (a2)非厄米SSH链的能谱图实部; (b1), (b2)非厄米SSH链的能谱图虚部; (c1), (c2)非厄米SSH链的不同缠绕数随着$ \upsilon $的变化图. 其中, (a1), (b1), (c1) $ \gamma = 0.4 $; (a2), (b2)和(c2) $ \gamma = 1.4 $. 非厄米SSH链的其他参数选取为$ w = 1.0 $, $ N = 20 $
Fig. 2. (a1), (a2) Real part of the energy spectrum of the non-Hermitian SSH chain; (b1), (b2) imaginary part of the energy spectrum of the non-Hermitian SSH chain; (c1), (c2) the different winding number of the non-Hermitian SSH chain as a function of the value of $\upsilon $. Here, (a1), (b1), (c1) $ \gamma = 0.4 $; (a2), (b2), (c2) $ \gamma = 1.4 $. The other parameters of the non-Hermitian SSH chain are chosen as $ w = 1.0 $ and $ N = 20 $.
图 3 非厄米SSH链在零能附近的本征值的本征态波函数概率幅的绝对值随子格$n$和$ \upsilon $值变化的相图 (a) $\gamma = $$ 0.4$; (b) $\gamma = 1.4$; 非厄米SSH链的其他参数选取为$ w = $$ 1.0 $, $ N = 20 $
Fig. 3. Absolute value of probability amplitudes of the wave functions of the nearly zero-energy eigenstates of the non-Hermitian SSH chain as a function of the sublattice $n$and the value of $ \upsilon $: (a) $\gamma = 0.4$; (b) $\gamma = 1.4$. The other parameters of the non-Hermitian SSH chain are chosen as $ w = 1.0 $and $ N = 20 $.
图 4 非厄米SSH链的本征态波函数在每个子格上的概率分布图 (a1) $ \upsilon = 0.01 $; (a2) $ \upsilon = - 0.01 $; (b1) $ \upsilon = 0.2 $; (b2) $ \upsilon = - 0.2 $; (c1) $ \upsilon = 0.4 $; (c2) $ \upsilon = - 0.4 $; (d1) $ \upsilon = 0.7 $; (d2) $ \upsilon = - 0.7 $; (e1) $ \upsilon = 1.5 $; (e2) $ \upsilon = - 1.5 $; 非厄米SSH链的其他参数选取为$\gamma = $$ 0.4$, $ w = 1.0 $, $ N = 20 $
Fig. 4. Distribution of probabilities of the wave functions of the non-Hermitian SSH chain: (a1) $ \upsilon = 0.01 $; (a2) $ \upsilon = - 0.01 $; (b1) $ \upsilon = 0.2 $; (b2) $ \upsilon = - 0.2 $; (c1) $ \upsilon = 0.4 $; (c2) $ \upsilon = - 0.4 $; (d1) $ \upsilon = 0.7 $; (d2) $ \upsilon = - 0.7 $; (e1) $ \upsilon = 1.5 $; (e2) $ \upsilon = - 1.5 $. The other parameters of the non-Hermitian SSH chain are chosen as $\gamma = 0.4$, $ w = 1.0 $ and $ N = 20 $.
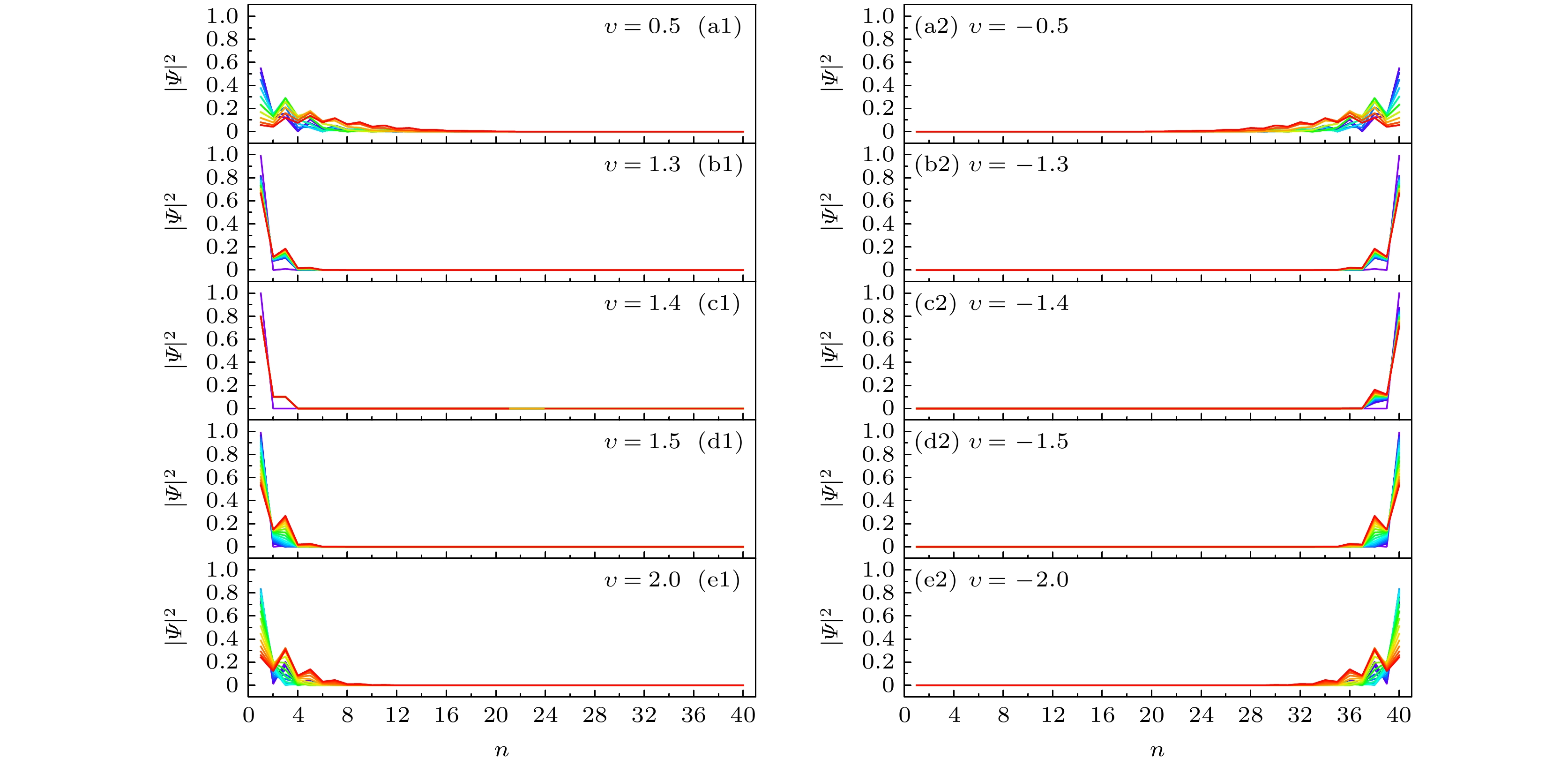
图 5 非厄米SSH链的本征态波函数在每个子格上的概率分布图 (a1) $ \upsilon = 0.5 $; (a2) $ \upsilon = - 0.5 $; (b1) $ \upsilon = 1.3 $; (b2) $ \upsilon = - 1.3 $; (c1) $ \upsilon = 1.4 $; (c2) $ \upsilon = - 1.4 $; (d1) $ \upsilon = 1.5 $; (d2) $ \upsilon = - 1.5 $; (e1) $ \upsilon = 2.0 $; (e2) $ \upsilon = - 2.0 $; 非厄米SSH链的其他参数选取为$\gamma = $$ 1.4$, $ w = 1.0 $, $ N = 20 $
Fig. 5. Distribution of probabilities of the wave functions of the non-Hermitian SSH chain: (a1) $ \upsilon = 0.5 $; (a2) $ \upsilon = - 0.5 $; (b1) $ \upsilon = 1.3 $; (b2) $ \upsilon = - 1.3 $; (c1) $ \upsilon = 1.4 $; (c2) $ \upsilon = - 1.4 $; (d1) $ \upsilon = 1.5 $; (d2) $ \upsilon = - 1.5 $; (e1) $ \upsilon = 2.0 $; (e2) $ \upsilon = - 2.0 $. The other parameters of the non-Hermitian SSH chain are chosen as $\gamma = 1.4$, $ w = 1.0 $ and $ N = 20 $.
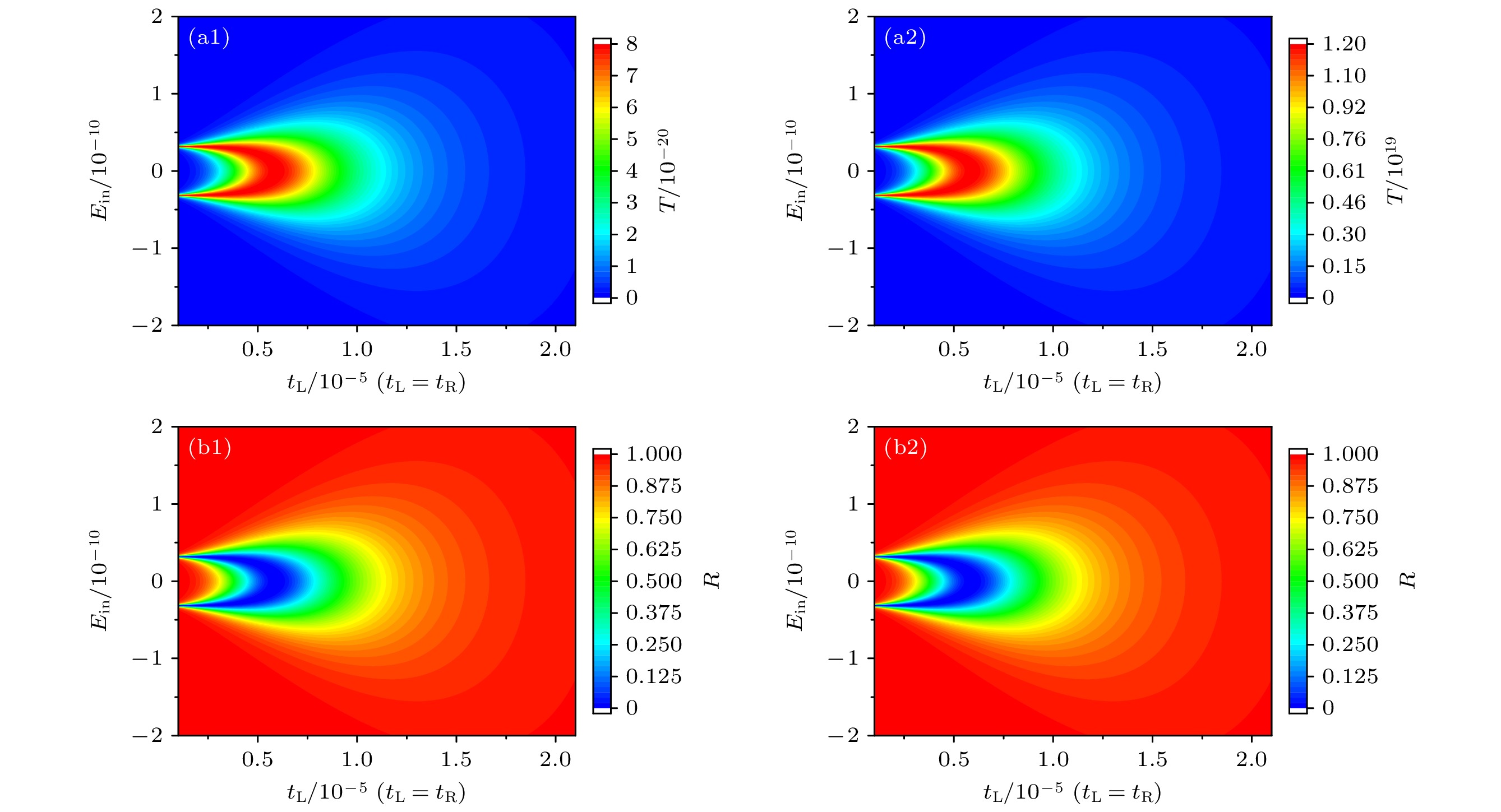
图 6 非厄米SSH链的电子透射率和反射率随不同隧穿耦合振幅和入射电子能量变化的相图 (a1), (b1) $ \upsilon = 0.5 $; (a2), (b2) $ \upsilon = $$ - 0.5 $; 非厄米SSH链的其他参数选取为$\gamma = 0.4$, $ w = 1.0 $, $ N = 20 $
Fig. 6. Transmission probabilities and reflection probabilities of the non-Hermitian SSH chain as a function of the amplitude of tunneling coupling and the energy of incident electron: (a1), (b1) $ \upsilon = 0.5 $; (a2), (b2) $ \upsilon = - 0.5 $. The other parameters of the non-Hermitian SSH chain are chosen as $\gamma = 0.4$, $ w = 1.0 $ and $ N = 20 $.
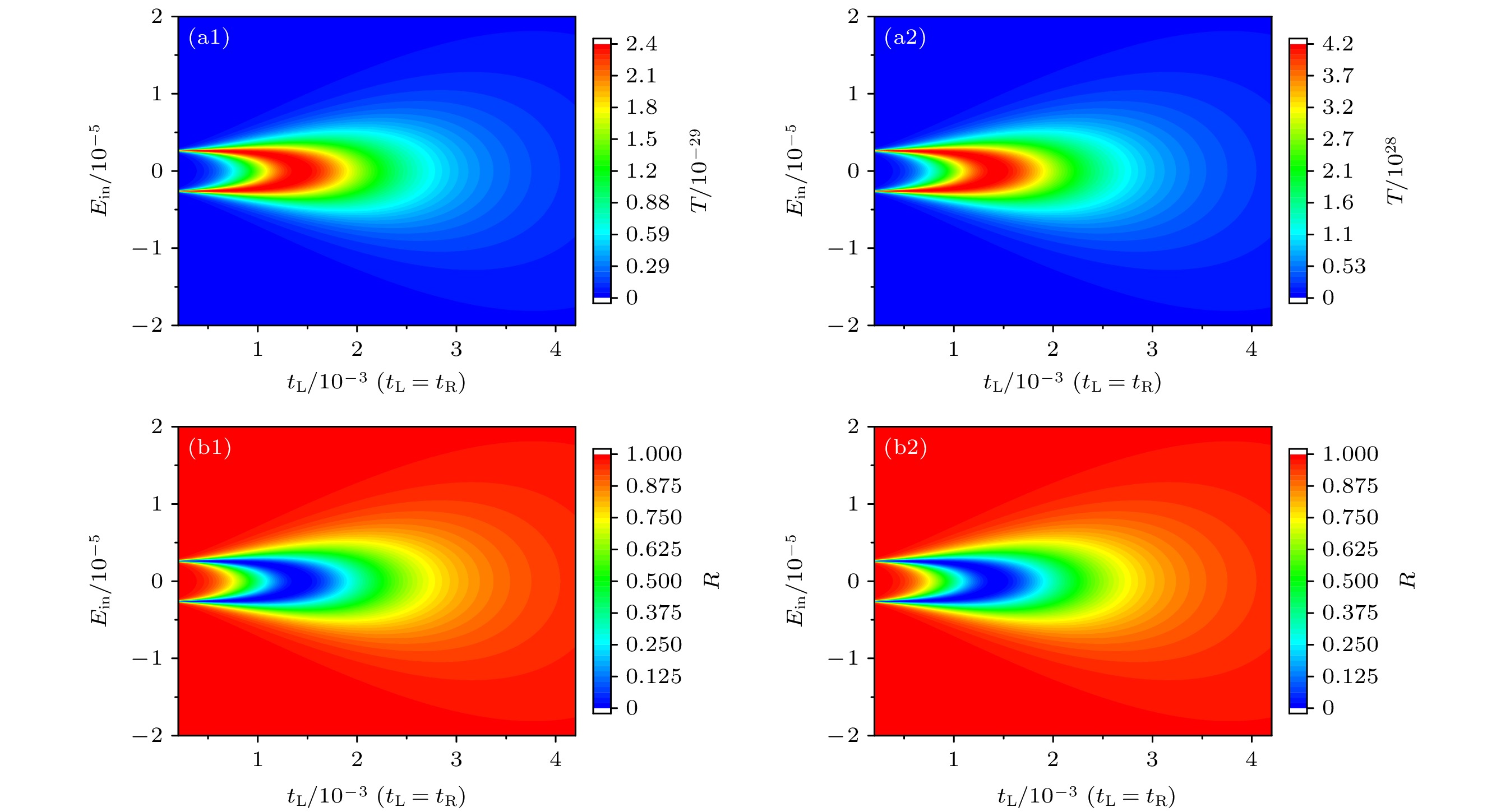
图 7 非厄米SSH链的电子透射率和反射率随不同隧穿耦合振幅和入射电子能量变化的相图 (a1), (b1) $ \upsilon = 1.3 $; (a2), (b2) $ \upsilon = $$ - 1.3 $; 非厄米SSH链的其他参数选取为$\gamma = 1.4$, $ w = 1.0 $, $ N = 20 $
Fig. 7. Transmission probabilities and reflection probabilities of the non-Hermitian SSH chain as a function of the amplitude of tunneling coupling and the energy of incident electron: (a1), (b1) $ \upsilon = 1.3 $; (a2), (b2) $ \upsilon = - 1.3 $. The other parameters of the non-Hermitian SSH chain are chosen as $\gamma = 1.4$, $ w = 1.0 $ and $ N = 20 $.
图 8 (a1), (b1)非厄米SSH链在零能级附近的能谱图; (a2), (b2)非厄米SSH链与左导线原子$ j = - 1 $和右导线原子$ j = 1 $耦合的修正系统在零能级附近的能谱图. 其中, (a1) $\gamma = 0.4$, (a2) $\gamma = 0.4$, $ {t_{\text{L}}} = {t_{\text{R}}} = 0.00002 $; (b1) $\gamma = 1.4$, (b2) $\gamma = 1.4$, $ {t_{\text{L}}} = $$ {t_{\text{R}}} = 0.004 $. 非厄米SSH链的其他参数选取为$ w = 1.0 $, $ N = 20 $.
Fig. 8. (a1), (b1) Real part of the energy spectrum of the non-Hermitian SSH chain in thevicinity of the zero energy; (a2), (b2) real part of the energy spectrum of the non-Hermitian SSH chain coupled to the first sublattice of the left lead $ j = - 1 $ and that of the right lead $ j = 1 $ in the vicinity of the zero energy. Here, (a1) $\gamma = 0.4$, (a2) $\gamma = 0.4$, $ {t_{\text{L}}} = {t_{\text{R}}} = 0.00002 $; (b1) $\gamma = 1.4$, (b2) $\gamma = $$ 1.4$, $ {t_{\text{L}}} = {t_{\text{R}}} = 0.004 $. The other parameters of the non-Hermitian SSH chain are chosen as $ w = 1.0 $ and $ N = 20 $.
-
[1] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
Google Scholar
[2] Bergholtz E J, Budich J C, K Flore K 2021 Rev. Mod. Phys. 93 015005
Google Scholar
[3] Zhang X, Zhang T, Lu M H, Chen Y F 2022 Adv. Phys. -X 7 2109431
Google Scholar
[4] Li A, Wei H, Cotrufo M, Chen W, Mann S, Ni X, Xu B, Chen J, Wang J, Fan S, Qiu CW, Alù A, Chen L 2023 Nat. Nanotechnol. 18 706
Google Scholar
[5] Banerjee A, Sarkar R, Dey S, Narayan A 2023 J. Phys. Condens. Matter 35 333001
Google Scholar
[6] Heiss W D 2012 J. Phys. A: Math. Theor. 45 444016
Google Scholar
[7] Mandal I, Bergholtz E J, 2021 Phys. Rev. Lett. 127 186601
Google Scholar
[8] Wang Q, Chong Y D 2023 J. Opt. Soc. Am. B 40 1443
Google Scholar
[9] Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, ThomaleR 2020 Nat. Phys. 16 747
Google Scholar
[10] Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761
Google Scholar
[11] Ghataka A, Brandenbourgera M, van Wezela J, Coulaisa C 2020 Proc. Natl. Acad. Sci. U. S. A. 117 29561
Google Scholar
[12] Lee T E 2016 Phys. Rev. Lett. 116 133903
Google Scholar
[13] Jin L, Song Z 2019 Phys. Rev. B 99 081103(R
Google Scholar
[14] Wang X R, Guo C X, Kou S P 2020 Phys. Rev. B 101 121116(R
Google Scholar
[15] Wang X R, Guo C X, Du Q, Kou S P 2020 Chin. Phys. Lett. 37 117303
Google Scholar
[16] Jezequel L, Delplace P 2023 Phys. Rev. Lett. 130 066601
Google Scholar
[17] Zeuner J M, Rechtsman M C, Plotnik Y, Lumer Y, Nolte S, Rudner M S, Segev M, SzameitA 2015 Phys. Rev. Lett. 115 040402
Google Scholar
[18] Weimann S, Kremer M, Plotnik Y, Lumer Y, Nolte S, Makris K G, Segev M, Rechtsman M C, Szameit A 2017 Nat. Mater. 16 433
Google Scholar
[19] Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311
Google Scholar
[20] Liu S, Shao R, Ma S, Zhang L, You O, Wu H, Xiang Y J, Cui T J, Zhang S 2021 Research 2021 5608038
Google Scholar
[21] Liang Q, Xie D, Dong Z, Li H, Li H, Gadway B, Yi W, Yan B 2022 Phys. Rev. Lett. 129 070401
Google Scholar
[22] Zhou Q, Wu J, Pu Z, Lu J, Huang X, Deng W, Ke M, Liu Z, 2023 Nat. Commun. 14 4569
Google Scholar
[23] Feng Y, Liu Z, Liu F, Yu J, Liang S, Li F, Zhang Y, Xiao M, Zhang Z 2023 Phys. Rev. Lett. 131 013802
Google Scholar
[24] Zhang H, Chen T, Li L, Lee C H, Zhang X 2023 Phys. Rev. B 107 085426
Google Scholar
[25] Lee C H, Thomale R 2019 Phys. Rev. B 99 201103(R
Google Scholar
[26] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801
Google Scholar
[27] Lin Z, Lin Y, Yi W 2022 Phys. Rev. B 106 063112
Google Scholar
[28] Zeng Q B 2022 Phys. Rev. B 106 235411
Google Scholar
[29] Li J R, Luo C, Zhang L L, Zhang S F, Zhu P P, Gong W J 2023 Phys. Rev. A 107 022222
Google Scholar
[30] Tang C, Yang H, Song L, Yao X, Yan P, Cao Y 2023 Phys. Rev. B 108 035410
Google Scholar
[31] Kokhanchik P, Solnyshkov D, MalpuechG 2023 Phys. Rev. B 108 L041403
Google Scholar
[32] Su W P, SchriefferJ R, HeegerA J 1980 Phys. Rev. B 22 2099
Google Scholar
[33] Li H, Yi W 2022 Phys. Rev. A 106 053311
Google Scholar
[34] 张蓝云, 薛海斌, 陈彬, 陈建宾, 邢丽丽 2020 69 077301
Google Scholar
Zhang L Y, Xue H B, Chen B, Chen J B, Xing L L 2020 Acta Phys. Sin. 69 077301
Google Scholar
[35] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽 2021 70 087301
Google Scholar
Xue H B, Duan Z L, Chen B, Chen J B, Xing L L 2021 Acta Phys. Sin. 70 087301
Google Scholar
[36] Ye C Z, Zhang L Y, Xue H B 2022 Chin. Phys. B 31 027304
Google Scholar
[37] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
下载:
计量
- 文章访问数: 2810
- PDF下载量: 235
- 被引次数: 0
