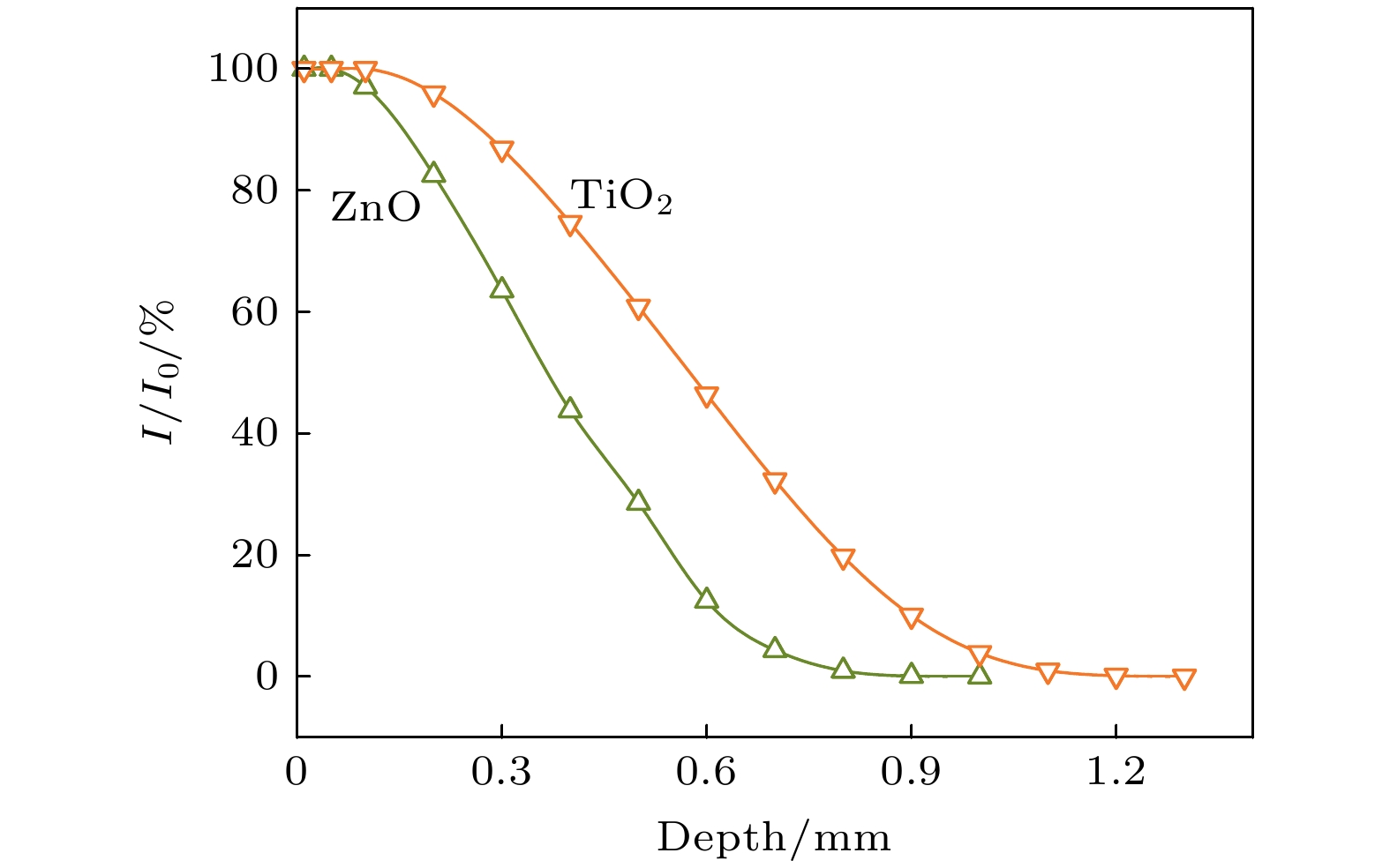
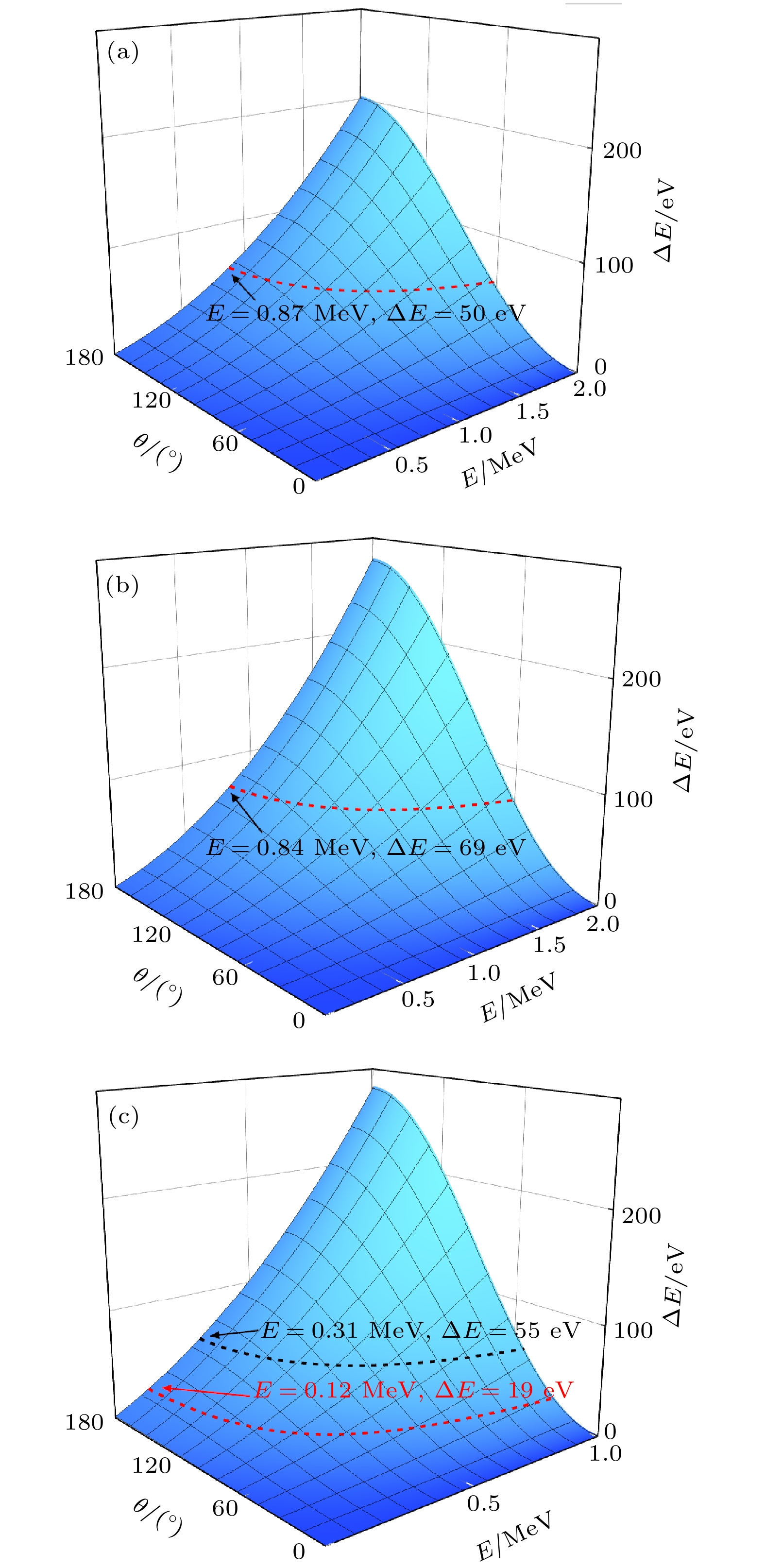
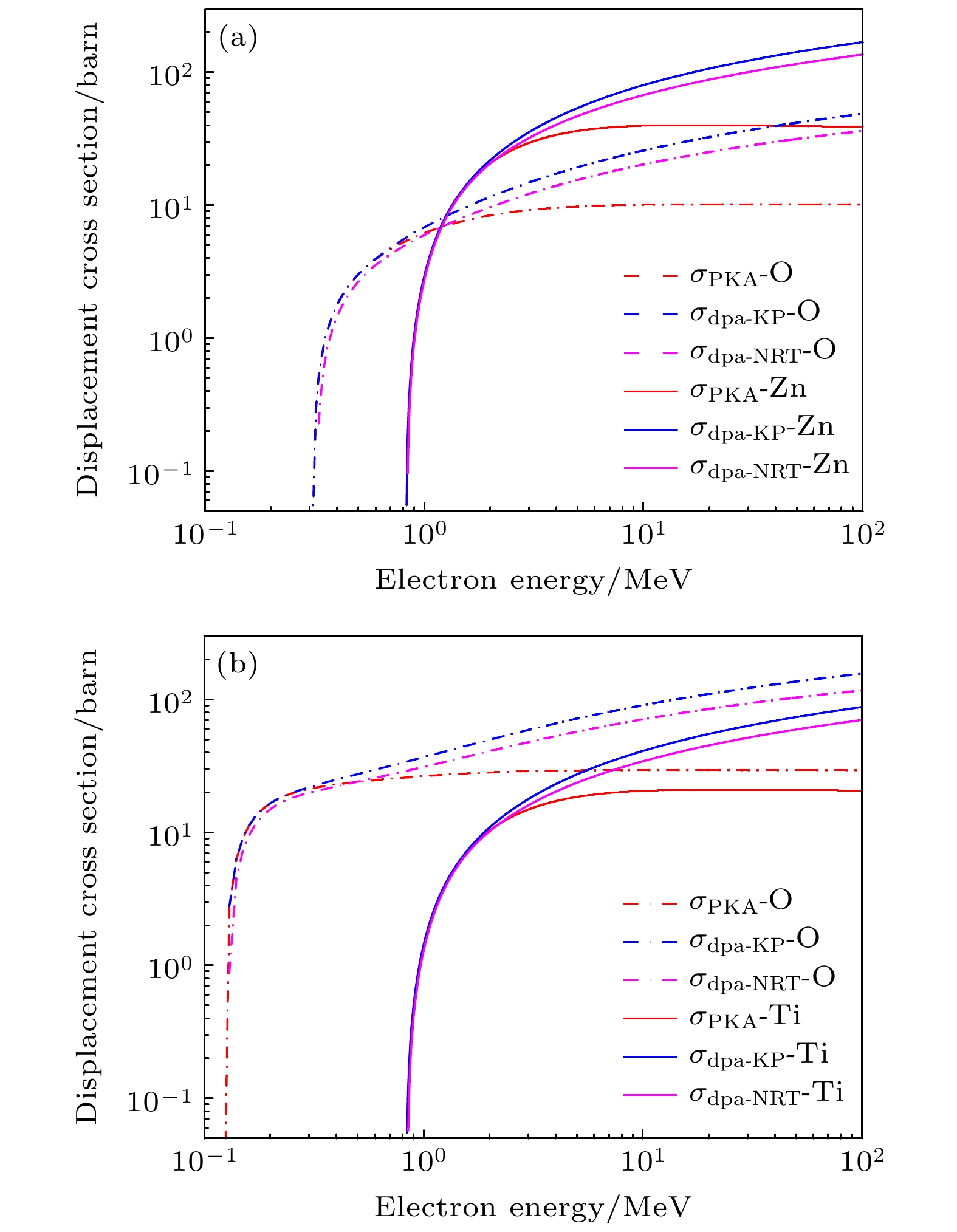
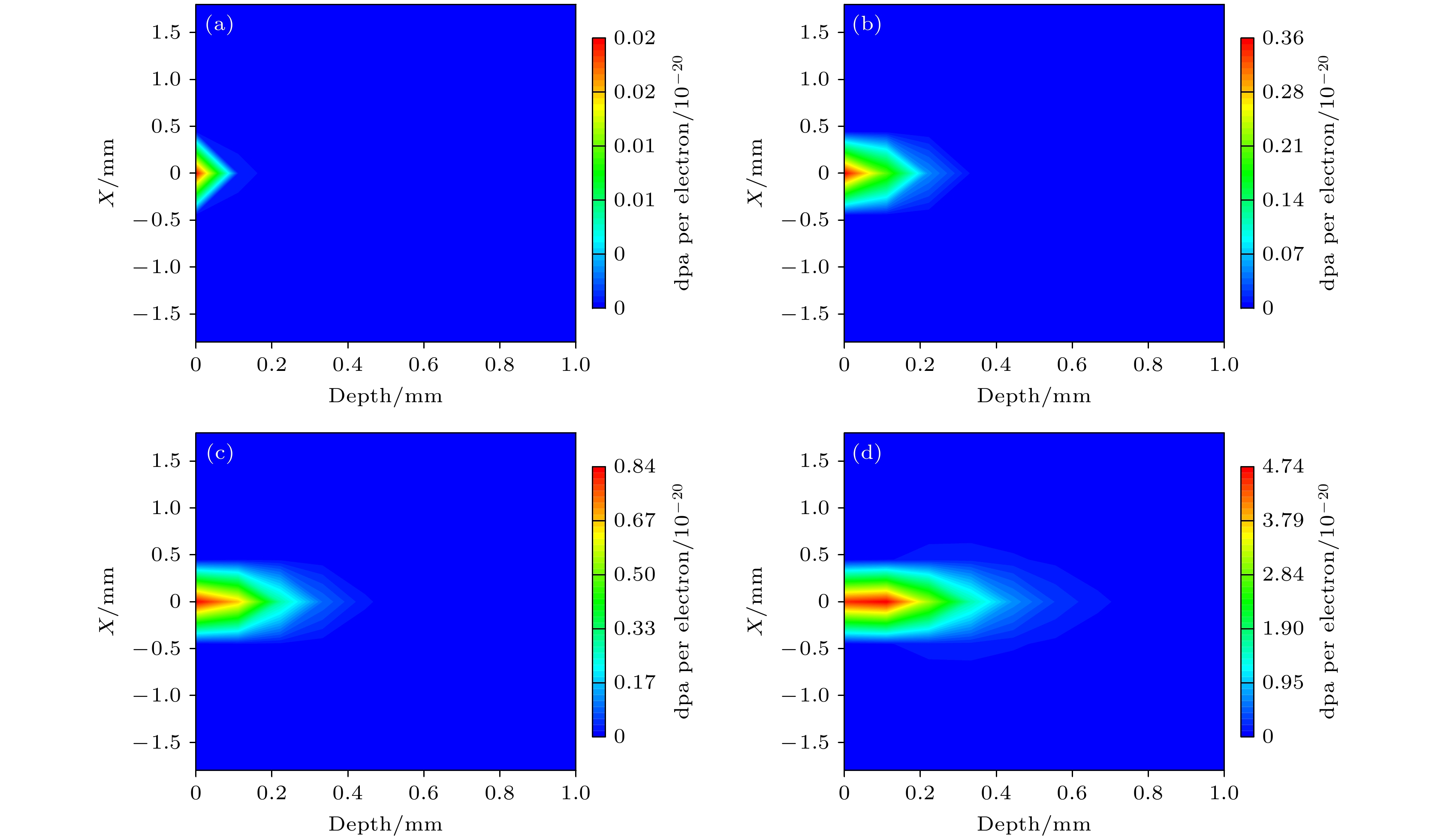
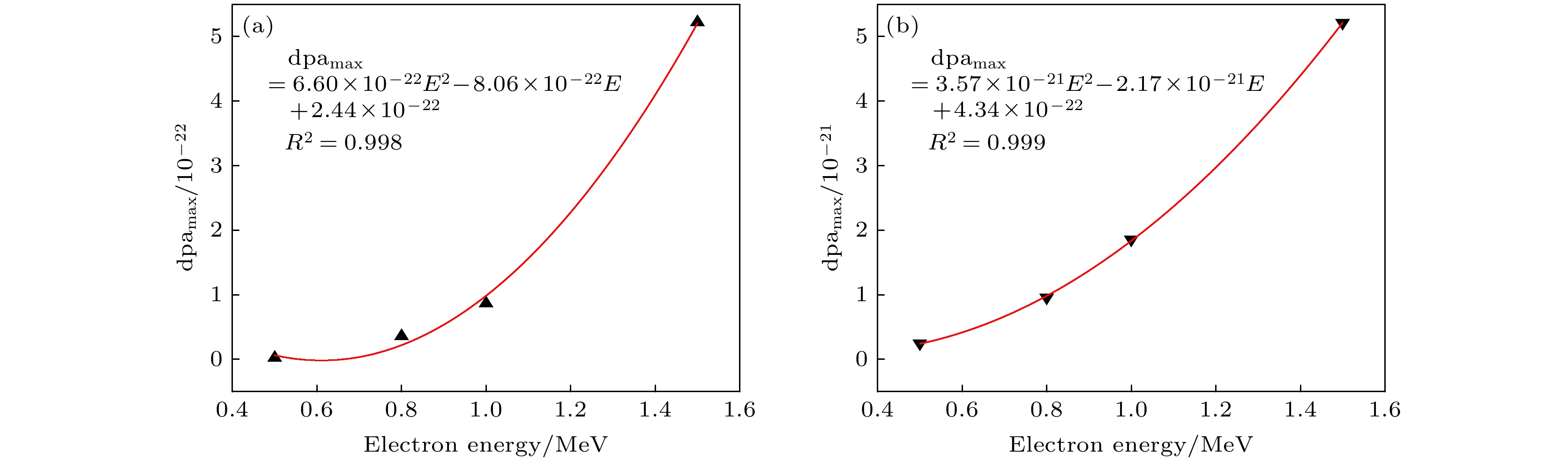
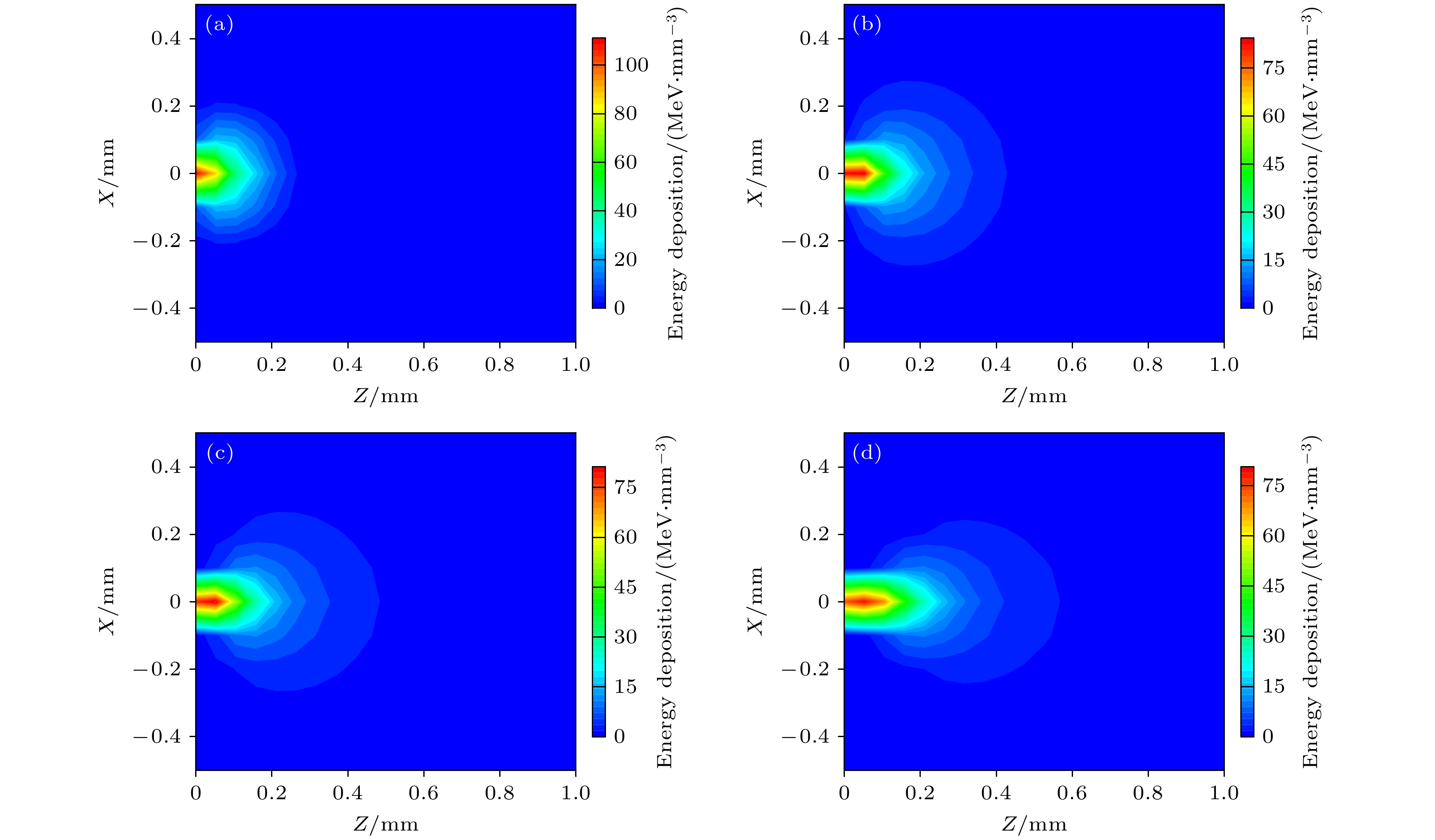
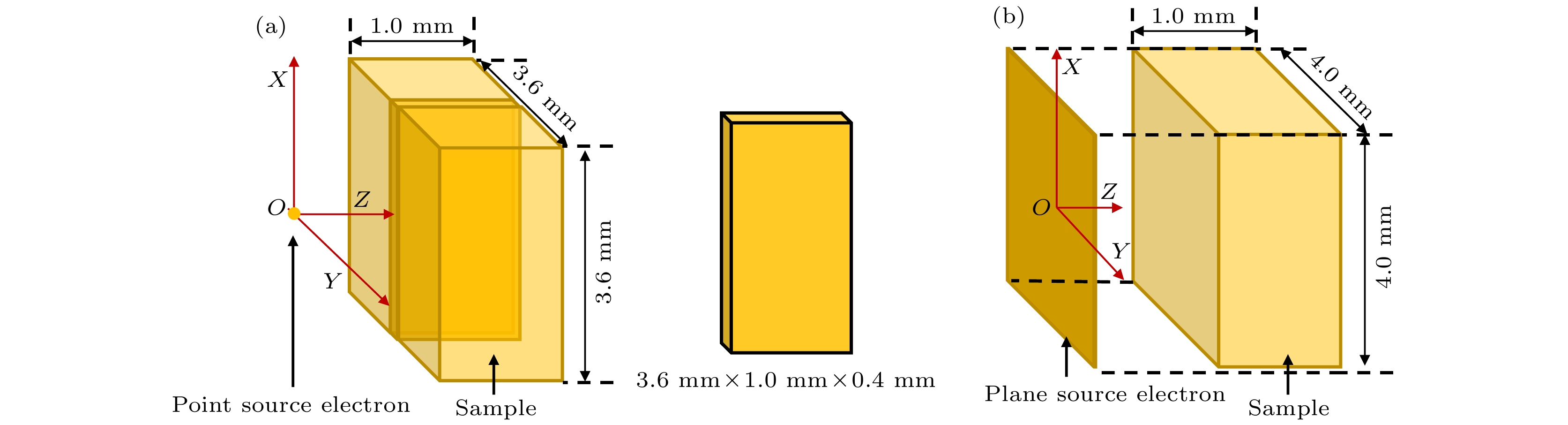
-
Wurtzite ZnO and rutile TiO2 have important application value in solar cells, photocatalysts, self-cleaning coatings, etc. In addition, ZnO and TiO2 are crucial basic materials for the development of semiconductor spintronics devices due to room temperature ferromagnetism in the state of defects or doped specific elements. Many studies indicate that the magnetic, optical, and electrical properties of ZnO and TiO2 are affected by intrinsic defects (such as vacancies, interstitial atoms, etc.). Electron irradiation has the incomparable advantages over other particle beam irradiation, the defects produced by electron beam irradiation are mainly independent vacancy-interstitial atom pairs (Frenkel pairs), and there are no new doping elements introduced into the material during the irradiation by electron beam with energy of several MeV, that is, electron irradiation is a relatively “pure” particle irradiation method. On the one hand, since the displacement threshold energy values of different atoms are different from each other, the type of defect during electron irradiation can be controlled by the energy of the electron beam. On the other hand, the electron fluence can determine the concentration of defects. Therefore, various defects of different concentrations can be generated by electron irradiation, thereby studying the influences of related defects on the magnetic, optical, and electrical properties of ZnO and TiO2. However, simulation calculations related to electron beam irradiation damage are relatively scarce. Therefore, in this work, the electron beam irradiation damage is taken as a research topic and the related theoretical simulation calculations are carried out, which lays a theoretical foundation for subsequent experimental researches. The size and the distribution of radiation damage (dpa) caused by point source electrons and that by plane source electrons with different energy values in ZnO and TiO2 are simulated and calculated through the MCNP5 program combined with the MCCM algorithm. The calculation results show that O atoms and Zn atoms can be dislocated when the electron energy values are greater than 0.31 MeV and 0.87 MeV in ZnO, respectively; while in TiO2, O atoms and Ti atoms can be dislocated when the electron beam energy values are greater than 0.12 MeV and 0.84 MeV, respectively. The dpa caused by point source electrons is mainly distributed in the longitudinal direction, and attenuates quickly in the lateral direction; on the contrary, the dpa caused by plane source electrons first increases and then decreases with the augment of the electron incidence depth, and the unevenness of the dpa distribution becomes more serious with the increase of the electron energy. Therefore, for each of ZnO and TiO2, the dpa will be relatively even distribution when the thickness of the sample is about 0.25 mm. Furthermore, the calculation results of the electron energy deposition show that the size of the energy deposition area is closely related to the electron beam energy. At the same time, with the increase of the electron beam energy, the position where the maximum energy deposition appears gradually moves to the inside of the sample, and the entire energy deposition area has a tendency to lean forward.
-
Keywords:
- electron irradiation /
- Monte Carlo assited classsical method algorithm /
- ZnO /
- TiO2
[1] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, von Molnár S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488
Google Scholar
[2] Furdyna J K 1988 J. Appl. Phys. 64 R29
Google Scholar
[3] Matsumoto Y, Takahashi R, Murakami M, Koida T, Fan X J, Hasegawa T, Fukumura T, Kawasaki M, Koshihara S Y, Koinuma H 2001 Jpn. J. Appl. Phys. 40 L1204
Google Scholar
[4] Xing G Z, Lu Y H, Tian Y F, Yi J B, Lim C C, Li Y F, Li G P, Wang D D, Yao B, Ding J, Feng Y P, Wu T 2011 AIP Advances 1 022152
Google Scholar
[5] Zhou S Q, Čižmár E, Potzger K, Krause M, Talut G, Helm M, Fassbender J, Zvyagin S A, Wosnitza J, Schmidt H 2009 Phys. Rev. B 79 113201
Google Scholar
[6] Duhalde S, Vignolo M F, Golmar F, Chiliotte C, Torres C E R, Errico L A, Cabrera A F, Rentería M, Sánchez F H, Weissmann M 2005 Phys. Rev. B 72 161313
Google Scholar
[7] Olayinka A S, Adetunji B I, Idiodi J O A, Aghemelon U 2019 Int. J. Mod. Phys. B 33 1950036
Google Scholar
[8] Kernazhitsky L, Shymanovska V, Gavrilko T, Naumov V, Fedorenko L, Kshnyakin V, Baran J 2014 J. Lumin. 146 199
Google Scholar
[9] Liu B J, Liu K, Zhao J W, Wang W H, Ralchenko V, Geng F J, Yang L, Zhang S, Xue J J, Han J C 2020 Diamond Relat. Mater. 109 108026
Google Scholar
[10] Fujishima A, Zhang X T 2006 C. R. Chim. 9 750
Google Scholar
[11] Lin Q L, Xu N N, Li G P, Qian Z F, Liu H, Wang R H 2021 J. Mater. Chem. C 9 2858
Google Scholar
[12] Liu H, Li G P, E D J, Xu N N, Lin Q L, Gao X D, Lan C, Chen J S, Wang C L, Zhan X W, Zhang K 2020 RSC Adv. 10 18687
Google Scholar
[13] Liu H, Li G P, E D J, Xu N N, Lin Q L, Gao X D, Wang C L 2020 Opt. Mater. 101 109748
Google Scholar
[14] Liu H, Li G P, E D J, Xu N N, Lin Q L, Gao X D, Wang C L 2020 J. Supercond. Nov. Magn. 33 1535
Google Scholar
[15] 张梅玲, 陈玉红, 张材荣, 李公平 2019 68 087101
Google Scholar
Zhang M L, Chen Y H, Zhang C R, Li G P 2019 Acta Phys. Sin. 68 087101
Google Scholar
[16] 林俏露, 李公平, 许楠楠, 刘欢, 王苍龙 2017 66 037101
Google Scholar
Lin Q L, Li G P, Xu N N, Liu H, Wang C L 2017 Acta Phys. Sin. 66 037101
Google Scholar
[17] 刘欢, 李公平, 许楠楠, 林俏露, 杨磊, 王苍龙 2016 65 206102
Google Scholar
Liu H, Li G P, Xu N N, Lin Q L, Yang L, Wang C L 2016 Acta Phys. Sin. 65 206102
Google Scholar
[18] 李天晶, 李公平, 马公俊平, 高行新 2011 60 116102
Google Scholar
Li T J, Li G P, Ma J P, Gao X X 2011 Acta Phys. Sin. 60 116102
Google Scholar
[19] Xu N N, Li G P, Pan X D, Wang Y B, Chen J S, Bao L M 2014 Chin. Phys. B 23 106101
Google Scholar
[20] Piñera I, Cruz C M, Van Espen P, Abreu Y, Leyva A 2012 Nucl. Instrum. Methods Phys. Res. , Sec. B 274 191
Google Scholar
[21] Cruz C M, Piñera I, Correa C, Abreu Y, Leyva A 2011 IEEE Nuclear Science Symposium Conference Record Valencia, Spain, 2011 p4622
[22] Nordlund K, Zinkle S J, Sand A E, Granberg F, Averback R S, Stoller R, Suzudo T, Malerba L, Banhart F, Weber W J 2018 Nat. Commun. 9 1
Google Scholar
[23] Edmondson P D, Weber W J, Namavar F, Zhang Y W 2012 J. Nucl. Mater. 422 86
Google Scholar
[24] Piñera I, Cruz C M, Abreu Y, Leyva A 2007 Phys. Status Solidi A 204 2279
Google Scholar
[25] Pinera I, Abreu Y, Van Espen P, Díaz A, Leyva A, Cruz C M 2011 IEEE Nuclear Science Symposium Conference Record Valencia, Spain, 2011 p1609
[26] Oen O S, Holmes D K 1959 J. Appl. Phys. 30 1289
Google Scholar
[27] Cahn J H 1959 J. Appl. Phys. 30 1310
Google Scholar
[28] Bethe H A, Ashkin J 1953 Experimental Nuclear Physics (Vol. 1) (London: John Wiley & Sons, Iinc., New York Champan & Hall, Limited) pp252-256
[29] Norgett M J, Robinson M T, Torrens I M 1975 Nucl. Eng. Des. 33 50
Google Scholar
[30] Nordlund K, Zinkle S J, Sand A E, Granberg F, Averback R S, Stoller R E, Suzudo T, Malerba L, Banhart F, Weber W J 2018 J. Nucl. Mater. 512 450
Google Scholar
[31] Kinchin G H, Pease R S 1955 J. Nucl. Energy (1954) 1 200
Google Scholar
[32] McKinley W A, Feshbach H 1948 Phys. Rev. 74 1759
Google Scholar
[33] Meese J M, Locker D R 1972 Solid State Commun. 11 1547
Google Scholar
[34] Zinkle S J, Kinoshita C 1997 J. Nucl. Mater. 251 200
Google Scholar
[35] Smith K L, Colella M 2003 J. Nucl. Mater. 321 19
Google Scholar
[36] Robinson M, Marks N A, Whittle K R, Lumpkin G R 2012 Phys. Rev. B 85 104105
Google Scholar
[37] Piñera I, Cruz C M, Leyva A, Abreu Y, Cabal A E, Van Espen P, Van Remortel N 2014 Nucl. Instrum. Methods Phys. Res. , Sec. B 339 1
Google Scholar
-
图 1 MCNP5采用程序模拟几何结构图 (a) 点源电子束; (b) 面源电子束
Figure 1. Schematic diagram of the geometry structure used by MCNP5 program: (a) Point source electron; (b) plane source electron.
图 2 1.0 MeV的电子束在纤锌矿ZnO及金红石TiO2样品中的吸收曲线
Figure 2. Absorption curve of 1.0 MeV electron beam in wurtzite ZnO and rutile TiO2 sample.
图 3 相对论性电子与静止原子的能量传递 (a) 64Zn; (b) 48Ti; (c) 16O
Figure 3. Energy transfer between relativistic electron and stationary atom: (a) 64Zn; (b) 48Ti; (c) 16O.
图 4 离位损伤截面 (a) wurtzite ZnO; (b) rutile TiO2
Figure 4. Displacement cross section: (a) wurtzite ZnO; (b) rutile TiO2.
图 5 点源电子束在纤锌矿ZnO中产生的dpa的分布 (a) 0.5 MeV; (b) 0.8 MeV; (c) 1.0 MeV; (d) 1.5 MeV
Figure 5. Distribution of dpa produced by Point Source Electron in wurtzite ZnO: (a) 0.5 MeV; (b) 0.8 MeV; (c) 1.0 MeV; (d) 1.5 MeV.
图 6 1.0 MeV电子辐照金红石TiO2时dpa的分布
Figure 6. Distribution of dpa produced by 1.0 MeV electron in rutile TiO2.
图 7 dpa随电子入射深度的变化曲线 (a) Wurtzite ZnO; (b) rutile TiO2
Figure 7. The variation curve of dpa with electron incidence depth: (a) Wurtzite ZnO; (b) rutile TiO2.
图 8 dpamax与电子能量的关系曲线 (a) Wurtzite ZnO; (b) rutile TiO2
Figure 8. Relationship between dpamax and electron energy: (a) Wurtzite ZnO; (b) rutile TiO2.
图 9 不同能量的理想点入射电子在纤锌矿ZnO中的能量沉积的分布
Figure 9. Distribution of energy deposition of ideal point source electrons with different energies in wurtzite ZnO.
图 10 不同能量的面源电子束在纤锌矿ZnO中的能量沉积的分布
Figure 10. Distribution of energy deposition of plane source electrons with different energies in wurtzite ZnO.
表 1 纤锌矿ZnO及金红石TiO2材料的平均激发势和离位阈能
Table 1. Average excitation potential and threshold energy of wurtzite ZnO and rutile TiO2.
DownLoad: CSV
-
[1] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, von Molnár S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488
Google Scholar
[2] Furdyna J K 1988 J. Appl. Phys. 64 R29
Google Scholar
[3] Matsumoto Y, Takahashi R, Murakami M, Koida T, Fan X J, Hasegawa T, Fukumura T, Kawasaki M, Koshihara S Y, Koinuma H 2001 Jpn. J. Appl. Phys. 40 L1204
Google Scholar
[4] Xing G Z, Lu Y H, Tian Y F, Yi J B, Lim C C, Li Y F, Li G P, Wang D D, Yao B, Ding J, Feng Y P, Wu T 2011 AIP Advances 1 022152
Google Scholar
[5] Zhou S Q, Čižmár E, Potzger K, Krause M, Talut G, Helm M, Fassbender J, Zvyagin S A, Wosnitza J, Schmidt H 2009 Phys. Rev. B 79 113201
Google Scholar
[6] Duhalde S, Vignolo M F, Golmar F, Chiliotte C, Torres C E R, Errico L A, Cabrera A F, Rentería M, Sánchez F H, Weissmann M 2005 Phys. Rev. B 72 161313
Google Scholar
[7] Olayinka A S, Adetunji B I, Idiodi J O A, Aghemelon U 2019 Int. J. Mod. Phys. B 33 1950036
Google Scholar
[8] Kernazhitsky L, Shymanovska V, Gavrilko T, Naumov V, Fedorenko L, Kshnyakin V, Baran J 2014 J. Lumin. 146 199
Google Scholar
[9] Liu B J, Liu K, Zhao J W, Wang W H, Ralchenko V, Geng F J, Yang L, Zhang S, Xue J J, Han J C 2020 Diamond Relat. Mater. 109 108026
Google Scholar
[10] Fujishima A, Zhang X T 2006 C. R. Chim. 9 750
Google Scholar
[11] Lin Q L, Xu N N, Li G P, Qian Z F, Liu H, Wang R H 2021 J. Mater. Chem. C 9 2858
Google Scholar
[12] Liu H, Li G P, E D J, Xu N N, Lin Q L, Gao X D, Lan C, Chen J S, Wang C L, Zhan X W, Zhang K 2020 RSC Adv. 10 18687
Google Scholar
[13] Liu H, Li G P, E D J, Xu N N, Lin Q L, Gao X D, Wang C L 2020 Opt. Mater. 101 109748
Google Scholar
[14] Liu H, Li G P, E D J, Xu N N, Lin Q L, Gao X D, Wang C L 2020 J. Supercond. Nov. Magn. 33 1535
Google Scholar
[15] 张梅玲, 陈玉红, 张材荣, 李公平 2019 68 087101
Google Scholar
Zhang M L, Chen Y H, Zhang C R, Li G P 2019 Acta Phys. Sin. 68 087101
Google Scholar
[16] 林俏露, 李公平, 许楠楠, 刘欢, 王苍龙 2017 66 037101
Google Scholar
Lin Q L, Li G P, Xu N N, Liu H, Wang C L 2017 Acta Phys. Sin. 66 037101
Google Scholar
[17] 刘欢, 李公平, 许楠楠, 林俏露, 杨磊, 王苍龙 2016 65 206102
Google Scholar
Liu H, Li G P, Xu N N, Lin Q L, Yang L, Wang C L 2016 Acta Phys. Sin. 65 206102
Google Scholar
[18] 李天晶, 李公平, 马公俊平, 高行新 2011 60 116102
Google Scholar
Li T J, Li G P, Ma J P, Gao X X 2011 Acta Phys. Sin. 60 116102
Google Scholar
[19] Xu N N, Li G P, Pan X D, Wang Y B, Chen J S, Bao L M 2014 Chin. Phys. B 23 106101
Google Scholar
[20] Piñera I, Cruz C M, Van Espen P, Abreu Y, Leyva A 2012 Nucl. Instrum. Methods Phys. Res. , Sec. B 274 191
Google Scholar
[21] Cruz C M, Piñera I, Correa C, Abreu Y, Leyva A 2011 IEEE Nuclear Science Symposium Conference Record Valencia, Spain, 2011 p4622
[22] Nordlund K, Zinkle S J, Sand A E, Granberg F, Averback R S, Stoller R, Suzudo T, Malerba L, Banhart F, Weber W J 2018 Nat. Commun. 9 1
Google Scholar
[23] Edmondson P D, Weber W J, Namavar F, Zhang Y W 2012 J. Nucl. Mater. 422 86
Google Scholar
[24] Piñera I, Cruz C M, Abreu Y, Leyva A 2007 Phys. Status Solidi A 204 2279
Google Scholar
[25] Pinera I, Abreu Y, Van Espen P, Díaz A, Leyva A, Cruz C M 2011 IEEE Nuclear Science Symposium Conference Record Valencia, Spain, 2011 p1609
[26] Oen O S, Holmes D K 1959 J. Appl. Phys. 30 1289
Google Scholar
[27] Cahn J H 1959 J. Appl. Phys. 30 1310
Google Scholar
[28] Bethe H A, Ashkin J 1953 Experimental Nuclear Physics (Vol. 1) (London: John Wiley & Sons, Iinc., New York Champan & Hall, Limited) pp252-256
[29] Norgett M J, Robinson M T, Torrens I M 1975 Nucl. Eng. Des. 33 50
Google Scholar
[30] Nordlund K, Zinkle S J, Sand A E, Granberg F, Averback R S, Stoller R E, Suzudo T, Malerba L, Banhart F, Weber W J 2018 J. Nucl. Mater. 512 450
Google Scholar
[31] Kinchin G H, Pease R S 1955 J. Nucl. Energy (1954) 1 200
Google Scholar
[32] McKinley W A, Feshbach H 1948 Phys. Rev. 74 1759
Google Scholar
[33] Meese J M, Locker D R 1972 Solid State Commun. 11 1547
Google Scholar
[34] Zinkle S J, Kinoshita C 1997 J. Nucl. Mater. 251 200
Google Scholar
[35] Smith K L, Colella M 2003 J. Nucl. Mater. 321 19
Google Scholar
[36] Robinson M, Marks N A, Whittle K R, Lumpkin G R 2012 Phys. Rev. B 85 104105
Google Scholar
[37] Piñera I, Cruz C M, Leyva A, Abreu Y, Cabal A E, Van Espen P, Van Remortel N 2014 Nucl. Instrum. Methods Phys. Res. , Sec. B 339 1
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6443
- PDF Downloads: 252
- Cited By: 0
