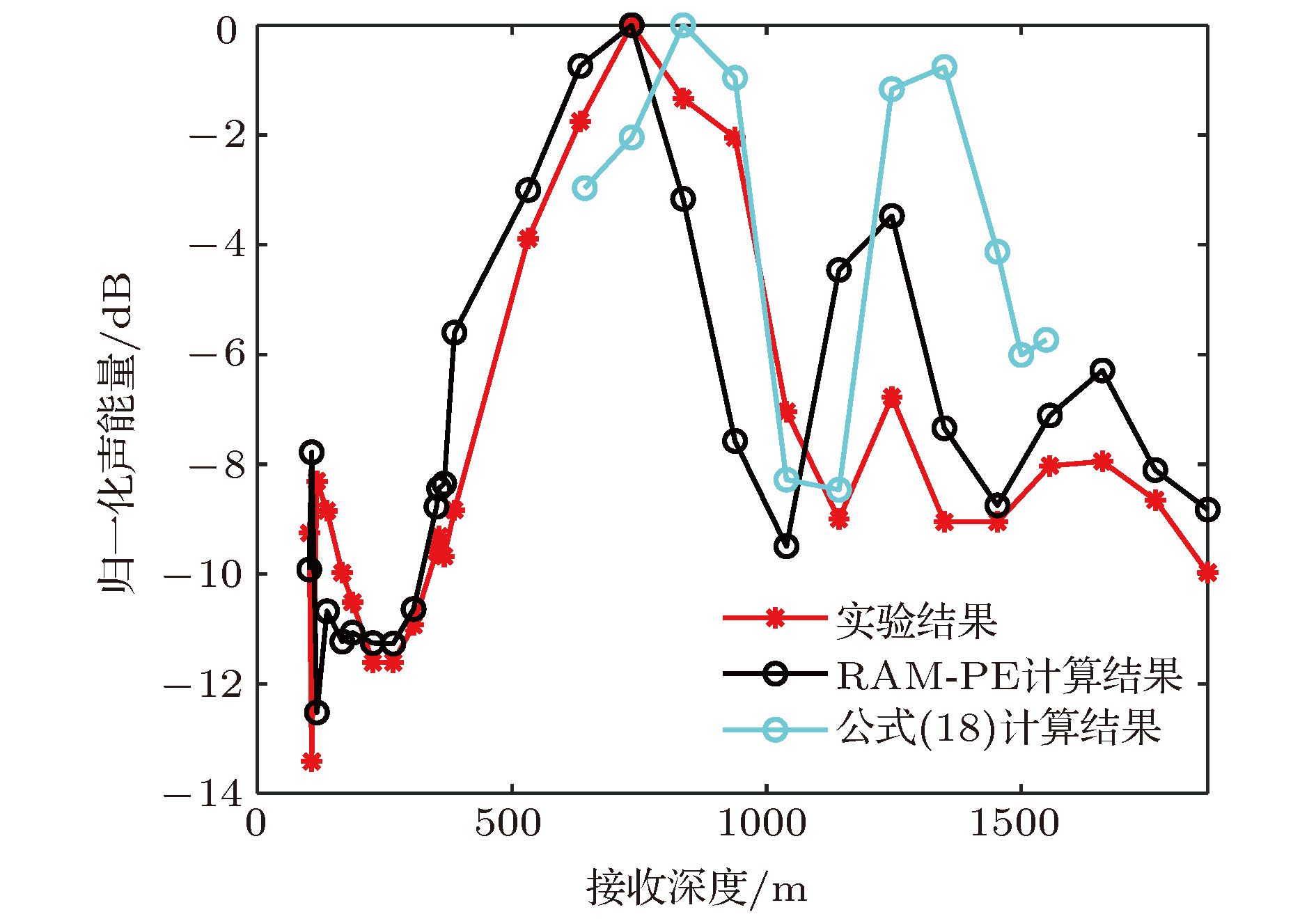
-
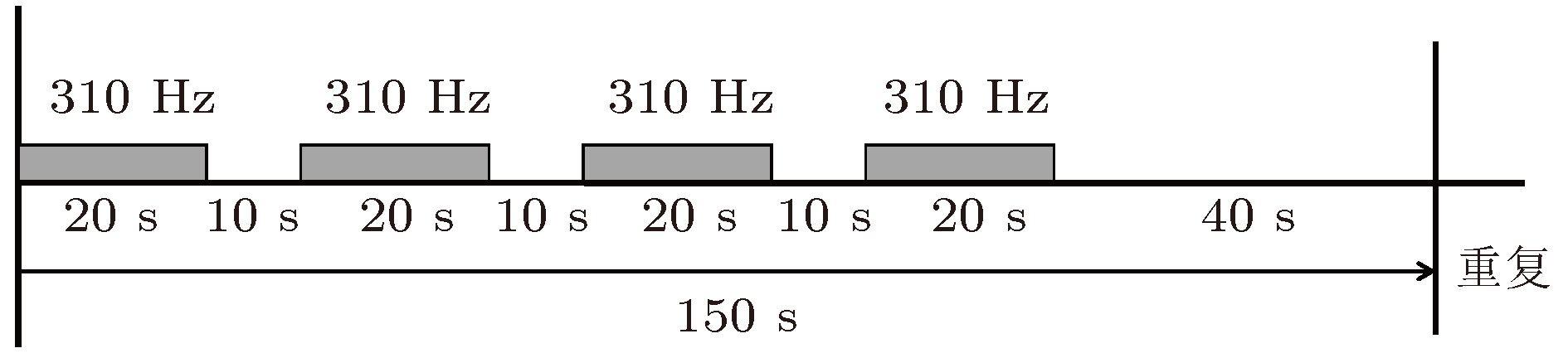
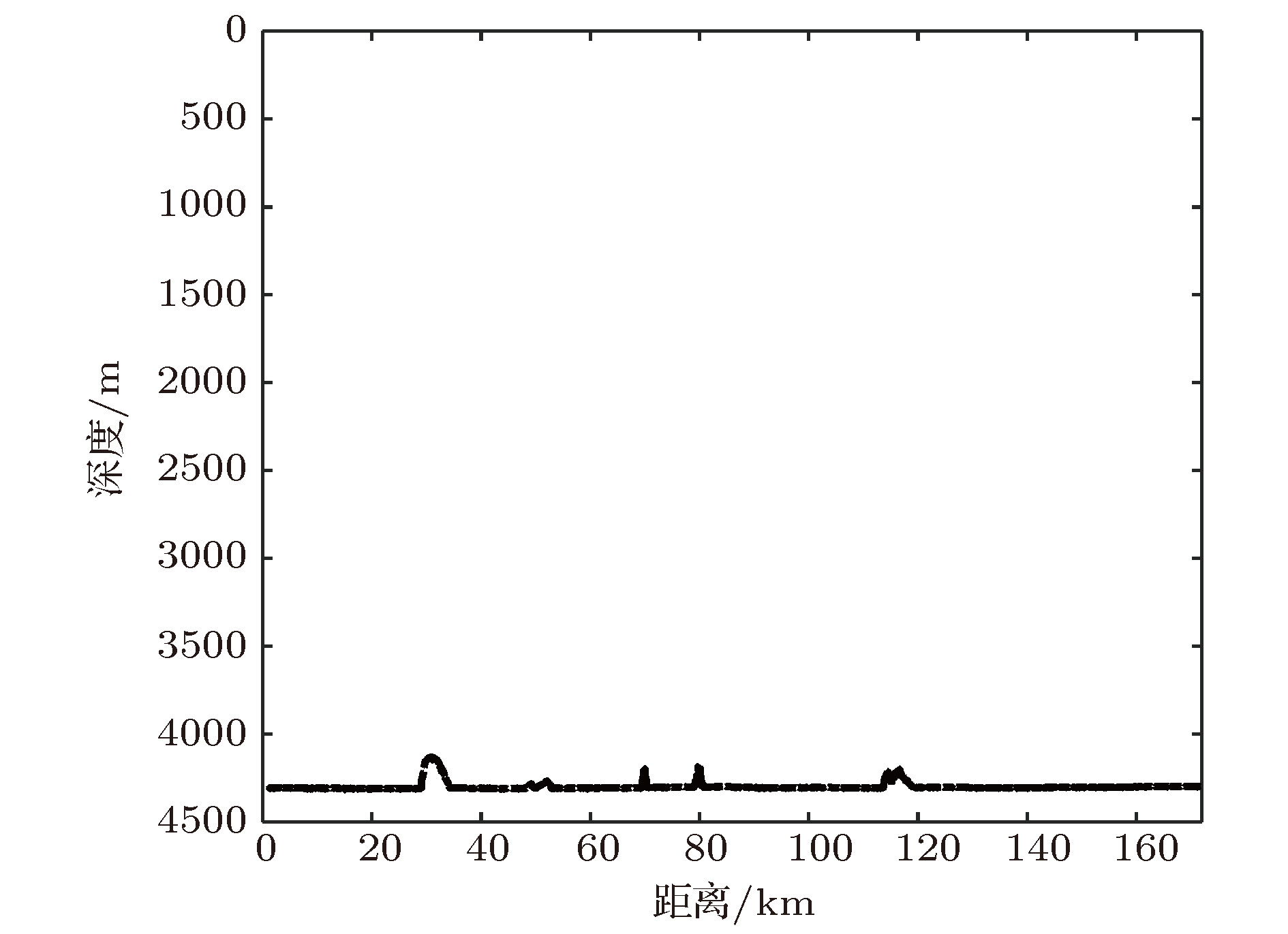
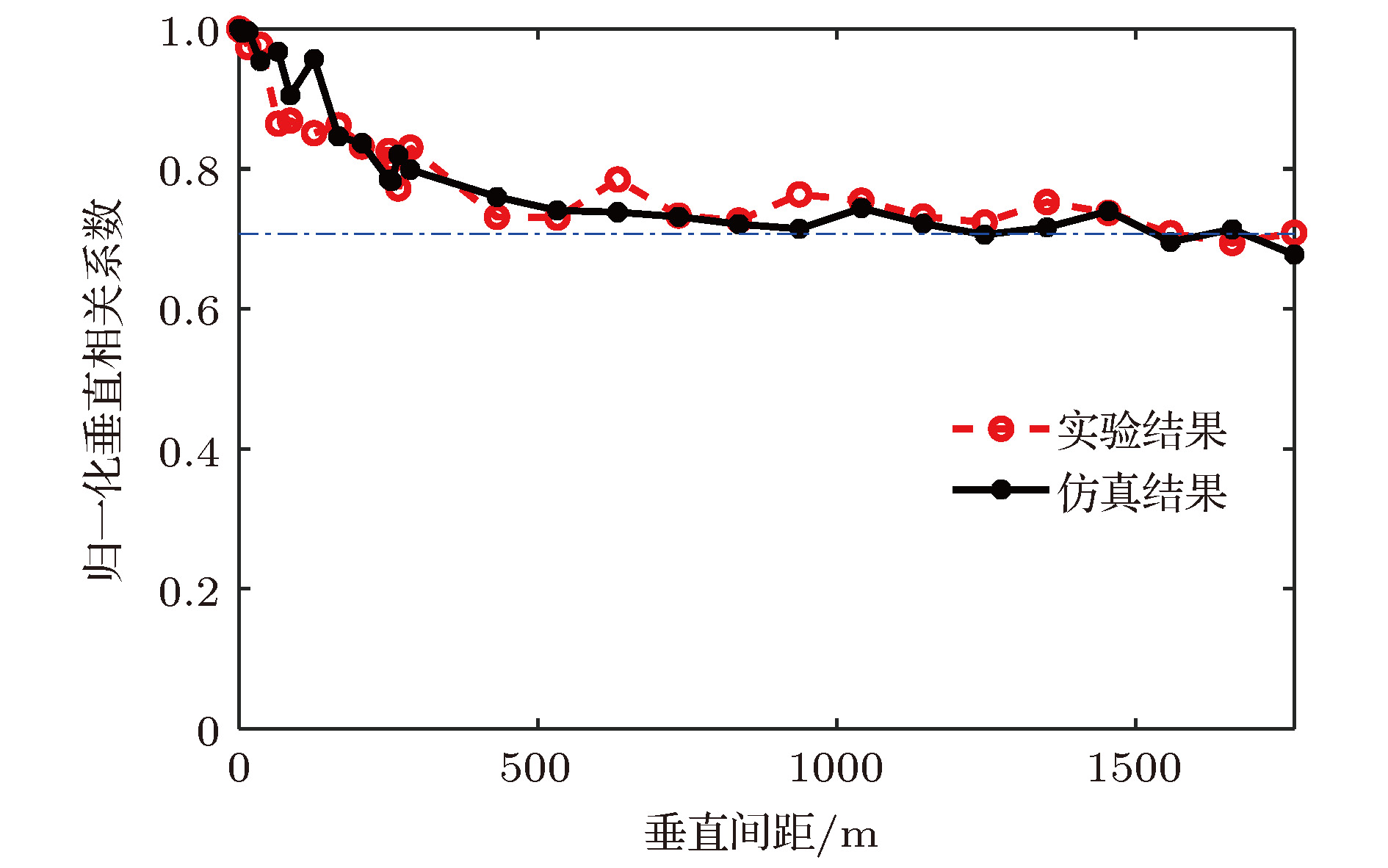
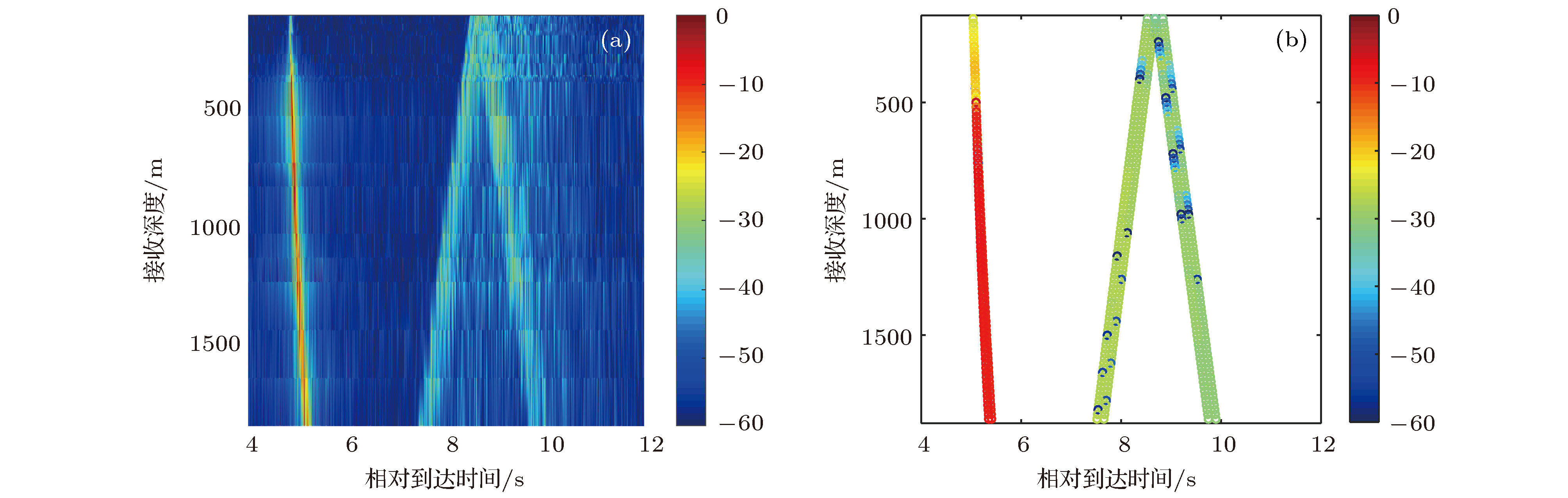
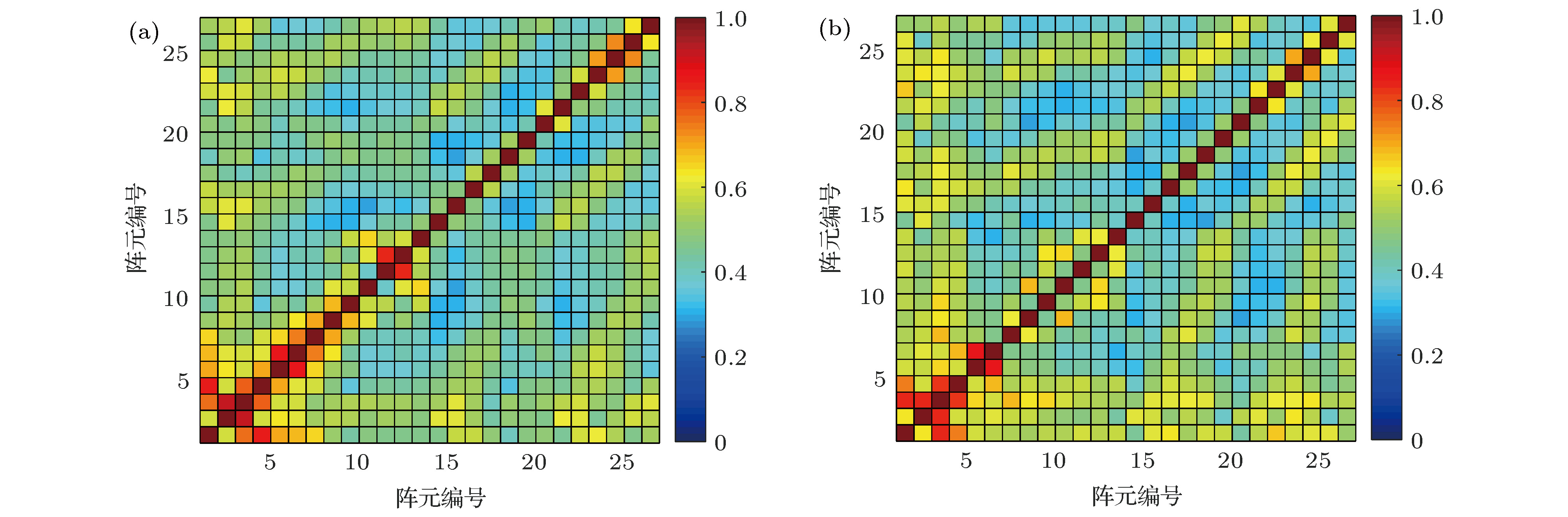
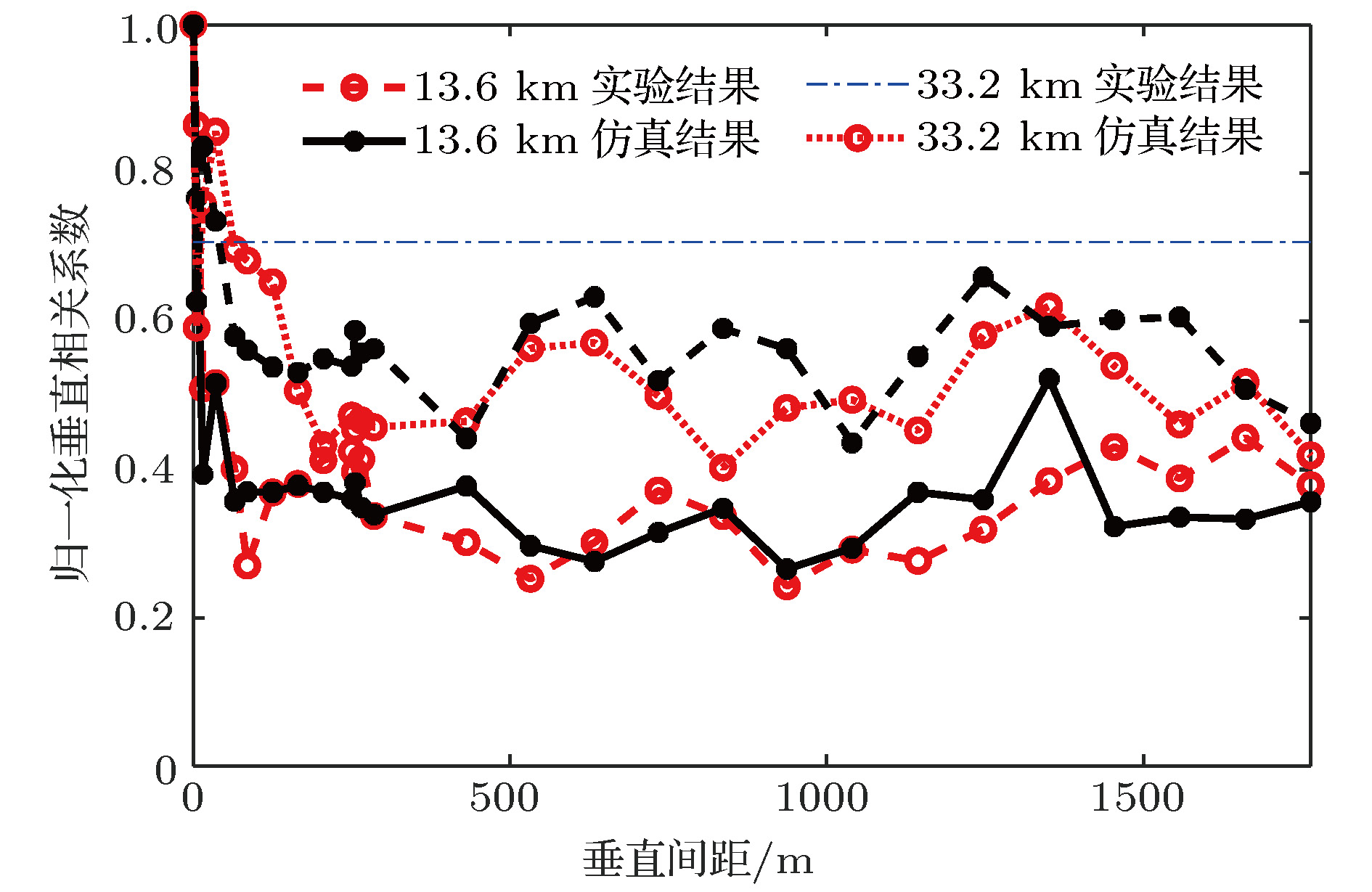
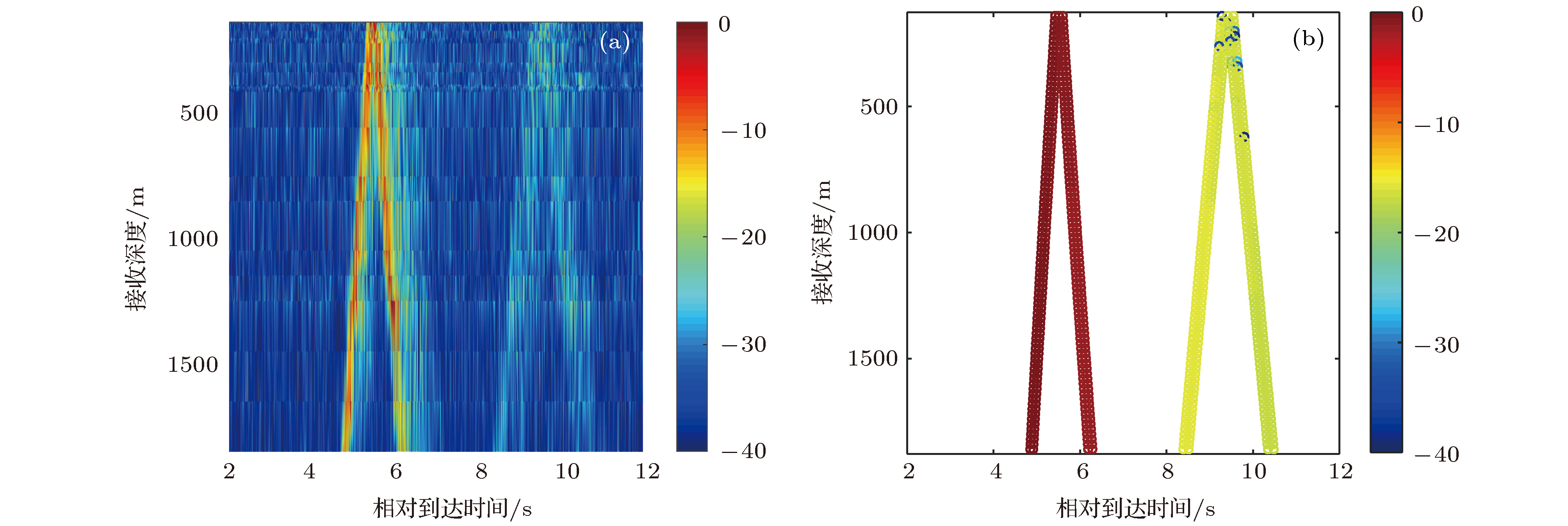
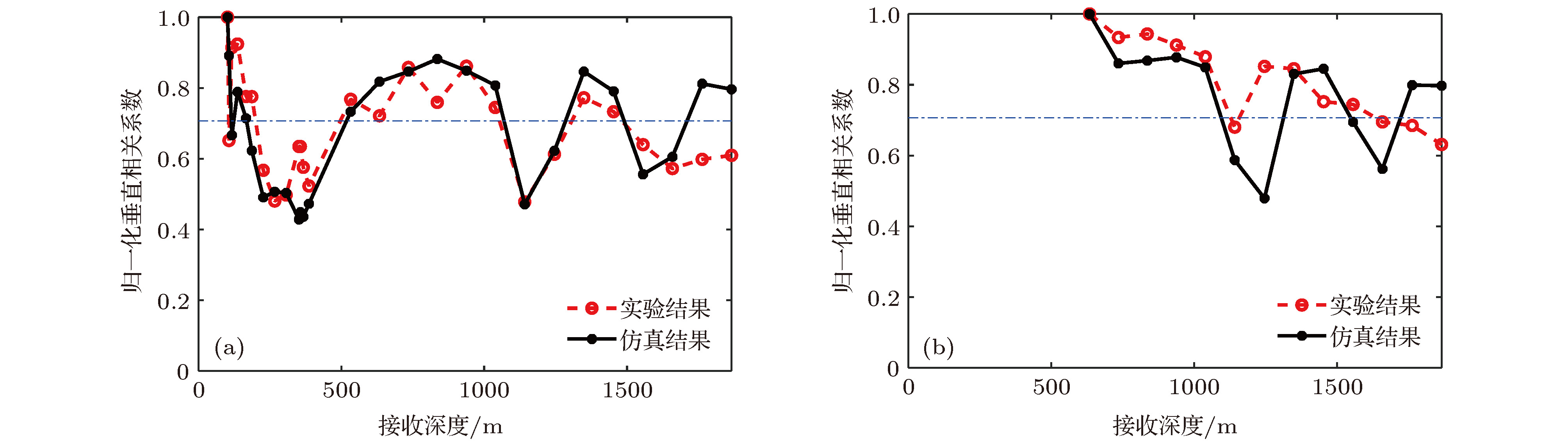
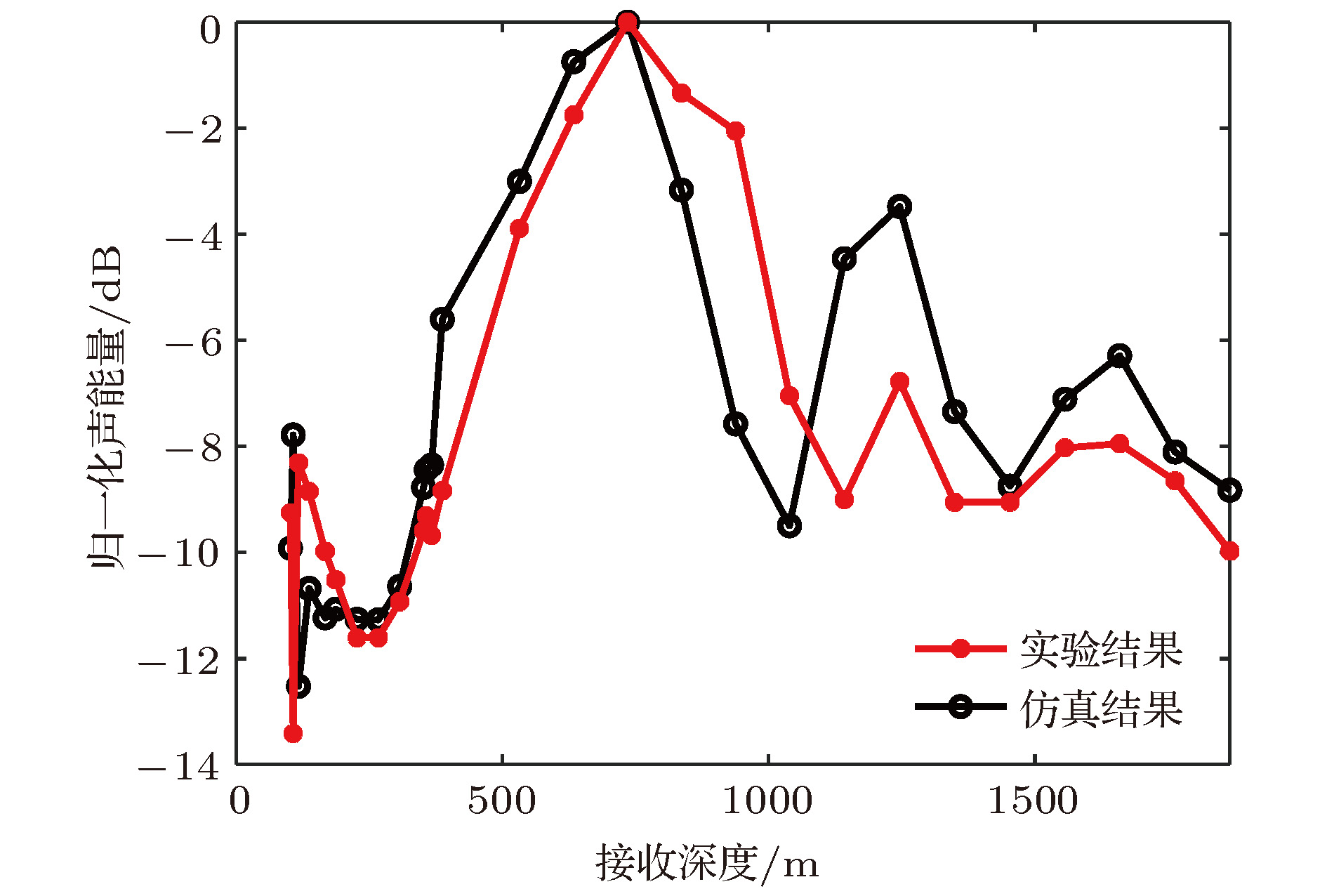
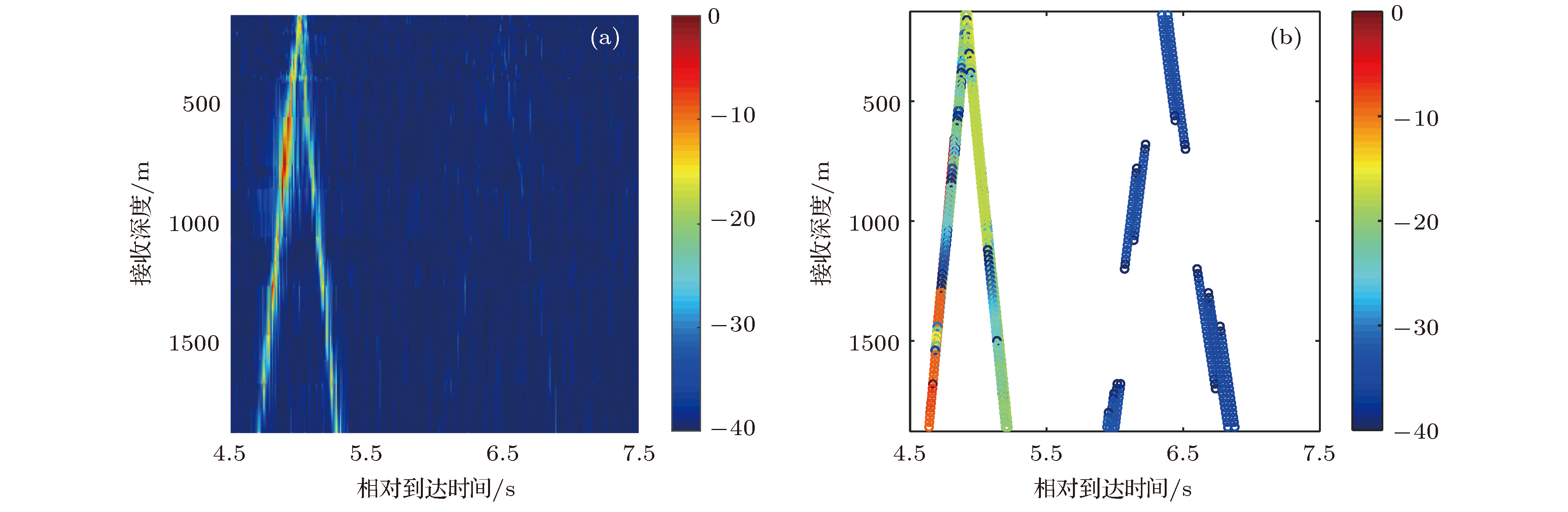
The research on the vertical correlation characteristics of sound field in deep water has important implications for enhancing the vertical array gain and improving the ability to detect the underwater target. Based on a deep-water experiment conducted in the South China Sea, the vertical coherence of sound fields in the direct zone, shadow zone and convergence zone are analyzed with the sound signals received by a vertical line array that covers the maximal depth to 1,866 m. The numerical analysis based on the ray theory is carried out to provide corresponding theoretical explanations to the variations of the vertical correlation characteristics at different ranges and depths. The vertical correlation coefficients in the direct zone are higher than 0.707 for the whole depth and drop very little with the increase of the vertical depth. It is because the main contributions come from direct arrival ray and sea surface reflection ray. The pulse structure is relatively simple, and the time delays of the two rays increase with the space between two receivers increasing. In the shadow zone, sound energy mainly comes from bottom reflection. Therefore, the vertical correlation coefficients are relatively low. Multi-path arrival is observed obviously. Vertical correlation coefficients drop quickly with depth increasing. With range increasing, the time delays of the multi-path pulses decrease. The vertical correlation coefficients at the same depth will increase a little with range increasing. Near the first convergence zone, vertical correlations oscillate periodically with the increase of vertical separation, and share the same distribution pattern with the sound energy along the vertical direction, which is caused by the periodical oscillation of two groups of the refracted rays from water volume. The refracted rays have the same amplitude, therefore, the time delays of the two group of rays increase with receiver depth increasing, and the phase of sound filed fluctuates in
$The research on the vertical correlation characteristics of sound field in deep water has important implications for enhancing the vertical array gain and improving the ability to detect the underwater target. Based on a deep-water experiment conducted in the South China Sea, the vertical coherence of sound fields in the direct zone, shadow zone and convergence zone are analyzed with the sound signals received by a vertical line array that covers the maximal depth to 1,866 m. The numerical analysis based on the ray theory is carried out to provide corresponding theoretical explanations to the variations of the vertical correlation characteristics at different ranges and depths. The vertical correlation coefficients in the direct zone are higher than 0.707 for the whole depth and drop very little with the increase of the vertical depth. It is because the main contributions come from direct arrival ray and sea surface reflection ray. The pulse structure is relatively simple, and the time delays of the two rays increase with the space between two receivers increasing. In the shadow zone, sound energy mainly comes from bottom reflection. Therefore, the vertical correlation coefficients are relatively low. Multi-path arrival is observed obviously. Vertical correlation coefficients drop quickly with depth increasing. With range increasing, the time delays of the multi-path pulses decrease. The vertical correlation coefficients at the same depth will increase a little with range increasing. Near the first convergence zone, vertical correlations oscillate periodically with the increase of vertical separation, and share the same distribution pattern with the sound energy along the vertical direction, which is caused by the periodical oscillation of two groups of the refracted rays from water volume. The refracted rays have the same amplitude, therefore, the time delays of the two group of rays increase with receiver depth increasing, and the phase of sound filed fluctuates in periodically. The periodicity causes the sound intensity and the vertical correlation coefficients to have the same oscillation structures. If the rays have the same phases, the main contribution comes from refraction rays, the structure of the pulses is relatively simple and causes vertical correlation to be higher. Otherwise, the main contribution comes from bottom reflected rays, the structure of the pulses is complex, and vertical correlation drops down. Corresponding Author: Li Zheng-lin $\end{document}$\left[ {0,2} {\text{π}}\right]$ periodically. The periodicity causes the sound intensity and the vertical correlation coefficients to have the same oscillation structures. If the rays have the same phases, the main contribution comes from refraction rays, the structure of the pulses is relatively simple and causes vertical correlation to be higher. Otherwise, the main contribution comes from bottom reflected rays, the structure of the pulses is complex, and vertical correlation drops down. [1] 周士弘, 张仁和, 陶晓东, 龚敏, 郝隆盛 1998 自然科学进展 8 342
 Google Scholar
Google Scholar
Zhou S H, Zhang R H, Tao X D, Gong M, Hao L S 1998 Progress in Natural Science 8 342
 Google Scholar
Google Scholar
[2] Guo L H, Gong Z X, Wu L X 2001 Chin. Phys. Lett. 18 1366
 Google Scholar
Google Scholar
[3] Li Z L, Zhang R H, Yan J, Li F H, Liu J J 2004 IEEE J. Oceanic Eng. 29 973
 Google Scholar
Google Scholar
[4] Wan L, Zhou J X, Rogers P H, Knobles D P 2009 Acoust. Phys. 55 383
 Google Scholar
Google Scholar
[5] 赵梅, 胡长青 2010 声学技术 29 365
 Google Scholar
Google Scholar
Zhao M, Hu C Q 2010 Technical Acoustics 29 365
 Google Scholar
Google Scholar
[6] 王鲁军, 彭朝晖, 李整林 2011 声学学报 36 596
Wang L J, Peng C H, Li Z L 2011 Acta Acustica 36 596
[7] 张仁和, 张双荣, 肖金泉, 孙庚辰, 王孟新 1981 声学学报 1 9
Zhang R H, Zhang S R, Xiao J Q, Sun G C, Wang M X 1981 Acta Acustica 1 9
[8] Wang Q, Zhang R H 1992 J. Acoust. Soc. Am. 92 932
 Google Scholar
Google Scholar
[9] 宫在晓 2001 博士学位论文(北京: 中国科学院声学研究所)
Gong Z X 2001 Ph. D. Dissertation (Beijing: The Institute of Acoustics of the Chinese Academy of Sciences) (in Chinese)
[10] Urick R J, Lund G R 1968 J. Acoust. Soc. Am. 43 723
 Google Scholar
Google Scholar
[11] Urick R J 1973 J. Acoust. Soc. Am. 54 115
 Google Scholar
Google Scholar
[12] Colosi J A, Chandrayadula T K, Voronovich A G, Ostashev V E 2013 J. Acoust. Soc. Am. 134 3119
 Google Scholar
Google Scholar
[13] Li J, Li Z L, Ren Y 2016 Chin. Phys. B 25 124310
 Google Scholar
Google Scholar
[14] 李鋆 2017 博士学位论文(北京: 中国科学院声学研究所)
Li J 2017 Ph. D. Dissertation (Beijing: The Institute of Acoustics of the Chinese Academy of Sciences) (in Chinese)
[15] 胡治国, 李整林, 张仁和, 任云, 秦继兴, 何利 2016 65 014303
 Google Scholar
Google Scholar
Hu Z G, Li Z L, Zhang R H, Ren Y, Qin J X, He L 2016 Acta Phys. Sin. 65 014303
 Google Scholar
Google Scholar
[16] 胡治国, 李整林, 秦继兴, 任云, 张仁和 2016 中国科学: 物理学 力学 天文学 46 094304
Hu Z G, Li Z L, Qin J X, Ren Y, Zhang R H 2016 Scientia Sinica Physica, Mechanica & Astronomica 46 094304
[17] 胡治国, 李整林, 张仁和, 任云, 李鋆 2016 声学学报 41 758
Hu Z G, Li Z L, Zhang R H, Ren Y, Li J 2016 Acta Acustica 41 758
[18] Collins M D, Westwood E K 1991 J. Acoust. Soc. Am. 89 1068
 Google Scholar
Google Scholar
[19] Collins M D 1993 J. Acoust. Soc. Am. 93 1736
 Google Scholar
Google Scholar
[20] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (2nd Ed.) (New York: Springer) p147 p36
[21] Wu S L, Li Z L, Qin J X 2015 Chin. Phys. Lett. 32 124301
 Google Scholar
Google Scholar
[22] Li Z L, Li F H 2010 Chin. J. Oceanol. Limnol. 28 990
 Google Scholar
Google Scholar
[23] Porter M B, Bucker H P 1987 J. Acoust. Soc. Am. 82 1349
 Google Scholar
Google Scholar
[24] 翁晋宝 2015 博士学位论文(北京: 中国科学院声学研究所)
Weng J B 2015 Ph. D. Dissertation (Beijing: The Institute of Acoustics of the Chinese Academy of Sciences) (in Chinese)
[25] 张仁和, 李风华 1999 中国科学 A 29 241
Zhang R H, Li F H 1999 Science in China (Series A)
29 241 [26] 翁晋宝, 李风华, 郭永刚 2015 声学学报 40 207
Weng J B, Li F H, Guo Y G 2015 Acta Acustica 40 207
[27] 翁晋宝, 李风华, 郭永刚 2016 声学学报 41 330
Weng J B, Li F H, Guo Y G 2016 Acta Acustica 41 330
-
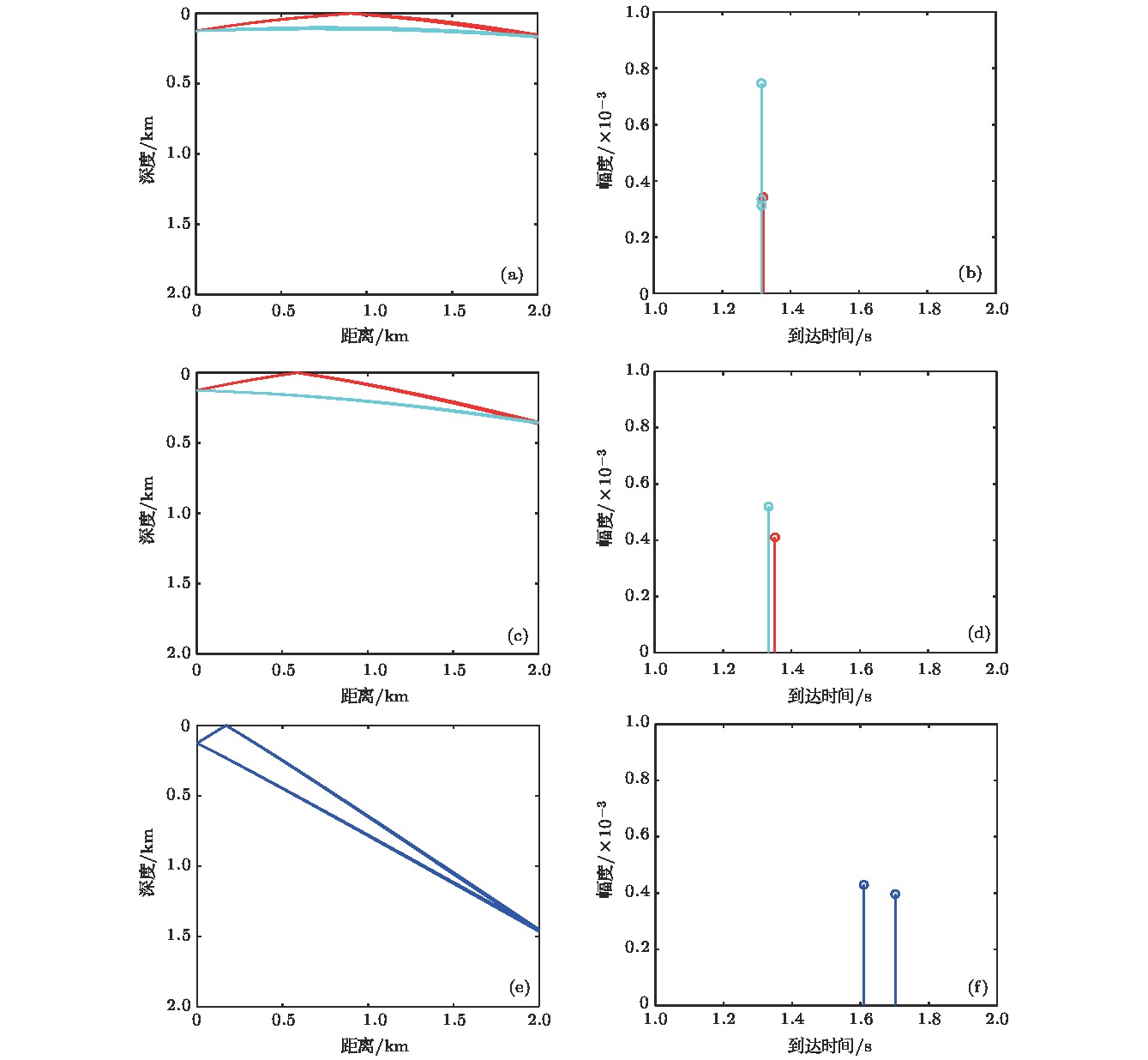
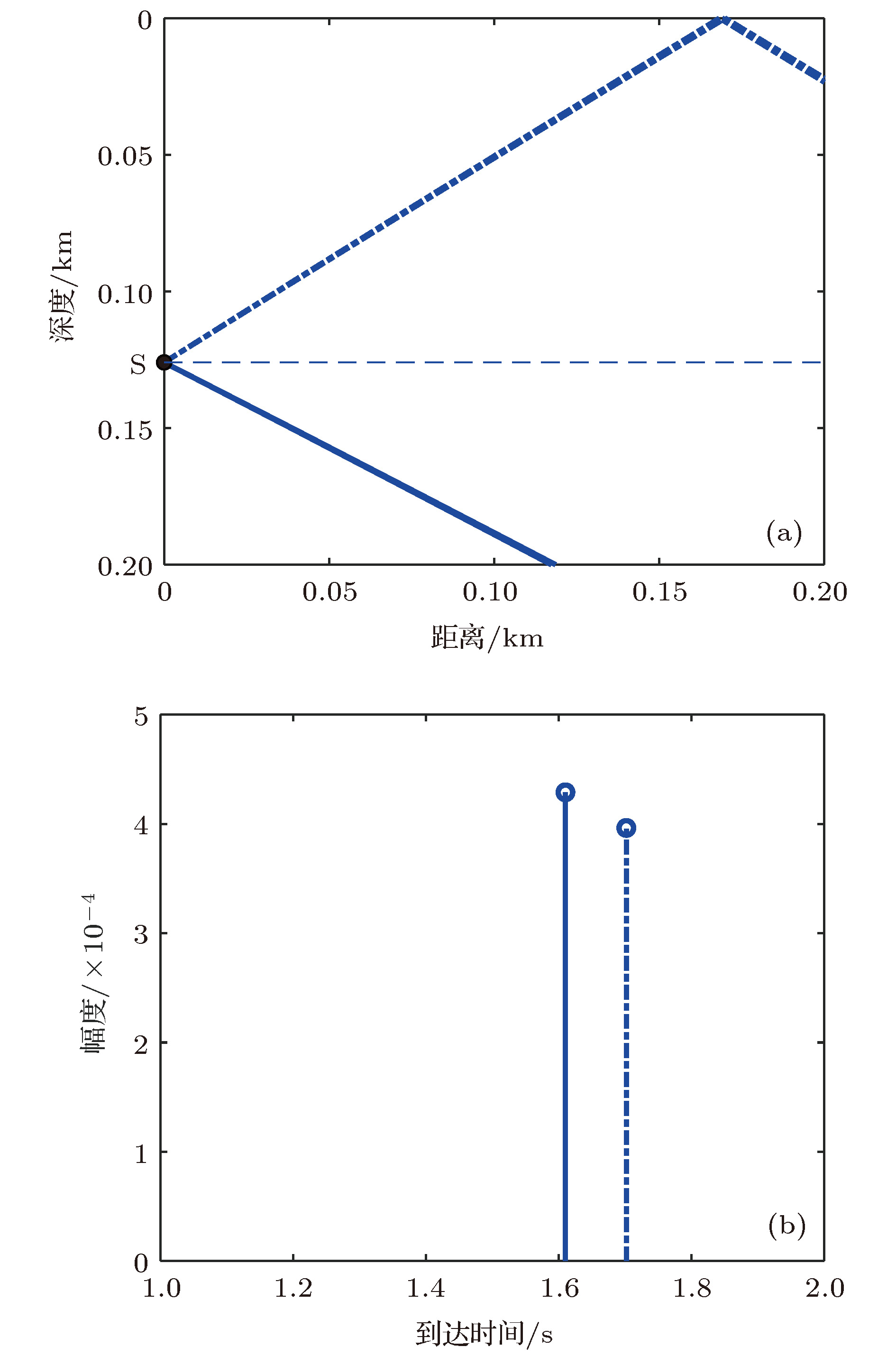
图 11 直达区内对声场起主要贡献的两条声线的初始掠射角及时间到达结构 (a) 声源处的掠射角; (b) 时间到达结构(声源深度126 m, 接收深度1453 m)
Figure 11. The two main rays contributing to the sound field in the direct zone: (a) The grazing angles at source location; (b) the arrivals of the two rays (The source and receiver are at the depth of 126 and 1453 m, respectively).
表 1 海底底质采样测量样品分析参数表
Table 1. Sediment parameters analyzed from core sampling.
深度范围/cm 实测声速/m·s–1 湿密度/g·cm–3 声衰减系数/dB·m–1 孔隙度/% 中值粒径/mm 沉积物类型 0–28 1583 1.65 137.06 62.60 0.0053 粘土质粉砂 28–55 1597 1.56 74.02 65.08 0.0274 粉砂 55–80 1663 1.57 118.80 67.59 0.0287 粉砂 80–105 1695 1.45 127.50 74.93 0.0127 粘土质粉砂 105–130 1631 1.55 108.91 68.22 0.0157 粉砂 130–155 1516 1.44 104.86 75.38 0.0062 粘土质粉砂 155–180 129 1.37 66.73 77.98 0.0059 粘土质粉砂 180–205 1508 1.33 127.47 80.77 0.0052 粘土质粉砂 205–230 1540 1.30 111.89 84.07 0.0046 粘土质粉砂 230–250 1533 1.26 121.37 85.00 0.0050 粘土质粉砂 250–280 1547 1.26 159.41 85.55 0.0057 粘土质粉砂 280–305 1565 1.21 255.70 83.24 0.0045 粘土质粉砂 平均值 1584 1.41 126.14 75.87 0.0106 –- -
[1] 周士弘, 张仁和, 陶晓东, 龚敏, 郝隆盛 1998 自然科学进展 8 342
 Google Scholar
Google Scholar
Zhou S H, Zhang R H, Tao X D, Gong M, Hao L S 1998 Progress in Natural Science 8 342
 Google Scholar
Google Scholar
[2] Guo L H, Gong Z X, Wu L X 2001 Chin. Phys. Lett. 18 1366
 Google Scholar
Google Scholar
[3] Li Z L, Zhang R H, Yan J, Li F H, Liu J J 2004 IEEE J. Oceanic Eng. 29 973
 Google Scholar
Google Scholar
[4] Wan L, Zhou J X, Rogers P H, Knobles D P 2009 Acoust. Phys. 55 383
 Google Scholar
Google Scholar
[5] 赵梅, 胡长青 2010 声学技术 29 365
 Google Scholar
Google Scholar
Zhao M, Hu C Q 2010 Technical Acoustics 29 365
 Google Scholar
Google Scholar
[6] 王鲁军, 彭朝晖, 李整林 2011 声学学报 36 596
Wang L J, Peng C H, Li Z L 2011 Acta Acustica 36 596
[7] 张仁和, 张双荣, 肖金泉, 孙庚辰, 王孟新 1981 声学学报 1 9
Zhang R H, Zhang S R, Xiao J Q, Sun G C, Wang M X 1981 Acta Acustica 1 9
[8] Wang Q, Zhang R H 1992 J. Acoust. Soc. Am. 92 932
 Google Scholar
Google Scholar
[9] 宫在晓 2001 博士学位论文(北京: 中国科学院声学研究所)
Gong Z X 2001 Ph. D. Dissertation (Beijing: The Institute of Acoustics of the Chinese Academy of Sciences) (in Chinese)
[10] Urick R J, Lund G R 1968 J. Acoust. Soc. Am. 43 723
 Google Scholar
Google Scholar
[11] Urick R J 1973 J. Acoust. Soc. Am. 54 115
 Google Scholar
Google Scholar
[12] Colosi J A, Chandrayadula T K, Voronovich A G, Ostashev V E 2013 J. Acoust. Soc. Am. 134 3119
 Google Scholar
Google Scholar
[13] Li J, Li Z L, Ren Y 2016 Chin. Phys. B 25 124310
 Google Scholar
Google Scholar
[14] 李鋆 2017 博士学位论文(北京: 中国科学院声学研究所)
Li J 2017 Ph. D. Dissertation (Beijing: The Institute of Acoustics of the Chinese Academy of Sciences) (in Chinese)
[15] 胡治国, 李整林, 张仁和, 任云, 秦继兴, 何利 2016 65 014303
 Google Scholar
Google Scholar
Hu Z G, Li Z L, Zhang R H, Ren Y, Qin J X, He L 2016 Acta Phys. Sin. 65 014303
 Google Scholar
Google Scholar
[16] 胡治国, 李整林, 秦继兴, 任云, 张仁和 2016 中国科学: 物理学 力学 天文学 46 094304
Hu Z G, Li Z L, Qin J X, Ren Y, Zhang R H 2016 Scientia Sinica Physica, Mechanica & Astronomica 46 094304
[17] 胡治国, 李整林, 张仁和, 任云, 李鋆 2016 声学学报 41 758
Hu Z G, Li Z L, Zhang R H, Ren Y, Li J 2016 Acta Acustica 41 758
[18] Collins M D, Westwood E K 1991 J. Acoust. Soc. Am. 89 1068
 Google Scholar
Google Scholar
[19] Collins M D 1993 J. Acoust. Soc. Am. 93 1736
 Google Scholar
Google Scholar
[20] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (2nd Ed.) (New York: Springer) p147 p36
[21] Wu S L, Li Z L, Qin J X 2015 Chin. Phys. Lett. 32 124301
 Google Scholar
Google Scholar
[22] Li Z L, Li F H 2010 Chin. J. Oceanol. Limnol. 28 990
 Google Scholar
Google Scholar
[23] Porter M B, Bucker H P 1987 J. Acoust. Soc. Am. 82 1349
 Google Scholar
Google Scholar
[24] 翁晋宝 2015 博士学位论文(北京: 中国科学院声学研究所)
Weng J B 2015 Ph. D. Dissertation (Beijing: The Institute of Acoustics of the Chinese Academy of Sciences) (in Chinese)
[25] 张仁和, 李风华 1999 中国科学 A 29 241
Zhang R H, Li F H 1999 Science in China (Series A)
29 241 [26] 翁晋宝, 李风华, 郭永刚 2015 声学学报 40 207
Weng J B, Li F H, Guo Y G 2015 Acta Acustica 40 207
[27] 翁晋宝, 李风华, 郭永刚 2016 声学学报 41 330
Weng J B, Li F H, Guo Y G 2016 Acta Acustica 41 330
Catalog
Metrics
- Abstract views: 22953
- PDF Downloads: 212
- Cited By: 0















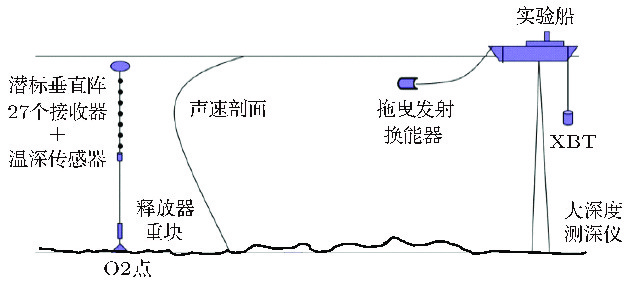
 DownLoad:
DownLoad: