-
Wide-band gap SiC is a promising semiconductor material for microelectronic applications due to its superior electronic properties, high thermal conductivity, chemical and radiation stability, and extremely high break-down voltage. Over the past several years, tremendous advances have been made in SiC crystal growth technology. Nevertheless, SiC will not reach its anticipated potential until a variety of problems are solved, one of the problem is step bunching during step flow growth of SiC, because it could lead to uneven distribution of impurity and less smooth surfaces. In this paper, step bunching morphologies on vicinal 4H-SiC (0001) surfaces with the miscut toward
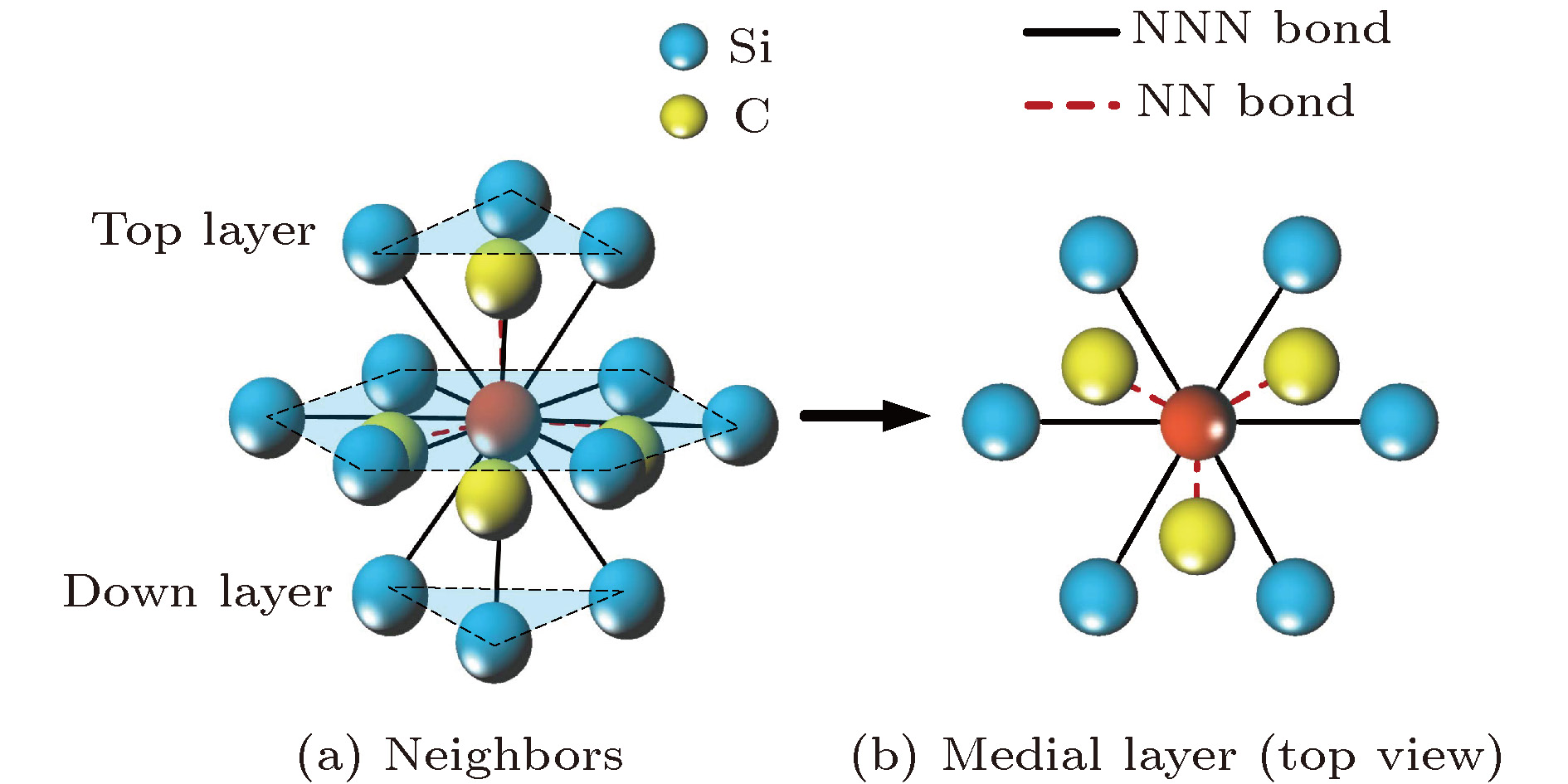
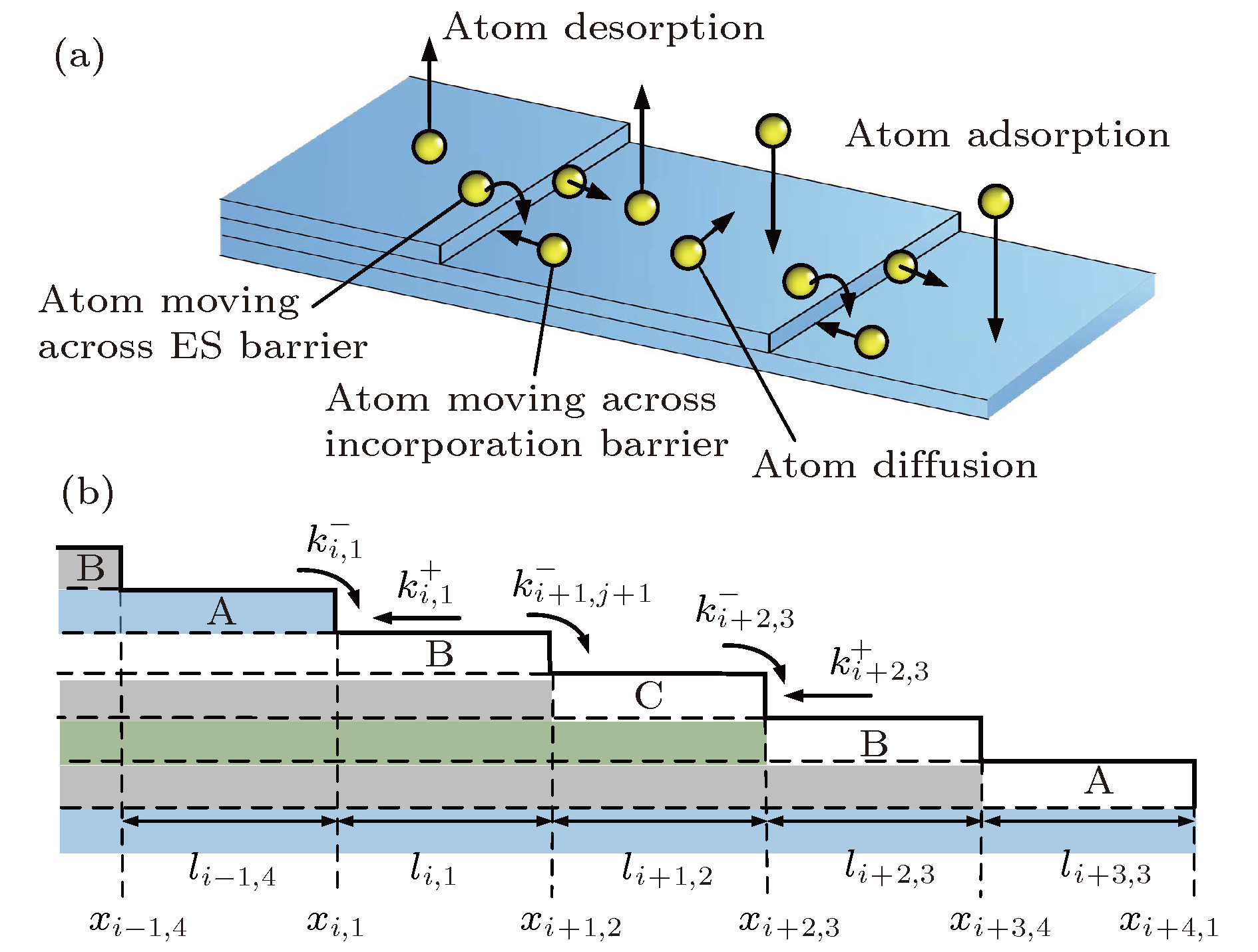
$\left[ {1\bar 100} \right]$ or$\left[ {11\bar 20} \right]$ directions are studied with a three-dimensional kinetic Monte Carlo model, and then compared with the analytic model based on the theory of Burton-Cabera-Frank. In the kinetic Monte Carlo model, based on the crystal lattice of 4H-SiC, a lattice mesh is established to fix the positions of atoms and bond partners. The events considered in the model are adsorption and diffusion of adatoms on the terraces, attachment, detachment and interlayer transport of adatoms at the step edges. The effects of Ehrlich-Schwoebel barriers at downward step edges and inverse Schwoebel barrier at upwards step edges are also considered. In addition, to obtain more elaborate information about the behavior of atoms in the crystal surface, silicon and carbon atoms are treated as the minimal diffusing species. Finally, the periodic boundary conditions are applied to the lateral direction while the " helicoidal boundary conditions” are used in the direction of crystal growth. The simulation results show that four bilayer-height steps are formed on the vicinal 4H-SiC (0001) surfaces with the miscut toward$\left[ {1\bar 100} \right]$ direction, while along the$\left[ {11\bar 20} \right]$ direction, only bunches with two-bilayer-height are formed. Moreover, zigzag shaped edges are observed for 4H-SiC (0001) vicinal surfaces with the miscut toward$\left[ {11\bar 20} \right]$ direction. The formation of these step bunching morphologies on vicinal surfaces with different miscut directions are related to the extra energy and step barrier. The different extra energy for each bilayer plane results in step bunches with two-bilayer-height on the vicinal 4H-SiC (0001) surface. And the step barriers finally lead to the formation of step bunches with four-bilayer-height. Finally, the formation mechanism of the stepped morphology is also analyzed by a one-dimensional Burton-Cabera-Frank analytic model. In the model, the parameters are corresponding to those used in the kinetic Monte Carlo model, and then solved numerically. The evolution characteristic of step bunching calculated by the Burton-Cabera-Frank model is consistent with the results obtained by the kinetic Monte Carlo simulation.-
Keywords:
- silicon carbide /
- step bunching /
- Monte Carlo /
- crystal growth
[1] Kimoto T 2016 Prog. Cryst. Growth Charact. Mater. 62 329
Google Scholar
[2] Tsunenobu K 2015 Jpn. J. Appl. Phys. 54 040103
Google Scholar
[3] 唐超, 吉璐, 孟利军, 孙立忠, 张凯旺, 钟建新 2009 58 7815
Google Scholar
Tang C, Ji L, Meng L J, Sun L Z, Zhang K W, Zhong J X, 2009 Acta Phys. Sin. 58 7815
Google Scholar
[4] 冯倩, 郝跃, 张晓菊, 刘玉龙 2004 53 626
Google Scholar
Feng Q, Hao Y, Zhang X J, Liu Y L 2004 Acta Phys. Sin. 53 626
Google Scholar
[5] 杨慧慧, 高峰, 戴明金, 胡平安 2017 66 216804
Google Scholar
Yang H H, Gao F, Dai M J, Hu P A 2017 Acta Phys. Sin. 66 216804
Google Scholar
[6] La V F, Severino A, Anzalone R, Bongiorno C, Litrico G, Mauceri M, Schoeler M, Schuh P, Wellmann P 2018 Mater. Sci. Semicond. Process. 78 57
Google Scholar
[7] Müller S G, Sanchez E K, Hansen D M, Drachev R D, Chung G, Thomas B, Zhang J, Loboda M J, Dudley M, Wang H, Wu F, Byrappa S, Raghothamachar B, Choi G 2012 J. Cryst. Growth 352 39
Google Scholar
[8] Tomoki Y, Ohtomo K, Sato S, Ohtani N, Katsuno M, Fujimoto T, Sato S, Tsuge H, Yano T 2015 J. Cryst. Growth 431 24
Google Scholar
[9] Schwoebel R L 1969 J. Appl. Phys. 40 614
Google Scholar
[10] Kimoto T, Itoh A, Matsunami H, Okano T 1997 J. Appl. Phys. 81 3494
Google Scholar
[11] Kimoto T, Itoh A, Matsunami H 1995 Appl. Phys. Lett. 66 3645
Google Scholar
[12] Ohtani N, Katsuno M, Aigo T, Fujimoto T, Tsuge H, Yashiro H, Kanaya M 2000 J. Cryst. Growth 210 613
Google Scholar
[13] Heuell P, Kulakov M A, Bullemer B 1995 Surf. Sci. 331-333 965
[14] Borovikov V, Zangwill A 2009 Phys. Rev. B 79 245413
Google Scholar
[15] Krzyżewski F 2014 J. Cryst. Growth 401 511
Google Scholar
[16] Xie M H, Leung S Y, Tong S Y 2002 Surf. Sci. 515 L459
Google Scholar
[17] Krzyżewski F, Załuska–Kotur M A 2014 J. Appl. Phys. 115 213517
Google Scholar
[18] Li Y, Chen X J, Su J 2016 Appl. Surf. Sci. 371 242
Google Scholar
[19] Battaile C C 2008 Comput. Methods Appl. Mech. Engrg. 197 3386
Google Scholar
[20] Chien F R, Nutt S R, Yoo W S, Kimoto T, Matsunami H 1994 J. Mater. Res. 9 940
Google Scholar
[21] Heine V, Cheng C, Needs R J 1991 J. Am. Ceram. Soc. 74 2630
Google Scholar
[22] Li Y, Chen X, Su J 2017 J. Cryst. Growth 468 28
Google Scholar
[23] Camarda M, La Magna A, La Via F 2007 J. Comput. Phys. 227 1075
Google Scholar
[24] Ohtani N, Katsuno M, Takahashi J, Yashiro H, Kanaya M 1999 Phys. Rev. B 59 4592
Google Scholar
[25] Sato M 2018 Phys. Rev. E 97 062801
Google Scholar
[26] Ranguelov B, Müller P, Metois J J, Stoyanov S 2017 J. Cryst. Growth 457 184
Google Scholar
[27] Markov I V 2003 Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy (London: World Scientific)
[28] Vasiliauskas R, Marinova M, Hens P, Wellmann P, Syväjärvi, Yakimova R 2012 Cryst. Growth Des. 12 197
[29] Mochizuki K 2008 Appl. Phys. Lett. 93 222108
Google Scholar
-
图 1 4H-SiC晶体结构示意图
Figure 1. Schematic crystal structure of 4H-SiC.
图 2 (a)邻位关系计算模型; (b)中间层俯视图
Figure 2. (a) The calculation model of neighbors; (b) top view of medial layer.
图 3 4H-SiC (0001)面偏向
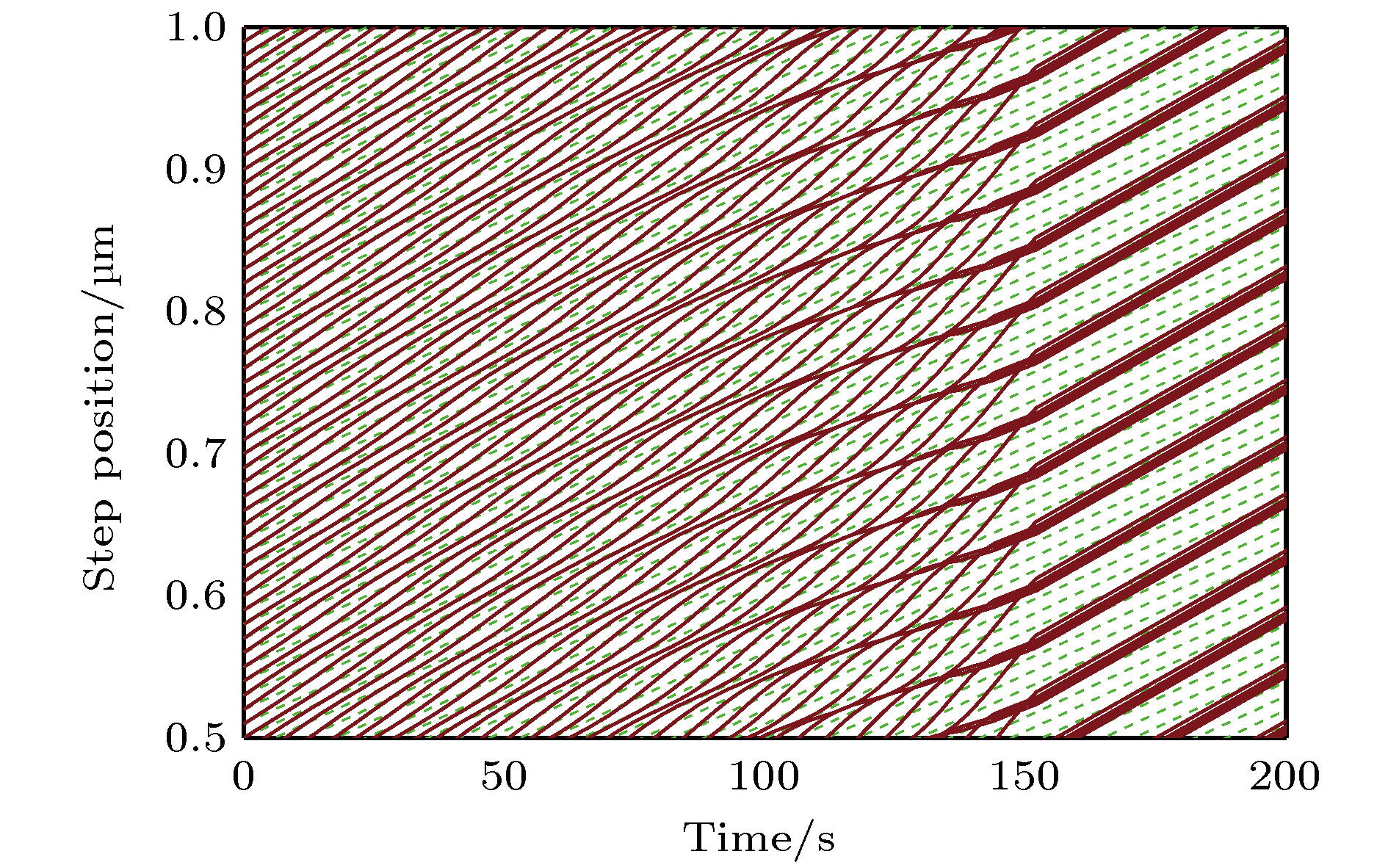
$\left[ {1\bar 100} \right]$ 的台阶形貌演化 (a)初始台阶; (b) AB (蓝)与 BC (浅蓝)聚并台阶的形成; (c) 四层台阶聚并Figure 3. The evolution of stepped morphology on 4H-SiC (0001) surface with miscut toward
$\left[ {1\bar 100} \right]$ direction: (a) Initial stage; (b) formation of two-bilayer-height AB (blue) steps and CB (light blue); (c) bunching of four bilayers.
图 4 4H-SiC (0001)面偏向
$\left[ {11\bar 20} \right]$ 的台阶形貌演化 (a)初始台阶; (b) AB (蓝)与 BC (浅蓝)聚并台阶的形成; (c) 两层台阶形成的聚并扭折台阶Figure 4. The evolution of stepped morphology on 4H-SiC (0001) surface with miscut toward
$\left[ {11\bar 20} \right]$ direction: (a) Initial stage; (b) formation of two-bilayer-height CB (light blue) and AB (blue) steps; (c) formation of two-bilayer-height steps with zigzag shapes.
图 5 不同类型台阶键的配置方式 (a)SN型台阶; (b)SD型台阶; (c)SM型台阶
Figure 5. The difference in bond configurations are shown schematically: (a) Type of SN step edge; (b) type of SD step edge; (c) type of SM step edge.
图 6 台阶流动生长中SiC晶体邻晶面示意图 (a)台阶表面事件与能量势垒; (b)台阶侧面
Figure 6. Schematic top and side view of a vicinal surface during step-flow growth: (a) The events occurring on the surface and energy barriers; (b) side view of a vicinal surface.
图 7 4H-SiC (0001)面偏向
$\left[ {1\bar 100} \right]$ 方向台阶轨迹Figure 7. Step trajectories of the vicinal surface with miscut angles towards
$\left[ {1\bar 100} \right]$ direction.
图 8 4H-SiC (0001)面偏向
$\left[ {11\bar 20} \right]$ 方向台阶轨迹Figure 8. Step trajectories of the vicinal surface with miscut angles towards
$\left[ {11\bar 20} \right]$ direction. -
[1] Kimoto T 2016 Prog. Cryst. Growth Charact. Mater. 62 329
Google Scholar
[2] Tsunenobu K 2015 Jpn. J. Appl. Phys. 54 040103
Google Scholar
[3] 唐超, 吉璐, 孟利军, 孙立忠, 张凯旺, 钟建新 2009 58 7815
Google Scholar
Tang C, Ji L, Meng L J, Sun L Z, Zhang K W, Zhong J X, 2009 Acta Phys. Sin. 58 7815
Google Scholar
[4] 冯倩, 郝跃, 张晓菊, 刘玉龙 2004 53 626
Google Scholar
Feng Q, Hao Y, Zhang X J, Liu Y L 2004 Acta Phys. Sin. 53 626
Google Scholar
[5] 杨慧慧, 高峰, 戴明金, 胡平安 2017 66 216804
Google Scholar
Yang H H, Gao F, Dai M J, Hu P A 2017 Acta Phys. Sin. 66 216804
Google Scholar
[6] La V F, Severino A, Anzalone R, Bongiorno C, Litrico G, Mauceri M, Schoeler M, Schuh P, Wellmann P 2018 Mater. Sci. Semicond. Process. 78 57
Google Scholar
[7] Müller S G, Sanchez E K, Hansen D M, Drachev R D, Chung G, Thomas B, Zhang J, Loboda M J, Dudley M, Wang H, Wu F, Byrappa S, Raghothamachar B, Choi G 2012 J. Cryst. Growth 352 39
Google Scholar
[8] Tomoki Y, Ohtomo K, Sato S, Ohtani N, Katsuno M, Fujimoto T, Sato S, Tsuge H, Yano T 2015 J. Cryst. Growth 431 24
Google Scholar
[9] Schwoebel R L 1969 J. Appl. Phys. 40 614
Google Scholar
[10] Kimoto T, Itoh A, Matsunami H, Okano T 1997 J. Appl. Phys. 81 3494
Google Scholar
[11] Kimoto T, Itoh A, Matsunami H 1995 Appl. Phys. Lett. 66 3645
Google Scholar
[12] Ohtani N, Katsuno M, Aigo T, Fujimoto T, Tsuge H, Yashiro H, Kanaya M 2000 J. Cryst. Growth 210 613
Google Scholar
[13] Heuell P, Kulakov M A, Bullemer B 1995 Surf. Sci. 331-333 965
[14] Borovikov V, Zangwill A 2009 Phys. Rev. B 79 245413
Google Scholar
[15] Krzyżewski F 2014 J. Cryst. Growth 401 511
Google Scholar
[16] Xie M H, Leung S Y, Tong S Y 2002 Surf. Sci. 515 L459
Google Scholar
[17] Krzyżewski F, Załuska–Kotur M A 2014 J. Appl. Phys. 115 213517
Google Scholar
[18] Li Y, Chen X J, Su J 2016 Appl. Surf. Sci. 371 242
Google Scholar
[19] Battaile C C 2008 Comput. Methods Appl. Mech. Engrg. 197 3386
Google Scholar
[20] Chien F R, Nutt S R, Yoo W S, Kimoto T, Matsunami H 1994 J. Mater. Res. 9 940
Google Scholar
[21] Heine V, Cheng C, Needs R J 1991 J. Am. Ceram. Soc. 74 2630
Google Scholar
[22] Li Y, Chen X, Su J 2017 J. Cryst. Growth 468 28
Google Scholar
[23] Camarda M, La Magna A, La Via F 2007 J. Comput. Phys. 227 1075
Google Scholar
[24] Ohtani N, Katsuno M, Takahashi J, Yashiro H, Kanaya M 1999 Phys. Rev. B 59 4592
Google Scholar
[25] Sato M 2018 Phys. Rev. E 97 062801
Google Scholar
[26] Ranguelov B, Müller P, Metois J J, Stoyanov S 2017 J. Cryst. Growth 457 184
Google Scholar
[27] Markov I V 2003 Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy (London: World Scientific)
[28] Vasiliauskas R, Marinova M, Hens P, Wellmann P, Syväjärvi, Yakimova R 2012 Cryst. Growth Des. 12 197
[29] Mochizuki K 2008 Appl. Phys. Lett. 93 222108
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 15589
- PDF Downloads: 391
- Cited By: 0
