-
Experimental and theoretical studies have shown that a single magnon mode and cavity photon can be coupled coherently and dissipatively, with the interference between two types of coupling creating zero damping effect. In magnetic bilayers or multilayers, there exists more than one magnon mode which can be directly coupled by interface exchange interaction. In this work, a single-magnon mode is extended to a two-magnon mode and the effect of the two-magnon mode on zero damping condition is investigated. Using eigenfrequency analysis and microwave transmission spectra, the analytical expressions of the zero damping condition and the frequency detuning can be derived. By comparing analytical results with numerical results, the dependence of zero damping condition on system parameters can be obtained. In the absence of direct interface exchange magnon-magnon coupling, the zero damping condition occurs for dissipative coupling or hybrid coupling. As the coupling strength increases, the distance between two zero damping points increases. For hybrid coupling, the two zero damping points turn no longer symmetric, which is different from the case of pure coupling. Moreover, the effect of interface exchange magnon-magnon interaction on zero damping condition is studied. The interface exchange coupling results in the splitting of microwave transmission spectra, but the zero damping condition occurs only in the low-frequency mode. As the interface exchange coupling strength increases, the frequency at which the zero damping condition happens will shift toward lower frequency. Due to extremely narrow line-width of microwave transmission dip under the zero damping condition, the result in this work is expected to be useful for designing the magnon-based quantum sensing devices.
-
Keywords:
- magnon /
- microwave cavity /
- zero damping condition
[1] Zhang X F, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401
 Google Scholar
Google Scholar
[2] Soykal O O, Flatt´e M E 2010 Phys. Rev. Lett. 104 077202
 Google Scholar
Google Scholar
[3] Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2015 Science 349 405
 Google Scholar
Google Scholar
[4] Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003
 Google Scholar
Google Scholar
[5] Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603
 Google Scholar
Google Scholar
[6] Goryachev M, Farr W G, Creedon D L, Fan Y, Kostylev M, Tobar M E 2014 Phys. Rev. Appl. 2 054002
 Google Scholar
Google Scholar
[7] Cao Y, Yan P, Huebl H, Goennenwein S T B, Bauer G E W 2015 Phys. Rev. B 91 094423
 Google Scholar
Google Scholar
[8] Bai L, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201
 Google Scholar
Google Scholar
[9] Bernier N R, T´oth L D, Feofanov A K, Kippenberg T J 2018 Phys. Rev. A 98 023841
 Google Scholar
Google Scholar
[10] Yu W C, Wang J J, Yuan H Y, Xiao J 2019 Phys. Rev. Lett. 123 227201
 Google Scholar
Google Scholar
[11] Grigoryan V L, Shen K, Xia K 2018 Phys. Rev. B 98 024406
 Google Scholar
Google Scholar
[12] Wu W J, Xu D, Qian J, Li J, Wang Y P, You J Q 2022 Chin. Phys. B 31 127503
 Google Scholar
Google Scholar
[13] Bao X X, Guo G F, Yang X, Tan L 2023 Chin. Phys. B 32 080301
 Google Scholar
Google Scholar
[14] Liao Q, Peng K, Qiu H 2023 Chin. Phys. B 32 054205
 Google Scholar
Google Scholar
[15] Liu T, Zhang X, Tang H X, Flatte M E 2016 Phys. Rev. B 94 060405(R
 Google Scholar
Google Scholar
[16] Zare R B, Viola K S, Haigh J A, Usami K, Lachance-Quirion D, Nakamura Y, Hu C M, Tang H X, Bauer G E, Blanter Y M 2022 Phys. Rep. 979 1
 Google Scholar
Google Scholar
[17] Harder M, Yao B, Gui Y, Hu C M 2021 J. Appl. Phys. 129 201101
 Google Scholar
Google Scholar
[18] Yuan H, Cao Y, Kamra A, Duine R A, Yan P 2022 Phys. Rep. 965 1
 Google Scholar
Google Scholar
[19] Lachance-Quirion D, Tabuchi Y, Gloppe A, Usami K, Nakamura Y 2019 Appl. Phys. Exp. 12 070101
 Google Scholar
Google Scholar
[20] Lachance-Quirion D, Wolski S P, Tabuchi Y, Kono S, Usami K, Nakamura Y 2020 Science 367 425
 Google Scholar
Google Scholar
[21] Pan H, Yang Y, An Z H, Hu C M 2022 Phys. Rev. B 106 054425
 Google Scholar
Google Scholar
[22] Hyde P, Yao B M, Gui Y S, Zhang G Q, You J Q, Hu C M 2018 Phys. Rev. B 98 174423
 Google Scholar
Google Scholar
[23] Bi M X, Yan X H, Xiao Y, Dai C J 2019 J. Appl. Phys. 126 173902
 Google Scholar
Google Scholar
[24] Bi M X, Yan X H, Zhang Y, Xiao Y 2021 Phys. Rev. B 103 104411
 Google Scholar
Google Scholar
[25] Wang Y P, Zhang G Q, Zhang D, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202
 Google Scholar
Google Scholar
[26] Sharma S, Bittencourt V A S V, Karenowska A D, Kusminskiy S V 2021 Phys. Rev. B 103 L100403
 Google Scholar
Google Scholar
[27] Hei X L, Li P B, Pan X F, Nor F 2023 Phys. Rev. Lett. 130 073602
 Google Scholar
Google Scholar
[28] Yuan H Y, Yan P, Zheng S, He Q Y, Xia K, Yung M H 2020 Phys. Rev. Lett. 124 053602
 Google Scholar
Google Scholar
[29] Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601
 Google Scholar
Google Scholar
[30] Yang J Y, Zhao C S, Wang D W, Peng R, Zhou L 2024 Phys. Rev. Appl. 21 044056
 Google Scholar
Google Scholar
[31] Sun F X, Zheng S S, Xiao Y, Gong Q, He Q, Xia K 2021 Phys. Rev. Lett. 127 087203
 Google Scholar
Google Scholar
[32] Osada A, Hisatomi R, Noguchi A, Tabuchi Y, Yamazaki R, Usami K, Sadgrove M, Yalla R, Nomura M, Nakamura Y 2016 Phys. Rev. Lett. 116 223601
 Google Scholar
Google Scholar
[33] Haigh J A, Nunnenkamp A, Ramsay A J, Ferguson A J 2016 Phys. Rev. Lett. 117 133602
 Google Scholar
Google Scholar
[34] Zhang X F, Zhu N, Zou C L, Tang H X 2016 Phys. Rev. Lett. 117 123605
 Google Scholar
Google Scholar
[35] Osada A, Gloppe A, Hisatomi R, Noguchi A, Yamazaki R, Nomura M, Nakamura Y, Usami K 2018 Phys. Rev. Lett. 120 133602
 Google Scholar
Google Scholar
[36] Harder M, Yang Y, Yao B M, Yu C H, Rao J W, Gui Y S, Stamps R L, Hu C M 2018 Phys. Rev. Lett. 121 137203
 Google Scholar
Google Scholar
[37] Yang Y, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2019 Phys. Rev. Appl. 11 054023
 Google Scholar
Google Scholar
[38] Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202
 Google Scholar
Google Scholar
[39] Zhang X F, Zou C, Zhu N, Marquardt F, Jiang L, Tang H X 2015 Nat. Commun. 6 8914
 Google Scholar
Google Scholar
[40] Nair J M P, Mukhopadhyay D, Agarwal G S 2022 Phys. Rev. B 105 214418
 Google Scholar
Google Scholar
[41] Zhang Q, Xue J S, Sun Y T, Guo J J, Chen Y X, Tian Y F, Yan S S, Bai L H 2021 Phys. Rev. B 104 094303
 Google Scholar
Google Scholar
[42] Zhang D S, Song W J, Chai G Z 2017 J. Phys. D: Appl. Phys. 50 205003
 Google Scholar
Google Scholar
[43] An K, Kohno R, Litvinenko A N, Seeger R L, Naletov V V, Vila L, De Loubens G, Youssef J B, Vukadinovic N, Bauer G E W, Slavin A N, Tiberkevich V S, Klein O 2022 Phys. Rev. X 12 011060
[44] Tserkovnyak Y, Brataas A, Bauer G E W, Halperin B I 2005 Rev. Mod. Phys. 77 1375
 Google Scholar
Google Scholar
[45] Ma K, Li C, Hao Z, Ong C K, Chai G 2023 Phys. Rev. B 108 094422
 Google Scholar
Google Scholar
[46] Zhan X X, Zhang Y, Yan X H, Xiao Y 2021 J. Appl. Phys. 130 123901
 Google Scholar
Google Scholar
[47] Mahan G D 2000 Many-Particle Physics (Kluwer Academic/Plenum Publishers
[48] Holstein T, Primakoff H 1940 Phys. Rev. 58 1098
 Google Scholar
Google Scholar
[49] Chen J L, Liu C P, Liu T, Xiao Y, Xia K, Bauer G E W, Wu M Z, Yu H M 2018 Phys. Rev. Lett. 120 217202
 Google Scholar
Google Scholar
-
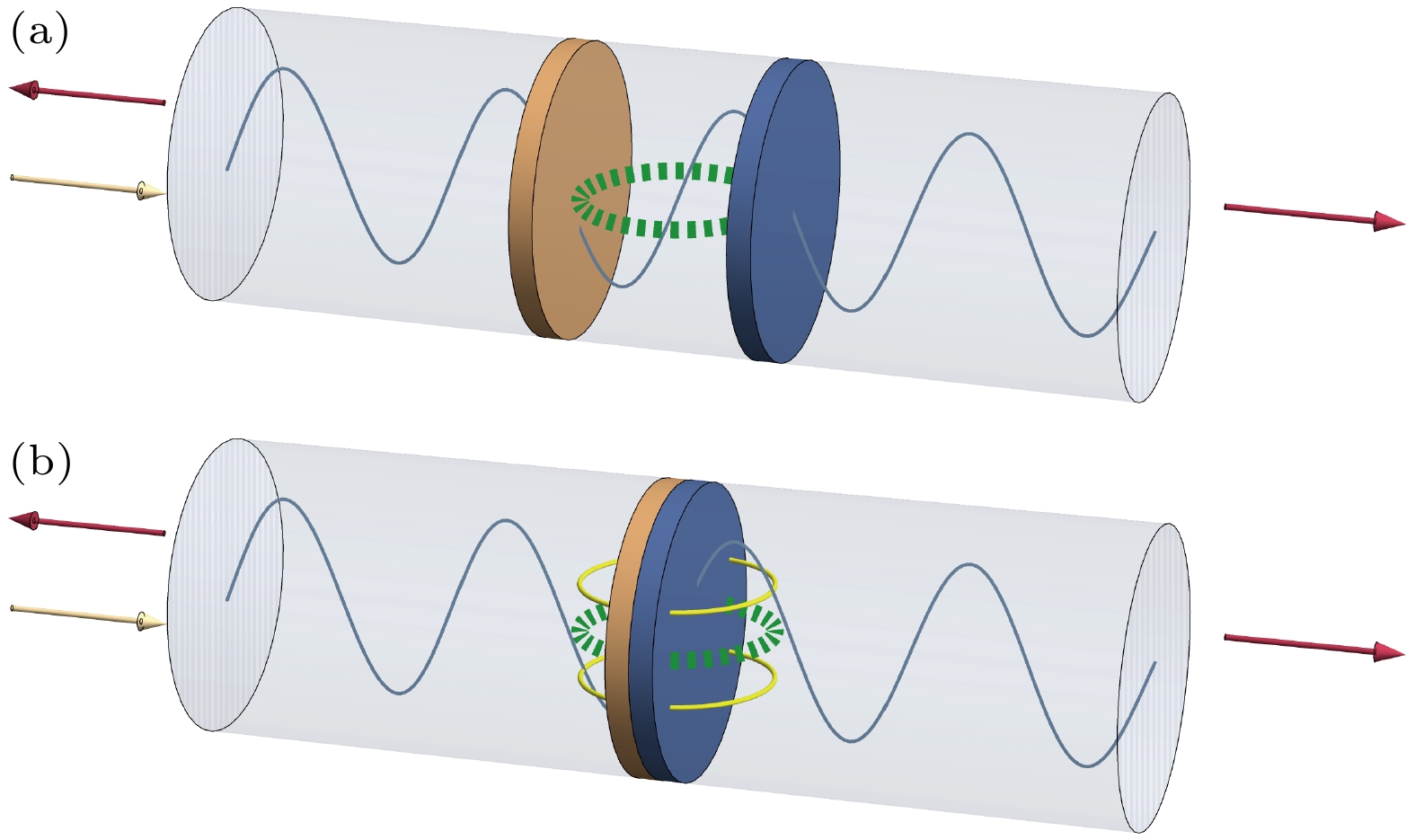
图 1 微波谐振腔(灰色长圆柱)与两个磁性层(棕色与蓝色圆盘)的器件模型 (a) 微波从外部源入射到谐振腔的左端口, 一部分反射, 另一部分进入腔内并形成驻波(黑色振荡曲线), 然后从右端口出射, 两个磁性层放在谐振腔的不同位置, 在外磁场下形成两个磁子模式, 这两个磁子模式通过相干型或耗散型耦合机制同时与谐振腔光子耦合, 从而在两个磁子模式之间形成间接的耦合作用(绿色虚线圆); (b)不同于(a), 两个磁性层放在一起, 除了谐振腔辅助的间接耦合作用(绿色虚线圆)之外, 两个磁子模式也通过界面交换耦合形成直接耦合作用(黄色实线圆)
Figure 1. Schematic of devices containing microwave cavity (long grey cylinder) and two magnetic layers (brown and blue disks): (a) The microwave is fed to the input port of cavity and experiences reflection and transmission, the transmitted wave gives rise to standing wave inside the cavity due to multiple reflections, and then exits the output port of cavity. Two magnetic layers are placed at distinct positions of cavity and excite two magnon modes under external magnetic field and microwave driving, an indirect coupling of two magnon modes occurs (green dashed circle) due to simultaneous coherent/dissipative coupling of two magnon modes with the common cavity modes; (b) contrary to (a), two magnetic layers are placed together, the interface exchange coupling in the magnetic bilayer results in direct magnon-magnon coupling (yellow solid circle) besides the aforementioned indirect coupling (green dashed circle).
图 2 单个磁子模式的微波透射谱和本征频率虚部, 纯的耗散型耦合($ G= -{\mathrm{i}}\varGamma $)的微波透射谱 (a) $ \varGamma $= 30 MHz, (b) $ \varGamma $= 60 MHz; 纯的相干型耦合($ G= g $)的微波透射谱 (c) $ g $= 30 MHz, (d) $ g $= 60 MHz; (e)—(h)分别给出了(a)—(d)对应的本征频率虚部与频率失谐$ {\varDelta }_{{\mathrm{mc}}} $的变化关系
Figure 2. Microwave transmission spectra and imaginary parts of eigenfrequency for single magnon mode, microwave transmission spectra of pure dissipative coupling ($ G= -{\mathrm{i}}\varGamma $) with (a) $ \varGamma $= 30 MHz, (b) $ \varGamma $= 60 MHz; pure coherent coupling ($ G= g $) with (c) $ g $= 30 MHz, (d) $ g $= 60 MHz; (e)–(h) imaginary parts of eigenfrequency as function of detuning $ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $ for each coupling in (a)–(d)
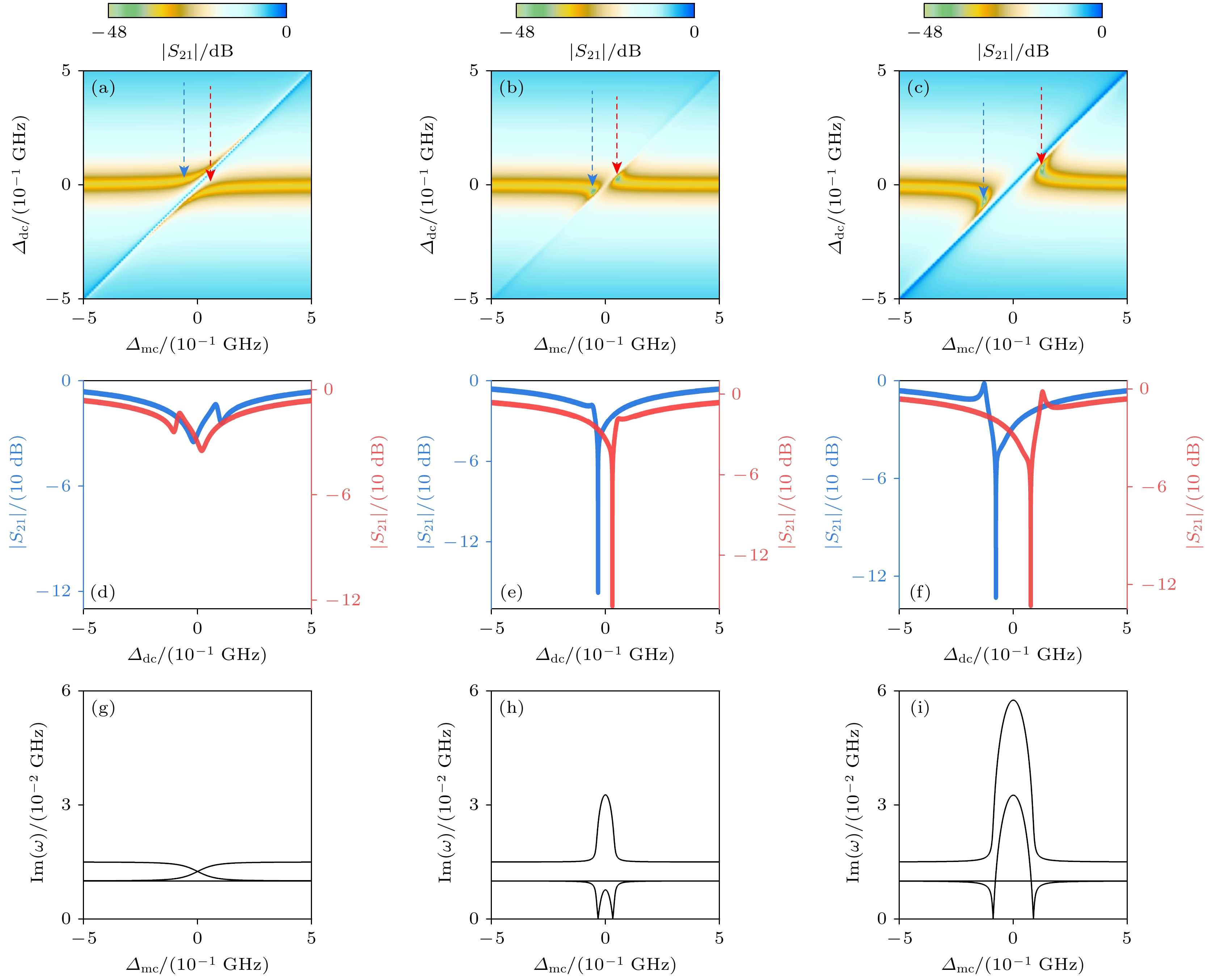
图 3 两个磁子模式的微波透射谱和本征频率虚部 (a)纯的相干型耦合($ G= g{= g}_{{\mathrm{a}}}{= g}_{{\mathrm{b}}} $)的微波透射谱, $ g $= 20 MHz; 纯的耗散型耦合($ G= -{\mathrm{i}}\varGamma = -{\mathrm{i}}{\varGamma }_{{\mathrm{a}}}= -{\mathrm{i}}{\varGamma }_{{\mathrm{b}}} $), (b) $ \varGamma $= 20 MHz, (c) $ \varGamma $= 45 MHz, 红色和蓝色虚线箭头给出了两个零阻尼点的位置; (d)—(f)为微波透射谱中零阻尼点的微波透射系数与频率失谐$ {\varDelta }_{{\mathrm{c}}} $的变化关系; (g)—(i) 分别给出了(a)—(c)对应的本征频率虚部与频率失谐$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $的变化关系
Figure 3. Microwave transmission spectra and imaginary parts of eigenfrequency for two magnon modes with pure coupling: (a) Microwave transmission spectra of pure coherent coupling ($ G= g{= g}_{{\mathrm{a}}}{= g}_{{\mathrm{b}}} $) with $ g $= 20 MHz, and pure dissipative coupling ($ G= -{\mathrm{i}}\varGamma = -{\mathrm{i}}{\varGamma }_{{\mathrm{a}}}= -{\mathrm{i}}{\varGamma }_{{\mathrm{b}}} $) with (b) $ \varGamma $= 20 MHz and (c) $ \varGamma $= 45 MHz; red and blue dashed arrows denote the positions of two zero damping conditions; (d)–(f) microwave transmission as function of detuning $ {\varDelta }_{{\mathrm{c}}} $ at zero damping conditions; (g)–(i) imaginary parts of eigenfrequency as function of detuning $ {\varDelta }_{mc} $ for each coupling in (a)–(c).
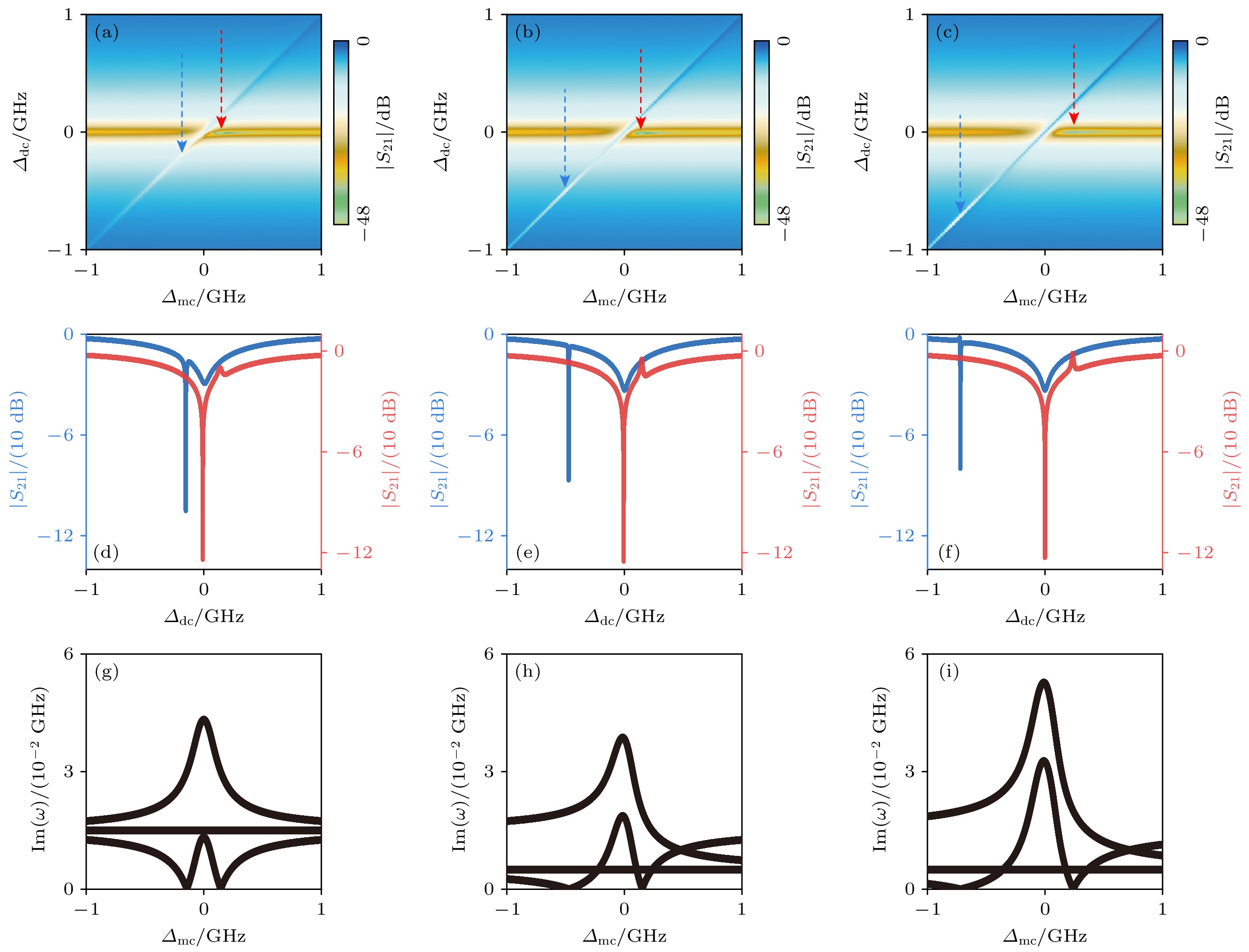
图 4 两个磁子模式在混合型耦合(相干型耦合和耗散型耦合同时存在)下的微波透射谱与本征频率虚部 (a)耦合强度$ G= (30-20{\mathrm{i}}) $ MHz, 耗散率$ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= {\kappa }_{{\mathrm{c}}}= 15 $ MHz; (b), (a)相同, 但是磁子耗散率$ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= $30 MHz; (c)耦合强度$ G= (30- $$ 30{\mathrm{i}}) $ MHz, 耗散率$ {\kappa }_{{\mathrm{c}}}= 15 $ MHz, $ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= $30 MHz; (d)—(f)微波透射谱中零阻尼点的微波透射系数与频率失谐$ {\varDelta }_{{\mathrm{c}}} $的变化关系; (g)—(i) 分别给出了(a)—(c)对应的本征频率虚部与频率失谐$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $的变化关系
Figure 4. Microwave transmission spectra and imaginary parts of eigenfrequency for two magnon mode with both coherent and dissipative couplings present: (a) Coupling strength $ G= (30-20{\mathrm{i}}) $ MHz and damping rate $ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= {\kappa }_{{\mathrm{c}}}= 15 $ MHz; (b) the same as (a) but with $ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= $30 MHz; (c) coupling strength $ G= (30-30{\mathrm{i}}) $ MHz and damping rate $ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= 30 $ MHz and $ {\kappa }_{{\mathrm{c}}}= 15 $ MHz; (d)–(f) microwave transmission as function of detuning $ {\varDelta }_{{\mathrm{c}}} $ at zero damping conditions; (g)–(i) imaginary parts of eigenfrequency as function of detuning $ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $ for each coupling in (a)–(c).
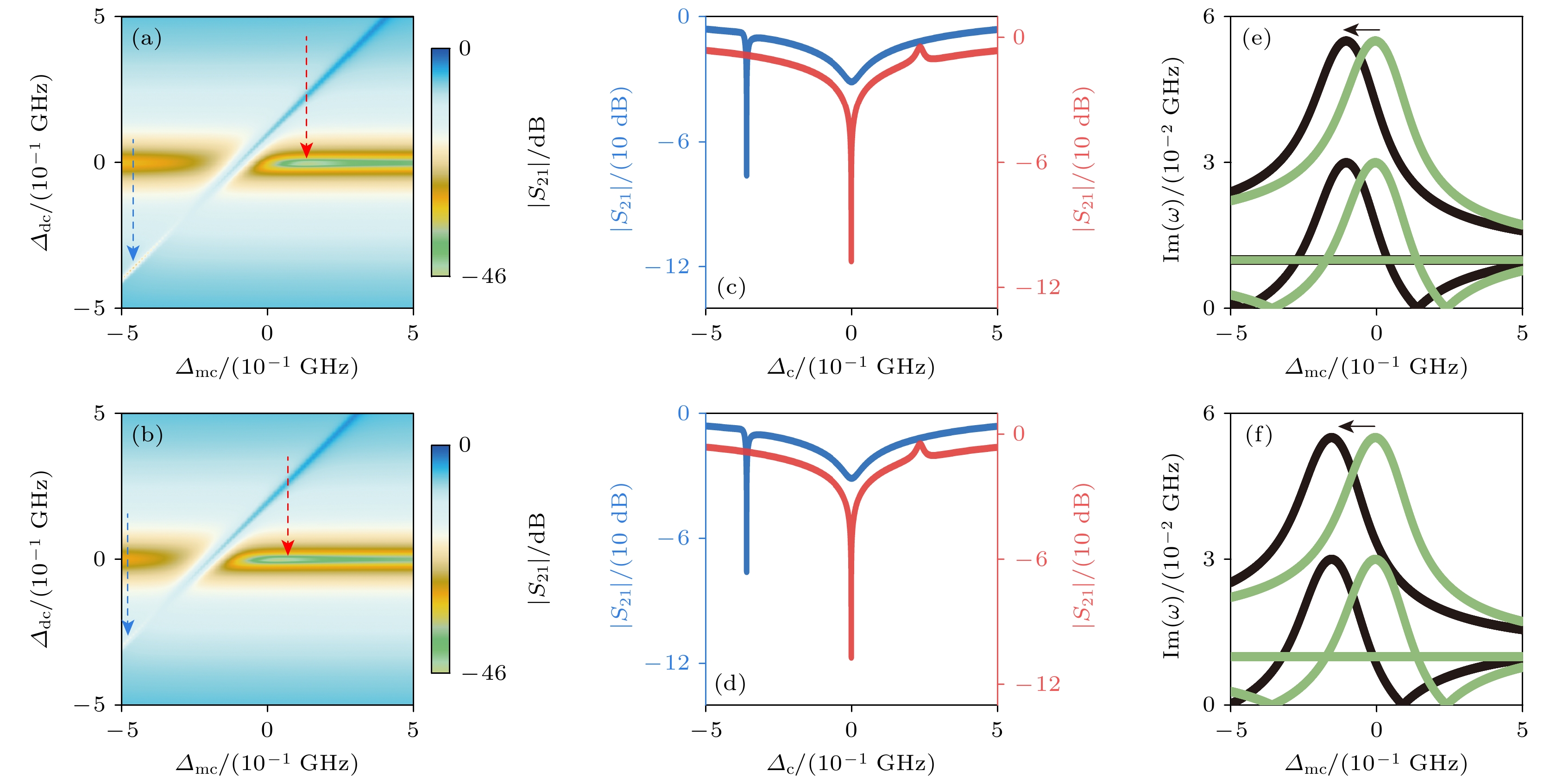
图 5 两个磁子模式在不同层间耦合强度下的微波透射谱与本征频率虚部 (a) $ {g}_{{\mathrm{a}}{\mathrm{b}}}= $ 100 MHz, (b) $ {g}_{{\mathrm{a}}{\mathrm{b}}}= $ 200 MHz, 耦合强度均为$ G= (30-30{\mathrm{i}}) $ MHz; (c), (d)为微波透射谱中零阻尼点的微波透射系数与频率失谐$ {\varDelta }_{{\mathrm{c}}} $的变化关系; (e), (f) 分别给出了(a), (b)对应的本征频率虚部与频率失谐$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $的变化关系, 绿色曲线代表$ {g}_{{\mathrm{a}}{\mathrm{b}}}= 0 $的结果
Figure 5. Microwave transmission spectra and imaginary parts of eigenfrequency for two magnon mode with interlay coupling present: (a) Interlayer coupling strength $ {g}_{{\mathrm{a}}{\mathrm{b}}}= $ 100 MHz, (b) $ {g}_{{\mathrm{a}}{\mathrm{b}}}= $ 200 MHz, photon-magnon coupling strength is $ G= (30-30{\mathrm{i}}) $ MHz; (c), (d) microwave transmission as function of detuning $ {\varDelta }_{{\mathrm{c}}} $ at zero damping conditions; (e), (f) imaginary parts of eigenfrequency as function of detuning $ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $ for each coupling in (a), (b), the green curves represent the results of $ {g}_{{\mathrm{a}}{\mathrm{b}}}= 0 $.
-
[1] Zhang X F, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401
 Google Scholar
Google Scholar
[2] Soykal O O, Flatt´e M E 2010 Phys. Rev. Lett. 104 077202
 Google Scholar
Google Scholar
[3] Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2015 Science 349 405
 Google Scholar
Google Scholar
[4] Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003
 Google Scholar
Google Scholar
[5] Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603
 Google Scholar
Google Scholar
[6] Goryachev M, Farr W G, Creedon D L, Fan Y, Kostylev M, Tobar M E 2014 Phys. Rev. Appl. 2 054002
 Google Scholar
Google Scholar
[7] Cao Y, Yan P, Huebl H, Goennenwein S T B, Bauer G E W 2015 Phys. Rev. B 91 094423
 Google Scholar
Google Scholar
[8] Bai L, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201
 Google Scholar
Google Scholar
[9] Bernier N R, T´oth L D, Feofanov A K, Kippenberg T J 2018 Phys. Rev. A 98 023841
 Google Scholar
Google Scholar
[10] Yu W C, Wang J J, Yuan H Y, Xiao J 2019 Phys. Rev. Lett. 123 227201
 Google Scholar
Google Scholar
[11] Grigoryan V L, Shen K, Xia K 2018 Phys. Rev. B 98 024406
 Google Scholar
Google Scholar
[12] Wu W J, Xu D, Qian J, Li J, Wang Y P, You J Q 2022 Chin. Phys. B 31 127503
 Google Scholar
Google Scholar
[13] Bao X X, Guo G F, Yang X, Tan L 2023 Chin. Phys. B 32 080301
 Google Scholar
Google Scholar
[14] Liao Q, Peng K, Qiu H 2023 Chin. Phys. B 32 054205
 Google Scholar
Google Scholar
[15] Liu T, Zhang X, Tang H X, Flatte M E 2016 Phys. Rev. B 94 060405(R
 Google Scholar
Google Scholar
[16] Zare R B, Viola K S, Haigh J A, Usami K, Lachance-Quirion D, Nakamura Y, Hu C M, Tang H X, Bauer G E, Blanter Y M 2022 Phys. Rep. 979 1
 Google Scholar
Google Scholar
[17] Harder M, Yao B, Gui Y, Hu C M 2021 J. Appl. Phys. 129 201101
 Google Scholar
Google Scholar
[18] Yuan H, Cao Y, Kamra A, Duine R A, Yan P 2022 Phys. Rep. 965 1
 Google Scholar
Google Scholar
[19] Lachance-Quirion D, Tabuchi Y, Gloppe A, Usami K, Nakamura Y 2019 Appl. Phys. Exp. 12 070101
 Google Scholar
Google Scholar
[20] Lachance-Quirion D, Wolski S P, Tabuchi Y, Kono S, Usami K, Nakamura Y 2020 Science 367 425
 Google Scholar
Google Scholar
[21] Pan H, Yang Y, An Z H, Hu C M 2022 Phys. Rev. B 106 054425
 Google Scholar
Google Scholar
[22] Hyde P, Yao B M, Gui Y S, Zhang G Q, You J Q, Hu C M 2018 Phys. Rev. B 98 174423
 Google Scholar
Google Scholar
[23] Bi M X, Yan X H, Xiao Y, Dai C J 2019 J. Appl. Phys. 126 173902
 Google Scholar
Google Scholar
[24] Bi M X, Yan X H, Zhang Y, Xiao Y 2021 Phys. Rev. B 103 104411
 Google Scholar
Google Scholar
[25] Wang Y P, Zhang G Q, Zhang D, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202
 Google Scholar
Google Scholar
[26] Sharma S, Bittencourt V A S V, Karenowska A D, Kusminskiy S V 2021 Phys. Rev. B 103 L100403
 Google Scholar
Google Scholar
[27] Hei X L, Li P B, Pan X F, Nor F 2023 Phys. Rev. Lett. 130 073602
 Google Scholar
Google Scholar
[28] Yuan H Y, Yan P, Zheng S, He Q Y, Xia K, Yung M H 2020 Phys. Rev. Lett. 124 053602
 Google Scholar
Google Scholar
[29] Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601
 Google Scholar
Google Scholar
[30] Yang J Y, Zhao C S, Wang D W, Peng R, Zhou L 2024 Phys. Rev. Appl. 21 044056
 Google Scholar
Google Scholar
[31] Sun F X, Zheng S S, Xiao Y, Gong Q, He Q, Xia K 2021 Phys. Rev. Lett. 127 087203
 Google Scholar
Google Scholar
[32] Osada A, Hisatomi R, Noguchi A, Tabuchi Y, Yamazaki R, Usami K, Sadgrove M, Yalla R, Nomura M, Nakamura Y 2016 Phys. Rev. Lett. 116 223601
 Google Scholar
Google Scholar
[33] Haigh J A, Nunnenkamp A, Ramsay A J, Ferguson A J 2016 Phys. Rev. Lett. 117 133602
 Google Scholar
Google Scholar
[34] Zhang X F, Zhu N, Zou C L, Tang H X 2016 Phys. Rev. Lett. 117 123605
 Google Scholar
Google Scholar
[35] Osada A, Gloppe A, Hisatomi R, Noguchi A, Yamazaki R, Nomura M, Nakamura Y, Usami K 2018 Phys. Rev. Lett. 120 133602
 Google Scholar
Google Scholar
[36] Harder M, Yang Y, Yao B M, Yu C H, Rao J W, Gui Y S, Stamps R L, Hu C M 2018 Phys. Rev. Lett. 121 137203
 Google Scholar
Google Scholar
[37] Yang Y, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2019 Phys. Rev. Appl. 11 054023
 Google Scholar
Google Scholar
[38] Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202
 Google Scholar
Google Scholar
[39] Zhang X F, Zou C, Zhu N, Marquardt F, Jiang L, Tang H X 2015 Nat. Commun. 6 8914
 Google Scholar
Google Scholar
[40] Nair J M P, Mukhopadhyay D, Agarwal G S 2022 Phys. Rev. B 105 214418
 Google Scholar
Google Scholar
[41] Zhang Q, Xue J S, Sun Y T, Guo J J, Chen Y X, Tian Y F, Yan S S, Bai L H 2021 Phys. Rev. B 104 094303
 Google Scholar
Google Scholar
[42] Zhang D S, Song W J, Chai G Z 2017 J. Phys. D: Appl. Phys. 50 205003
 Google Scholar
Google Scholar
[43] An K, Kohno R, Litvinenko A N, Seeger R L, Naletov V V, Vila L, De Loubens G, Youssef J B, Vukadinovic N, Bauer G E W, Slavin A N, Tiberkevich V S, Klein O 2022 Phys. Rev. X 12 011060
[44] Tserkovnyak Y, Brataas A, Bauer G E W, Halperin B I 2005 Rev. Mod. Phys. 77 1375
 Google Scholar
Google Scholar
[45] Ma K, Li C, Hao Z, Ong C K, Chai G 2023 Phys. Rev. B 108 094422
 Google Scholar
Google Scholar
[46] Zhan X X, Zhang Y, Yan X H, Xiao Y 2021 J. Appl. Phys. 130 123901
 Google Scholar
Google Scholar
[47] Mahan G D 2000 Many-Particle Physics (Kluwer Academic/Plenum Publishers
[48] Holstein T, Primakoff H 1940 Phys. Rev. 58 1098
 Google Scholar
Google Scholar
[49] Chen J L, Liu C P, Liu T, Xiao Y, Xia K, Bauer G E W, Wu M Z, Yu H M 2018 Phys. Rev. Lett. 120 217202
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 1351
- PDF Downloads: 56
- Cited By: 0














 DownLoad:
DownLoad: