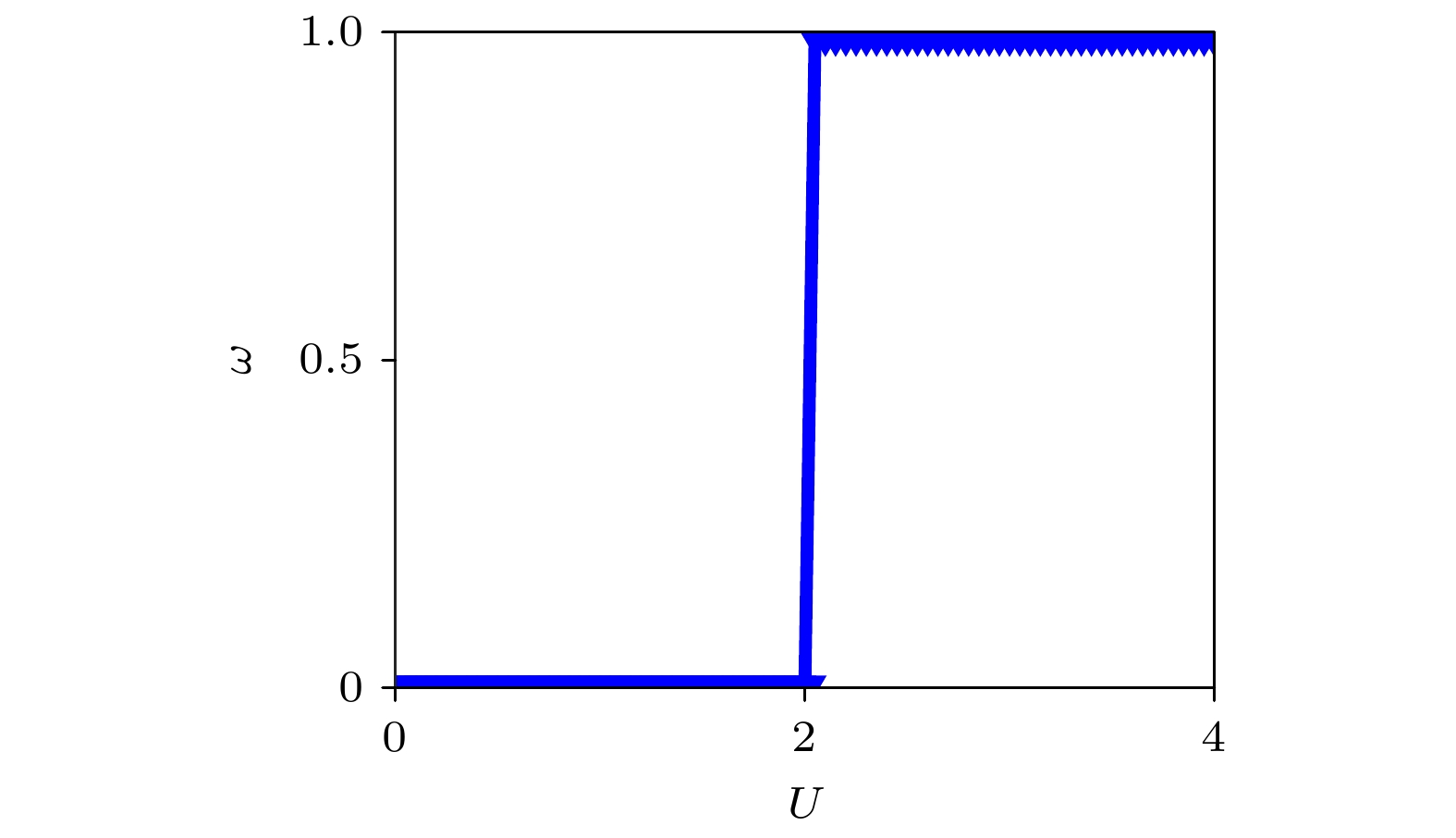
-
In this work, we investigate a one-dimensional two-boson system with complex interaction modulation, described by the Hamiltonian: $\hat{H}=-J\displaystyle\sum\limits_{j}\left(\hat{c}_j^\dagger\hat{c}_{j+1}+h.c\right)+\sum\limits_{j}\frac{U}{2}e^{2i\pi\alpha j}\hat{n}_j\left(\hat{n}_j-1\right), $ where U is the interaction amplitude, and the modulation frequency $\alpha=(\sqrt{5}-1)$ is an irrational number. The interaction satisfies $U_{-j}=U^*_j$, which ensures that the system possesses party-time (PT) reversal symmetry. Using the exact diagonalization method, we numerically calculate the real-to-complex transition of the energy spectrum, Shannon entropy, the normalized participation ration, and the topological winding number. For small U, all eigenvalues are real. However, as U increases, eigenvalues corresponding to two particles occupying the same site become complex, marking a PT symmetry-breaking transition at $U=2$. This point signifies a real-to-complex transition in the spectrum. To characterize the localization properties of the system, we employ the Shannon entropy and the normalized participation ration (NPR). When $U<2$, all the eigenstates are extended, exhibiting high Shannon entropy and NPR values. Conversely, for $U>2$, states with complex eigenvalues show low Shannon entropy and significantly reduced NPR, indicating localization. Meanwhile, states with real eigenvalues remain extended in this regime. We further analyze the topological aspects of the system by using the winding number. A topological phase transition occurs at $U=2$, where the winding number changes from 0 to 1. This transition coincides with the onset of $PT$ symmetry breaking and the localization transition. The dynamical evolution can be used to detect the localization properties and the real-to-complex transition, with the initial state being two bosons occupying the center site of the chain simultaneously. Finally, we propose an experimental realization by using a two-dimensional linear photonic waveguide array. The modulated interaction can be controlled by adjusting the real part and imaginary part of the refractive index of diagonal waveguide. To simulate this non-Hermitian two-body problem, we numerically calculate the density distribution of the wave packet in a two-dimensional plane, which indirectly reflects the propagation of light in a two-dimensional waveguide array. We hope that our work can deepen the understanding of the relation between interaction and disorder while arousing further interest in two-body systems and non-Hermitian localization. -
Keywords:
- non-Hermitian /
- localization /
- topology /
- PT symmetry
-
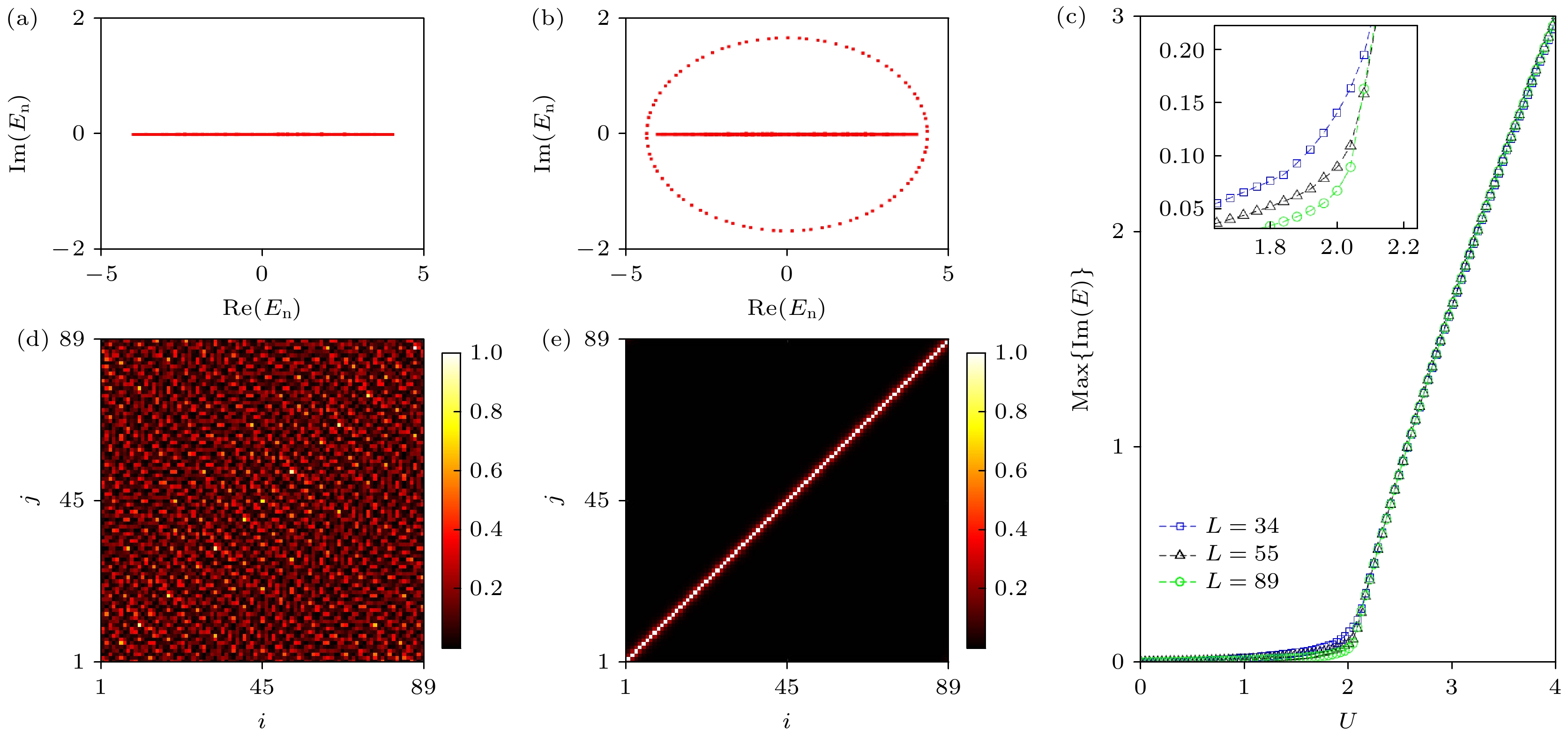
图 1 系统的能谱: (a)$ U=1 $, (b)$ U=3 $. (c)不同尺寸下能量虚部的绝对值的最大值随U的变化. (d)在$ U=1 $ 时, 能量虚部最大值所对应本征态的两玻色子的坐标关联. (e)在$ U=3 $时, 复能量环上两玻色子的坐标关联
Figure 1. The complex energy spectrum for (a)$ U=1 $ and (b)$ U=3 $, respectively. (c) The maximum value of the absolute value of the imaginary part of energy as a function of U for different L. (d)The coordinate correlation of two bosons corresponding to the eigenstate with the maximum value of the imaginary part of energy for $ U=1 $. (e)The coordinate correlation of two bosons on the complex energy ring for $ U=3 $.
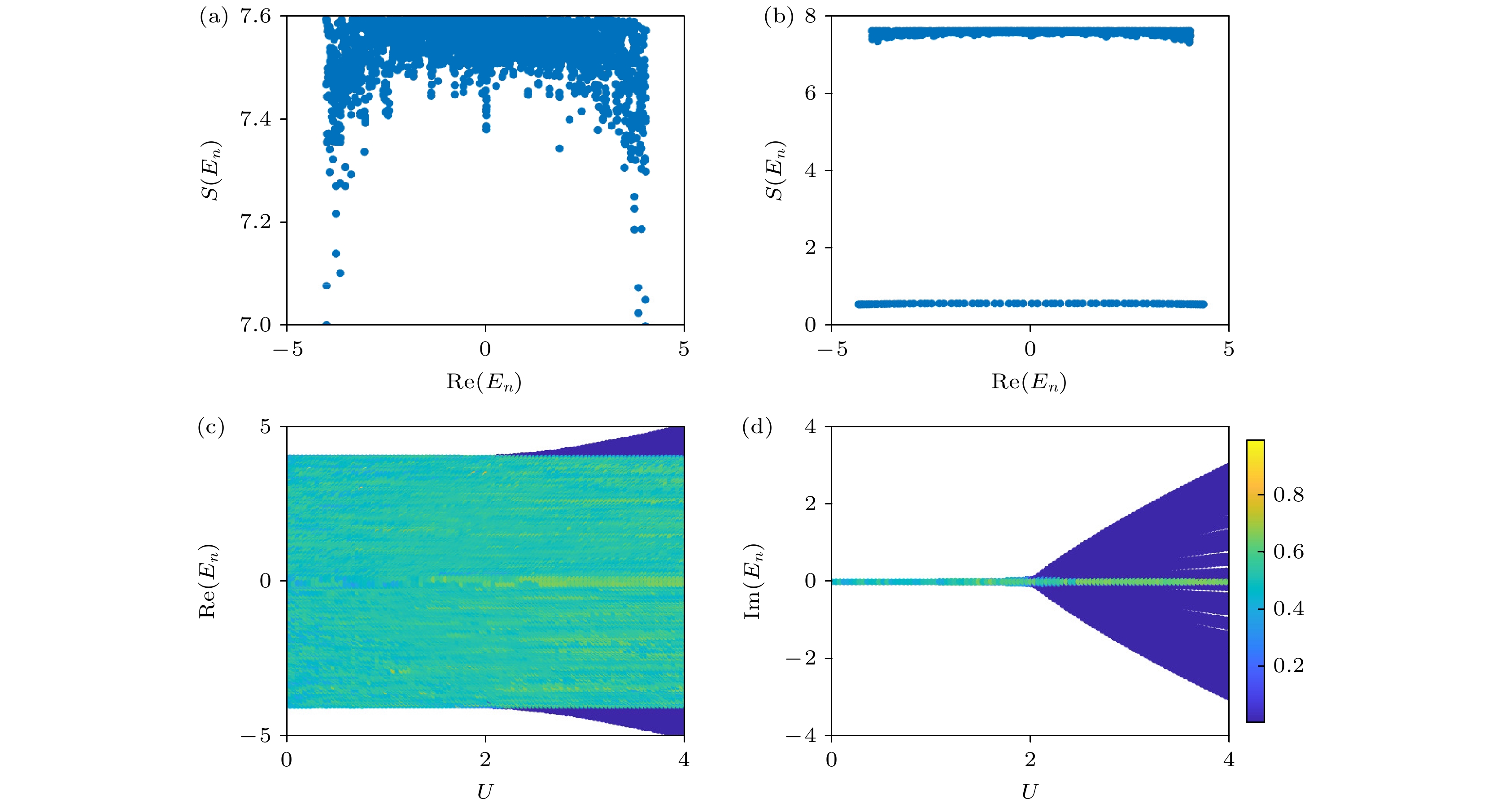
图 2 系统的Shannon熵随能量本征值的变化: (a)$ U=1 $, (b)$ U=3 $. (c) $ \eta(E) $在不同的相互作用U下随能量本征值$ E_n $的实部的变化. (d) $ \eta(E_n) $在不同的相互作用U下随能量本征值$ E_n $的虚部的变化. 这里, $ L=89 $
Figure 2. The Shannon entropy as the function of $ \mathrm{Re}(E_n) $ for (a) $ U=1 $ and (b) $ U=3 $, respectively. (c) $ \eta(E_n) $ as the function of $ \mathrm{Re}(E_n) $. (d) $ \eta(E_n) $ as the function of $ \mathrm{Im}(E_n) $. Here, $ L=89 $.
图 3 缠绕数ω随相互作用强度U变化的图像.
Figure 3. The winding number ω as a function of U.
图 4 坐标空间下两玻色子系统的密度演化: (a)$ U=1 $, (b)$ U=3 $. (c)$ U=3 $时, $ P\left(t\right) $随时间的演化. 这里, $ L=89 $
Figure 4. The density evolution of a two-boson system in position space with (a)$ U=1 $ and (b)$ U=3 $, respectively. (c) The time evolution of $ P\left(t\right) $ for $ U=3 $. Here, $ L=89 $.
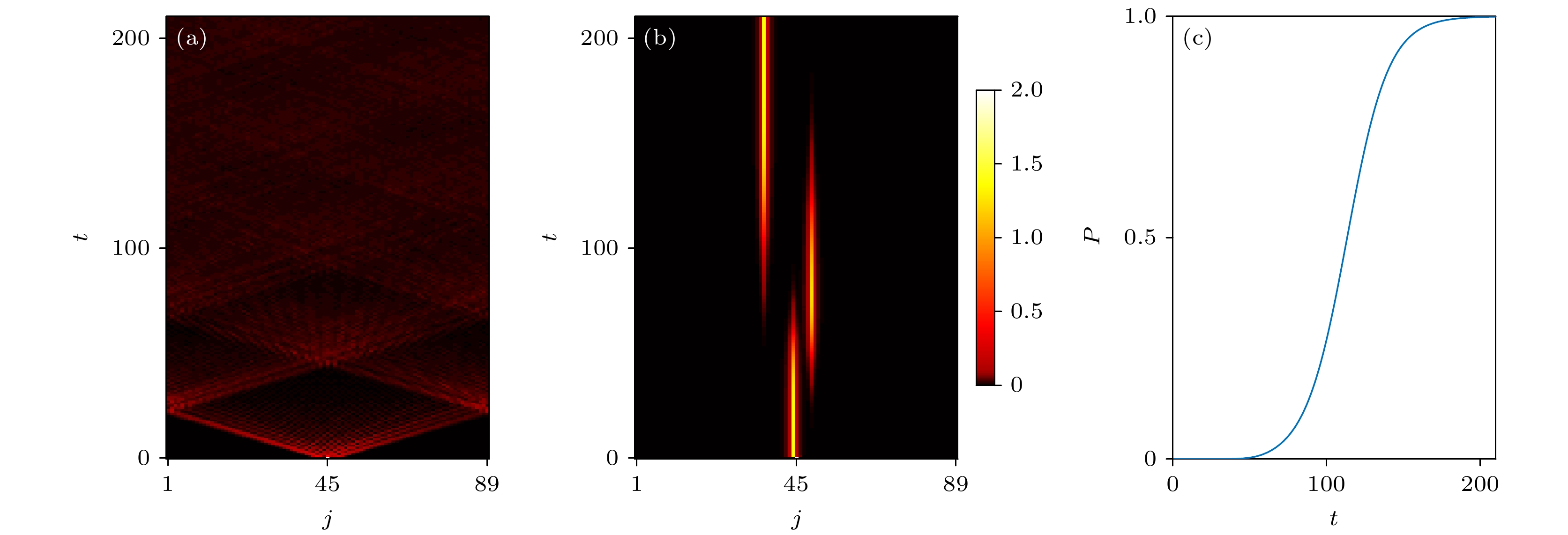
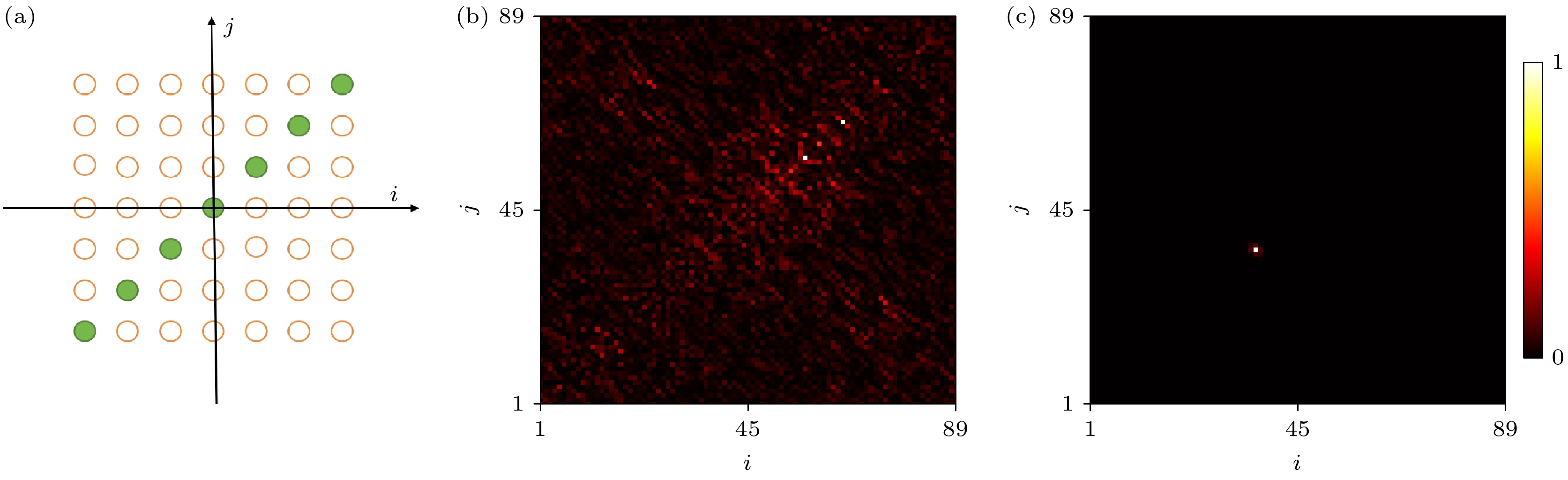
图 5 (a) 二维光子波导阵列的示意图. 每个圆圈代表一个波导. 橘黄色空圆圈和绿色圆圈分别标示具有不同折射率的波导, 从而有效地实现复调制的在位相互作用. 这个二维几何结构关于对角线对称. $ t=200 $时刻粒子在二维平面内的密度扩散: (b) $ U=1 $ (c) $ U=3 $
Figure 5. Schematic diagram of the two-dimensional linear photonic waveguide array. Each circle represents a waveguide. Orange-yellow hollow and green-colored circles label waveguides with different refractive indices, which can effectively control the complex modulated on-site interactions. This two-dimensional geometric structure is symmetric with respect to the diagonal. The density distributions of the wave packets in the 2 D plane at time $ t = 200 $ for (b) $ U=1 $ (c)$ U=3 $, respectively.
-
[1] Anderson, P W 1958 Phys. Rev. 109 1492
Google Scholar
[2] Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891
Google Scholar
[3] Roati G, D'Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895
Google Scholar
[4] Chabanov A A, Stoytchev M, Genack A Z 2000 Nature 404 850
Google Scholar
[5] Pradhan P, Sridhar S 2000 Phys. Rev. Lett. 85 2360
Google Scholar
[6] Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Silberberg Y 2009 Phys. Rev. Lett. 103 013901
Google Scholar
[7] 徐志浩, 皇甫宏丽, 张云波 2005 68 222
Xu Z H, Huang F H L, Zhang Y B 2005 Acta Phys. Sin. 68 222
[8] Bender, Carl M, Stefan Boettcher 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[9] W. D. Heiss, 2012 Phys. Rev. A 45 444016
[10] M.-A. Miri, A. Alù 2019 Science. 363 086803
[11] Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802
Google Scholar
[12] Ou Z, Wang Y, Li L 2023 Phys. Rev. B 107 L161404
Google Scholar
[13] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[14] Borgnia D S, Kruchkov A J, Slager R J 2020 Phys. Rev. Lett. 124 056802
Google Scholar
[15] J. Feinberg and A. Zee, 1999 Phys. Rev. E 59 6433
Google Scholar
[16] K. Kawabata, K. Shiozaki, M. Ueda, and M. Sato 2019 Phys. Rev. X 9 041015
[17] Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570
Google Scholar
[18] Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651
Google Scholar
[19] Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384
Google Scholar
[20] Longhi, Stefano 2019 Phys. Rev. B 100 125157
Google Scholar
[21] Hamazaki R, Kawabata K, Ueda M 2019 Phys. Rev. Lett. 123 090603
Google Scholar
[22] Zhai L J, Yin S, Huang G Y 2020 Phys. Rev. B 102 064206
Google Scholar
[23] Liu J H, Xu Z H 2023 Phys. Rev. B 108 184205
Google Scholar
[24] Tomita T, Nakajima S, Danshita I, Takasu Y, Takahashi Y 2017 Sci. Adv. 3 e1701513
Google Scholar
[25] Sponselee K, Freystatzky L, Abeln B, et al 2018 Quantum Sci. Technol 4 0140027
[26] Lee C H 2021 Phys. Rev. B 104 195102
Google Scholar
[27] Shen R, Lee C H 2022 Communications Physics 5 238
Google Scholar
[28] M Gao, C Sheng, Y Zhao, R He, et al 2024 Phys. Rev. B 110 094308
Google Scholar
[29] G Corrielli, A Crespi, G Della Valle, S Longhi, R Osellame 2013 Nature communications 4 1555
Google Scholar
[30] Yan Xing, Xuedong Zhao, Zhe Lü, et al 2021 Optics Expres 29 40428
Google Scholar
[31] Wang Y C, Hu H P, Chen S 2016 Eur. Phys. J B 89 1
Google Scholar
[32] Zhou L W. Han, W Q 2021 Chin. Phys. B 30 100308
Google Scholar
[33] Tian Q, Gu Y J, Zhou L W 2024 Phys. Rev. B 109 054204
DownLoad:
Metrics
- Abstract views: 255
- PDF Downloads: 5
- Cited By: 0
