-
Acoustic skyrmion modes are topological texture structures of velocity field vectors generated on the surface of acoustic structures. This protected vector distribution provides new dimensions for processing advanced sound information, transmission, and data storage. In this study, a combined structure of waveguides and spiral structures is designed by using directional acoustic sources to excite waveguide mode transmission, thereby achieving selective excitation of localized acoustic skyrmion modes. Through theoretical analysis and numerical simulations, the pressure field distribution and velocity field distribution excited by spin acoustic sources, Huygens acoustic sources, and Janus acoustic sources in this structure are investigated, demonstrating the directional transmission properties of acoustic surface waves and the selectively excited acoustic skyrmion modes in the combined structure. Numerical calculations reveal that when the spin acoustic source excites acoustic surface waves propagating along the waveguide, the acoustic skyrmion modes in the helical structure in the direction corresponding to the propagation are selectively excited. When the Huygens source excites acoustic surface waves propagating along the waveguide, the acoustic skyrmion modes in the right or left direction are selectively excited. However, when the Janus source excites acoustic surface waves propagating along the waveguide, the acoustic skyrmion modes in the upward or downward direction are selectively excited. This waveguide excitation method is a new means of exciting acoustic skyrmion modes, making the excitation of acoustic skyrmion modes more flexible. Moreover, this waveguide excitation method has significant potential applications in more complex and larger-scale acoustic systems. The research results may promote the understanding of the symmetry in acoustic near-field physics, open up new ways for manipulating particles by using sound waves, and also pave the way for designing advanced acoustic devices.
-
图 1 (a) 组合结构示意图; (b) 不同波导宽度$ {\mathrm{Q}}{\mathrm{U}}{\mathrm{O}}{\mathrm{T}}{\mathrm{E}}{\mathrm{W}}{\mathrm{W}} $的色散关系曲线; (c)螺旋结构示意图; (d) 声学斯格明子模式图
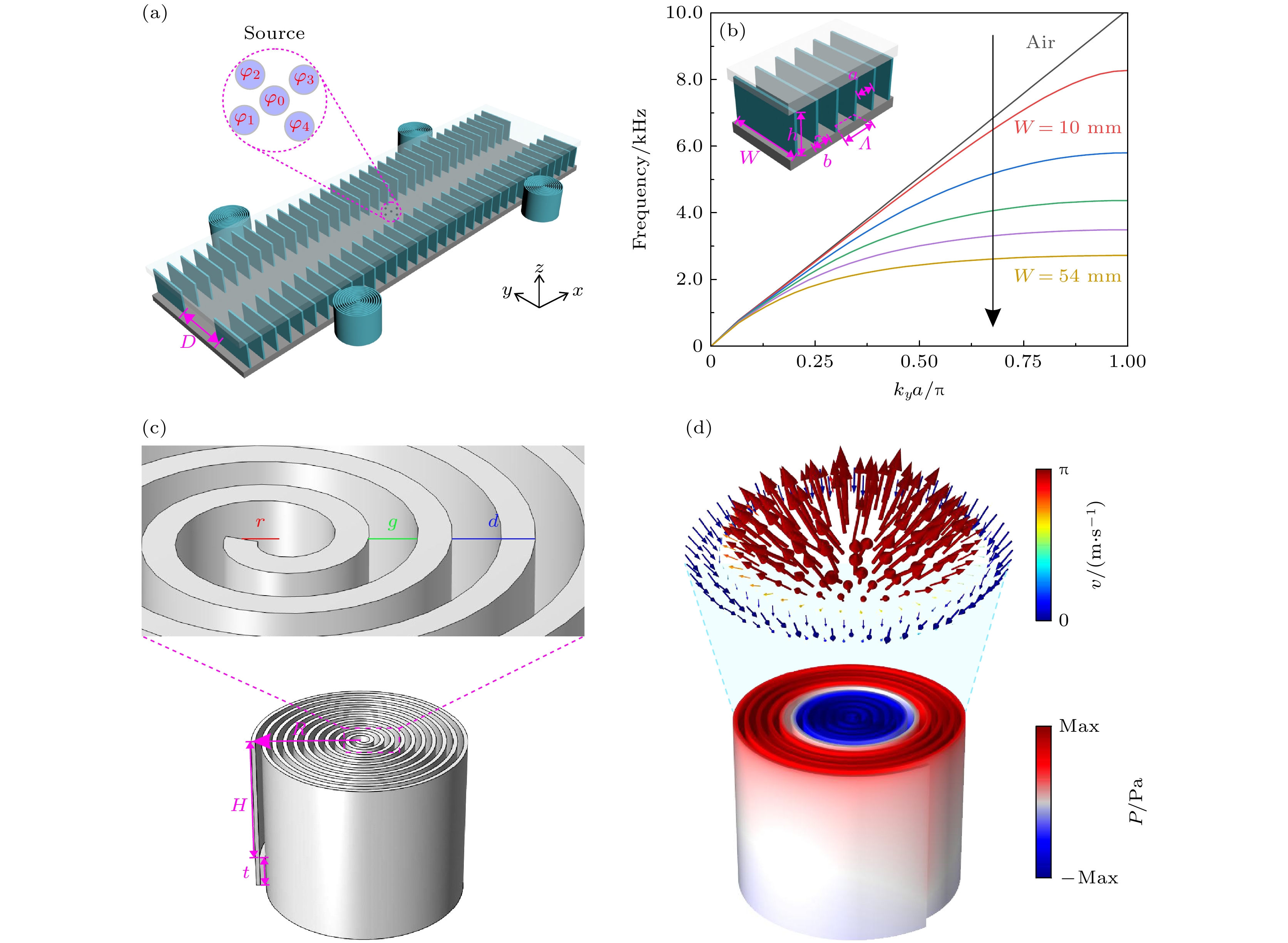
Figure 1. (a) Schematic diagram of combination structure; (b) dispersion relation curves for different waveguide widths $ W $; (c) schematic diagram of spiral structure; (d) acoustic skyrmion pattern diagram.
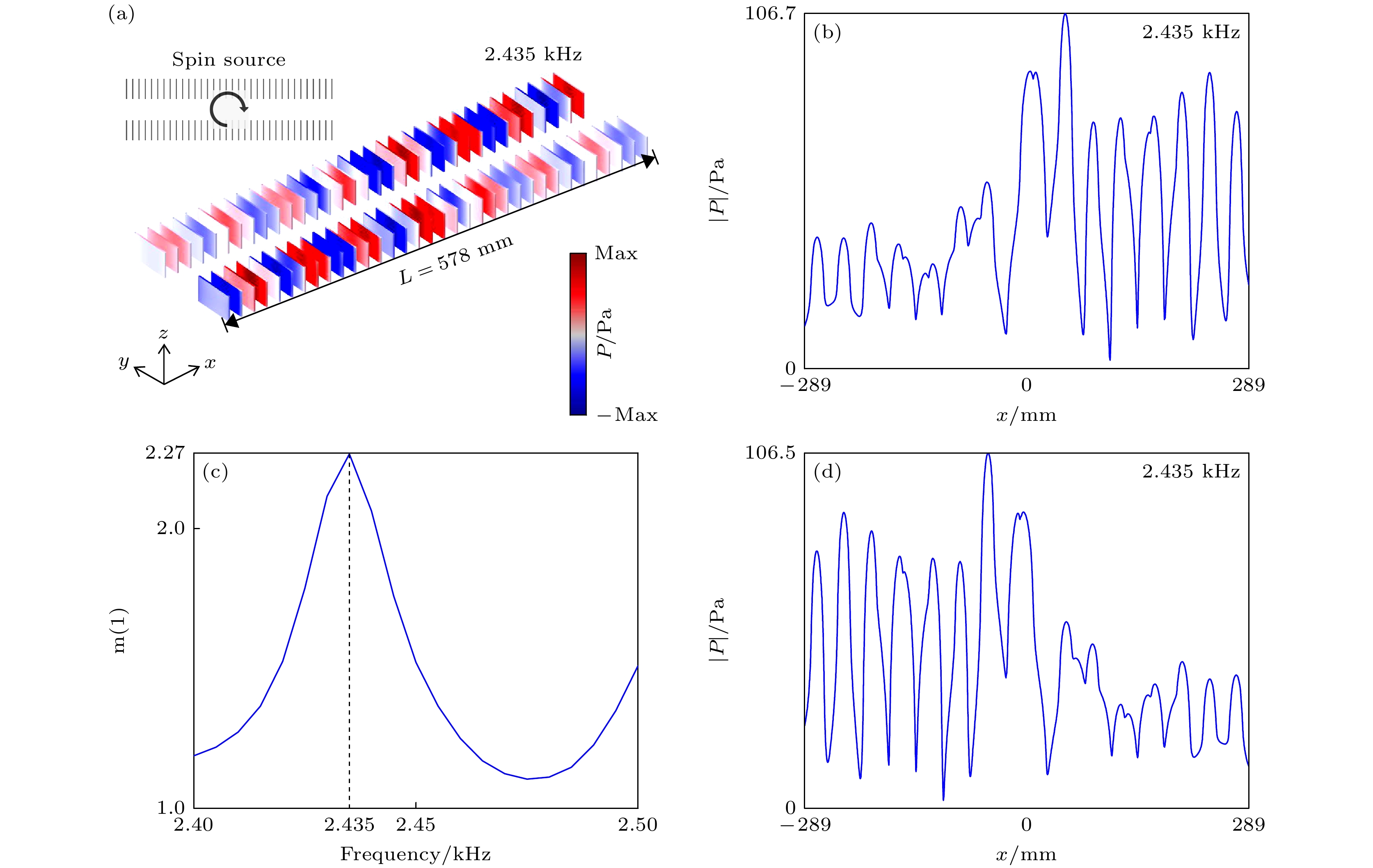
图 2 (a) 顺时针旋转的自旋声源激发声表面波沿波导定向传播示意图; (b) 声表面波沿上方波导向右传播的声压强度变化曲线图; (c) 声表面波沿波导前后向传输比随频率变化的曲线图; (d) 声表面波沿下方波导向左传播的声压强度变化曲线图
Figure 2. (a) Schematic diagram of the directional propagation of surface acoustic waves along a waveguide excited by a clockwise rotating spin acoustic source; (b) graph of the variation of sound pressure intensity of surface acoustic waves propagating to the right along the upper waveguide; (c) graph of the ratio of forward and backward transmission of surface acoustic waves along the waveguide as a function of frequency; (d) graph of the variation in sound pressure intensity of surface acoustic waves propagating to the left along the lower waveguide.
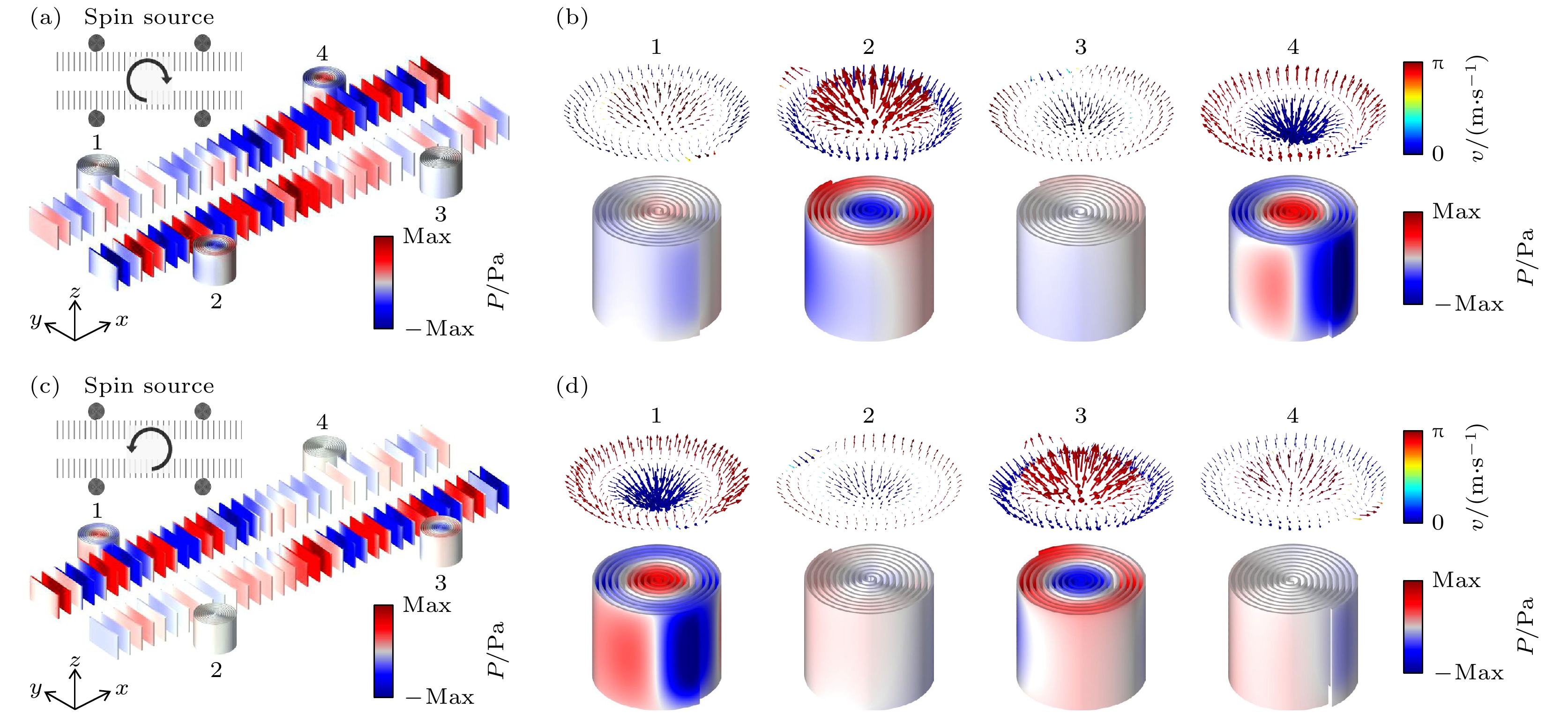
图 3 (a) 顺时针旋转的自旋声源激发的组合结构中压力场分布; (b) 顺时针旋转的自旋声源激发的组合结构中的声学斯格明子模式; (c) 逆时针旋转的自旋声源激发的组合结构中的压力场分布; (d) 逆时针旋转的自旋声源激发的组合结构中的声学斯格明子模式
Figure 3. (a) Pressure field distribution in a combined structure excited by a clockwise rotating spin source; (b) acoustic skyrmion modes in combinatorial structures excited by clockwise rotating spin sources; (c) pressure field distribution in a combined structure excited by a counterclockwise rotating spin source; (d) acoustic skyrmion modes in combinatorial structures excited by counterclockwise rotating spin sources.
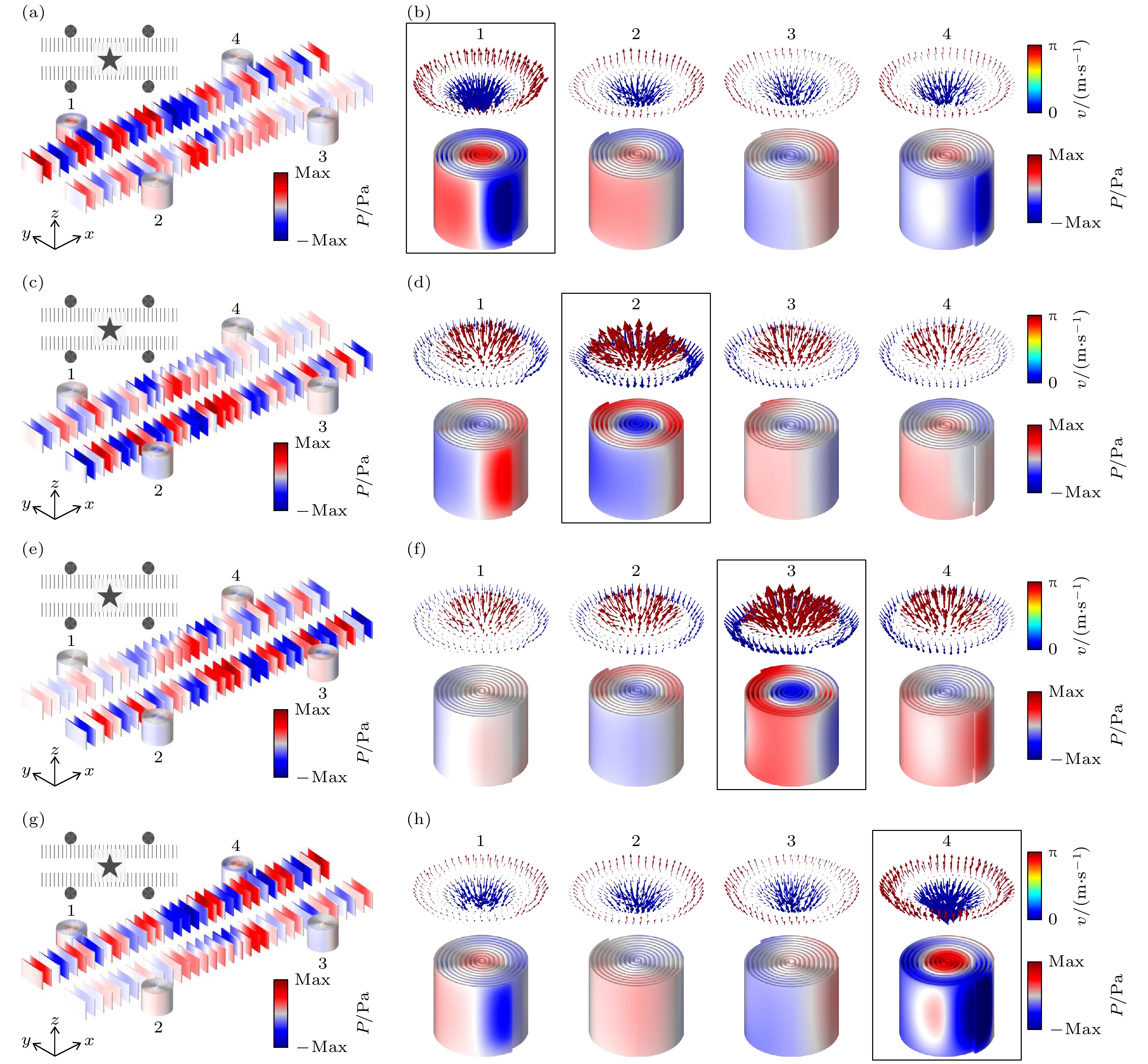
图 4 (a) 声学表面波沿波导向1号方向传播的示意图; (b) 螺旋结构中的声学斯格明子模式; (c) 声学表面波沿波导向2号方向传播; (d) 螺旋结构中的声学斯格明子模式; (e) 声学表面波沿波导向3号方向传播; (f) 螺旋结构中的声学斯格明子模式; (g) 声学表面波沿波导向4号方向传播; (h) 螺旋结构中的声学斯格明子模式
Figure 4. (a) Schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.1; (b) acoustic skyrmion modes in helical structures; (c) schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.2; (d) acoustic skyrmion modes in helical structures; (e) schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.3; (f) acoustic skyrmion modes in helical structures; (g) schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.4; (h) acoustic skyrmion modes in helical structures.
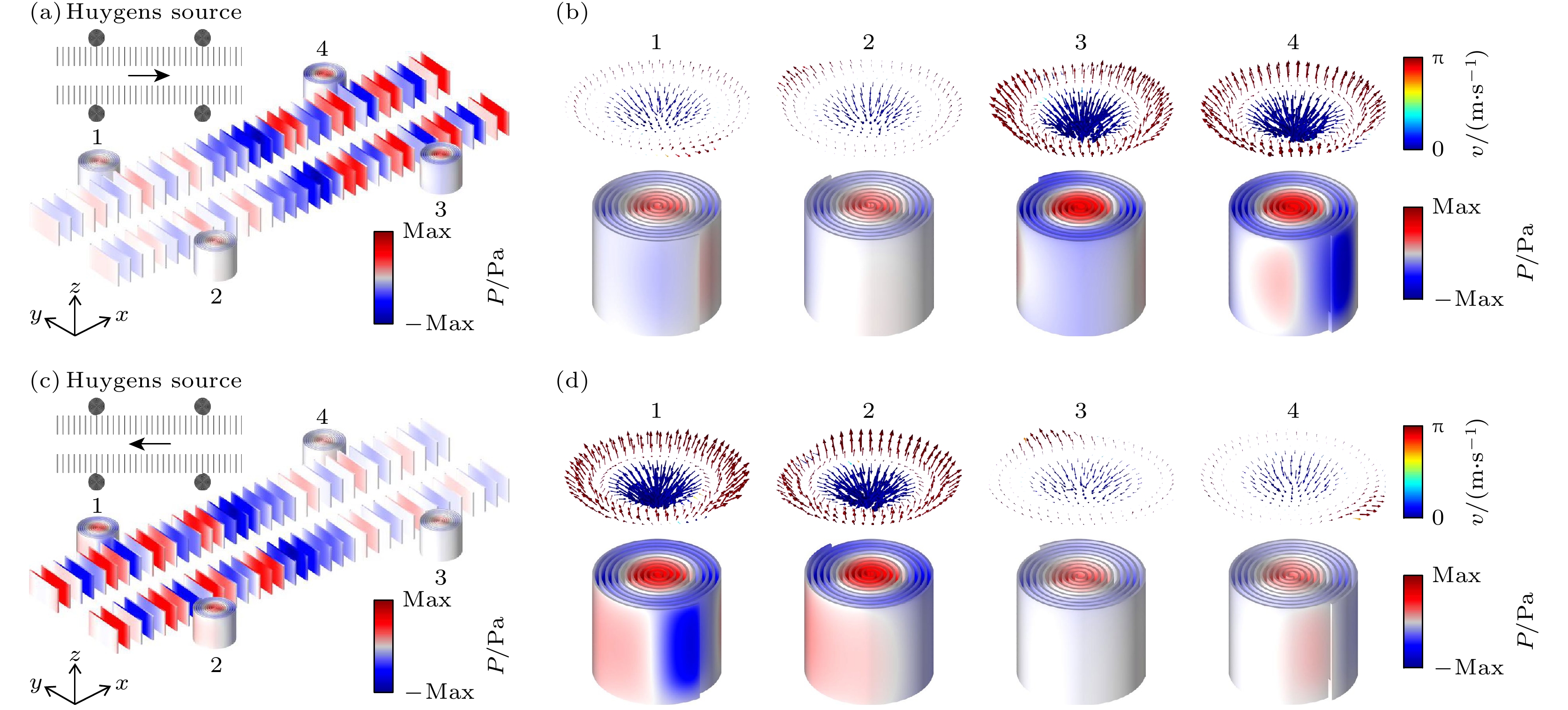
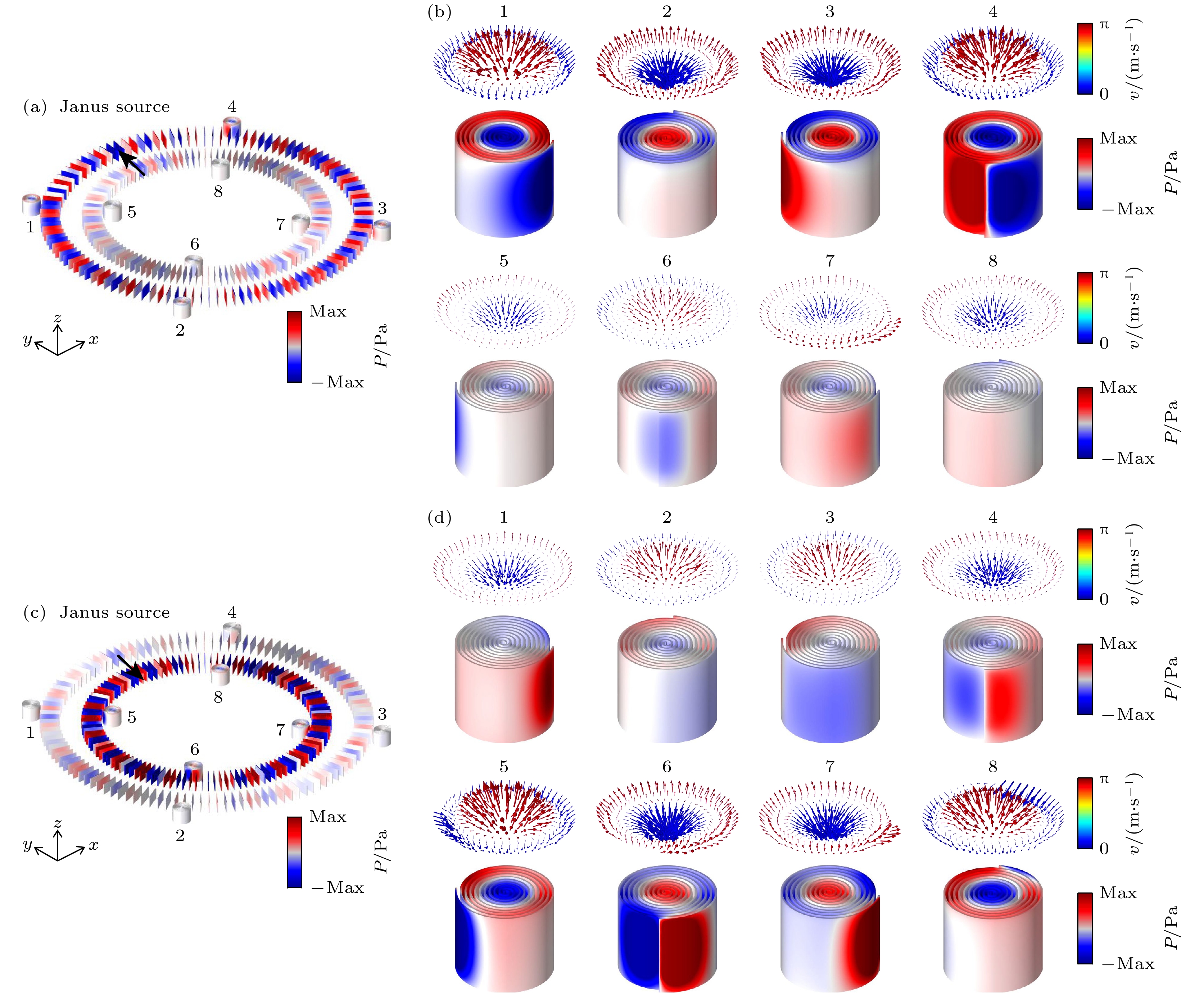
图 5 (a) 前向的Huygens声源激发的组合结构中的压力场分布; (b) 前向的Huygens声源激发的组合结构中的声学斯格明子模式; (c) 后向的Huygens声源激发的组合结构中的压力场分布; (d) 后向的Huygens声源激发的组合结构中的声学斯格明子模式
Figure 5. (a) Pressure field distribution in the combined structure excited by a forward Huygens sound source; (b) acoustic skyrmion modes in the composite structure excited by forward Huygens sound sources; (c) pressure field distribution in the combined structure excited by a backward Huygens sound source; (d) acoustic skyrmion modes in composite structures excited by backward Huygens acoustic sources.
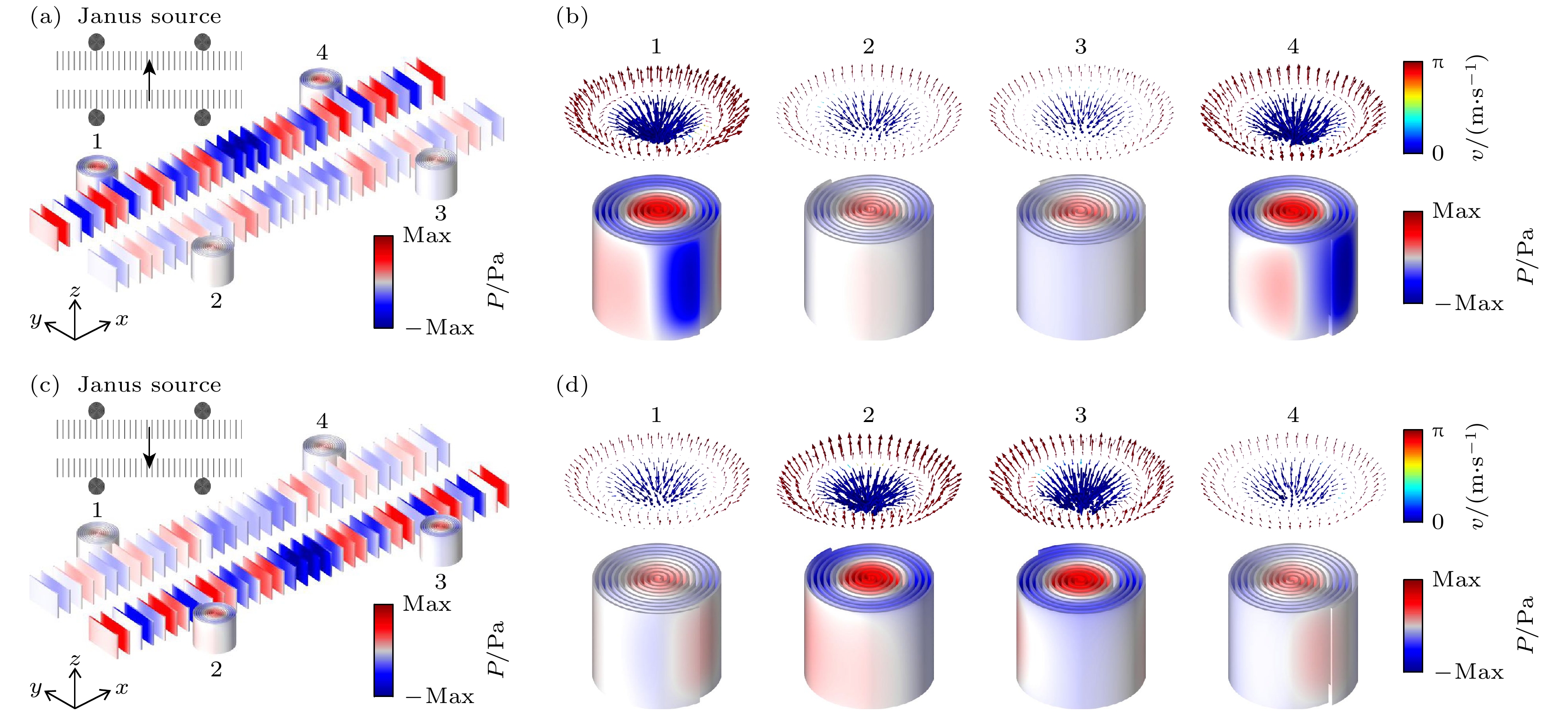
图 6 (a) 向上的Janus声源激发的组合结构中的压力场分布; (b) 向上的Janus声源激发的组合结构中的声学斯格明子模式; (c) 向下的Janus声源激发的组合结构中的压力场分布; (d) 向下的Janus声源激发的组合结构中的声学斯格明子模式
Figure 6. (a) Pressure field distribution in a combined structure excited by an upward Janus source; (b) acoustic skyrmion modes in combinatorial structures excited by upward Janus sources; (c) pressure field distribution in a combined structure excited by a downward Janus source; (d) acoustic skyrmion modes in combinatorial structures excited by downward Janus sources.
图 7 (a) 向上的Janus声源激发的组合结构中的压力场分布; (b) 向上的Janus声源激发的组合结构中的声学斯格明子模式; (c) 向下的Janus声源激发的组合结构中的压力场分布; (d) 向下的Janus声源激发的组合结构中的声学斯格明子模式
Figure 7. (a) Pressure field distribution in a combined structure excited by an upward Janus source; (b) acoustic skyrmion modes in combinatorial structures excited by upward Janus sources; (c) pressure field distribution in a combined structure excited by a downward Janus source; (d) acoustic skyrmion modes in combinatorial structures excited by downward Janus sources.
-
[1] Skyrme T H R 1962 Nucl. Phys. 31 556
Google Scholar
[2] Adkins G S, Nappi C R, Witten E 1983 Nucl. Phys. 228 3
[3] Khawaja U AI, Stoof H 2001 Nature 411 918
Google Scholar
[4] Su S W, Liu I K, Tsai Y C, Liu W M, Gou S C 2012 Phys. Rev. A 86 023601
Google Scholar
[5] Fukuda J I, Zumer S 2011 Nat. Commun 2 246
Google Scholar
[6] Duzgun A, Selinger J, Saxena A 2018 Phys. Rev. E 97 062706
Google Scholar
[7] Robler U K, Bogdanov A N, Pfleiderer C 2006 Nature 442 7104
[8] Tokura Y, Kanazawa N 2021 Chem. Rev. 121 5
[9] Muhlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, Georgii R, Boni P 2009 Science 323 5916
[10] Yu X Z, Koshibae W, Tokunaga Y, Shibata K, Taguchi Y, Nagaosa N, Tokura Y 2018 Nature 564 95
Google Scholar
[11] 陈崇, 马铭远, 潘峰, 宋成 2024 73 5
Chen C, Ma M Y, Pan F, Song C 2024 Acta Phys. Sin. 73 5
[12] Zhang X C, Xia J, Zhou Y, Wang D W, Liu X X, Zhao W S, Ezawa M 2016 Phys. Rev. B 94 094420
Google Scholar
[13] Zhang S L, Kronast F, Van der Laan G, Hesjedal T 2018 Nano Lett. 18 2
[14] Bhukta M M M, Mishra A, Pradhan G, Mallick S, Singh B B, Bedanta S 2018 arXiv 1810: 08262
[15] Kezsmarki I, Bordacs S, Milde P, Neuber E, Eng L M, White J S, Ronnow H M, Dewhurst C D, Mochizuki M, Yanai K, Nakamura H, Ehlers D, Tsurkan V, Loidl A 2015 Nat. Mater. 14 1116
Google Scholar
[16] Nayak A K, Kumar V, Ma T, Werner P, Pippel E, Sahoo R, Damay F, Robler U K, Felser C, Parkin S S P 2017 Nature 548 561
Google Scholar
[17] Gilbert D A, Maranville B B, Balk A L, Kirby B J, Fischer P, Pierce D T, Unguris J, Borchers J A, Liu K 2015 Nat. Commun. 6 8462
Google Scholar
[18] Xia J, Zhang X C, Ezawa M, Tretiakov O A, Hou Z P, Wang W H, Zhao G P, Liu X X, Diep H T, Zhou Y 2020 Appl. Phys. Lett. 117 012403
Google Scholar
[19] Nagaosa N, Tokura Y 2013 Nat. Nanotechnol. 8 899
Google Scholar
[20] Fert A, Reyren N, Cros V 2017 Nat. Rev. Mater. 2 17031
Google Scholar
[21] Du L P, Yang A P, Zayats A V, Yuan X C 2019 Nat. Phys. 15 650
Google Scholar
[22] Davis T J, Janoschka D, Dreher P, Frank B, Meyer zu Heringdorf F J, Giessen H 2020 Science 368 6489
[23] Tsesses S, Ostrovsky E, Cohen K, Gjonaj B, Lindner N H, Bartal G 2018 Science 361 6406
[24] Bai C Y, Chen J, Zhang Y X, Zhang D W 2020 Opt. Express 28 10320
Google Scholar
[25] Bliokh K Y, Rodriguez-Fortuno F J, Nori F, Zayats A V 2015 Nat. Photonics 9 796
Google Scholar
[26] Shi P, Du L P, Yuan X C 2020 Nanophotonics 9 4619
Google Scholar
[27] Karnieli A, Tsesses S, Bartal G, Arie A 2021 Nat. Commun. 12 1092
Google Scholar
[28] Deng Z L, Shi T, Krasnok A, Li X P, Alu A 2022 Nat. Commun. 13 1
[29] Li X H, Liu L L, Zhou Z X, Shen J R, Zhang Y R, Han G D, Li Z 2022 Adv. Opt. Mater. 10 15
[30] Shi C Z, Zhao R K, Long Y, Yang S, Wang Y, Chen H, Ren J, Zhang X 2019 Natl. Sci. Rev 6 4
[31] Burns L, Bliokh K Y, Nori F, Dressel J 2020 New. J. Phys. 22 053050
Google Scholar
[32] Long Y, Zhang D M, Yang C W, Ge J M, Chen H, Ren J 2020 Nat. Commun. 11 4716
Google Scholar
[33] Bliokh K Y, Nori F 2019 Phys. Rev. B 99 020301
[34] Bliokh K Y, Nori F 2019 Phys. Rev. B 99 174310
Google Scholar
[35] Weiner M, Ni X, Alu A, Khanikaev A B 2022 Nat. Commun. 13 6332
Google Scholar
[36] Long Y, Ge H, Zhang D M, Xu X Y, Ren J, Lu M H, Bao M, Chen H, Chen Y F 2020 NSR 7 6
[37] Sun Q L, Peng Y G, Gao F, Li B, Zhu X F 2023 Phys. Rev. Appl. 20 024025
Google Scholar
[38] Ge H, Xu X Y, Liu L, Xu R, Lin Z K, Yu S Y, Bao M, Jiang J H, Lu M H, Chen Y F 2021 Phys. Rev. Lett. 127 144502
Google Scholar
[39] Hu P, Wu H W, Sun W J, Zhou N, Chen X, Yang Y Q, Sheng Z Q 2023 Appl. Phys. Lett. 122 022201
Google Scholar
[40] Cselyuszka N, Secujski M, Engheta N, Crnojevic-Bengin V 2016 New. J. Phys. 18 103006
Google Scholar
[41] Zhu J, Chen Y Y, Zhu X F, Garcia-Vidal F J, Yin X B, Zhang W L, Zhang X 2013 Sci. Rep. 3 1728
Google Scholar
[42] Jia H, Lu M H, Ni X, Bao M, Li X D 2014 J. Appl. Phys. 116 124504
Google Scholar
[43] Ooi K, Okada T, Tanaka K 2011 Phys. Rev. B 84 115405
Google Scholar
[44] Xie P X, Sheng Z Q, Huang Z X, Hu P, Wu H W 2023 Appl. Phys. Lett. 122 222202
Google Scholar
[45] Morse P, Ingard K 1986 Theoretical Acoustics (Princeton: Princeton University Press
[46] 张孝悦, 徐华锋, 陈婉娜, 周农, 孙文军, 吴宏伟 2024 73 144301
Google Scholar
Zhang X Y, Xu H F, Chen W N, Zhou N, Sun W J, Wu H W 2024 Acta Phys. Sin. 73 144301
Google Scholar
DownLoad:
Metrics
- Abstract views: 418
- PDF Downloads: 7
- Cited By: 0
