Bandgap and transmission spectrum characteristics of multilayered acoustic metamaterials with magnetorheological elastomer

Liu Shao-Gang; Zhao Yue-Chao; Zhao Dan

doi:10.7498/aps.68.20191334

Abstract

One of the challenges relating to acoustic metamaterials is to achieve a tunable performance without modifying the structure. In this paper, we propose two types of acoustic metamaterials with a magnetorheological elastomer (MRE), and their tunable band gap structures and the transmission spectra are investigated by the finite element method (FEM). The MRE acts as a cladding layer, and its shear modulus can be changed by an externally applied magnetic field. The cell resonance frequency of acoustic metamaterial is changed. The band gap structures and the transmission spectra of the two kinds of acoustic metamaterials are calculated under various magnetic fields, and it is found that the frequency and width of band gap, the maximum attenuation frequency and transmission loss of transmission spectrum increase with externally applied magnetic field intensity increasing. Meanwhile, two types of the mass-spring models are used to estimate the band gap frequencies of the two kinds of acoustic metamaterials. The FEM results are in good agreement with the estimation results. In addition, the effects of material parameters of core and shell and filling rate on the band gap and transmission spectrum are also studied. The effects of core material parameters on the band gap and transmission spectrum of single-layer acoustic metamaterial are analyzed. It is found that the core mass has an effect on the band gap frequency and width, and the elastic parameter of the core affects the transmission loss of the transmission spectrum. The influences of core and shell material parameter on the band gap and transmission spectrum of double-layer acoustic metamaterial is analyzed by the control variable method. The results show that the core and shell mass affect the band gap frequency, width and pass-band width, and the elastic parameter of the core and the shell affect the transmission loss of the transmission spectrum. As the filling rate increases, the band gap frequency and width of the single- and double-layer MRE acoustic metamaterial increase, the maximum attenuation frequency of the transmission spectrum does not change, and the transmission loss increases. These results will greatly contribute to the application of acoustic metamaterials to controlling the active noise and vibration.

Keywords:

acoustic metamaterials /
magnetorheological elastomer cladding layers /
bandgap and transmission spectra /
magnetic field intensity

Authors and contacts

College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China

Corresponding author: Zhao Dan, heuzhaodan@outlook.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51675111, 51775123)

FullText HTML : translate this paragraph

References

[1]	Chen M, Xu W S, Liu Y, Yan K, Jiang H, Wang Y R 2018 Appl. Acoust. 139 235 Google Scholar
[2]	Sheng P, Mei J, Liu Z Y, Wen W J 2007 Physica B 394 256 Google Scholar
[3]	Fang N C, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452 Google Scholar
[4]	张永燕, 吴九汇, 钟宏民 2017 66 094301 Google Scholar Zhang Y Y, Wu J H, Zhong H M 2017 Acta Phys. Sin. 66 094301 Google Scholar
[5]	Xia B Z, Chen N, Xie L X, Qin Y, Yu D J 2016 Appl. Acoust. 112 1 Google Scholar
[6]	Yasuda H, Yang J 2015 Phys. Rev. Lett. 114 185502 Google Scholar
[7]	Zhu X F 2013 Phys. Lett. A 377 1784 Google Scholar
[8]	Xiao W, Zeng G W, Cheng Y S 2008 Appl. Acoust. 69 255 Google Scholar
[9]	Romero-García V, Krynkin A, Garcia-Raffi L M, Umnova O, Sánchez-Pérez J V 2013 J. Sound Vibr. 332 184 Google Scholar
[10]	Krushynska A O, Kouznetsova V G, Geers M G D 2014 J. Mech. Phys. Solids 71 179 Google Scholar
[11]	Zhou X L, Xu Y L, Liu Y, Lü L L, Peng F J, Wang L Q 2018 Appl. Acoust. 133 97 Google Scholar
[12]	Wu L Y, Chiang T Y, Tsai C N, Wu M L, Chen L W 2012 Appl. Phys. A 109 523 Google Scholar
[13]	Li D, Zigoneanu L, Popa B, Cummer S A 2012 J. Acoust. Soc. Am. 132 2823 Google Scholar
[14]	Zhu R R, Ma C, Zheng B, Musa M Y, Jing L Q, Yang Y H, Wang H P, Dehdashti S, Fang N X, Chen H S 2017 Appl. Phys. Lett. 110 113503 Google Scholar
[15]	Bi Y F, Jia H, Lu W J, Ji P F, Yang J 2017 Sci. Rep. 7 705 Google Scholar
[16]	沈惠杰, 温激鸿, 郁殿龙, 蔡力, 温熙森 2012 61 134303 Google Scholar Shen H J, Wen J H, Yu D L, Cai L, Wen X S 2012 Acta Phys. Sin. 61 134303 Google Scholar
[17]	Chen H Y, Chan C T 2007 Appl. Phys. Lett. 91 183518 Google Scholar
[18]	Zhu X F, Liang B, Kan W W, Zou X Y, Cheng J C 2011 Phys. Rev. Lett. 106 014301 Google Scholar
[19]	Zhu X F, Ramezani H, Shi C Z, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
[20]	刘松, 罗春荣, 翟世龙, 陈怀军, 赵晓鹏 2017 66 024301 Google Scholar Liu S, Luo C R, Zhai S L, Chen H J, Zhao X P 2017 Acta Phys. Sin. 66 024301 Google Scholar
[21]	Peng Y G, Qin C Z, Zhao D G, Shen Y X, Xu X Y, Bao M, Jia H, Zhu X F 2016 Nat. Commun. 7 13368 Google Scholar
[22]	Zhu Y F, Hu J, Fan X D, Yang J, Liang B, Zhu X F, Cheng J C 2018 Nat. Commun. 9 1632 Google Scholar
[23]	Zhu X F, Li K, Zhang P, Zhu J, Zhang J T, Tian C, Liu S C 2016 Nat. Commun. 7 11731 Google Scholar
[24]	Zhu X F, Liu S C, Xu T, Wang T H, Cheng J C 2010 Chin. Phys. B 19 044301 Google Scholar
[25]	Zhu X F, Xu T, Liu S C, Cheng J C 2009 J. Appl. Phys. 106 104901 Google Scholar
[26]	Zhu X F, Zou X Y, Liang B, Cheng J C 2015 J. Appl. Phys. 108 124909
[27]	Liu Z Y, Zhang X X, Mao Y W, Zhu Y Y, Yang Z Y, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[28]	Li J, Chan C T 2004 Phys. Rev. E 70 055602 Google Scholar
[29]	Goffaux C, Vigneron J P 2001 Phys. Rev. B 64 075118 Google Scholar
[30]	Bertoldi K, Boyce M C 2008 Phys. Rev. B 77 052105
[31]	Larabi H, Pennec Y, Djafari-Rouhani B, Vasseur J O 2007 Phys. Rev. E 75 066601 Google Scholar
[32]	Lewińska M A, Kouznetsova V G, van Dommelen J A W, Krushynska A O, Geers M G D 2017 Int. J. Solids Struct. 126–127 163
[33]	Gao W T, Xia J P, Sun H X, Yuan S Q, Ge Y, Liu X J 2019 Appl. Phys. Express 12 044002 Google Scholar
[34]	Cheng Y, Zhou C, Yuan B G, Wu D J, Wei Q, Liu X J 2015 Nat. Mater. 14 1013 Google Scholar
[35]	Zhu X F, Liang B, Kan W W, Peng Y G, Cheng J C 2016 Phys. Rev. Appl. 5 054015 Google Scholar
[36]	Chen S B, Wang G, Wen J H, Wen X S 2013 J. Sound Vibr. 332 1520 Google Scholar
[37]	Chen S B, Wen J H, Wang G, Wen X S 2013 Chin. Phys. B 22 074301 Google Scholar
[38]	Xiao S W, Ma G C, Li Y, Yang Z Y, Sheng P 2015 Appl. Phys. Lett. 106 091904 Google Scholar
[39]	贺子厚, 赵静波, 姚宏, 蒋娟娜, 陈鑫 2019 68 134302 Google Scholar He Z H, Zhao J B, Yao H, Jiang J N, Chen X 2019 Acta Phys. Sin. 68 134302 Google Scholar
[40]	Shen Y X, Zhu X F, Cai F Y, Ma T, Li F, Xia X X, Li Y C, Wang C Z, Zheng H R 2019 Phys. Rev. Appl. 11 034009 Google Scholar
[41]	Zhou X L, Chen C Q 2013 Physica B 431 23 Google Scholar
[42]	Carlson J D, Jolly M R 2000 Mechatronics 10 555 Google Scholar
[43]	Ginder J M, Clark S M, Schlotter W F, Nichols M E 2002 Int. J. Mod. Phys. B 16 472
[44]	Chen L, Gong X L, Jiang W Q, Yao J J, Xia D H, Li W H 2007 J. Mater. Sci. 42 5483 Google Scholar
[45]	Chen X, Xu X C, Ai S G, Chen H S, Pei Y M 2014 Appl. Phys. Lett. 105 071913 Google Scholar
[46]	Xu Z L, Tong J, Wu F G 2018 Solid State Commun. 271 51 Google Scholar
[47]	Wu B, He C F, Wei R J, Zhao H Y 2009 IEEE International Ultrasonics Symposium Beijing, China, November 2−5, 2008 p1484
[48]	Davis L C 1999 J. Appl. Phys. 85 3348 Google Scholar
[49]	Wang G, Shao L H, Liu Y Z, Wen J H 2006 Chin. Phys. B 15 1843 Google Scholar
[50]	张帅, 郭书祥, 姚宏, 赵静波, 蒋娟娜, 张吉宁, 贺子厚 2018 人工晶体学报 47 1 Google Scholar Zhang S, Guo S X, Yao H, Zhao J B, Jiang J N, Zhang J N, He Z H 2018 J. Synth. Cryst. 47 1 Google Scholar

Cited By

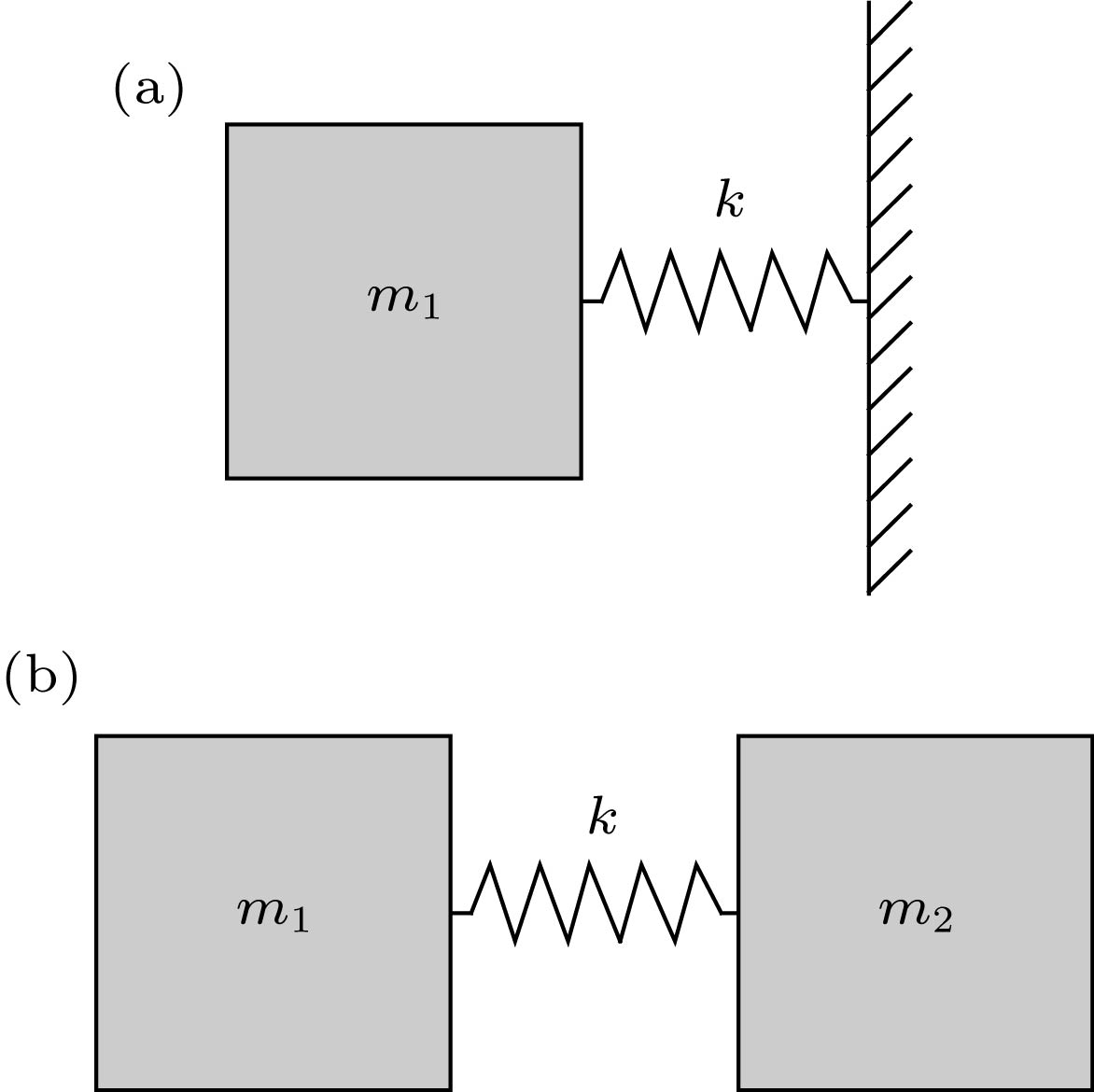
图 1 MRE包覆层声学超材料元胞结构和不可约布里渊区　(a) 单包覆层MRE声学超材料; (b) 双包覆层MRE声学超材料; (c) 正方晶格第一不可约布里渊区

Figure 1. Schematic of the MRE acoustic metamaterial cells and the irreducible first Brillouin zone: (a) Single-layer MRE acoustic metamaterial; (b) double-layer MRE acoustic metamaterial; (c) the irreducible first Brillouin zone of square lattices.

DownLoad: Full-Size Img PowerPoint

图 2 单包覆层MRE声学超材料带隙结构　(a) 磁场强度H = 0; (b) 磁场强度H = 6 kOe

Figure 2. The band gap structures of single-layer MRE acoustic metamaterial: (a) Magnetic field intensity of H = 0; (b) magnetic field intensity of H = 6 kOe.

DownLoad: Full-Size Img PowerPoint

图 3 单包覆层MRE声学超材料带隙边界位移场　(a) 带隙下边界; (b) 带隙上边界

Figure 3. Displacement field of the band gap boundaries of the single-layer MRE acoustic metamaterial: (a) The lower boundary of the band gap; (b) the upper boundary of the band gap.

DownLoad: Full-Size Img PowerPoint

图 4 单包覆层MRE声学超材料的质量-弹簧模型　(a) 带隙下边界; (b) 带隙上边界

Figure 4. The mass-spring model of single-layer MRE acoustic metamaterial: (a) Lower boundary of band gap; (b) upper boundary of band gap.

DownLoad: Full-Size Img PowerPoint

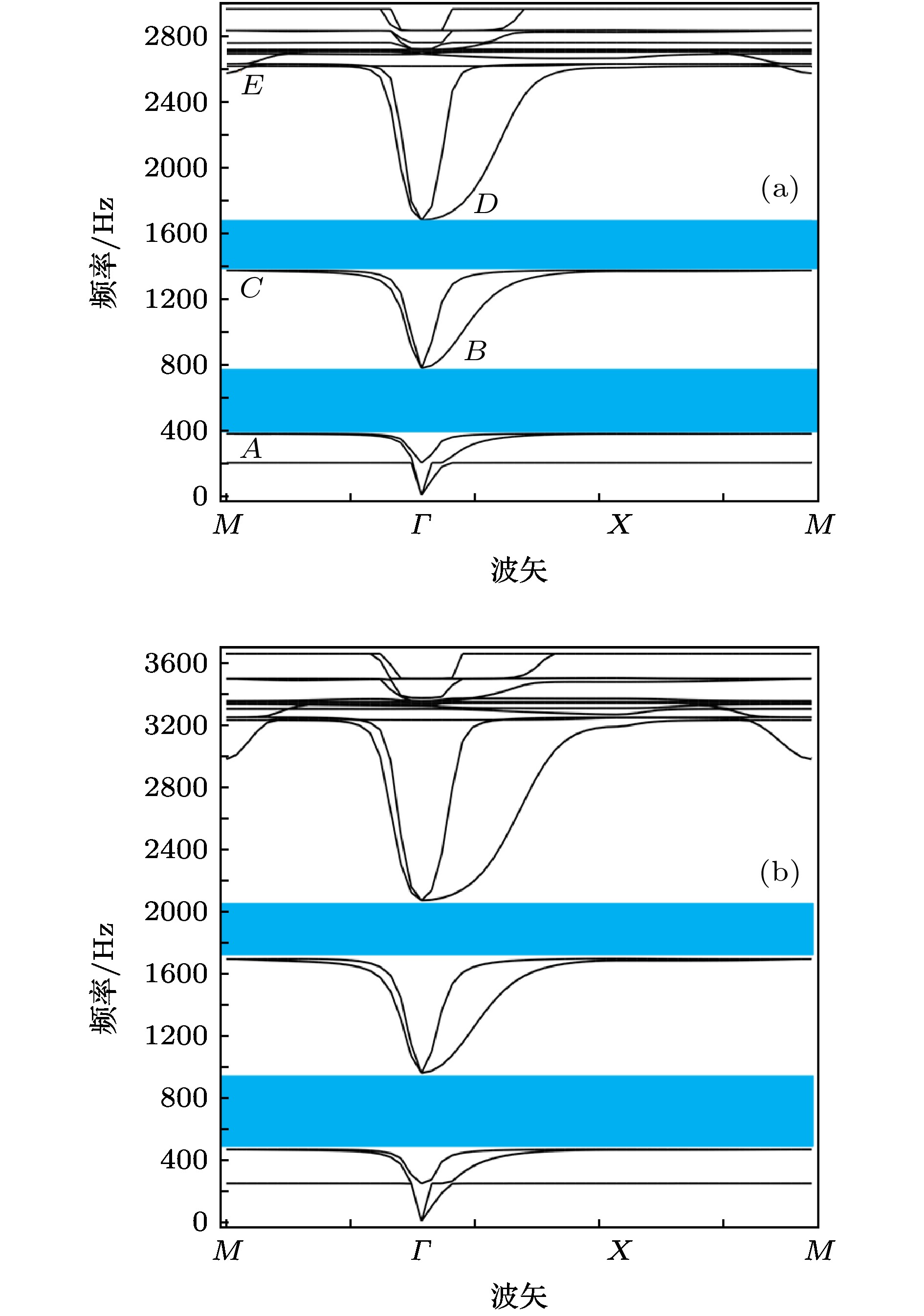
图 5 单包覆层MRE声学超材料带隙随磁场强度变化及有限元法与质量-弹簧模型对比　(a) 磁场强度H = 0—10 kOe; (b) 有限元法与质量弹簧-模型对比

Figure 5. Dependence of the band gap boundaries on the applied magnetic field of single-layer MRE acoustic metamaterial and a comparison of the FEM and the mass-spring model for (a) magnetic field intensity of H = 0–10 kOe, (b) comparison of the FEM and mass-spring model.

DownLoad: Full-Size Img PowerPoint

图 6 单包覆层MRE声学超材料带隙随材料和结构参数变化　(a) 随芯体质量增加变化; (b) 随填充率增加变化

Figure 6. The band gap of single-layer MRE acoustic metamaterial changes with (a) the core mass and (b) the filling rate.

DownLoad: Full-Size Img PowerPoint

图 7 双包覆层MRE声学超材料带隙结构　(a) H = 0; (b) H = 6 kOe

Figure 7. The band gap structures of the double-layer MRE acoustic metamaterial: (a) H = 0; (b) H = 6 kOe.

DownLoad: Full-Size Img PowerPoint

图 8 双包覆层MRE声学超材料带隙边界处位移向量场　(a) 第一阶带隙下边界; (b) 第一阶带隙上边界; (c) 第二阶带隙下边界; (d) 第二阶带隙上边界; (e) 图7(a)中E点

Figure 8. Displacement field of the band gap boundaries of the double-layer MRE acoustic metamaterial: (a) The lower boundary and (b) the upper boundary of the first band gaps; (c) the lower boundary and (d) the upper boundary of the second band gap; (e) point E in Fig.7 (a).

DownLoad: Full-Size Img PowerPoint

图 9 双包覆层MRE声学超材料质量-弹簧模型　(a) 第一阶与第二阶带隙下边界; (b) 第一阶与第二阶带隙上边界

Figure 9. The mass-spring model of the double-layer MRE acoustic metamaterial: (a) Lower boundary of the first and second band gap; (b) upper boundary of the first and second band gap.

DownLoad: Full-Size Img PowerPoint

图 10 双包覆层MRE声学超材料带隙随磁场强度变化及有限元法与质量-弹簧模型对比　(a) 磁场强度H = 0—10 kOe; (b) 有限元法与质量-弹簧模型对比

Figure 10. Dependence of the band gap boundaries on the applied magnetic field of double-layer MRE acoustic metamaterial and a comparison of the FEM and mass-spring model for (a) magnetic field intensity of H = 0–10 kOe, (b) comparison of the FEM and mass-spring model.

DownLoad: Full-Size Img PowerPoint

图 11 双包覆层MRE声学超材料带隙随材料和结构参数变化　(a) 芯体质量增加; (b) 壳体质量增加; (c) 填充率增加

Figure 11. The band gap of double-layer MRE acoustic metamaterial changes with (a) the core mass, (b) the shell mass, (c) the filling rate.

DownLoad: Full-Size Img PowerPoint

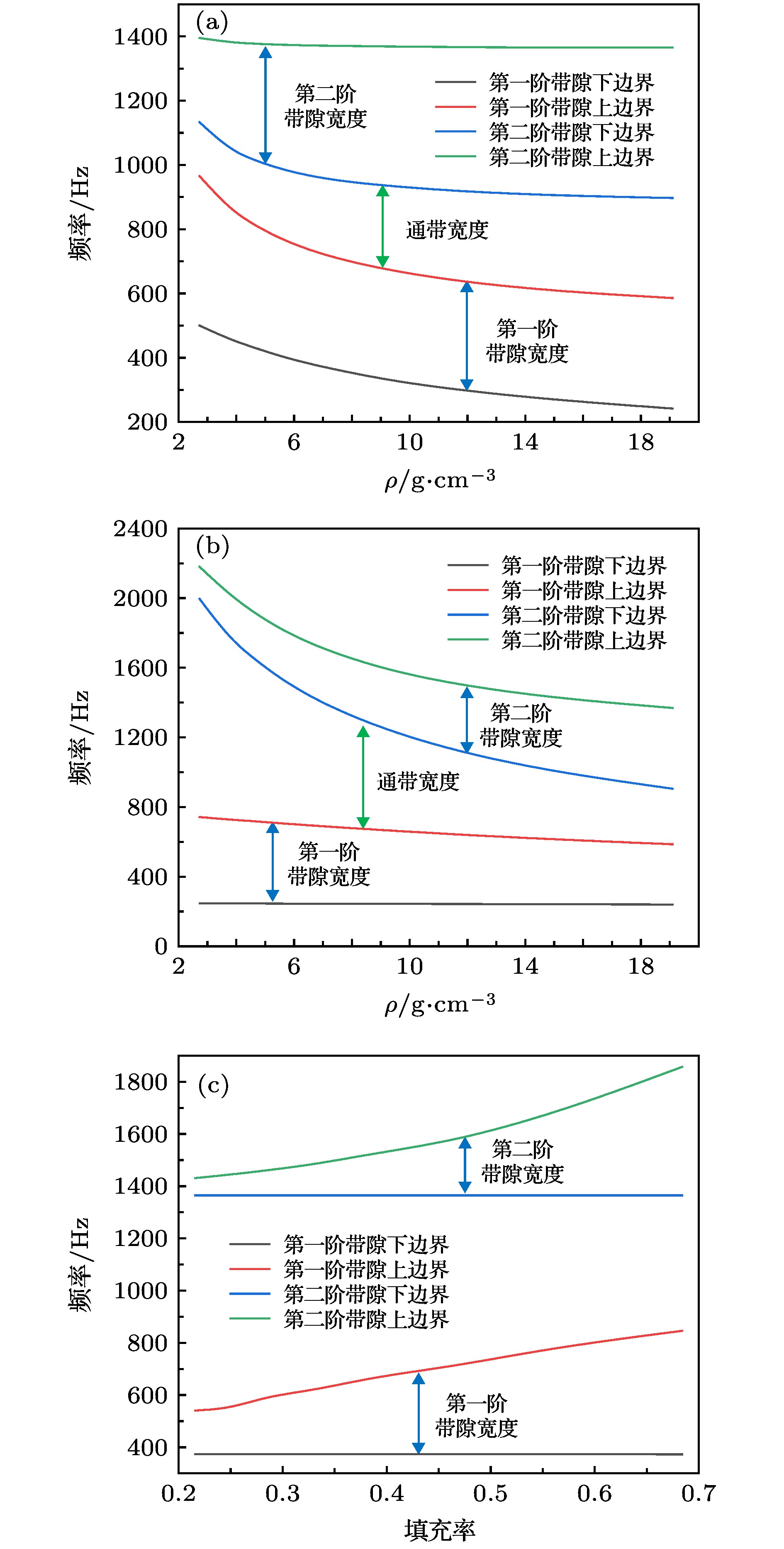
图 12 单包覆层MRE声学超材料传输谱变化　(a) 磁场强度为0, 4, 6, 8 kOe; (b) 芯体材料分别为铝、钛、铜、铅和钨; (c) 填充率增加

Figure 12. Transmission spectra of single-layer MRE acoustic metamaterial change with (a) At magnetic field intensity of 0, 4, 6, and 8 kOe, (b) core materials for aluminum, titanium, copper, lead, and tungsten, (c) the filling rate.

DownLoad: Full-Size Img PowerPoint

图 13 双包覆层MRE声学超材料传输谱变化　(a) 磁场强度为0, 4, 6, 8 kOe; (b) 芯体材料分别为铝、钛、铜、铅和钨; (c) 壳体材料分别为铝、钛、铜、铅和钨; (d) 随填充率变化

Figure 13. Transmission spectra change of double-layer MRE acoustic metamaterial: (a) At the magnetic field intensity of 0, 4, 6, and 8 kOe; (b) with the core materials for aluminum, titanium, copper, lead, and tungsten, (c) with the shell materials of aluminum, titanium, copper, lead, and tungsten, (d) with filling rate.

DownLoad: Full-Size Img PowerPoint

表 1 构成MRE声学超材料的材料参数

Table 1. Material properties of the MRE acoustic metamaterials.

材料密度$\rho /{\rm{kg}} \cdot {{\rm{m}}^{ - 3}}$ 拉梅常数
λ/GPa μ/GPa

纯铁 7900 115.38 76.92
环氧树脂 1180 4.52 1.59
MRE 3009 6.26×10^-3 0.4×10^-3

DownLoad: CSV

表 2 材料参数

Table 2. The material parameters.

材料密度ρ/kg·m^–3 弹性参数
弹性模量E/GPa 泊松比$\upsilon $

钨 19100 344 0.28
铅 11600 16 0.42
铜 8950 115 0.32
钛 4540 102 0.3
铝 2730 68 0.33

DownLoad: CSV

map

[1]	Chen M, Xu W S, Liu Y, Yan K, Jiang H, Wang Y R 2018 Appl. Acoust. 139 235 Google Scholar
[2]	Sheng P, Mei J, Liu Z Y, Wen W J 2007 Physica B 394 256 Google Scholar
[3]	Fang N C, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452 Google Scholar
[4]	张永燕, 吴九汇, 钟宏民 2017 66 094301 Google Scholar Zhang Y Y, Wu J H, Zhong H M 2017 Acta Phys. Sin. 66 094301 Google Scholar
[5]	Xia B Z, Chen N, Xie L X, Qin Y, Yu D J 2016 Appl. Acoust. 112 1 Google Scholar
[6]	Yasuda H, Yang J 2015 Phys. Rev. Lett. 114 185502 Google Scholar
[7]	Zhu X F 2013 Phys. Lett. A 377 1784 Google Scholar
[8]	Xiao W, Zeng G W, Cheng Y S 2008 Appl. Acoust. 69 255 Google Scholar
[9]	Romero-García V, Krynkin A, Garcia-Raffi L M, Umnova O, Sánchez-Pérez J V 2013 J. Sound Vibr. 332 184 Google Scholar
[10]	Krushynska A O, Kouznetsova V G, Geers M G D 2014 J. Mech. Phys. Solids 71 179 Google Scholar
[11]	Zhou X L, Xu Y L, Liu Y, Lü L L, Peng F J, Wang L Q 2018 Appl. Acoust. 133 97 Google Scholar
[12]	Wu L Y, Chiang T Y, Tsai C N, Wu M L, Chen L W 2012 Appl. Phys. A 109 523 Google Scholar
[13]	Li D, Zigoneanu L, Popa B, Cummer S A 2012 J. Acoust. Soc. Am. 132 2823 Google Scholar
[14]	Zhu R R, Ma C, Zheng B, Musa M Y, Jing L Q, Yang Y H, Wang H P, Dehdashti S, Fang N X, Chen H S 2017 Appl. Phys. Lett. 110 113503 Google Scholar
[15]	Bi Y F, Jia H, Lu W J, Ji P F, Yang J 2017 Sci. Rep. 7 705 Google Scholar
[16]	沈惠杰, 温激鸿, 郁殿龙, 蔡力, 温熙森 2012 61 134303 Google Scholar Shen H J, Wen J H, Yu D L, Cai L, Wen X S 2012 Acta Phys. Sin. 61 134303 Google Scholar
[17]	Chen H Y, Chan C T 2007 Appl. Phys. Lett. 91 183518 Google Scholar
[18]	Zhu X F, Liang B, Kan W W, Zou X Y, Cheng J C 2011 Phys. Rev. Lett. 106 014301 Google Scholar
[19]	Zhu X F, Ramezani H, Shi C Z, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
[20]	刘松, 罗春荣, 翟世龙, 陈怀军, 赵晓鹏 2017 66 024301 Google Scholar Liu S, Luo C R, Zhai S L, Chen H J, Zhao X P 2017 Acta Phys. Sin. 66 024301 Google Scholar
[21]	Peng Y G, Qin C Z, Zhao D G, Shen Y X, Xu X Y, Bao M, Jia H, Zhu X F 2016 Nat. Commun. 7 13368 Google Scholar
[22]	Zhu Y F, Hu J, Fan X D, Yang J, Liang B, Zhu X F, Cheng J C 2018 Nat. Commun. 9 1632 Google Scholar
[23]	Zhu X F, Li K, Zhang P, Zhu J, Zhang J T, Tian C, Liu S C 2016 Nat. Commun. 7 11731 Google Scholar
[24]	Zhu X F, Liu S C, Xu T, Wang T H, Cheng J C 2010 Chin. Phys. B 19 044301 Google Scholar
[25]	Zhu X F, Xu T, Liu S C, Cheng J C 2009 J. Appl. Phys. 106 104901 Google Scholar
[26]	Zhu X F, Zou X Y, Liang B, Cheng J C 2015 J. Appl. Phys. 108 124909
[27]	Liu Z Y, Zhang X X, Mao Y W, Zhu Y Y, Yang Z Y, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[28]	Li J, Chan C T 2004 Phys. Rev. E 70 055602 Google Scholar
[29]	Goffaux C, Vigneron J P 2001 Phys. Rev. B 64 075118 Google Scholar
[30]	Bertoldi K, Boyce M C 2008 Phys. Rev. B 77 052105
[31]	Larabi H, Pennec Y, Djafari-Rouhani B, Vasseur J O 2007 Phys. Rev. E 75 066601 Google Scholar
[32]	Lewińska M A, Kouznetsova V G, van Dommelen J A W, Krushynska A O, Geers M G D 2017 Int. J. Solids Struct. 126–127 163
[33]	Gao W T, Xia J P, Sun H X, Yuan S Q, Ge Y, Liu X J 2019 Appl. Phys. Express 12 044002 Google Scholar
[34]	Cheng Y, Zhou C, Yuan B G, Wu D J, Wei Q, Liu X J 2015 Nat. Mater. 14 1013 Google Scholar
[35]	Zhu X F, Liang B, Kan W W, Peng Y G, Cheng J C 2016 Phys. Rev. Appl. 5 054015 Google Scholar
[36]	Chen S B, Wang G, Wen J H, Wen X S 2013 J. Sound Vibr. 332 1520 Google Scholar
[37]	Chen S B, Wen J H, Wang G, Wen X S 2013 Chin. Phys. B 22 074301 Google Scholar
[38]	Xiao S W, Ma G C, Li Y, Yang Z Y, Sheng P 2015 Appl. Phys. Lett. 106 091904 Google Scholar
[39]	贺子厚, 赵静波, 姚宏, 蒋娟娜, 陈鑫 2019 68 134302 Google Scholar He Z H, Zhao J B, Yao H, Jiang J N, Chen X 2019 Acta Phys. Sin. 68 134302 Google Scholar
[40]	Shen Y X, Zhu X F, Cai F Y, Ma T, Li F, Xia X X, Li Y C, Wang C Z, Zheng H R 2019 Phys. Rev. Appl. 11 034009 Google Scholar
[41]	Zhou X L, Chen C Q 2013 Physica B 431 23 Google Scholar
[42]	Carlson J D, Jolly M R 2000 Mechatronics 10 555 Google Scholar
[43]	Ginder J M, Clark S M, Schlotter W F, Nichols M E 2002 Int. J. Mod. Phys. B 16 472
[44]	Chen L, Gong X L, Jiang W Q, Yao J J, Xia D H, Li W H 2007 J. Mater. Sci. 42 5483 Google Scholar
[45]	Chen X, Xu X C, Ai S G, Chen H S, Pei Y M 2014 Appl. Phys. Lett. 105 071913 Google Scholar
[46]	Xu Z L, Tong J, Wu F G 2018 Solid State Commun. 271 51 Google Scholar
[47]	Wu B, He C F, Wei R J, Zhao H Y 2009 IEEE International Ultrasonics Symposium Beijing, China, November 2−5, 2008 p1484
[48]	Davis L C 1999 J. Appl. Phys. 85 3348 Google Scholar
[49]	Wang G, Shao L H, Liu Y Z, Wen J H 2006 Chin. Phys. B 15 1843 Google Scholar
[50]	张帅, 郭书祥, 姚宏, 赵静波, 蒋娟娜, 张吉宁, 贺子厚 2018 人工晶体学报 47 1 Google Scholar Zhang S, Guo S X, Yao H, Zhao J B, Jiang J N, Zhang J N, He Z H 2018 J. Synth. Cryst. 47 1 Google Scholar

[1]	Liu Quan-Xing, He Zhe-Xing, Li Yong-Qiang, Wen Ji-Hong, Xiao Yong. Double-order coupling bandgap design of metamaterial beams and broadband vibration reduction properties. Acta Physica Sinica, 2024, 73(15): 154601. doi: 10.7498/aps.73.20240689
[2]	Wei Wei, Guan Feng, Fang Xin. Integrated vibration absorption and isolation design method for metamaterial beams based on bandgap wave-insulating vibration isolatior. Acta Physica Sinica, 2024, 73(22): 224602. doi: 10.7498/aps.73.20241135
[3]	Ren Hang, Zhao Dan, Dong Li-Qiang, Liu Shao-Gang, Yang Jin-Shui. Fast and accurate characterization of magnetorheological elastomers based on machine learning. Acta Physica Sinica, 2024, 73(16): 165101. doi: 10.7498/aps.73.20240482
[4]	Xu Qiang-Rong, Zhu Yang, Lin Kang, Shen Cheng, Lu Tian-Jian. Low-frequency sound insulation performance of novel membrane acoustic metamaterial with dynamic negative stiffness. Acta Physica Sinica, 2022, 71(21): 214301. doi: 10.7498/aps.71.20221058
[5]	Shen Hui-Jie, Yu Dian-Long, Tang Zhi-Yin, Su Yong-Sheng, Li Yan-Fei, Liu Jiang-Wei. Characteristics of low-frequency noise elimination in a fluid-filled pipe of dark acoustic metamaterial type. Acta Physica Sinica, 2019, 68(14): 144301. doi: 10.7498/aps.68.20190311
[6]	Zhai Shi-Long, Wang Yuan-Bo, Zhao Xiao-Peng. A kind of tunable acoustic metamaterial for low frequency absorption. Acta Physica Sinica, 2019, 68(3): 034301. doi: 10.7498/aps.68.20181908
[7]	Ding Chang-Lin, Dong Yi-Bao, Zhao Xiao-Peng. Research advances in acoustic metamaterials and metasurface. Acta Physica Sinica, 2018, 67(19): 194301. doi: 10.7498/aps.67.20180963
[8]	Shen Dan-Ping, Zhang Xiao-Dong, Sun Yan, Kang Ting-Ting, Dai Ning, Chu Jun-Hao, Yu Guo-Lin. Magnetotransport property of negative band gap HgCdTe bulk material. Acta Physica Sinica, 2017, 66(24): 247301. doi: 10.7498/aps.66.247301
[9]	Zhang Yong-Yan, Wu Jiu-Hui, Zhong Hong-Min. Low-frequency wide-band mechanism of a new type acoustic metamaterial with negative modulus. Acta Physica Sinica, 2017, 66(9): 094301. doi: 10.7498/aps.66.094301
[10]	Liu Song, Luo Chun-Rong, Zhai Shi-Long, Chen Huai-Jun, Zhao Xiao-Peng. Inverse Doppler effect of acoustic metamaterial with negative mass density. Acta Physica Sinica, 2017, 66(2): 024301. doi: 10.7498/aps.66.024301
[11]	Qing Qian-Jun, Zhou Xin, Xie Fang, Chen Li-Qun, Wang Xin-Jun, Tan Shi-Hua, Peng Xiao-Fang. Characteristics of acoustic phonon transport and thermal conductance in multi-terminal graphene junctions. Acta Physica Sinica, 2016, 65(8): 086301. doi: 10.7498/aps.65.086301
[12]	Lu Zhi-Miao, Cai Li, Wen Ji-Hong, Wen Xi-Sen. Research on coordinate transformation design of a cylinderical acoustic cloak with pentamode materials. Acta Physica Sinica, 2016, 65(17): 174301. doi: 10.7498/aps.65.174301
[13]	Liu Jiao, Hou Zhi-Lin, Fu Xiu-Jun. Mechanism for local resonant acoustic metamaterial. Acta Physica Sinica, 2015, 64(15): 154302. doi: 10.7498/aps.64.154302
[14]	Shen Hui-Jie, Wen Ji-Hong, Yu Dian-Long, Cai Li, Wen Xi-Sen. Research on a cylindrical cloak with active acoustic metamaterial layers. Acta Physica Sinica, 2012, 61(13): 134303. doi: 10.7498/aps.61.134303
[15]	Ding Chang-Lin, Zhao Xiao-Peng, Hao Li-Mei, Zhu Wei-Ren. Acoustic metamaterial with split hollow spheres. Acta Physica Sinica, 2011, 60(4): 044301. doi: 10.7498/aps.60.044301
[16]	Bian Lei-Xiang, Wen Yu-Mei, Li Ping. The field dependence of magnetoelastic damping in magnetostrictive material and its application in the magnetic field sensing. Acta Physica Sinica, 2010, 59(2): 883-892. doi: 10.7498/aps.59.883
[17]	Ding Chang-Lin, Zhao Xiao-Peng. Audible sound metamaterial. Acta Physica Sinica, 2009, 58(9): 6351-6355. doi: 10.7498/aps.58.6351
[18]	E Peng, Han Ke, Wu Zhi-Wen, Yu Da-Ren. On the role of magnetic field intensity effects on the discharge characteristics of Hall thrusters. Acta Physica Sinica, 2009, 58(4): 2535-2542. doi: 10.7498/aps.58.2535
[19]	Han Liang, Zhao Yu-Qing, Zhang Hai-Bo. The research on half-analytical method in calculating the magnetic field of unbalanced magnetron sputtering. Acta Physica Sinica, 2008, 57(2): 996-1000. doi: 10.7498/aps.57.996
[20]	LI XIANG-TING, MA HONG-RU. ELECTROSTATIC FIELD IN ELECTRORHEOLOGICAL FLUIDS:A SEMI-ANALYTICAL METHOD. Acta Physica Sinica, 2000, 49(6): 1070-1075. doi: 10.7498/aps.49.1070

Catalog

Vol. 68, Issue 23 - 2019-12-05

Metrics

Abstract views: 9051
PDF Downloads: 129
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板