-
As an important second-generation semiconductor material, indium phosphide (InP) possesses excellent advantages such as a wide bandgap, high electron mobility, high photoelectric conversion efficiency, and strong radiation resistance. It is considered an excellent material for electronic devices in aerospace applications. However, point defects generated by space radiation particles in InP electronic devices can cause their electrical performance to degrade severely. In this study, first-principles calculations are employed to investigate the stable structures of point defects in InP and calculate the migration energy values of nearest-neighbor defects. Four stable structures of In vacancies and three stable structures of P vacancies are identified by constructing the stable structures of point defects in different charge states. The migration process of vacancy defects is studied, revealing that the migration energy of P vacancies is higher than that of In vacancies. Moreover, charged vacancy defects exhibit higher migration energy values than neutral vacancies. Regarding the migration process of interstitial defects, it is found that the migration energy of interstitial defects is smaller than that of vacancy defects. In the calculation of In interstitial migration process with different charge states, two different migration processes are found. Besides, during the migration calculations of P interstitial, a special intermediate state is discovered, resulting in multiple paths migrating to the nearest-neighbor position in the migration energy barrier diagram. The research results are helpful to understand the formation mechanism and migration behavior of defects in InP materials, and are important in designing and manufacturing InP devices with long-term stable operation in space environment.
-
Keywords:
- InP /
- first principles /
- point defects /
- migration
[1] Mokkapati S, Jagadish C 2009 Mater. Today 12 22
Google Scholar
[2] Beling A, Campbell J C 2009 J. Lightwave Technol. 27 343
Google Scholar
[3] 白雨蓉, 李永宏, 刘方, 廖文龙, 何欢, 杨卫涛, 贺朝会 2021 70 172401
Google Scholar
Bai Y R, Li Y H, Liu F, Liao W L, He H, Yang W T, He C H 2021 Acta Phys. Sin. 70 172401
Google Scholar
[4] 李薇, 白雨蓉, 郭昊轩, 贺朝会, 李永宏 2022 71 082401
Google Scholar
Li W, Bai Y R, Guo H X, He C H, Li Y H 2022 Acta Phys. Sin. 71 082401
Google Scholar
[5] Rathi S, Jogi J, Gupta M, Gupta R S 2009 Microelectron. Reliab. 49 1508
Google Scholar
[6] Bauer S, Sichkovskyi V, Schnabel F, Sengül A, Reithmaier J P 2019 J. Cryst. Growth 516 34
Google Scholar
[7] Shamirzaev T S, Debus J, Abramkin D S, Dunker D, Yakovlev D R, Dmitriev D V, Gutakovskii A K, Braginsky L S, Zhuravlev K S, Bayer M 2011 Phys. Rev. B 84 155318
Google Scholar
[8] Mehrer H 2007 Diffusion in Solids (Berlin, Heidelberg: Springer Verlag
[9] Wright A F, Modine N A 2016 J. Appl. Phys. 120 215705
Google Scholar
[10] Wampler W R, Myers S M 2015 J. Appl. Phys. 117 045707
Google Scholar
[11] Myers S M, Cooper P J, Wampler W R 2008 J. Appl. Phys. 104 044507
Google Scholar
[12] 贺朝会, 唐杜, 李永宏, 臧航 2019 原子能科学技术 53 2106
Google Scholar
He C H, Tang D, Li Y H, Zang H 2019 At. Energy Sci. Technol. 53 2106
Google Scholar
[13] 唐杜, 贺朝会, 臧航, 李永宏, 熊涔, 张晋新, 张鹏, 谭鹏康 2016 65 084209
Google Scholar
Tang D, He C H, Zang H, Li Y H, Xiong C, Zhang J X, Zhang P, Tan P K 2016 Acta Phys. Sin. 65 084209
Google Scholar
[14] Ogura M, Mizuta M, Onaka K, Kukimoto H 1983 Jpn. J. Appl. Phys. 22 1502
Google Scholar
[15] Tapster P R 1983 J. Cryst. Growth 64 200
Google Scholar
[16] Rybicki G C, Zorman C A 1994 J. Appl. Phys. 75 3187
Google Scholar
[17] Walters R J, Summers G P 1991 J. Appl. Phys. 69 6488
Google Scholar
[18] Ando K, Yamaguchi M, Uemura C 1986 Phys. Rev. B 34 3041
Google Scholar
[19] McAfee S R, Capasso F, Lang D V, Hutchinson A, Bonner W A 1981 J. Appl. Phys. 52 6158
Google Scholar
[20] Liu J, Song Y, Xu X, Li W, Yang J, Li X 2023 J. Appl. Phys. 134 115702
Google Scholar
[21] Mishra R, Restrepo O D, Kumar A, Windl W 2012 J. Mater. Sci. 47 7482
Google Scholar
[22] Zollo G, Gala F 2012 New J. Phys. 14 053036
Google Scholar
[23] El-Mellouhi F, Mousseau N 2006 Phys. Rev. B 74 205207
Google Scholar
[24] Levasseur-Smith K, Mousseau N 2008 J. Appl. Phys. 103 113502
Google Scholar
[25] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15
Google Scholar
[26] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[27] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[28] Basic Parameters of Indium Phosphide (InP) https://www.ioffe.ru/SVA/NSM/Semicond/InP/basic.html [2024-04-04]
[29] Pluengphon P, Bovornratanaraks T, Pinsook U 2017 J. Alloys Compd. 700 98
Google Scholar
[30] Bastos C M O, Sabino F P, Sipahi G M, Da Silva J L F 2018 J. Appl. Phys. 123 065702
Google Scholar
[31] Martienssen W, Warlimont H 2005 Springer Handbook of Condensed Matter and Materials Data (Berlin, Heidelberg: Springer Press) p647
[32] Malouin M A, El-Mellouhi F, Mousseau N 2007 Phys. Rev. B 76 045211
Google Scholar
[33] Schultz P A, von Lilienfeld O A 2009 Modell. Simul. Mater. Sci. Eng. 17 0840007
Google Scholar
-
图 1 InP中不同本征点缺陷稳定结构(红色为In原子, 灰色为P原子, 深蓝色为In/P间隙原子) (a) VIn; (b) VP; (c) Ini; (d) Pi
Figure 1. Stable structures of different intrinsic point defects in InP (red balls denote In atoms, gray balls denote P atoms, and dark blue balls denote In/P interstitial atoms): (a) VIn; (b) VP; (c) Ini; (d) Pi.
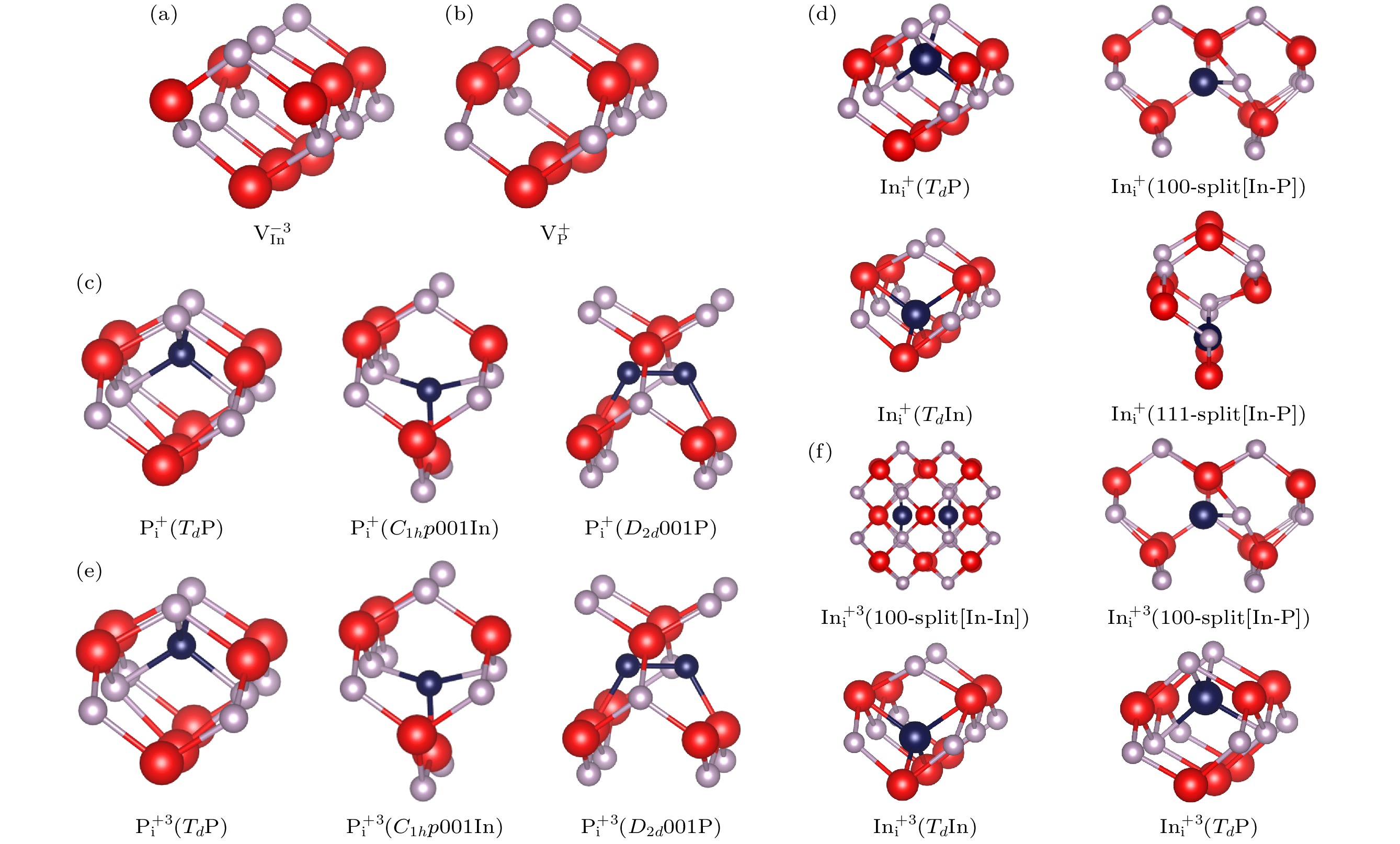
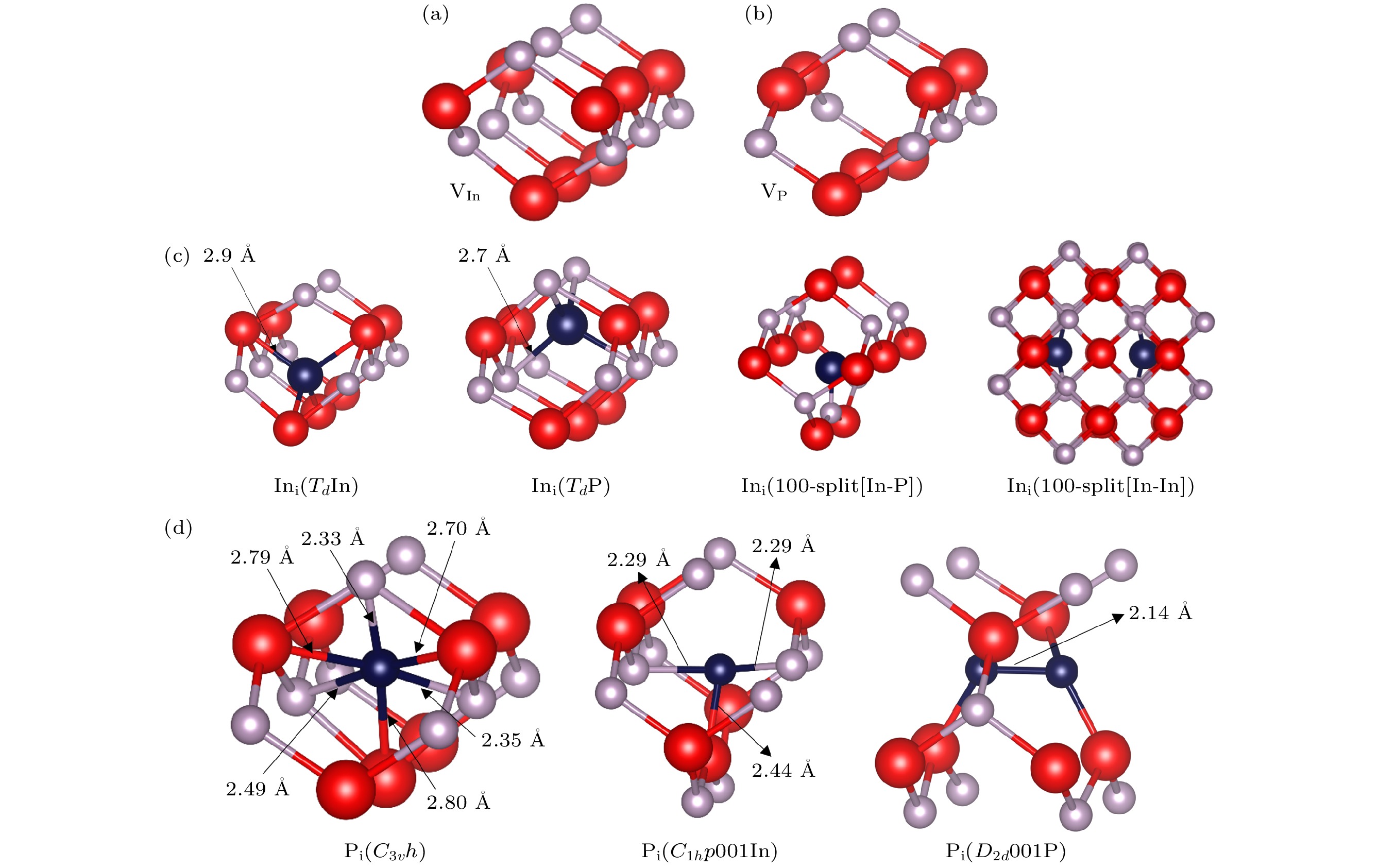
图 2 InP不同带电点缺陷稳定结构(红色为In原子, 灰色为P原子, 深蓝色为In/P间隙原子) (a) ${\text{V}}_{{\text{In}}}^{ - {3}}$; (b) ${\text{V}}_{\text{P}}^ + $; (c) $ {\text{P}}^{+}_{\text{i}} $; (d) $ {\text{In}}_{\text{i}}^{+} $; (e) $ {\text{P}}_{\text{i}}^{{\text{+3}}} $; (f) $ {\text{In}}_{\text{i}}^{{\text{+3}}} $
Figure 2. Stable structures of different charged point defects in InP (red balls denote In atoms, gray balls denote P atoms, and dark blue balls denote In/P interstitial atoms): (a) ${\text{V}}_{{\text{In}}}^{ - {3}}$; (b) ${\text{V}}_{\text{P}}^ + $; (c) $ {\text{P}}^{+}_{\text{i}} $; (d) $ {\text{In}}_{\text{i}}^{+} $; (e) $ {\text{P}}_{\text{i}}^{{\text{+3}}} $; (f) $ {\text{In}}_{\text{i}}^{{\text{+3}}} $.
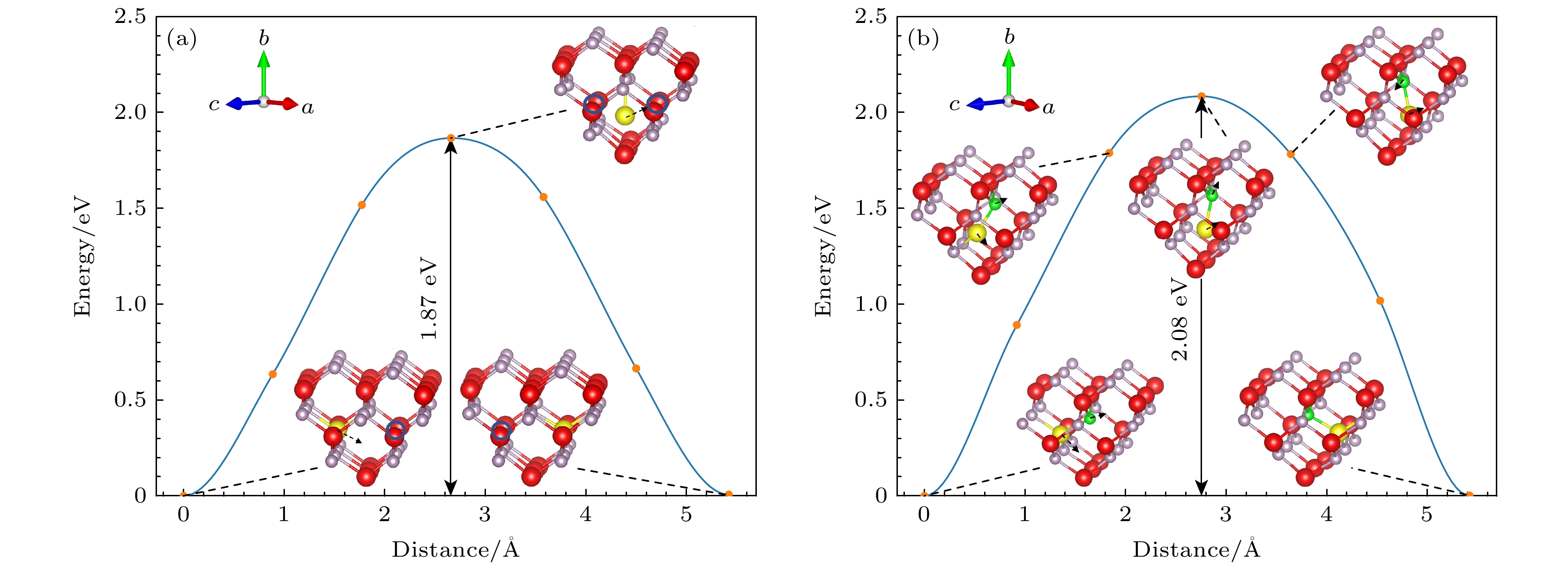
图 3 InP中不同In空位点缺陷迁移能垒图(红色为In原子, 灰色为P原子, 黄色为迁移的In原子, 绿色为迁移的P原子) (a) VIn; (b) ${\text{V}}_{{\text{In}}}^{ - {3}}$
Figure 3. Migration energy barrier diagram for different In vacancy defects in InP (red balls denote In atoms, gray balls denote P atoms, the yellow ball denote the migrating In atom and the green ball is the migrating P atom): (a) VIn; (b) ${\text{V}}_{{\text{In}}}^{ - {3}}$.
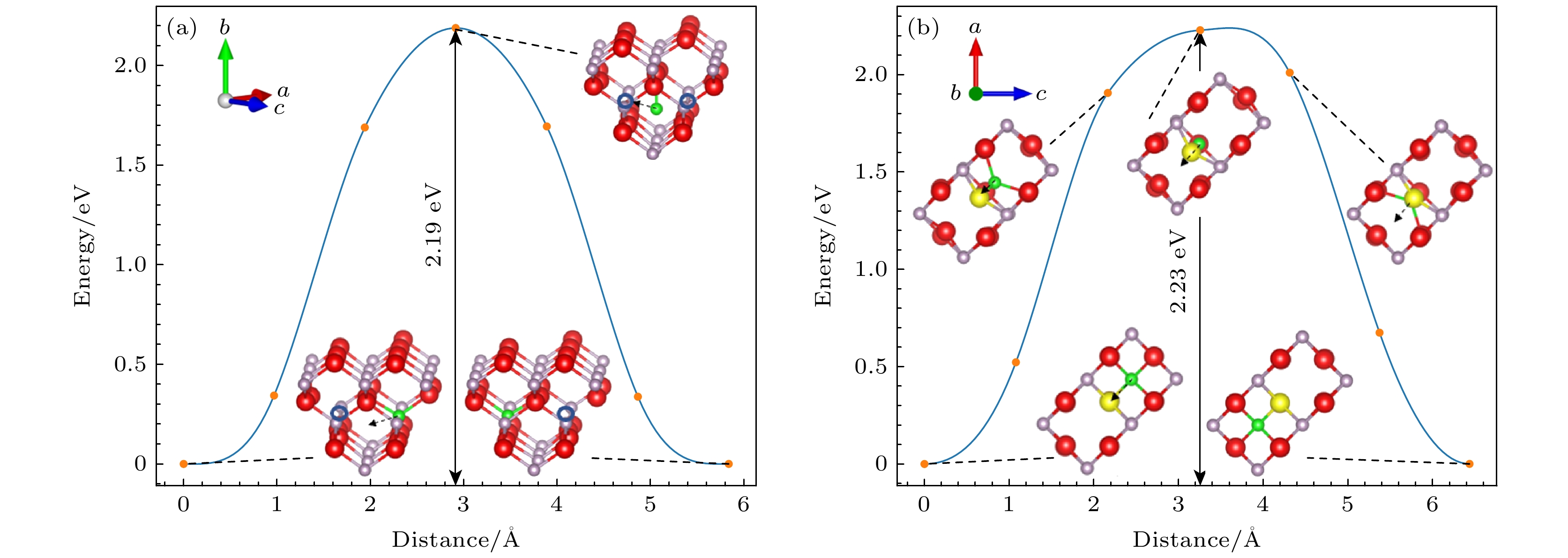
图 4 InP中不同P空位点缺陷迁移能垒图(红色为In原子, 灰色为P原子, 黄色为迁移的In原子, 绿色为迁移的P原子) (a) VP; (b) ${\text{V}}_{\text{P}}^ + $
Figure 4. Migration energy barrier diagram for different P vacancy defects in InP (red balls denote In atoms, gray balls denote P atoms and the green ball is the migrating P atom): (a) VP; (b) ${\text{V}}_{\text{P}}^ + $.
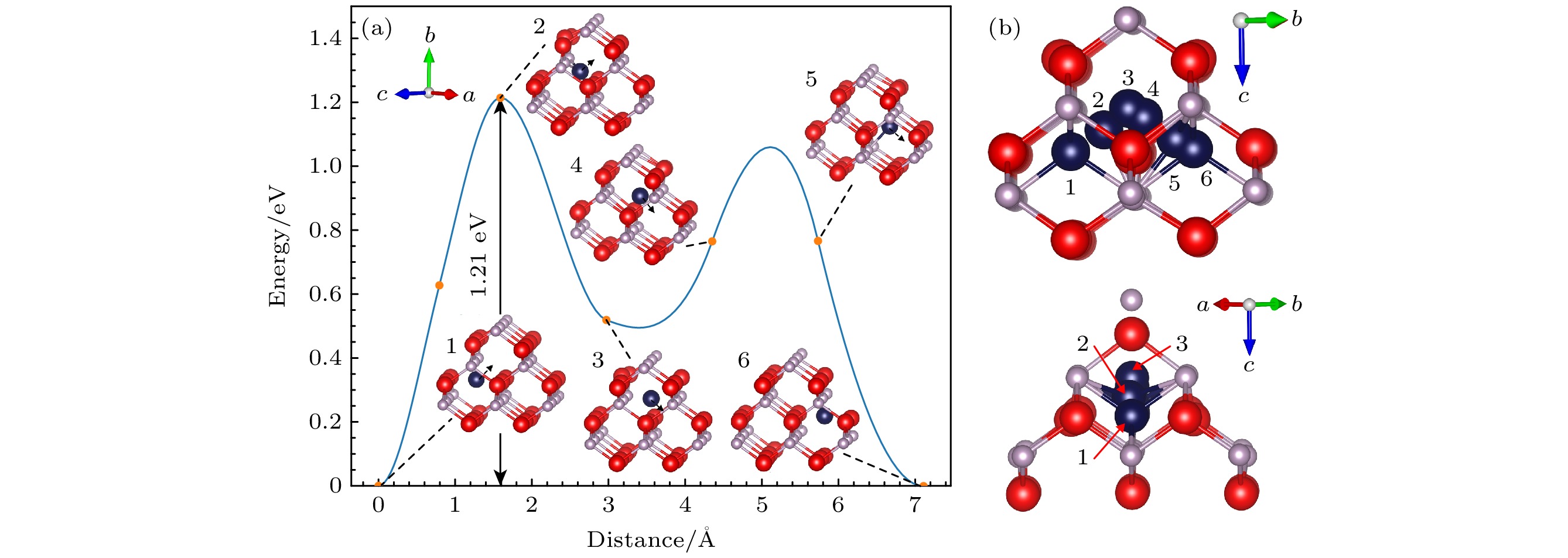
图 5 InP中${\rm In}^{+3}_{\rm i} $迁移能垒图(红色为In原子, 灰色为P原子, 深蓝色为In间隙原子) (a) 迁移能垒图; (b) 能垒图各结构相对位置
Figure 5. ${\rm In}^{+3}_{\rm i} $ point defect migration energy barrier diagram in InP (red balls denote In atoms, gray balls denote P atoms, and dark blue balls denote In interstitial atoms): (a) Migration energy barrier diagram; (b) relative positions of structures in energy barrier diagram.
图 6 InP中$ {\text{In}}_{\text{i}}^{+} $迁移能垒图(红色为In原子, 灰色为P原子, 深蓝色为In间隙原子) (a) 迁移能垒图; (b) 能垒图各结构相对位置
Figure 6. $ {\text{In}}_{\text{i}}^{+} $ point defect migration energy barrier diagram in InP (red balls denote In atoms, gray balls denote P atoms, and dark blue balls denote In interstitial atoms): (a) Migration energy barrier diagram; (b) relative positions of structures in energy barrier diagram.
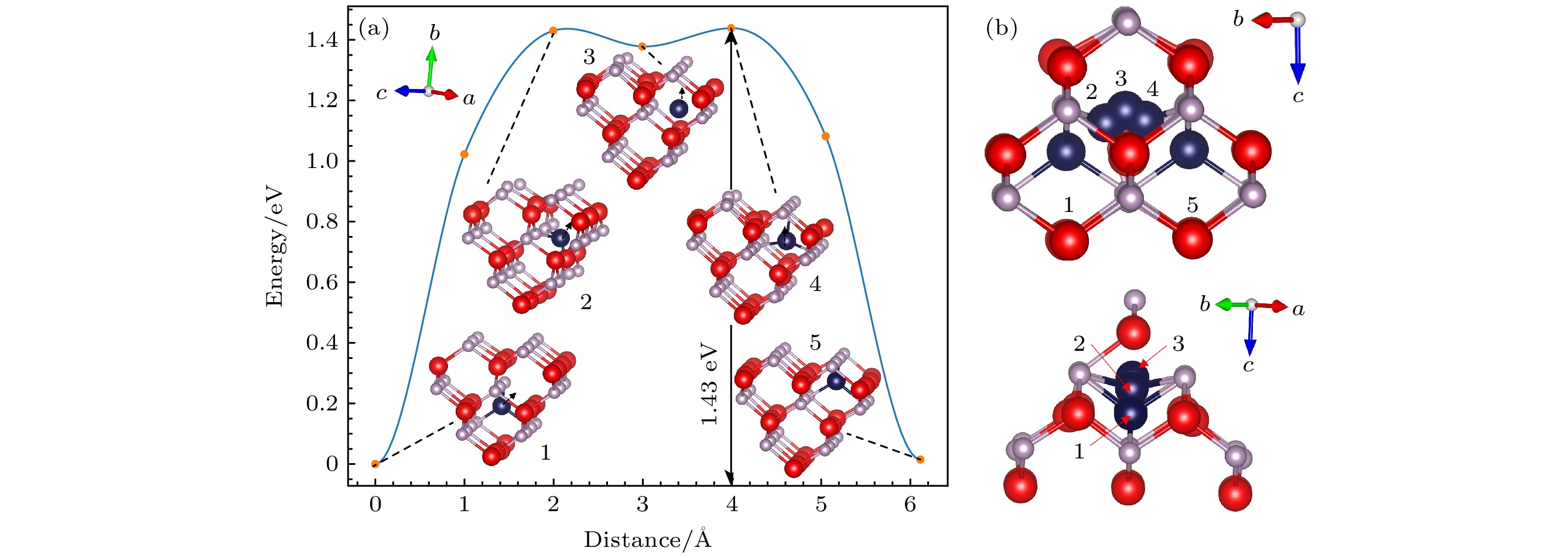
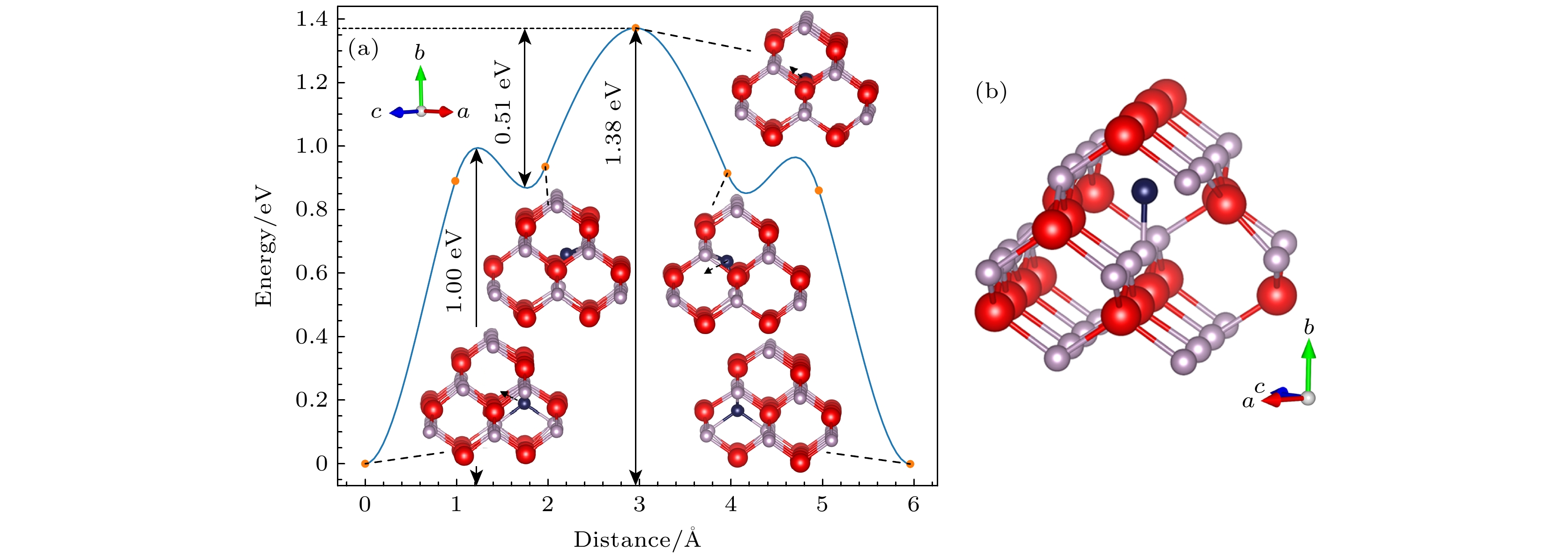
图 7 InP中$ {\text{P}}_{\text{i}}^{{\text{+3}}} $迁移能垒图(红色为In原子, 灰色为P原子, 深蓝色为P间隙原子) (a) 迁移能垒图; (b) 迁移路径峰值对应结构
Figure 7. Migration energy barrier diagram for $ {\text{P}}_{\text{i}}^{{\text{+3}}} $ point defect in InP (red balls denote In atoms, gray balls denote P atoms, and dark blue balls denote P interstitial atoms): (a) Migration energy barrier diagram; (b) peak corresponding structures.
表 1 不同方法计算的InP弹性性质的理论与实验值对比
Table 1. Comparison of theoretical and experimental values of InP’s elastic properties calculated by different methods.
DownLoad: CSV
表 2 不同本征点缺陷稳定结构体系能量和缺陷形成能汇总表
Table 2. Summary table of energy and formation energy for different intrinsic point defect stable structural systems.
DownLoad: CSV
-
[1] Mokkapati S, Jagadish C 2009 Mater. Today 12 22
Google Scholar
[2] Beling A, Campbell J C 2009 J. Lightwave Technol. 27 343
Google Scholar
[3] 白雨蓉, 李永宏, 刘方, 廖文龙, 何欢, 杨卫涛, 贺朝会 2021 70 172401
Google Scholar
Bai Y R, Li Y H, Liu F, Liao W L, He H, Yang W T, He C H 2021 Acta Phys. Sin. 70 172401
Google Scholar
[4] 李薇, 白雨蓉, 郭昊轩, 贺朝会, 李永宏 2022 71 082401
Google Scholar
Li W, Bai Y R, Guo H X, He C H, Li Y H 2022 Acta Phys. Sin. 71 082401
Google Scholar
[5] Rathi S, Jogi J, Gupta M, Gupta R S 2009 Microelectron. Reliab. 49 1508
Google Scholar
[6] Bauer S, Sichkovskyi V, Schnabel F, Sengül A, Reithmaier J P 2019 J. Cryst. Growth 516 34
Google Scholar
[7] Shamirzaev T S, Debus J, Abramkin D S, Dunker D, Yakovlev D R, Dmitriev D V, Gutakovskii A K, Braginsky L S, Zhuravlev K S, Bayer M 2011 Phys. Rev. B 84 155318
Google Scholar
[8] Mehrer H 2007 Diffusion in Solids (Berlin, Heidelberg: Springer Verlag
[9] Wright A F, Modine N A 2016 J. Appl. Phys. 120 215705
Google Scholar
[10] Wampler W R, Myers S M 2015 J. Appl. Phys. 117 045707
Google Scholar
[11] Myers S M, Cooper P J, Wampler W R 2008 J. Appl. Phys. 104 044507
Google Scholar
[12] 贺朝会, 唐杜, 李永宏, 臧航 2019 原子能科学技术 53 2106
Google Scholar
He C H, Tang D, Li Y H, Zang H 2019 At. Energy Sci. Technol. 53 2106
Google Scholar
[13] 唐杜, 贺朝会, 臧航, 李永宏, 熊涔, 张晋新, 张鹏, 谭鹏康 2016 65 084209
Google Scholar
Tang D, He C H, Zang H, Li Y H, Xiong C, Zhang J X, Zhang P, Tan P K 2016 Acta Phys. Sin. 65 084209
Google Scholar
[14] Ogura M, Mizuta M, Onaka K, Kukimoto H 1983 Jpn. J. Appl. Phys. 22 1502
Google Scholar
[15] Tapster P R 1983 J. Cryst. Growth 64 200
Google Scholar
[16] Rybicki G C, Zorman C A 1994 J. Appl. Phys. 75 3187
Google Scholar
[17] Walters R J, Summers G P 1991 J. Appl. Phys. 69 6488
Google Scholar
[18] Ando K, Yamaguchi M, Uemura C 1986 Phys. Rev. B 34 3041
Google Scholar
[19] McAfee S R, Capasso F, Lang D V, Hutchinson A, Bonner W A 1981 J. Appl. Phys. 52 6158
Google Scholar
[20] Liu J, Song Y, Xu X, Li W, Yang J, Li X 2023 J. Appl. Phys. 134 115702
Google Scholar
[21] Mishra R, Restrepo O D, Kumar A, Windl W 2012 J. Mater. Sci. 47 7482
Google Scholar
[22] Zollo G, Gala F 2012 New J. Phys. 14 053036
Google Scholar
[23] El-Mellouhi F, Mousseau N 2006 Phys. Rev. B 74 205207
Google Scholar
[24] Levasseur-Smith K, Mousseau N 2008 J. Appl. Phys. 103 113502
Google Scholar
[25] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15
Google Scholar
[26] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[27] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[28] Basic Parameters of Indium Phosphide (InP) https://www.ioffe.ru/SVA/NSM/Semicond/InP/basic.html [2024-04-04]
[29] Pluengphon P, Bovornratanaraks T, Pinsook U 2017 J. Alloys Compd. 700 98
Google Scholar
[30] Bastos C M O, Sabino F P, Sipahi G M, Da Silva J L F 2018 J. Appl. Phys. 123 065702
Google Scholar
[31] Martienssen W, Warlimont H 2005 Springer Handbook of Condensed Matter and Materials Data (Berlin, Heidelberg: Springer Press) p647
[32] Malouin M A, El-Mellouhi F, Mousseau N 2007 Phys. Rev. B 76 045211
Google Scholar
[33] Schultz P A, von Lilienfeld O A 2009 Modell. Simul. Mater. Sci. Eng. 17 0840007
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1086
- PDF Downloads: 44
- Cited By: 0
