Wavelength-selective thermal emission metasurfaces based on synthetic dimensional topological Weyl points

Lai Zhen-Xin; Zhang Ye; Zhong Fan; Wang Qiang; Xiao Yan-Ling; Zhu Shi-Ning; Liu Hui

doi:10.7498/aps.73.20240512

Abstract

Blackbody emission such as the emission from incandescent sources usually possesses a broadband emission spectrum covering the whole infrared wavelength range. Most of emission energy goes into the unwanted infrared range and consequently causes low emission efficiency. Recently, metasurfaces with two-dimensional subwavelength artificial nanostructures have been widely studied due to their flexibility in modulating optical properties, thus providing an ideal platform for controlling thermal emission. The use of synthetic dimension methods in metasurfaces has opened up new avenues for fine-tuning thermal emission, especially highlighting the physical properties beyond traditional three-dimensional systems and rich topological physics. Although it is theoretically possible to explore physical phenomena through complete three-dimensional structures, such structures are difficult to construct in practice. In contrast, studying one-dimensional system or two-dimensional system is more feasible and efficient. The synthetic dimension approach introduces the possibility of manipulating intrinsic degrees of freedom in photon systems by introducing structural or physical parameters. In this work, we propose utilizing synthetic dimension methods to achieve wavelength-selective thermal emission. Firstly, we construct synthetic Weyl point in a superlattice model and validate it theoretically. Subsequently, experimental characterization of synthetic Weyl cones is conducted by using angle-resolved thermal emission spectroscopy (ARTES). The experimental results demonstrate that we can achieve reasonable wavelength-selective thermal emission while suppressing emission at other wavelengths as much as possible. This is essential for practical infrared applications such as thermalphotovoltaics and thermal management devices.

Keywords:

Authors and contacts

1.
Collaborative Innovation Center of Advanced Microstructures, State Key Laboratory of Solid State Microstructures, School of Physics, Nanjing University, Nanjing 210093, China
2.
School of Physics, Southeast University, Nanjing 211189, China

Corresponding author: Liu Hui, liuhui@nju.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12334015, 92163216, 92150302, 62288101, 12004072).

FullText HTML : translate this paragraph

References

[1]	Chu Q Q, Zhong F, Shang X H, Zhang Y, Zhu S N, Liu H 2024 Nanophotonics 13 1279 Google Scholar
[2]	Li A B, Singh S, Sievenpiper D 2018 Nanophotonics 7 989 Google Scholar
[3]	Chen H T, Taylor A J, Yu N F 2016 Rep. Prog. Phys. 79 076401 Google Scholar
[4]	Diem M, Koschny T, Soukoulis C M 2009 Phys. Rev. B 79 033101 Google Scholar
[5]	Doiron C F, Naik G V 2019 Adv. Mater. 31 1904154 Google Scholar
[6]	Zhang X, Liu H, Zhang Z G, Wang Q, Zhu S N 2017 Sci. Rep. 7 41858 Google Scholar
[7]	Zhang X, Zhang Z G, Wang Q, Zhu S N, Liu H 2019 ACS Photonics 6 2671 Google Scholar
[8]	Chu Q Q, Zhang F Y, Zhang Y, Qiao T, Zhu S N, Liu H 2022 Nanophotonics 11 4263 Google Scholar
[9]	Chu Q Q, Zhang F Y, Zhang Y, Zhu S N, Liu H 2023 Opt. Express 31 39832 Google Scholar
[10]	Zhong F, Zhang Y, Zhu S N, Liu H 2021 Opt. Express 29 35216 Google Scholar
[11]	Makhsiyan M, Bouchon P, Jaeck J, Pelouard J L, Haïder R 2015 Appl. Phys. Lett. 107 251103 Google Scholar
[12]	Li J Y, Yu B W, Shen S 2020 Phys. Rev. Lett. 124 137401 Google Scholar
[13]	Kudyshev Z A, Kildishev A V, Shalaev V M, Boltasseva A 2020 Appl. Phys. Rev. 7 021407 Google Scholar
[14]	Streyer W, Feng K, Zhong Y, Hoffman A J, Wasserman D 2015 Appl. Phys. Lett. 107 081105 Google Scholar
[15]	Argyropoulos C, Le K Q, Mattiucci N, D'Aguanno G, Alù A 2013 Phys. Rev. B 87 205112 Google Scholar
[16]	Kong A, Cai B Y, Shi P, Yuan X C 2019 Opt. Express 27 30102 Google Scholar
[17]	Liu G Q, Liu X S, Chen J, Li Y Y, Shi L L, Fu G L, Liu Z Q 2019 Sol. Energy Mater. Sol. Cells 190 20 Google Scholar
[18]	Chen C, Liu Y H, Jiang Z Y, Shen C, Zhang Y, Zhong F, Chen L S, Zhu S N, Liu H 2022 Opt. Express 30 13391 Google Scholar
[19]	Xu C L, Qu S B, Pang Y Q, Wang J F, Yan M B, Zhang J Q, Wang Z L, Wang W J 2018 Infrared Phys. Technol. 88 133 Google Scholar
[20]	Zhou J R, Zhan Z G, Zhu F D, Han Y G 2023 ACS Appl. Mater. Interfaces 15 21629 Google Scholar
[21]	Zhu Y, Hou G Z, Wang Q Y, Zhu T, Sun T, Xu J, Chen K J 2022 Nanoscale 14 10816 Google Scholar
[22]	Zou C J, Ren G H, Hossain M M, et al. 2017 Adv. Opt. Mater. 5 1700460 Google Scholar
[23]	Yuan L Q, Lin Q, Xiao M, Fan S H 2018 Optica 5 1396 Google Scholar
[24]	Liu H, Yan Z W, Xiao M, Zhu S N 2021 Acta Opt. Sin. 41 0123002 Google Scholar
[25]	Zhang S C, Hu J P 2001 Science 294 823 Google Scholar
[26]	Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 81 159901 Google Scholar
[27]	Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 Google Scholar
[28]	Tang G J, He X T, Shi F L, Liu J W, Chen X D, Dong J W 2022 Laser Photon. Rev. 16 2100300 Google Scholar
[29]	Kraus Y E, Zilberberg O 2012 Phys. Rev. Lett. 109 116404 Google Scholar
[30]	Mei F, Zhu S L, Zhang Z M, Oh C H, Goldman N 2012 Phys. Rev. A 85 013638 Google Scholar
[31]	Tsomokos D I, Ashhab S, Nori F 2010 Phys. Rev. A 82 052311 Google Scholar
[32]	Yuan L Q, Fan S H 2016 Optica 3 1014 Google Scholar
[33]	Cheng D L, Lustig E, Wang K, Fan S H 2023 Light-Sci. Appl. 12 158 Google Scholar
[34]	Englebert N, Goldman N, Erkintalo M, Mostaan N, Gorza S P, Leo F, Fatome J 2023 Nat. Phys. 19 1014 Google Scholar
[35]	Wang B, Chen T, Zhang X D 2019 Annual Conference of Chinese-Society-of-Optical-Engineering(CSOE)-Quantum Information Technology (AOPC) Beijing, China, July 07–09, 2019
[36]	Cardano F, D'Errico A, Dauphin A, Maffei M, Piccirillo B, de Lisio C, De Filippis G, Cataudella V, Santamato E, Marrucci L, Lewenstein M, Massignan P 2017 Nat. Commun. 8 15516 Google Scholar
[37]	Yang M, Zhang H Q, Liu Z H, Zhou Z W, Zhou X X, Xu J S, Han Y J, Li C F, Guo G C 2023 Sci. Adv. 9 eabp8943 Google Scholar
[38]	Bell B A, Wang K, Solntsev A S, Neshev D N, Sukhorukov A A, Eggleton B J 2017 Optica 4 1433 Google Scholar
[39]	Zhang F X, Feng Y M, Chen X F, Ge L, Wan W J 2020 Phys. Rev. Lett. 124 053901 Google Scholar
[40]	Liu J J, Li Z W, Chen Z G, Tang W Y, Chen A, Liang B, Ma G C, Cheng J C 2022 Phys. Rev. Lett. 129 084301 Google Scholar
[41]	Wang Q, Xiao M, Liu H, Zhu S N, Chan C T 2017 Phys. Rev. X 7 031032
[42]	Yan Z W, Wang Q, Xiao M, Zhao Y L, Zhu S N, Liu H 2021 Phys. Rev. Lett. 127 013901 Google Scholar
[43]	Song W E, Wu S J, Chen C, Chen Y X, Huang C Y, Yuan L Q, Zhu S N, Li T 2023 Phys. Rev. Lett. 130 043803 Google Scholar
[44]	Fan X Y, Xia T Z, Qiu H H, Zhang Q C, Qiu C Y 2022 Phys. Rev. Lett. 128 216403 Google Scholar
[45]	Deng W M, Chen Z M, Li M Y, Guo C H, Tian Z T, Sun K X, Chen X D, Chen W J, Dong J W 2022 Light-Sci. Appl. 11 134 Google Scholar
[46]	Xia S, Lei S, Song D, Lauro L D, Alamgir I, Tang L, Xu J, Morandotti R, Buljan H, Chen Z J A P 2024 Adv. Photon. 6 026005 Google Scholar
[47]	Yang B, Guo Q H, Tremain B, Liu R J, Barr L E, Yan Q H, Gao W L, Liu H C, Xiang Y J, Chen J, Fang C, Hibbins A, Lu L, Zhang S 2018 Science 359 1013 Google Scholar
[48]	Wang Q, Ding K, Liu H, Zhu S N, Chan C T 2020 Opt. Express 28 1758 Google Scholar
[49]	Zhong F, Ding K, Zhang Y, Zhu S N, Chan C T, Liu H 2020 Phys. Rev. Appl. 13 014071 Google Scholar

Cited By

图 1 (a)超晶格的结构示意图; (b)参数为(p, q) = (0, 0)的实验样品对应的SEM扫描图; (c)不同参数下的超晶格色散, 红色虚线标出了超晶格的第一布里渊区边界, 蓝色实线和青色虚线代表参数设置为(p, q)=(0, 0)时的色散曲线, 青色虚线是由于人工加倍原胞周期而产生的能带折叠现象, 黑色虚线是参数(p, q) = (0, 0.2)对应的色散; (d)合成空间中的外尔锥, 紫色虚线是参数空间中对应$ {p}^{2}+{q}^{2}=0.{2}^{2} $的回路, 紫红色圆点是已表征的实验数据点

Figure 1. (a) Schematic structure of the superlattice; (b) SEM picture corresponding to the experimental sample with the parameter (p, q) = (0, 0); (c) dispersion of the superlattice with different parameters, the red dashed line marks the boundary of the first Brillouin zone of the superlattice, the blue solid line and cyan dashed line represent the dispersion curves when the parameter is set to (p, q) = (0, 0), and the folding of the bands resulting from the artificial doubling of the unitcell period is marked by the cyan dashed line, and the black dashed line is the dispersion corresponding to the parameter (p, q) = (0, 0.2); (d) Weyl cones in the synthetic space, the purple dashed line is the loop in the parameter space corresponding to $ {p}^{2}+{q}^{2}=0.{2}^{2} $, and the fuchsia dots are the experimental data points that have been characterized.

DownLoad: Full-Size Img PowerPoint

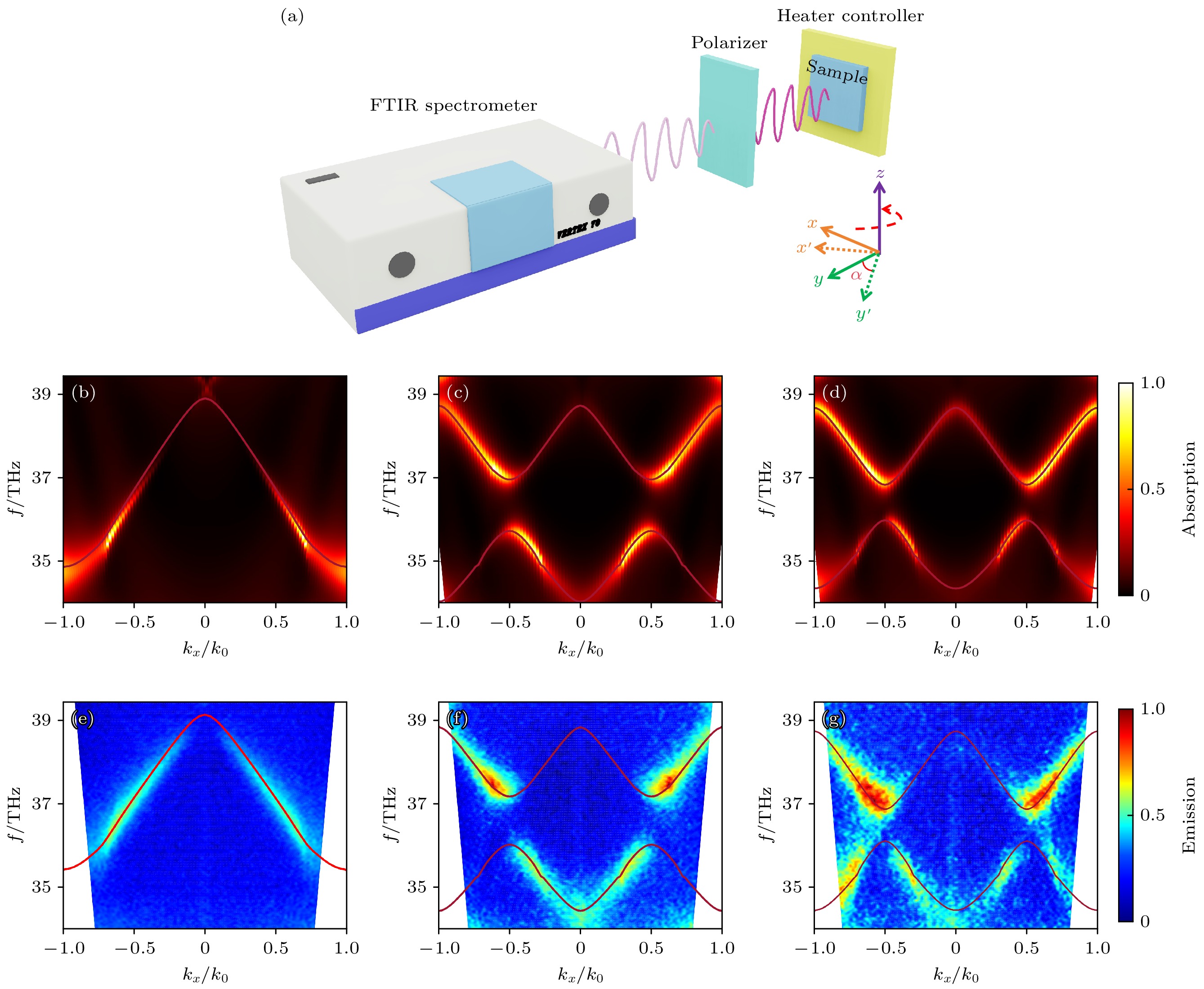
图 2 (a) ARTES测量装置及测量光路图; 由FDTD solutions计算的超晶格吸收谱(b)—(d)以及由ARTES测量的样品热辐射谱(e)—(g); (b), (e) 合成参数$ \left(p, q\right)=\left(0, 0\right) $; (c), (f)合成参数$ \theta =\pi /6 $; (d), (g) 合成参数$ \theta =\pi /3 $, 图片右边的颜色棒代表归一化吸收/辐射强度, 图中的暗红色实线来自COMSOL的仿真结果

Figure 2. (a) ARTES measurement device and measurement optical path diagrams. The superlattice absorption spectra (b)–(d) calculated by FDTD and the thermal emission spectra (e)–(g) of the sample measured by ARTES: (b), (e) Correspond to the synthesis parameter (p, q) = (0, 0); (c), (f) correspond to the synthesis parameter θ = π/6; (d), (g) correspond to the synthesis parameter θ = π/3; colorbar on the right side of the picture represents the normalized absorbed/radiated intensity, and the dark red solid line in the diagram is from the COMSOL multiphysics simulation results.

DownLoad: Full-Size Img PowerPoint

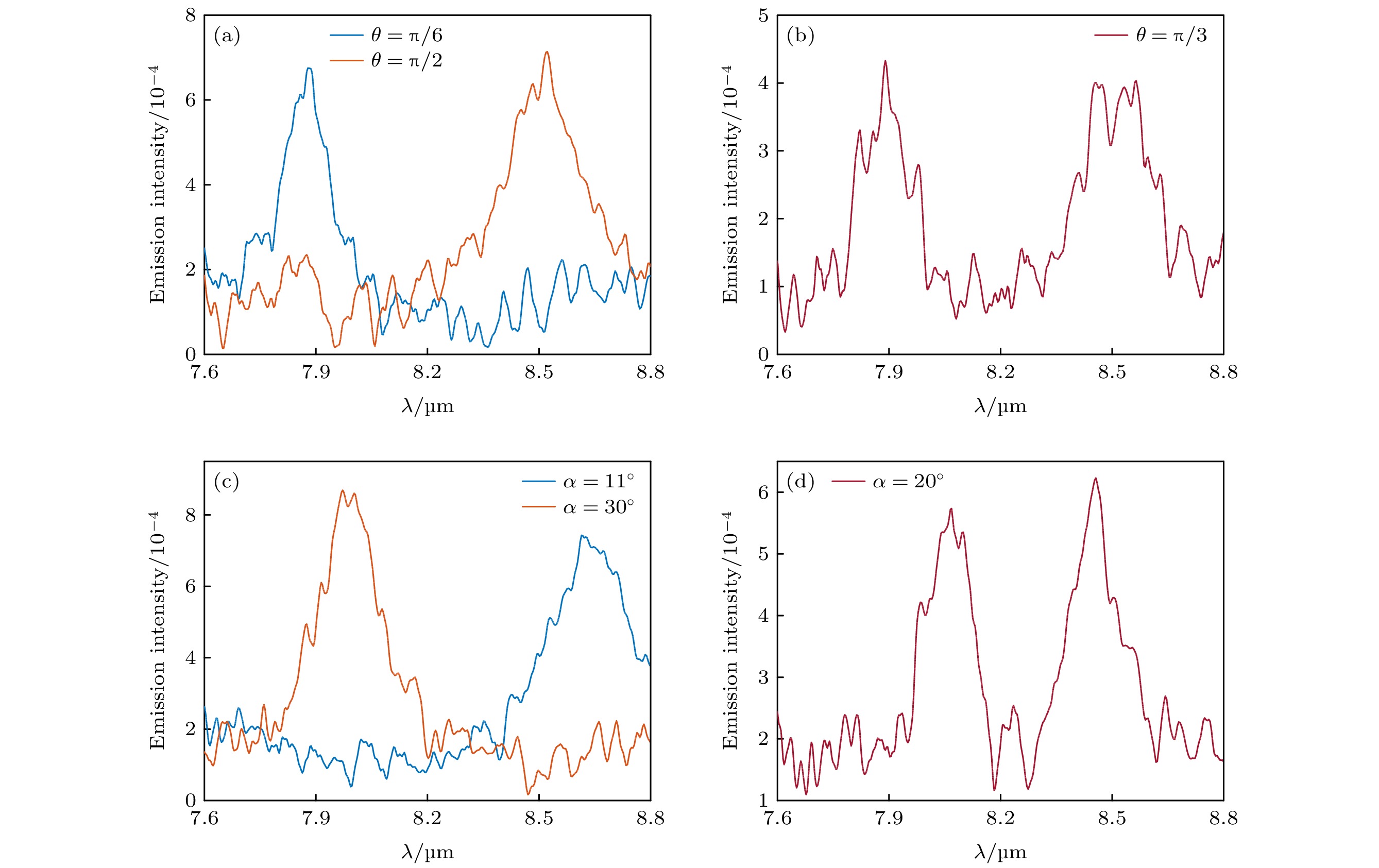
图 3 不同参数下的热辐射谱　(a)热辐射角$ \alpha =35^\circ $时, 不同$ \theta $角对应的热辐射谱; (b) 热辐射角$ \alpha =35^\circ $时, $ \theta ={\mathrm{\pi }}/3 $对应的热辐射谱; (c)热辐射角$ \theta ={\mathrm{\pi }}/6 $时, 不同$ \alpha $角对应的热辐射谱; (d) 热辐射角$ \theta ={\mathrm{\pi }}/6 $时, $ \alpha =20^\circ $对应的热辐射谱

Figure 3. Thermal emission spectra with different parameters: (a) Thermal emission spectrum for different θ at thermal emission angle α = 35°; (b) thermal emission spectrum corresponding to θ = π/3 at thermal emission angle α = 35°; (c) thermal emission spectrum corresponding to θ = π/6 at different thermal emission angle α; (d) thermal emission spectrum corresponding to α = 20° for thermal emission angle θ = π/6

DownLoad: Full-Size Img PowerPoint

图 B1 合成角度θ = π/6, 当波矢为 (a) k_x= 0.2k₀, (b) k_x= 0.4k₀时高频率本征模式的模场分布以及当波矢为(c) k_x= 0.2k₀, (d) k_x= 0.4k₀时低频率本征模式的模场分布; (e) 合成角度θ = π/6时高频率色散对应的TE模式的远场辐射强度; (f) 合成角度θ = π/6时低频率色散对应的TE模式的远场辐射强度

Figure B1. Mode-field distributions of the high-frequency eigenmodes at synthetic angle θ = π/6 when the wave vectors are (a) k_x= 0.2k₀, (b) k_x= 0.4k₀ and the low-frequency eigenmodes when the wave vectors are (c) k_x= 0.2k₀, (d) k_x= 0.4k₀; (e) the far-field radiation intensity of the TE modes corresponding to the high-frequency dispersion at synthetic angle θ = π/6; (f) the far-field radiation intensity of the TE mode corresponding to the low-frequency dispersion at synthetic angle θ = π/6.

DownLoad: Full-Size Img PowerPoint

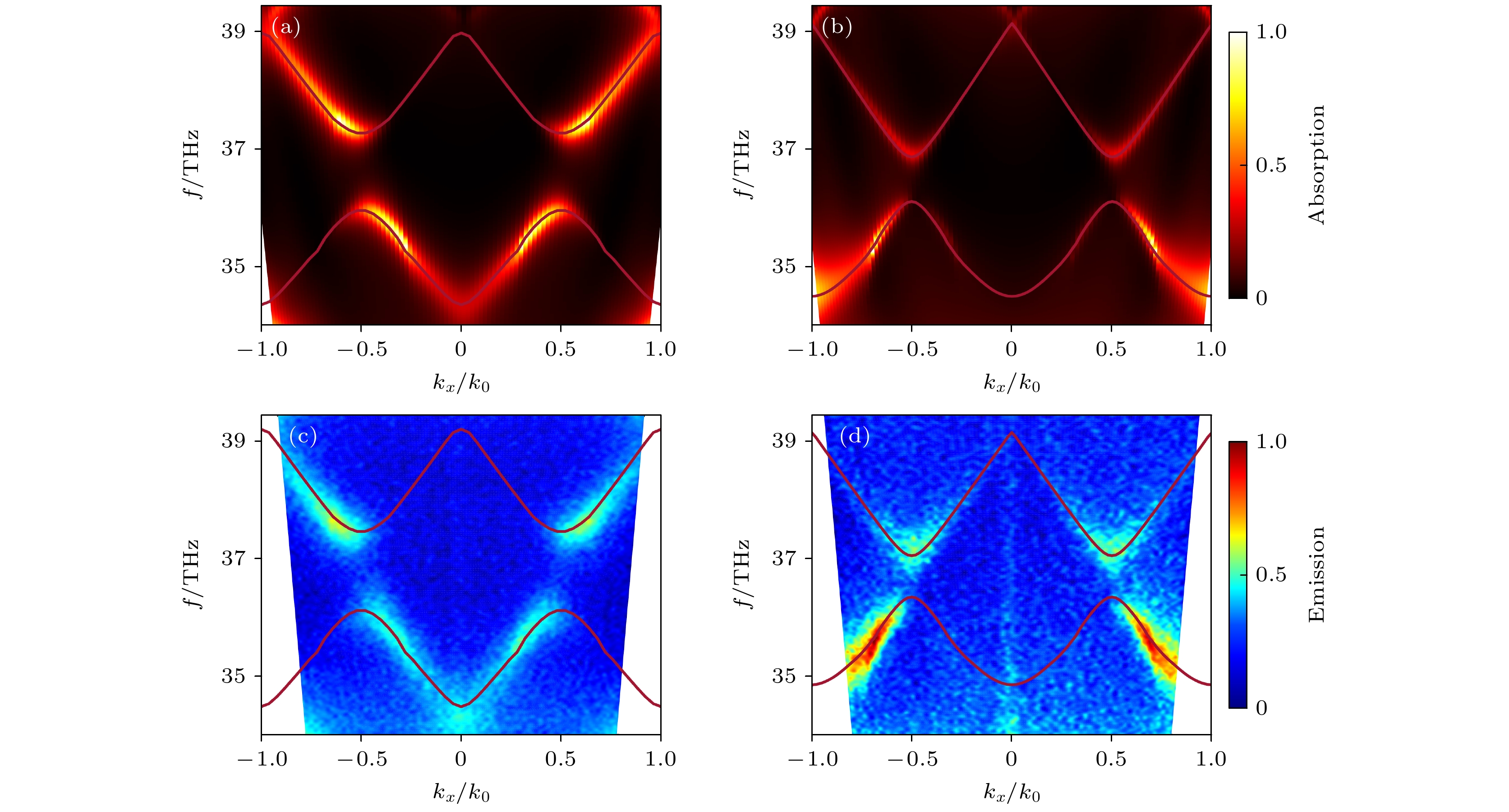
图 A1 由FDTD计算的超晶格吸收谱(a), (b)以及由ARTES测量的样品热辐射谱(c), (d); (a), (c) 合成参数$ \theta =0 $; (b), (d) 合成参数$ \theta ={\mathrm{\pi }}/2 $; 图片右边的颜色棒代表归一化吸收/辐射强度, 图中的暗红色实线来自COMSOL的仿真结果

Figure A1. Superlattice absorption spectra (a), (b) calculated by FDTD and thermal emission spectra (c), (d) of the sample measured by ARTES: (a), (c) Synthesis parameter θ = 0; (b), (d) synthesis parameter θ = π/2; colorbar on the right side of the picture represents normalized absorption/emission intensity, and the dark-red solid line in the picture is from COMSOL simulation result.

DownLoad: Full-Size Img PowerPoint

map

[1]	Chu Q Q, Zhong F, Shang X H, Zhang Y, Zhu S N, Liu H 2024 Nanophotonics 13 1279 Google Scholar
[2]	Li A B, Singh S, Sievenpiper D 2018 Nanophotonics 7 989 Google Scholar
[3]	Chen H T, Taylor A J, Yu N F 2016 Rep. Prog. Phys. 79 076401 Google Scholar
[4]	Diem M, Koschny T, Soukoulis C M 2009 Phys. Rev. B 79 033101 Google Scholar
[5]	Doiron C F, Naik G V 2019 Adv. Mater. 31 1904154 Google Scholar
[6]	Zhang X, Liu H, Zhang Z G, Wang Q, Zhu S N 2017 Sci. Rep. 7 41858 Google Scholar
[7]	Zhang X, Zhang Z G, Wang Q, Zhu S N, Liu H 2019 ACS Photonics 6 2671 Google Scholar
[8]	Chu Q Q, Zhang F Y, Zhang Y, Qiao T, Zhu S N, Liu H 2022 Nanophotonics 11 4263 Google Scholar
[9]	Chu Q Q, Zhang F Y, Zhang Y, Zhu S N, Liu H 2023 Opt. Express 31 39832 Google Scholar
[10]	Zhong F, Zhang Y, Zhu S N, Liu H 2021 Opt. Express 29 35216 Google Scholar
[11]	Makhsiyan M, Bouchon P, Jaeck J, Pelouard J L, Haïder R 2015 Appl. Phys. Lett. 107 251103 Google Scholar
[12]	Li J Y, Yu B W, Shen S 2020 Phys. Rev. Lett. 124 137401 Google Scholar
[13]	Kudyshev Z A, Kildishev A V, Shalaev V M, Boltasseva A 2020 Appl. Phys. Rev. 7 021407 Google Scholar
[14]	Streyer W, Feng K, Zhong Y, Hoffman A J, Wasserman D 2015 Appl. Phys. Lett. 107 081105 Google Scholar
[15]	Argyropoulos C, Le K Q, Mattiucci N, D'Aguanno G, Alù A 2013 Phys. Rev. B 87 205112 Google Scholar
[16]	Kong A, Cai B Y, Shi P, Yuan X C 2019 Opt. Express 27 30102 Google Scholar
[17]	Liu G Q, Liu X S, Chen J, Li Y Y, Shi L L, Fu G L, Liu Z Q 2019 Sol. Energy Mater. Sol. Cells 190 20 Google Scholar
[18]	Chen C, Liu Y H, Jiang Z Y, Shen C, Zhang Y, Zhong F, Chen L S, Zhu S N, Liu H 2022 Opt. Express 30 13391 Google Scholar
[19]	Xu C L, Qu S B, Pang Y Q, Wang J F, Yan M B, Zhang J Q, Wang Z L, Wang W J 2018 Infrared Phys. Technol. 88 133 Google Scholar
[20]	Zhou J R, Zhan Z G, Zhu F D, Han Y G 2023 ACS Appl. Mater. Interfaces 15 21629 Google Scholar
[21]	Zhu Y, Hou G Z, Wang Q Y, Zhu T, Sun T, Xu J, Chen K J 2022 Nanoscale 14 10816 Google Scholar
[22]	Zou C J, Ren G H, Hossain M M, et al. 2017 Adv. Opt. Mater. 5 1700460 Google Scholar
[23]	Yuan L Q, Lin Q, Xiao M, Fan S H 2018 Optica 5 1396 Google Scholar
[24]	Liu H, Yan Z W, Xiao M, Zhu S N 2021 Acta Opt. Sin. 41 0123002 Google Scholar
[25]	Zhang S C, Hu J P 2001 Science 294 823 Google Scholar
[26]	Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 81 159901 Google Scholar
[27]	Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 Google Scholar
[28]	Tang G J, He X T, Shi F L, Liu J W, Chen X D, Dong J W 2022 Laser Photon. Rev. 16 2100300 Google Scholar
[29]	Kraus Y E, Zilberberg O 2012 Phys. Rev. Lett. 109 116404 Google Scholar
[30]	Mei F, Zhu S L, Zhang Z M, Oh C H, Goldman N 2012 Phys. Rev. A 85 013638 Google Scholar
[31]	Tsomokos D I, Ashhab S, Nori F 2010 Phys. Rev. A 82 052311 Google Scholar
[32]	Yuan L Q, Fan S H 2016 Optica 3 1014 Google Scholar
[33]	Cheng D L, Lustig E, Wang K, Fan S H 2023 Light-Sci. Appl. 12 158 Google Scholar
[34]	Englebert N, Goldman N, Erkintalo M, Mostaan N, Gorza S P, Leo F, Fatome J 2023 Nat. Phys. 19 1014 Google Scholar
[35]	Wang B, Chen T, Zhang X D 2019 Annual Conference of Chinese-Society-of-Optical-Engineering(CSOE)-Quantum Information Technology (AOPC) Beijing, China, July 07–09, 2019
[36]	Cardano F, D'Errico A, Dauphin A, Maffei M, Piccirillo B, de Lisio C, De Filippis G, Cataudella V, Santamato E, Marrucci L, Lewenstein M, Massignan P 2017 Nat. Commun. 8 15516 Google Scholar
[37]	Yang M, Zhang H Q, Liu Z H, Zhou Z W, Zhou X X, Xu J S, Han Y J, Li C F, Guo G C 2023 Sci. Adv. 9 eabp8943 Google Scholar
[38]	Bell B A, Wang K, Solntsev A S, Neshev D N, Sukhorukov A A, Eggleton B J 2017 Optica 4 1433 Google Scholar
[39]	Zhang F X, Feng Y M, Chen X F, Ge L, Wan W J 2020 Phys. Rev. Lett. 124 053901 Google Scholar
[40]	Liu J J, Li Z W, Chen Z G, Tang W Y, Chen A, Liang B, Ma G C, Cheng J C 2022 Phys. Rev. Lett. 129 084301 Google Scholar
[41]	Wang Q, Xiao M, Liu H, Zhu S N, Chan C T 2017 Phys. Rev. X 7 031032
[42]	Yan Z W, Wang Q, Xiao M, Zhao Y L, Zhu S N, Liu H 2021 Phys. Rev. Lett. 127 013901 Google Scholar
[43]	Song W E, Wu S J, Chen C, Chen Y X, Huang C Y, Yuan L Q, Zhu S N, Li T 2023 Phys. Rev. Lett. 130 043803 Google Scholar
[44]	Fan X Y, Xia T Z, Qiu H H, Zhang Q C, Qiu C Y 2022 Phys. Rev. Lett. 128 216403 Google Scholar
[45]	Deng W M, Chen Z M, Li M Y, Guo C H, Tian Z T, Sun K X, Chen X D, Chen W J, Dong J W 2022 Light-Sci. Appl. 11 134 Google Scholar
[46]	Xia S, Lei S, Song D, Lauro L D, Alamgir I, Tang L, Xu J, Morandotti R, Buljan H, Chen Z J A P 2024 Adv. Photon. 6 026005 Google Scholar
[47]	Yang B, Guo Q H, Tremain B, Liu R J, Barr L E, Yan Q H, Gao W L, Liu H C, Xiang Y J, Chen J, Fang C, Hibbins A, Lu L, Zhang S 2018 Science 359 1013 Google Scholar
[48]	Wang Q, Ding K, Liu H, Zhu S N, Chan C T 2020 Opt. Express 28 1758 Google Scholar
[49]	Zhong F, Ding K, Zhang Y, Zhu S N, Chan C T, Liu H 2020 Phys. Rev. Appl. 13 014071 Google Scholar

[1]	Cao Wen-Yu, Zhang Ya-Ting, Wei Yan-Feng, Zhu Li-Juan, Xu Ke, Yan Jia-Sheng, Zhou Shu-Xing, Hu Xiao-Dong. Strain modulation effect of superlattice interlayer on InGaN/GaN multiple quantum well. Acta Physica Sinica, 2024, 73(7): 077201. doi: 10.7498/aps.73.20231677
[2]	Wang Ji-Guang, Li Long-Ling, Qiu Jia-Tu, Chen Xu-Min, Cao Dong-Xing. Tuning two-dimensional electron gas at LaAlO₃/KNbO₃ interface by strain gradient. Acta Physica Sinica, 2023, 72(17): 176801. doi: 10.7498/aps.72.20230573
[3]	Fang Xiao-Nan, Wei Qin, Sui Na-Na, Kong Zhi-Yong, Liu Jing, Du Yan-Ling. Spacer-layer-tunable ferromagnetic half-metal-ferromagnetic insulator transition in SrVO₃/SrTiO₃ superlattice. Acta Physica Sinica, 2022, 71(23): 237301. doi: 10.7498/aps.71.20221765
[4]	Wei Hao-Ming, Zhang Ying, Zhang Zhou, Wu Yang-Qing, Cao Bing-Qiang. Influence of polarity compensation on exchange bias field in LaMnO₃/LaNiO₃ superlattices. Acta Physica Sinica, 2022, 71(15): 156801. doi: 10.7498/aps.71.20220365
[5]	Liu Ying-Guang, Ren Guo-Liang, Hao Jiang-Shuai, Zhang Jing-Wen, Xue Xin-Qiang. Thermal conductivity of Si/Ge superlattices containing tilted interface. Acta Physica Sinica, 2021, 70(11): 113101. doi: 10.7498/aps.70.20201807
[6]	Liu Ying-Guang, Hao Jiang-Shuai, Ren Guo-Liang, Zhang Jing-Wen. Thermal conductivities of different period Si/Ge superlattices. Acta Physica Sinica, 2021, 70(7): 073101. doi: 10.7498/aps.70.20201789
[7]	Liu Yan-Fei, Chen Cheng, Yang Dong-Dong, Li Xiu-Jian. Generation of 8 Gb/s physical random numbers based on spontaneous chaotic oscillation of GaAs/Al_0.45Ga_0.55As superlattices. Acta Physica Sinica, 2020, 69(10): 100504. doi: 10.7498/aps.69.20200136
[8]	Li Ting, Lu Xiao-Tong, Zhang Qiang, Kong De-Huan, Wang Ye-Bing, Chang Hong. Evaluation of blackbody-radiation frequency shift in strontium optical lattice clock. Acta Physica Sinica, 2019, 68(9): 093701. doi: 10.7498/aps.68.20182294
[9]	Li Zhu-Song, Steven Zhu. Continuum modeling of thermal transport in superlattices and layered materials for new energy matierlas. Acta Physica Sinica, 2016, 65(11): 116802. doi: 10.7498/aps.65.116802
[10]	Li Yong-Feng, Zhang Jie-Qiu, Qu Shao-Bo, Wang Jia-Fu, Wu Xiang, Xu Zhuo, Zhang An-Xue. Circularly polarized wave reflection focusing metasurfaces. Acta Physica Sinica, 2015, 64(12): 124102. doi: 10.7498/aps.64.124102
[11]	Wang Chang, Cao Jun-Cheng. Nonlinear electron transport in superlattice driven by a terahertz field and a tilted magnetic field. Acta Physica Sinica, 2015, 64(9): 090502. doi: 10.7498/aps.64.090502
[12]	Luo Xiao-Hua. General solution of Schrödinger equation and electron transition in superlattice multi-quantum well. Acta Physica Sinica, 2014, 63(1): 017302. doi: 10.7498/aps.63.017302
[13]	Luo Xiao-Hua, He Wei, Wu Mu-Ying, Luo Shi-Yu. Quasi-periodic excitation and dynamic stability for strained superlattice. Acta Physica Sinica, 2013, 62(24): 247301. doi: 10.7498/aps.62.247301
[14]	Feng Xian-Yang, Lu Yao, Jiang Lei, Zhang Guo-Lian, Zhang Chang-Wen, Wang Pei-Ji. Study of the optical properties of superlattices ZnO doped with indium. Acta Physica Sinica, 2012, 61(5): 057101. doi: 10.7498/aps.61.057101
[15]	Shang Jie, Zhang Hui, Cao Ming-Gang, Zhang Peng-Xiang. Influence of oxygen pressure on the lattice constants of Ba0.6Sr0.4TiO3 thin films and preparation of BaTiO3/Ba0.6Sr0.4TiO3 superlattices. Acta Physica Sinica, 2011, 60(1): 016802. doi: 10.7498/aps.60.016802
[16]	Jiang Lei, Wang Pei-Ji, Zhang Chang-Wen, Feng Xian-Yang, Lu Yao, Zhang Guo-Lian. Electronic structure and optical properties of Cr doped SnO2 superlattice. Acta Physica Sinica, 2011, 60(9): 093101. doi: 10.7498/aps.60.093101
[17]	Li Zhi-Hua, Wang Wen-Xin, Liu Lin-Sheng, Jiang Zhong-Wei, Gao Han-Chao, Zhou Jun-Ming. As-soak dependence of interface roughness of AlSb/InAs superlattice. Acta Physica Sinica, 2007, 56(3): 1785-1789. doi: 10.7498/aps.56.1785
[18]	Deng Cheng-Liang, Shao Ming-Zhu, Luo Shi-Yu. Interaction between charged particle and strained superlattice and chaotic behaviours of the system. Acta Physica Sinica, 2006, 55(5): 2422-2426. doi: 10.7498/aps.55.2422
[19]	Gu Pei-Fu, Chen Hai-Xing, Qin Xiao-Yun, Liu Xu. Design of polarization band-pass filters based on the theory of thin-film photonic crystal superlattice. Acta Physica Sinica, 2005, 54(2): 773-776. doi: 10.7498/aps.54.773
[20]	Zhang Qi-Yi, Tian Qiang. . Acta Physica Sinica, 2002, 51(8): 1804-1807. doi: 10.7498/aps.51.1804

Catalog

Vol. 73, Issue 11 - 2024-06-05

Metrics

Abstract views: 2520
PDF Downloads: 199
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板