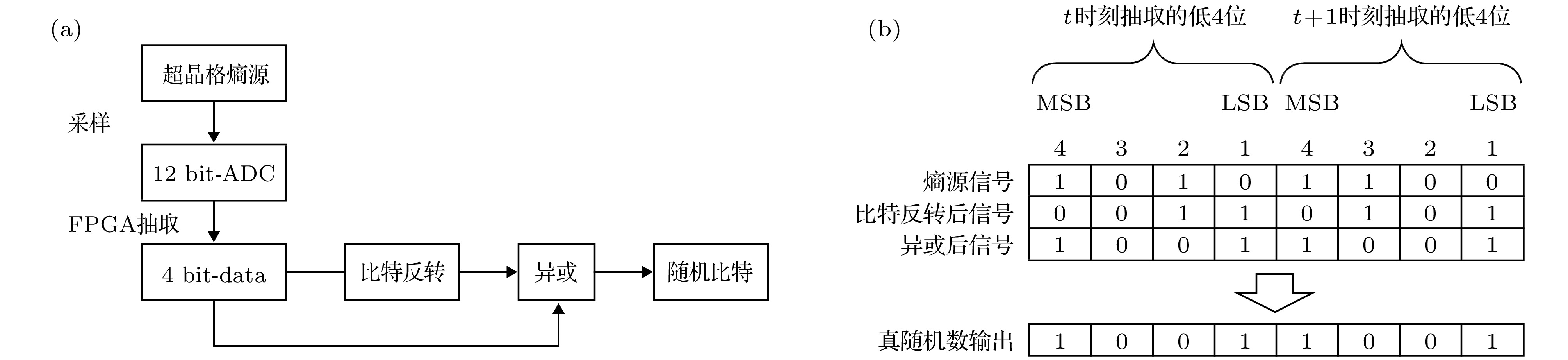
-
物理真随机数发生器对密码学和保密通信至关重要. 现有随机数发生器, 或者复杂庞大, 或者受限于器件带宽, 不能很好地满足现代高速通信系统的需要. 本文提出了一种基于超晶格(superlattices, SLs)芯片的全固态实时高速物理真随机数发生器. 通过选取合适直流偏置电压对SLs芯片进行激发, 从而产生高频混沌振荡信号作为物理熵源, 利用采样频率为2 GHz的多位模数转换器(analog-to-digital converter, ADC)进行量化, 生成12位的二进制随机比特, 然后使用现场可编程逻辑门阵列(field programmable gate array, FPGA)抽取最低4位为有效位并进行比特反转以改善其随机性, 最终获得了实时速率为8 Gbit/s的随机数. 经验证, 该发生器产生的随机数通过了随机数行业标准(NIST SP 800-22)的测试, 具备优良的统计特性, 有望小型化集成到高速通信设备之上.
Secret key is required in secure communications, and random numbers are generally used as keys to encrypt the original information. So it is crucial for cryptography and secure communication to generate the physical random number, which is completely safer than pseudo random number. However, Existing physical random number generator systems are difficult to satisfy the requirements of high-speed communication due to their complexity, large size, and limited equipment bandwidth. The GaAs/Al0.45Ga0.55 superlattices is based on a structure formed by the alternating growth of two semiconductor materials, and has a good low-dimensional structure for studying the nonlinear behavior of electrons. Recent studies have shown that the GaAs/Al0.45Ga0.55 superlattices under the DC voltage could appear chaos current oscillation states in some certain voltage ranges. An all-solid-state real-time high-speed physical true random number generator based on superlattices is presented. The superlattices, excited by appropriate DC bias voltage, could generate a high-frequency chaotic oscillation signal as a source of physical entropy. A multi-bit analog-to-digital converter with 2 GHz sampling frequency is used for quantization to generate 12-bit binary random bits. Then, the field programmable gate array extracts the lowest 4 bits as valid bits and inverts bits to improve its randomness, and finally a true random number with a real-time rate of 8 Gbit/s is obtained. To obtained a superlattices signal with a higher degree of chaos, the Lyapunov exponent was used to assist in selecting a more suitable DC bias. The random number generated by the superlattices, owning excellent statistical characteristics, could pass the test of the random number industry standard (NIST SP 800-22), which is expected to be miniaturized and integrated on high-speed communication equipment. -
Keywords:
- superlattices /
- spontaneous chaotic oscillation /
- physical true random numbers /
- multibitsample
[1] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Oowada I, Kurashige T, Shiki M, Yoshimori S, Yoshimura K, Davis P 2008 Nat. Photonics 2 728
Google Scholar
[2] Karakaya B, Çelik V, Gülten A 2017 Int. J. Circuit Theory Appl. 45 1885
Google Scholar
[3] Shannon C E 1949 Bell Syst. Tech. J. 28 656
Google Scholar
[4] Guo H, Liu Y, Dang A H, Wei W 2009 Chin. Sci. Bull. 54 3651
Google Scholar
[5] Arslan T S, Kaya T 2018 Comput. Math. Methods Med. 2018 3579275
[6] Kim J, Nili H, Truong N D, Ahmed T, Yang J, Jeong D S, Sriram S, Ranasinghe D C, Ippolito S, Chun H, Kavehei O 2019 IEEE Trans. Circuits Syst. I Regul. Pap. 66 2615
Google Scholar
[7] Petrie C S, Connelly J A 2000 IEEE Trans. Circuits Syst. 47 615
Google Scholar
[8] Yamanashi Y, Yoshikawa N 2009 IEEE Trans. Appl. Supercond. 19 630
Google Scholar
[9] 汪鹏君, 李桢, 李刚, 程旭, 张会红 2019 电子学报 47 417
Google Scholar
Wang P j, Li Z, Li G, Cheng X, Zhang H H 2019 Acta Elec. Sin. 47 417
Google Scholar
[10] Chen J X, Ran L, Chen K 2001 J. Electron. 18 56
[11] Pareschi F, Setti G, Rovatti R 2006 Proceedings of the 32nd European Solid-State Circuits Conference Montreaux, Switzerland, September 19−21, 2006 pp130−133
[12] Virte M, Mercier E, Thienpont H, Panajotov K, Sciamanna M 2014 Opt. Express 22 17271
Google Scholar
[13] Kanter I, Aviad Y, Reidler I, Cohen E, Rosenbluh M 2009 Nat. Photonics 4 58
[14] 王龙生, 赵彤, 王大铭, 吴旦昱, 周磊, 武锦, 刘新宇, 王安帮 2017 66 234205
Google Scholar
Wang L S, Zhao T, Wang D M, Wu D Y, Zhou L, Wu J, Liu X Y, Wang A B 2017 Acta Phys. Sin. 66 234205
Google Scholar
[15] 孙媛媛, 李璞, 郭龑强, 郭晓敏, 刘香莲, 张建国, 桑鲁骁, 王云才 2017 66 30503
Sun Y Y, Li P, Guo Y Q, Guo X M, Liu X L, Zhang J G, Sang L X, Wang Y C 2017 Acta Phys. Sin. 66 30503
[16] Esaki L, Chang L L 1974 Phys. Rev. Lett. 33 495
Google Scholar
[17] Zhang Y H, Kastrup J, Klann R, Ploog K H, Grahn H T 1996 Phys. Rev. Lett. 77 3001
Google Scholar
[18] Wu J Q, Jiang D S, Sun B Q 1999 Phys. E 4 137
Google Scholar
[19] Huang Y, Li W, Ma W, Qin H, Zhang Y H 2012 Chin. Sci. Bull. 57 2070
Google Scholar
[20] Barkissy D, Nafidi A, Boutramine A, Benchtaber N, Khalal A, El Gouti T 2016 Appl. Phys. A 123
[21] Huang Y, Qin H, Li W, Lu S, Dong J, Grahn H T, Zhang Y 2014 Europhys. Lett. 105 47005
Google Scholar
[22] Li W, Aviad Y, Reidler I, Song H, Huang Y, Biermann K, Rosenbluh M, Zhang Y, Grahn H T, Kanter I 2015 Europhys. Lett. 1123
[23] Li W, Reidler I, Aviad Y, Huang Y, Song H, Zhang Y, Rosenbluh M, Kanter I 2013 Phys. Rev. Lett. 111 044102
Google Scholar
[24] Grahn H, Kastrup J, Ploog K, Bonilla L, Galán J, Kindelan M, Moscoso M 1995 Jpn. J. Appl. Phys. 34 4526
Google Scholar
[25] Zhang Y, Klann R, Grahn H T, Ploog K H 1997 Superlattices Microstruct. 21 565
Google Scholar
[26] Gettings C, Speake C C 2019 Rev. Sci. Instrum. 90 025004
Google Scholar
[27] Li Y, Ding Y, Li T 2016 Chemom. Intell. Lab. Syst. 156 157
Google Scholar
[28] 谭平安, 张波, 丘东元 2010 59 3747
Google Scholar
Tan P A, Zhang B, Qiu D Y 2010 Acta Phys. Sin. 59 3747
Google Scholar
[29] Liu Y F, Yang D D, Zheng H, Wang L X 2017 Chin. Phys. B 26 120502
[30] Liu Y F, Yang D D, Wang L X, Li Q 2018 Chin. Phys. Lett. 35 046801
[31] Callan K E, Illing L, Gao Z, Gauthier D J, Scholl E 2010 Phys. Rev. Lett. 104 113901
Google Scholar
[32] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
[33] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Physica D 16 285
Google Scholar
[34] Stefánsson A, Končar N, Jones A J 1997 Neural Comput. Appl. 5 131
Google Scholar
[35] Vicente R, Dauden J, Colet P, Toral R 2005 IEEE J. Quantum Electron. 41 541
Google Scholar
[36] Takens F 1981 Dynamical Systems and Turbulence (Heidelberg: Springer Press) pp366−381
[37] Hirano K, Amano K, Uchida A, Naito S, Inoue M, Yoshimori S, Yoshimura K, Davis P 2009 IEEE J. Quantum Electron. 45 1367
Google Scholar
[38] Li N, Kim B, Chizhevsky V N, Locquet A, Bloch M, Citrin D S, Pan W 2014 Opt. Express 22 6634
Google Scholar
[39] Nguimdo R M, Verschaffelt G, Danckaert J, Leijtens X, Bolk J, van der Sande G 2012 Opt. Express 20 28603
Google Scholar
[40] Hirano K, Yamazaki T, Morikatsu S, Okumura H, Aida H, Uchida A, Yoshimori S, Yoshimura K, Harayama T, Davis P 2010 Opt. Express 18 5512
Google Scholar
[41] Li X Z, Chan S C 2012 Opt. Lett 37 2163
Google Scholar
[42] Oliver N, Soriano M C, Sukow D W, Fischer I 2013 IEEE J. Quantum Electron. 49 910
Google Scholar
[43] Sciamanna M, Shore K A 2015 Nat. Photonics 9 151
Google Scholar
[44] Akizawa Y, Yamazaki T, Uchida A, Harayama T, Sunada S, Arai K, Yoshimura K, Davis P 2012 IEEE Photonics Technol. Lett. 24 1042
Google Scholar
[45] 赵东亮, 李璞, 刘香莲, 郭晓敏, 郭龑强, 张建国, 王云才 2017 66 050501
Zhao D L, Li P, Liu X L, Guo X M, Guo Y Q, Zhang J G, Wang Y C 2017 Acta Phys. Sin. 66 050501
-
图 1 超晶格 (a)芯片实物图; (b)结构示意图; (c)能带; (d)高低场畴和级联隧穿模型
Fig. 1. (a) Picture of SLs chip; (b) schematic representation of the SLs device; (c) energy band diagram of SLs; (d) the models of high and low field domain and sequential tunneling of SLs.
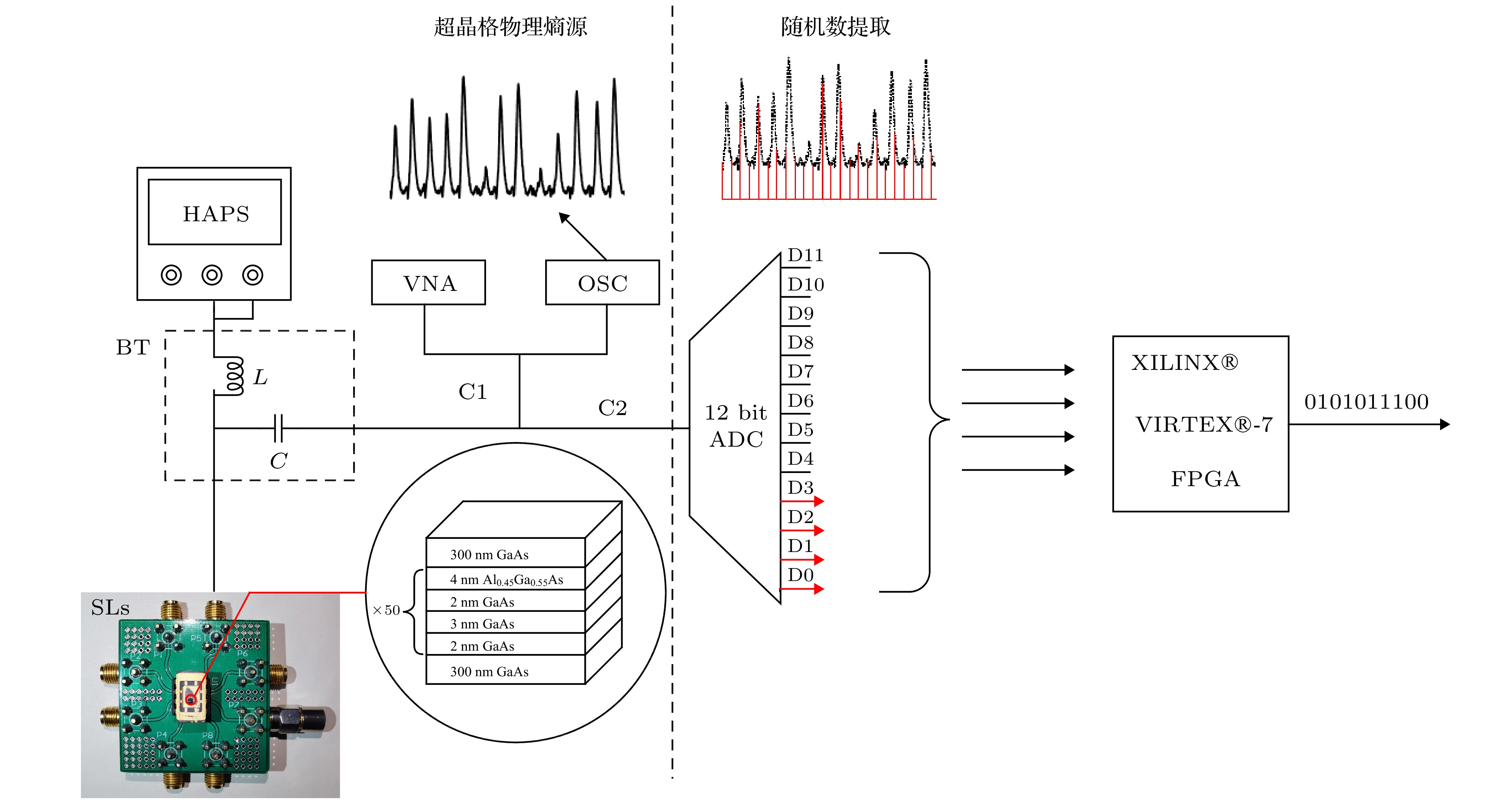
图 2 超晶格高速物理随机数产生装置(HAPS, 高精度电源; BT, T型偏置器; SLs, 超晶格; L, 电感; C, 电容; OSC, 示波器; VNA, 矢量网络分析仪; ADC, 模数转化器; FPGA, 现场可编程逻辑门阵列)
Fig. 2. Schematic for high speed physical random number generator of SLs (HAPS, high accuracy powersupply; BT, Bias-Tee; SLs, superlattices; L, inductance (unit Lenz); C, capacitance; OSC, oscilloscope; VNA, vector network analyzer; ADC, analog digital converter; FPGA, field programmable gate array).
图 4 超晶格 (a)单峰信号时序图; (b)双峰信号时序图; (c)非周期信号时序图; (d) 单峰信号功率谱; (e)双峰信号功率谱; (f)非周期信号功率谱
Fig. 4. Superlattices: (a) Temporal waveform of single peak signal; (b) temporal waveform of bimodal signal; (c) temporal waveform of non-periodic signal; (d) power spectrum of single peak signal; (e) power spectrum of single bimodal signal; (f) power spectrum of single non-periodic signal.
图 6 (a)不同电压下超晶格信号的最大Lyapunov指数; (b)重构相空间
Fig. 6. (a) The maximum Lyapunov exponents of the superlattices signal at different voltages; (b) the phase space of the superlattices signal.
图 7 选取低m位有效的概率密度分布 (a) m = 8; (b) m = 6; (c) m = 5; (d) m = 4
Fig. 7. M-bit effective probability density distribution: (a) m = 8; (b) m = 6; (c) m = 5; (d) m = 4.
图 8 超晶格量化采集方案 (a)采集转化原理图; (b)后处理方案示意图
Fig. 8. acquisition scheme of SLs: (a) Schematic diagram of acquisition conversion; (b) schematic diagram of postprocessing.
图 9 不同LEs的超晶格随机数的NIST测试结果
Fig. 9. Results of NIST for superlatticesrandom numbers at different Les.
表 1 NIST随机特性测试结果
Table 1. Results of NIST statistical test.
统计测试 P 值 通过百分比 结果 频率测试 0.514124 0.995 通过 块内频率测试 0.966244 0.990 通过 累加和测试 0.981609 0.993 通过 游程测试 0.782040 0.993 通过 块内长游程测试 0.657933 0.996 通过 二进制矩阵秩测试 0.379555 0.992 通过 离散傅里叶变换测试 0.196920 0.985 通过 非重叠模块匹配测试 0.938463 0.988 通过 重叠块比配测试 0.224821 0.987 通过 全局通用统计测试 0.513309 0.989 通过 近似熵测试 0.955835 0.998 通过 随机游动测试 0.637119 0.985 通过 随机游动变量测试 0.324180 0.986 通过 串行测试 0.637119 0.982 通过 线性复杂度测试 0.414525 0.995 通过 
下载: 导出CSV
-
[1] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Oowada I, Kurashige T, Shiki M, Yoshimori S, Yoshimura K, Davis P 2008 Nat. Photonics 2 728
Google Scholar
[2] Karakaya B, Çelik V, Gülten A 2017 Int. J. Circuit Theory Appl. 45 1885
Google Scholar
[3] Shannon C E 1949 Bell Syst. Tech. J. 28 656
Google Scholar
[4] Guo H, Liu Y, Dang A H, Wei W 2009 Chin. Sci. Bull. 54 3651
Google Scholar
[5] Arslan T S, Kaya T 2018 Comput. Math. Methods Med. 2018 3579275
[6] Kim J, Nili H, Truong N D, Ahmed T, Yang J, Jeong D S, Sriram S, Ranasinghe D C, Ippolito S, Chun H, Kavehei O 2019 IEEE Trans. Circuits Syst. I Regul. Pap. 66 2615
Google Scholar
[7] Petrie C S, Connelly J A 2000 IEEE Trans. Circuits Syst. 47 615
Google Scholar
[8] Yamanashi Y, Yoshikawa N 2009 IEEE Trans. Appl. Supercond. 19 630
Google Scholar
[9] 汪鹏君, 李桢, 李刚, 程旭, 张会红 2019 电子学报 47 417
Google Scholar
Wang P j, Li Z, Li G, Cheng X, Zhang H H 2019 Acta Elec. Sin. 47 417
Google Scholar
[10] Chen J X, Ran L, Chen K 2001 J. Electron. 18 56
[11] Pareschi F, Setti G, Rovatti R 2006 Proceedings of the 32nd European Solid-State Circuits Conference Montreaux, Switzerland, September 19−21, 2006 pp130−133
[12] Virte M, Mercier E, Thienpont H, Panajotov K, Sciamanna M 2014 Opt. Express 22 17271
Google Scholar
[13] Kanter I, Aviad Y, Reidler I, Cohen E, Rosenbluh M 2009 Nat. Photonics 4 58
[14] 王龙生, 赵彤, 王大铭, 吴旦昱, 周磊, 武锦, 刘新宇, 王安帮 2017 66 234205
Google Scholar
Wang L S, Zhao T, Wang D M, Wu D Y, Zhou L, Wu J, Liu X Y, Wang A B 2017 Acta Phys. Sin. 66 234205
Google Scholar
[15] 孙媛媛, 李璞, 郭龑强, 郭晓敏, 刘香莲, 张建国, 桑鲁骁, 王云才 2017 66 30503
Sun Y Y, Li P, Guo Y Q, Guo X M, Liu X L, Zhang J G, Sang L X, Wang Y C 2017 Acta Phys. Sin. 66 30503
[16] Esaki L, Chang L L 1974 Phys. Rev. Lett. 33 495
Google Scholar
[17] Zhang Y H, Kastrup J, Klann R, Ploog K H, Grahn H T 1996 Phys. Rev. Lett. 77 3001
Google Scholar
[18] Wu J Q, Jiang D S, Sun B Q 1999 Phys. E 4 137
Google Scholar
[19] Huang Y, Li W, Ma W, Qin H, Zhang Y H 2012 Chin. Sci. Bull. 57 2070
Google Scholar
[20] Barkissy D, Nafidi A, Boutramine A, Benchtaber N, Khalal A, El Gouti T 2016 Appl. Phys. A 123
[21] Huang Y, Qin H, Li W, Lu S, Dong J, Grahn H T, Zhang Y 2014 Europhys. Lett. 105 47005
Google Scholar
[22] Li W, Aviad Y, Reidler I, Song H, Huang Y, Biermann K, Rosenbluh M, Zhang Y, Grahn H T, Kanter I 2015 Europhys. Lett. 1123
[23] Li W, Reidler I, Aviad Y, Huang Y, Song H, Zhang Y, Rosenbluh M, Kanter I 2013 Phys. Rev. Lett. 111 044102
Google Scholar
[24] Grahn H, Kastrup J, Ploog K, Bonilla L, Galán J, Kindelan M, Moscoso M 1995 Jpn. J. Appl. Phys. 34 4526
Google Scholar
[25] Zhang Y, Klann R, Grahn H T, Ploog K H 1997 Superlattices Microstruct. 21 565
Google Scholar
[26] Gettings C, Speake C C 2019 Rev. Sci. Instrum. 90 025004
Google Scholar
[27] Li Y, Ding Y, Li T 2016 Chemom. Intell. Lab. Syst. 156 157
Google Scholar
[28] 谭平安, 张波, 丘东元 2010 59 3747
Google Scholar
Tan P A, Zhang B, Qiu D Y 2010 Acta Phys. Sin. 59 3747
Google Scholar
[29] Liu Y F, Yang D D, Zheng H, Wang L X 2017 Chin. Phys. B 26 120502
[30] Liu Y F, Yang D D, Wang L X, Li Q 2018 Chin. Phys. Lett. 35 046801
[31] Callan K E, Illing L, Gao Z, Gauthier D J, Scholl E 2010 Phys. Rev. Lett. 104 113901
Google Scholar
[32] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
[33] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Physica D 16 285
Google Scholar
[34] Stefánsson A, Končar N, Jones A J 1997 Neural Comput. Appl. 5 131
Google Scholar
[35] Vicente R, Dauden J, Colet P, Toral R 2005 IEEE J. Quantum Electron. 41 541
Google Scholar
[36] Takens F 1981 Dynamical Systems and Turbulence (Heidelberg: Springer Press) pp366−381
[37] Hirano K, Amano K, Uchida A, Naito S, Inoue M, Yoshimori S, Yoshimura K, Davis P 2009 IEEE J. Quantum Electron. 45 1367
Google Scholar
[38] Li N, Kim B, Chizhevsky V N, Locquet A, Bloch M, Citrin D S, Pan W 2014 Opt. Express 22 6634
Google Scholar
[39] Nguimdo R M, Verschaffelt G, Danckaert J, Leijtens X, Bolk J, van der Sande G 2012 Opt. Express 20 28603
Google Scholar
[40] Hirano K, Yamazaki T, Morikatsu S, Okumura H, Aida H, Uchida A, Yoshimori S, Yoshimura K, Harayama T, Davis P 2010 Opt. Express 18 5512
Google Scholar
[41] Li X Z, Chan S C 2012 Opt. Lett 37 2163
Google Scholar
[42] Oliver N, Soriano M C, Sukow D W, Fischer I 2013 IEEE J. Quantum Electron. 49 910
Google Scholar
[43] Sciamanna M, Shore K A 2015 Nat. Photonics 9 151
Google Scholar
[44] Akizawa Y, Yamazaki T, Uchida A, Harayama T, Sunada S, Arai K, Yoshimura K, Davis P 2012 IEEE Photonics Technol. Lett. 24 1042
Google Scholar
[45] 赵东亮, 李璞, 刘香莲, 郭晓敏, 郭龑强, 张建国, 王云才 2017 66 050501
Zhao D L, Li P, Liu X L, Guo X M, Guo Y Q, Zhang J G, Wang Y C 2017 Acta Phys. Sin. 66 050501
下载:
计量
- 文章访问数: 6982
- PDF下载量: 88
- 被引次数: 0
