-
Indium phosphide (InP) material hasmany advantages, such as large band gap, high electron mobility, high photoelectric conversion efficiency, high temperature resistance, and radiation resistance, which is superior to silicon (Si) and gallium arsenide (GaAs). Meanwhile InP is widely used in optical communication, high-frequency millimeter waves, optoelectronic integrated circuits, satellite communication, space solar cells, and other fields. Radiation particles incident on InP device can generate displacement atoms inside the device through elastic processes. And these displacement atoms continue cascade collisions to generate lattice defects which are vacancies, interstitials, and clusters. These defects capture electrons-holes by defective energy levels in the energy band, and then resulting in a decrease in the life of minority carriers which is the reason of degradation of InP devices. The process of degradation of InP device, induced by lattice defects from ion-irradiation, is called displacement damage effect (DDE). The non-ionizing loss energy (NIEL) scaling is a useful method to predict the degradation of device caused by DDE of radiation particles. Many studies have shown that the NIEL is linearly related to the damage coefficient of InP device. Previous studies of radiation damage effect of InP device mainly focused on single-energy protons, electrons, and neutrons. Of the particles in low earth orbit (LEO),the vast majority of particles are protons, with a few being α particles and electrons, while the electron’s NIEL is too small and its DDE is negligible. The InP’s NIEL induced by proton and α energy in LEO has not been studied in detail. Therefore, this paper uses Monte Carlo software Geant4 to study the NIEL, damage energy distribution with depth, and annual total non-ionization loss energy generated by protons and α particles in LEO in 500/1000/5000 μm InP materials. The shielding of 150-μm-thick SiO2 layer and 2.54-mm-thick Al layer from protons and α particles are used as InP solar cell and InP devices in spacecraft, respectively. It is found that the energy spectrum determines the non-ionizing damage energy
$ {T}_{\text{dam}} $ distribution, and then influences the NIEL value: the NIEL value increases with$ {T}_{\text{dam}} $ increasing and thickness of InP material decreasing. And α NIEL is larger than proton’s, the single particle DDE of InP device, induced by α particles, should be concerned. The annual non-ionizing damage energy of proton accounts for 98%, which means that proton is the main factor degrading InP devices in LEO.-
Keywords:
- InP /
- displacement damage /
- Geant4 /
- non-ionizing loss energy /
- low Earth orbit
[1] Sun S X, Ji H F, Yao H J, Li S, Jin Z, Ding P, Zhong Y H 2016 Chin. Phys. B 25 4
Google Scholar
[2] Shatalov A, Subramanian S, Klein A 2001 IEEE Trans. Nucl. Sci. 48 2262
Google Scholar
[3] Yamaguchi M, Takamoto T, Taylor S J, Walters R J, Summers G P, Flood D J, Ohmori M 1997 J. Appl. Phys. 81 6013
Google Scholar
[4] Srour J R, Palko J W 2013 IEEE Trans. Nucl. Sci. 60 1740
Google Scholar
[5] Jay A, Hemeryck A, Richard N, Martin-Samos L, Raine M, Le Roch A, Mousseau N, Goiffon V, Paillet P, Gaillardin M, Magnan P 2018 IEEE Trans. Nucl. Sci. 65 724
Google Scholar
[6] Nordlund K, Zinkle S J, Sand A E, Granberg F, Averback R S, Stoller R E, Suzudo T, Malerba L, Banhart F, Weber W J, Willaime F, Dudarev S L, Simeone D 2018 J. Nucl. Mater. 512 450
Google Scholar
[7] Summers G P, Burke E A, Shapiro P, Messenger S R, Walters R J 1993 IEEE Trans. Nucl. Sci. 40 1372
Google Scholar
[8] Messenger S R, Burke E A, Summers G P, Xapsos M A, Walters R J, Jackson E M, Weaver B D 1999 IEEE Trans. Nucl. Sci. 46 1595
Google Scholar
[9] Srour J R, Marshall C J, Marshall P W 2003 IEEE Trans. Nucl. Sci. 50 653
Google Scholar
[10] Li C H, Lu H L, Zhang Y M, Liu M, Zhao X H 2015 IEEE Trans. Nucl. Sci. 62 1336
Google Scholar
[11] 白雨蓉, 李永宏, 刘方, 廖文龙, 何欢, 杨卫涛, 贺朝会 2021 70 172401
Google Scholar
Bai Y R, Li Y H, Liu F, Liao W L, He H, Yang W T, He C H 2021 Acta Phys. Sin. 70 172401
Google Scholar
[12] 李薇, 白雨蓉, 郭昊轩, 贺朝会, 李永宏 2022 71 082401
Google Scholar
Li W, Bai Y R, Guo H X, He C H, Li Y H 2022 Acta Phys. Sin. 71 082401
Google Scholar
[13] Akkerman A, Barak J 2006 IEEE Trans. Nucl. Sci. 53 3667
Google Scholar
[14] Akkerman A, Barak J 2007 Nucl. Instrum. Meth. B 260 529
Google Scholar
[15] Insoo J, Xapsos M A, Messenger S R, Burke E A, Walters R J, Summers G P, Jordan T 2003 IEEE Trans. Nucl. Sci. 50 1924
Google Scholar
[16] Agostinelli S, Allison J, Amako K, et al. 2003 Nucl. Instrum. Meth. A 506 250
Google Scholar
[17] Liu L, Mei B, Zheng Z S, Wang L, Bai Y R, Yu Q K, Li P, Zhao H D, Sun Y C, Li B 2023 IEEE Trans. Nucl. Sci. 70 1885
Google Scholar
[18] Xie F, Zang H, Liu F, He H, Liao W L, Huang Y 2020 Acta Phys. Sin. 69 192401
Google Scholar
[19] Messenger S R, Burke E A, Xapsos M A, Summers G P, Walters R J, Insoo Jun, Jordan T 2003 IEEE Trans. Nucl. Sci. 50 1919
Google Scholar
[20] Dietrich W F, Shea M A, Smart D F 1997 IEEE T. Nucl. Sci. 44 2150
Google Scholar
-
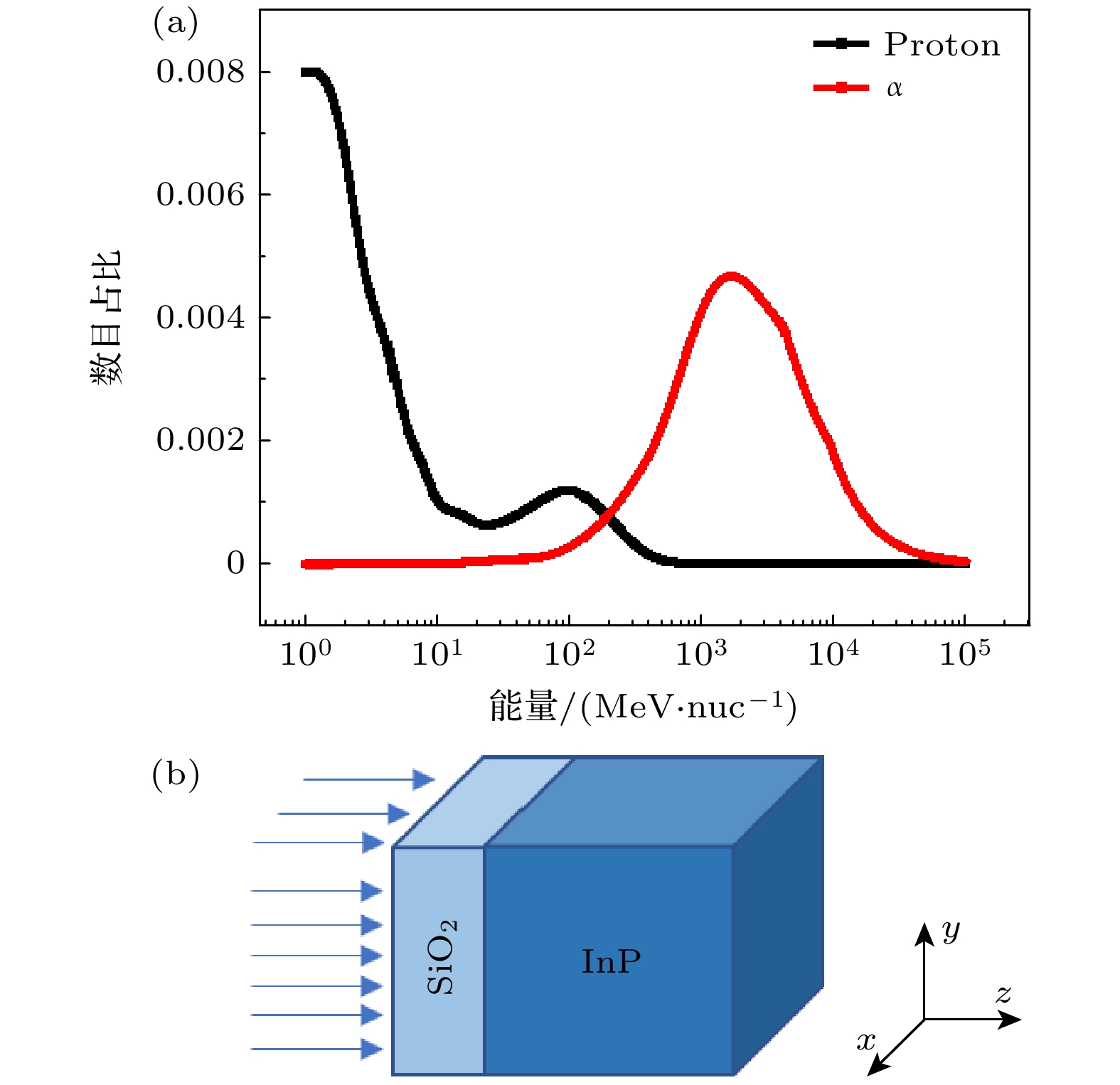
图 2 InP太阳能电池工况模拟设置图 (a)近地轨道内质子和α粒子能谱; (b) InP太阳能电池模拟结构图, 即500 μm×500 μm区域源离子入射500/1000/5000 μm InP材料(深蓝色)经过150 μm SiO2(浅蓝色)后的示意图
Figure 2. The simulation settings of InP solar cell: (a) Proton and α energy spectrum in low Earth orbit; (b) simulation structure diagram of InP solar cells, the schematic of 500 μm×500 μm area source ion-incident 500/1000/5000 μm InP materials (deep blue) after 150 μm SiO2 (light blue)
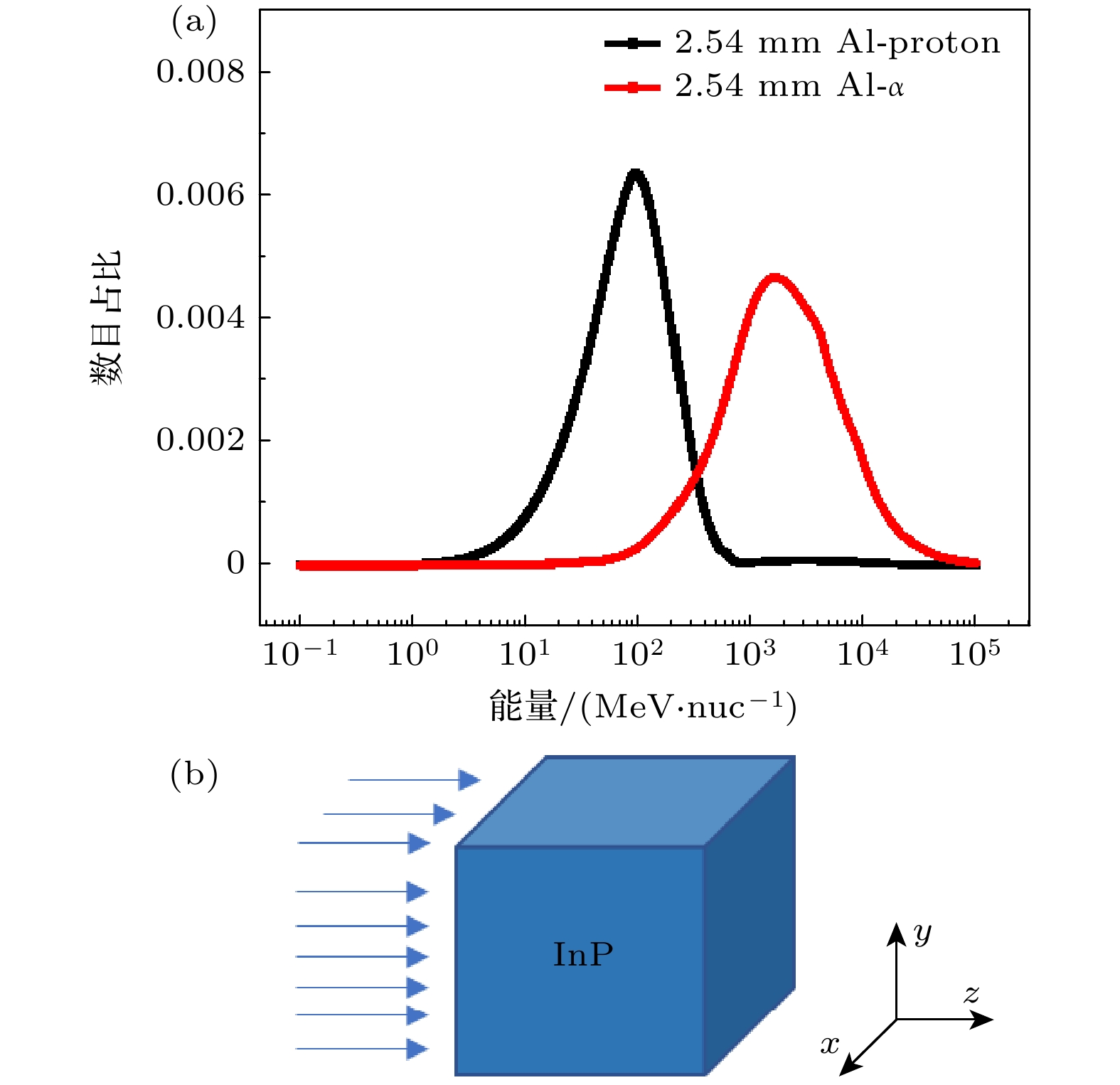
图 3 航天器内部InP电子器件工况模拟设置图 (a)近地轨道内经过2.54 mm铝层屏蔽的质子和α粒子能谱; (b) InP材料模拟结构图, 即500 μm×500 μm区域源离子入射500/1000/5000 μm InP材料
Figure 3. The simulation settings of InP electronics in spacecraft: (a) Proton and α energy spectrum after the shielding of 2.54 mm Al in low Earth orbit; (b) simulation structure diagram of InP solar cells, the schematic of 500 μm×500 μm area source ion-incident 500/1000/5000 μm InP materials.
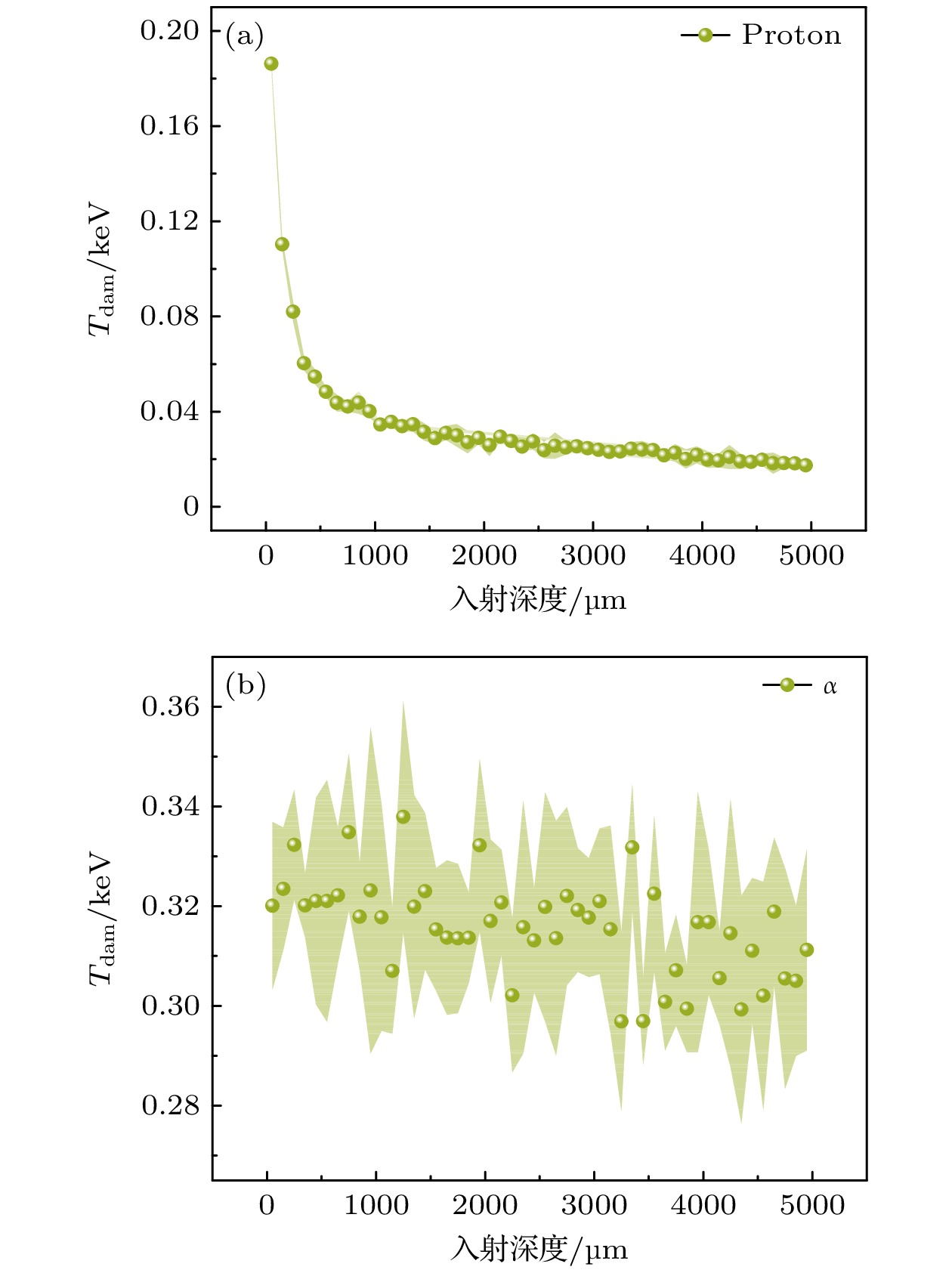
图 4 近地轨道内质子和α粒子经过150 μm SiO2屏蔽后入射5000 μm InP中产生的$ {T}_{\text{dam}} $随深度分布, 数值的阴影是通过10次模拟计算得出的标准偏差
Figure 4. The distribution of $ {T}_{\text{dam}} $with depth of 5000 μm InP materials induced by proton and α in low Earth orbit after the shielding of 150 μm SiO2. The shadow of values is standard deviation which is calculated by ten simulations.
图 5 近地轨道内质子和α粒子经过2.54 mm铝层后在5000 μm InP中产生的$ {T}_{\text{dam}} $随深度分布, 数值的阴影是通过10次模拟计算得出的标准偏差
Figure 5. The distribution of $ {T}_{\text{dam}} $ with depth of 5000 μm InP materials induced by proton and α in low Earth orbit after the shielding of 2.54 mm Al. The shadow of values is standard deviation which is calculated by ten simulations.
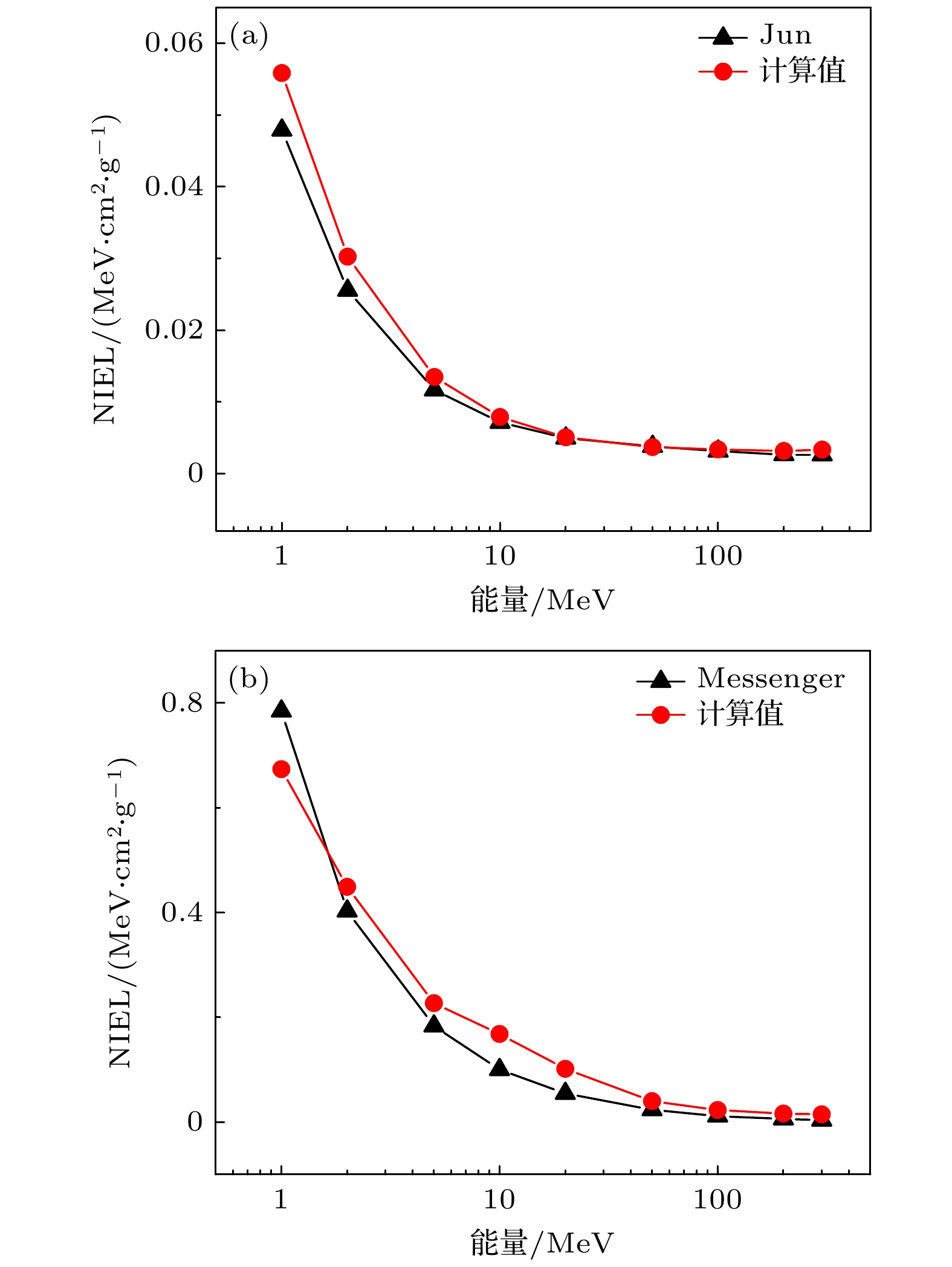
表 1 近地轨道质子及α粒子经过150 μm SiO2后在InP产生的NIEL统计表
Table 1. NIEL of InP induced by proton and α in low Earth orbit after the shielding of 150 μm SiO2.
粒子种类 厚度/μm NIEL/(MeV·cm2·g–1) 离散系数 质子 500 0.00219 0.01023 1000 0.00159 0.01381 5000 0.00075 0.01017 α 500 0.00705 0.02649 1000 0.00697 0.01609 5000 0.00691 0.00797 
DownLoad: CSV
表 2 近地轨道质子及α粒子经过2.54 mm 铝层后在InP产生的NIEL统计表
Table 2. NIEL of InP induced by proton and α in low Earth orbit after the shielding of 2.54 mm Al.
粒子种类 厚度/μm NIEL/(MeV·cm2·g–1) 离散系数 质子 500 0.00403 0.00511 1000 0.00387 0.00554 5000 0.00300 0.00840 α 500 0.00704 0.01135 1000 0.00702 0.00505 5000 0.00689 0.00290
DownLoad: CSV
表 3 不同屏蔽材料下近地轨道的质子和α粒子在500 μm InP中产生的年总非电离损伤能汇总
Table 3. Annual non-ionizing damage energy and percent of proton and α in low Earth orbit after the shielding of 150 μm SiO2 and 2.54 mm Al in 500 μm InP materials
屏蔽材料 入射粒子 粒子数目 总非电离损伤能/MeV 占比/% 150 μm SiO2 质子 53395886 26452.04 98.73 α 222307 339.85 1.27 2.54 mm 铝 质子 94458945 86520.48 99.58 α 219853 365.77 0.42
DownLoad: CSV
-
[1] Sun S X, Ji H F, Yao H J, Li S, Jin Z, Ding P, Zhong Y H 2016 Chin. Phys. B 25 4
Google Scholar
[2] Shatalov A, Subramanian S, Klein A 2001 IEEE Trans. Nucl. Sci. 48 2262
Google Scholar
[3] Yamaguchi M, Takamoto T, Taylor S J, Walters R J, Summers G P, Flood D J, Ohmori M 1997 J. Appl. Phys. 81 6013
Google Scholar
[4] Srour J R, Palko J W 2013 IEEE Trans. Nucl. Sci. 60 1740
Google Scholar
[5] Jay A, Hemeryck A, Richard N, Martin-Samos L, Raine M, Le Roch A, Mousseau N, Goiffon V, Paillet P, Gaillardin M, Magnan P 2018 IEEE Trans. Nucl. Sci. 65 724
Google Scholar
[6] Nordlund K, Zinkle S J, Sand A E, Granberg F, Averback R S, Stoller R E, Suzudo T, Malerba L, Banhart F, Weber W J, Willaime F, Dudarev S L, Simeone D 2018 J. Nucl. Mater. 512 450
Google Scholar
[7] Summers G P, Burke E A, Shapiro P, Messenger S R, Walters R J 1993 IEEE Trans. Nucl. Sci. 40 1372
Google Scholar
[8] Messenger S R, Burke E A, Summers G P, Xapsos M A, Walters R J, Jackson E M, Weaver B D 1999 IEEE Trans. Nucl. Sci. 46 1595
Google Scholar
[9] Srour J R, Marshall C J, Marshall P W 2003 IEEE Trans. Nucl. Sci. 50 653
Google Scholar
[10] Li C H, Lu H L, Zhang Y M, Liu M, Zhao X H 2015 IEEE Trans. Nucl. Sci. 62 1336
Google Scholar
[11] 白雨蓉, 李永宏, 刘方, 廖文龙, 何欢, 杨卫涛, 贺朝会 2021 70 172401
Google Scholar
Bai Y R, Li Y H, Liu F, Liao W L, He H, Yang W T, He C H 2021 Acta Phys. Sin. 70 172401
Google Scholar
[12] 李薇, 白雨蓉, 郭昊轩, 贺朝会, 李永宏 2022 71 082401
Google Scholar
Li W, Bai Y R, Guo H X, He C H, Li Y H 2022 Acta Phys. Sin. 71 082401
Google Scholar
[13] Akkerman A, Barak J 2006 IEEE Trans. Nucl. Sci. 53 3667
Google Scholar
[14] Akkerman A, Barak J 2007 Nucl. Instrum. Meth. B 260 529
Google Scholar
[15] Insoo J, Xapsos M A, Messenger S R, Burke E A, Walters R J, Summers G P, Jordan T 2003 IEEE Trans. Nucl. Sci. 50 1924
Google Scholar
[16] Agostinelli S, Allison J, Amako K, et al. 2003 Nucl. Instrum. Meth. A 506 250
Google Scholar
[17] Liu L, Mei B, Zheng Z S, Wang L, Bai Y R, Yu Q K, Li P, Zhao H D, Sun Y C, Li B 2023 IEEE Trans. Nucl. Sci. 70 1885
Google Scholar
[18] Xie F, Zang H, Liu F, He H, Liao W L, Huang Y 2020 Acta Phys. Sin. 69 192401
Google Scholar
[19] Messenger S R, Burke E A, Xapsos M A, Summers G P, Walters R J, Insoo Jun, Jordan T 2003 IEEE Trans. Nucl. Sci. 50 1919
Google Scholar
[20] Dietrich W F, Shea M A, Smart D F 1997 IEEE T. Nucl. Sci. 44 2150
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1861
- PDF Downloads: 69
- Cited By: 0
