-
Continuous variable quantum secret sharing protocol can guarantee the unconditional security of secret key information based on the fundamental laws of physics. However, the state preparation operation may become non-ideal and imperfect in practical continuous variable quantum secret sharing scheme, which will introduce additional excess noise and affect the security of the scheme. Therefore, it is necessary to analyze it. We propose a practical continuous variable quantum secret sharing protocol based on imperfect state preparation. Specifically, in the proposed scheme, we assume that there are multiple users, and the imperfect state preparation performed by any user is equivalent to the corresponding untrusted third party using a phase insensitive amplifier to amplify the ideal modulator and laser owned by the user. The equivalent excess noise introduced by the imperfect state preparation can be calculated comprehensively and quantitatively through the gain of the corresponding phase insensitive amplifier. The results show that the continuous variable quantum secret sharing scheme is sensitive to the excess noise introduced by the imperfect state preparation operation, which will inevitably reduce its performance and security. Fortunately, the upper bound of the additional excess noise tolerance for the imperfect state preparation is achieved by using the specific gain formula of the phase insensitive amplifier, thus the security risks caused by the imperfect state preparation can be effectively solved. Due to considering the additional excess noise introduced by imperfect state preparation, tighter secret key rate curves can be obtained by the proposed scheme than those by the ideal continuous variable quantum secret sharing protocol. These results indicate that the proposed scheme can improve the practical security of continuous variable quantum secret sharing scheme, and provide a theoretical basis for its practical applications.
[1] Liu H, Jiang C, Zhu H T, Zou M, Yu Z W, Hu X L, Xu H, Ma S, Han Z, Chen J P, Dai Y, Tang S B, Zhang W, Li H, You L, Wang Z, Hua Y, Hu H, Zhang H, Zhou F, Zhang Q, Wang X B, Chen T Y, Pan J W 2021 Phys. Rev. Lett. 126 250502
Google Scholar
[2] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[3] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shaari J S, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photon. 12 1012
Google Scholar
[4] Wang S, Yin Z Q, He D Y, Chen W, Wang R Q, Ye P, Zhou Y, Fan-Yuan G J, Wang F X, Chen W, Zhu Y G, Morozov P V, Divochiy A V, Zhou Z, Guo G C, Han Z F 2022 Nat. Photon. 16 154
Google Scholar
[5] Yin J, Li Y H, Liao S K, Yang M, Cao Y, Zhang L, Ren J G, Cai W Q, Liu W Y, Li S L, Shu R, Huang Y M, Deng L, Li L, Zhang Q, Liu N L, Chen Y A, Lu C Y, Wang X B, Xu F H, Wang J Y, Peng C Z, Ekert A K, Pan J W 2020 Nature 582 501
Google Scholar
[6] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Han Z Y, Ma S Z, Hu X L, Li Y H, Liu H, Zhou F, Jiang H F, Chen T Y, Li H, You L X, Wang Z, Wang X B, Zhang Q, Pan J W 2021 Nat. Photon. 15 570
Google Scholar
[7] Wang S, He D Y, Yin Z Q, Lu F Y, Cui C H, Chen W, Zhou Z, Guo G C, Han Z F 2019 Phys. Rev. X 9 021046
[8] Liu W Z, Zhang Y Z, Zhen Y Z, Li M H, Liu Y, Fan J , Xu F, Zhang Q, Pan J W 2022 Phys. Rev. Lett. 129 050502
[9] 吴晓东, 黄端, 黄鹏, 郭迎 2022 71 240304
Google Scholar
Wu X D, Huang D, Huang P, Guo Y 2022 Acta Phys. Sin. 71 240304
Google Scholar
[10] Wu X D, Wang Y J, Zhong H, Liao Q, Guo Y 2019 Front. Phys. 14 41501
Google Scholar
[11] 钟海, 叶炜, 吴晓东, 郭迎 2021 70 020301
Google Scholar
Zhong H, Ye W, Wu X D, Guo Y 2021 Acta Phys. Sin. 70 020301
Google Scholar
[12] Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902
Google Scholar
[13] Huang D, Huang P, Lin D , Zeng G 2016 Sci. Rep. 6 19201
[14] Zhang Y, Chen Z, Pirandola S, Wang X, Zhou C, Chu B, Zhao Y, Xu B, Yu S, Guo H 2020 Phys. Rev. Lett. 125 010502
Google Scholar
[15] Grosshans F, Assche G V, Wenger J, Brouri R, Cerf N J, Grangier P 2003 Nature (London) 421 238
Google Scholar
[16] Leverrier A 2015 Phys. Rev. Lett. 114 070501
Google Scholar
[17] Laudenbach F, Pacher C, Fung C H F, Poppe A, Peev M, Schrenk B, Hentschel M, Walther P, Hübel H 2018 Adv. Quantum Technol. 1 1800011
Google Scholar
[18] Leverrier A 2017 Phys. Rev. Lett. 118 200501
Google Scholar
[19] Chen Z, Zhang Y, Wang G, Li Z, Guo H 2018 Phys. Rev. A 98 012314
Google Scholar
[20] Qi B, Evans P G, Grice W P 2018 Phys. Rev. A 97 012317
Google Scholar
[21] Qi B, Gunther H, Evans P G, Williams B P, Camacho R M, Peters N A 2020 Phys. Rev. Appl. 13 054065
Google Scholar
[22] Huang P, Wang T, Chen R, Wang P, Zhou Y, Zeng G 2021 New J. Phys. 23 113028
Google Scholar
[23] Wu X, Wang Y, Guo Y, Zhong H, Huang D 2021 Phys. Rev. A 103 032604
Google Scholar
[24] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829
Google Scholar
[25] Kogias I, Xiang Y, He Q Y, Adesso G 2017 Phys. Rev. A 95 012315
Google Scholar
[26] Schmid C, Trojek P, Bourennane M, Kurtsiefer C, Zukowski M, Weinfurter H 2005 Phys. Rev. Lett. 95 230505
Google Scholar
[27] He G P 2007 Phys. Rev. Lett. 98 028901
Google Scholar
[28] Schmid C, Trojek P, Bourennane M, Kurtsiefer C, Zukowski M, Weinfurter H 2007 Phys. Rev. Lett. 98 028902
Google Scholar
[29] He G P, Wang Z D 2010 Quantum Inf. Comput. 10 28
[30] Grice W P, Qi B 2019 Phys. Rev. A 100 022339
Google Scholar
[31] Wu X , Wang Y, Huang D 2020 Phys. Rev. A 101 022301
Google Scholar
[32] Liao Q, Liu H, Zhu L, Guo Y 2021 Phys. Rev. A 103 032410
Google Scholar
[33] Liu W, Wang X, Wang N, Du S, Li Y 2017 Phys. Rev. A 96 042312
Google Scholar
[34] Shen Y, Yang J, Guo H 2009 J. Phys. B: At. Mol. Opt. Phys. 42 235506
Google Scholar
[35] Usenko V C, Filip R 2010 Phys. Rev. A 81 022318
Google Scholar
[36] Jouguet P, Kunz J S, Diamanti E, Leverrier A 2012 Phys. Rev. A 86 032309
Google Scholar
[37] Fossier S, Diamanti E, Debuisschert T, Tualle-Brouri R, Grangier P 2009 J. Phys. B: At. Mol. Opt. Phys. 42 114014
Google Scholar
[38] Diamanti E, Leverrier A 2015 Entropy 17 6072
Google Scholar
[39] Lodewyck J, Bloch M, García-Patrón R, Fossier S, Karpov E, Diamanti E, Debuisschert T, Cerf N J, Tualle-Brouri R, McLaughlin S W, Grangier P 2007 Phys. Rev. A 76 042305
Google Scholar
[40] Huang P, He G Q, Zeng G H 2013 Int. J. Theor. Phys. 52 1572
Google Scholar
[41] Huang D, Huang P, Wang T, Li H, Zhou Y, Zeng G 2016 Phys. Rev. A 94 032305
Google Scholar
[42] Zhang H, Fang J, He G 2012 Phys. Rev. A 86 022338
Google Scholar
[43] Pirandola S, Laurenza R, Ottaviani C, Banchi L 2017 Nat. Commun. 8 15043
Google Scholar
-
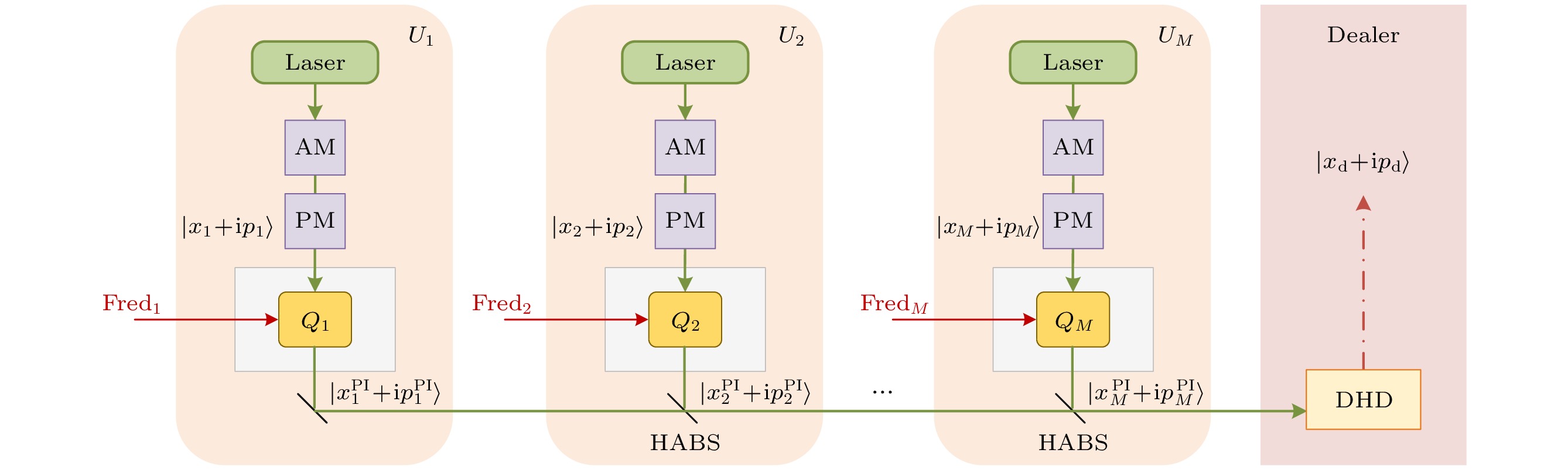
图 1 基于非理想量子态制备的实际CV-QSS方案. AM为振幅调制器, PM为相位调制器, DHD为共扼零差探测, HABS为高度非对称分束器, ${Q_s}{\text{ (}}s = 1, {\text{ 2, }} \cdots {, }M)$表示第$s$个用户${U_s}$处的相位非敏感放大器
Figure 1. Practical CV-QSS scheme based on imperfect quantum state preparation. AM, amplitude modulator; PM, phase modulator; DHD, double homodyne detection; HABS, highly asymmetric beam splitter; ${Q_s}{\text{ (}}s = 1, {\text{ 2, }} \cdots {, }M)$, phase insensitive amplifier at the s-th user.
图 2 基于非理想量子态制备的CV-QSS制备-测量方案图. QM为量子存储器, $T$表示非可信信道的透过率, ${\chi _{{\text{line}}}}$表示信道附加噪声
Figure 2. Schematic diagram of the prepare-and-measure (PM) model of the practical CV-QSS scheme based on imperfect quantum state preparation. QM, quantum memory; $T$, transmission efficiency; ${\chi _{{\text{line}}}}$, channel-added noise.
图 3 基于非理想量子态制备的CV-QSS纠缠模型方案图
Figure 3. Schematic diagram of the entanglement-based (EB) model of the practical CV-QSS scheme based on imperfect quantum state preparation.
图 4 所提出方案的密钥率与调制方差的关系 (a) 不同传输距离$L$; (b) 不同用户数量$M$
Figure 4. The relationship between the secret key rate of the proposed scheme and the modulation variance under: (a) Different transmission distance $L$; (b) different numbers of users $M$.
图 5 所提出方案的密钥率与传输距离的关系 (a) $g = 1$; (b) $g = 1.001$; (c) $g = 1.002$; (d) $g = 1.003$
Figure 5. The relationship between the secret key rate of the proposed scheme and the transmission distance: (a) $g = 1$; (b) $g = $$ 1.001$; (c) $g = 1.002$; (d) $g = 1.003$.
图 6 在不同传输距离$L$下, 所提出方案的密钥率与增益参数$g$的关系
Figure 6. The relationship between the secret key rate of the proposed scheme and the gain g under different transmission distances $L$.
-
[1] Liu H, Jiang C, Zhu H T, Zou M, Yu Z W, Hu X L, Xu H, Ma S, Han Z, Chen J P, Dai Y, Tang S B, Zhang W, Li H, You L, Wang Z, Hua Y, Hu H, Zhang H, Zhou F, Zhang Q, Wang X B, Chen T Y, Pan J W 2021 Phys. Rev. Lett. 126 250502
Google Scholar
[2] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[3] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shaari J S, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photon. 12 1012
Google Scholar
[4] Wang S, Yin Z Q, He D Y, Chen W, Wang R Q, Ye P, Zhou Y, Fan-Yuan G J, Wang F X, Chen W, Zhu Y G, Morozov P V, Divochiy A V, Zhou Z, Guo G C, Han Z F 2022 Nat. Photon. 16 154
Google Scholar
[5] Yin J, Li Y H, Liao S K, Yang M, Cao Y, Zhang L, Ren J G, Cai W Q, Liu W Y, Li S L, Shu R, Huang Y M, Deng L, Li L, Zhang Q, Liu N L, Chen Y A, Lu C Y, Wang X B, Xu F H, Wang J Y, Peng C Z, Ekert A K, Pan J W 2020 Nature 582 501
Google Scholar
[6] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Han Z Y, Ma S Z, Hu X L, Li Y H, Liu H, Zhou F, Jiang H F, Chen T Y, Li H, You L X, Wang Z, Wang X B, Zhang Q, Pan J W 2021 Nat. Photon. 15 570
Google Scholar
[7] Wang S, He D Y, Yin Z Q, Lu F Y, Cui C H, Chen W, Zhou Z, Guo G C, Han Z F 2019 Phys. Rev. X 9 021046
[8] Liu W Z, Zhang Y Z, Zhen Y Z, Li M H, Liu Y, Fan J , Xu F, Zhang Q, Pan J W 2022 Phys. Rev. Lett. 129 050502
[9] 吴晓东, 黄端, 黄鹏, 郭迎 2022 71 240304
Google Scholar
Wu X D, Huang D, Huang P, Guo Y 2022 Acta Phys. Sin. 71 240304
Google Scholar
[10] Wu X D, Wang Y J, Zhong H, Liao Q, Guo Y 2019 Front. Phys. 14 41501
Google Scholar
[11] 钟海, 叶炜, 吴晓东, 郭迎 2021 70 020301
Google Scholar
Zhong H, Ye W, Wu X D, Guo Y 2021 Acta Phys. Sin. 70 020301
Google Scholar
[12] Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902
Google Scholar
[13] Huang D, Huang P, Lin D , Zeng G 2016 Sci. Rep. 6 19201
[14] Zhang Y, Chen Z, Pirandola S, Wang X, Zhou C, Chu B, Zhao Y, Xu B, Yu S, Guo H 2020 Phys. Rev. Lett. 125 010502
Google Scholar
[15] Grosshans F, Assche G V, Wenger J, Brouri R, Cerf N J, Grangier P 2003 Nature (London) 421 238
Google Scholar
[16] Leverrier A 2015 Phys. Rev. Lett. 114 070501
Google Scholar
[17] Laudenbach F, Pacher C, Fung C H F, Poppe A, Peev M, Schrenk B, Hentschel M, Walther P, Hübel H 2018 Adv. Quantum Technol. 1 1800011
Google Scholar
[18] Leverrier A 2017 Phys. Rev. Lett. 118 200501
Google Scholar
[19] Chen Z, Zhang Y, Wang G, Li Z, Guo H 2018 Phys. Rev. A 98 012314
Google Scholar
[20] Qi B, Evans P G, Grice W P 2018 Phys. Rev. A 97 012317
Google Scholar
[21] Qi B, Gunther H, Evans P G, Williams B P, Camacho R M, Peters N A 2020 Phys. Rev. Appl. 13 054065
Google Scholar
[22] Huang P, Wang T, Chen R, Wang P, Zhou Y, Zeng G 2021 New J. Phys. 23 113028
Google Scholar
[23] Wu X, Wang Y, Guo Y, Zhong H, Huang D 2021 Phys. Rev. A 103 032604
Google Scholar
[24] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829
Google Scholar
[25] Kogias I, Xiang Y, He Q Y, Adesso G 2017 Phys. Rev. A 95 012315
Google Scholar
[26] Schmid C, Trojek P, Bourennane M, Kurtsiefer C, Zukowski M, Weinfurter H 2005 Phys. Rev. Lett. 95 230505
Google Scholar
[27] He G P 2007 Phys. Rev. Lett. 98 028901
Google Scholar
[28] Schmid C, Trojek P, Bourennane M, Kurtsiefer C, Zukowski M, Weinfurter H 2007 Phys. Rev. Lett. 98 028902
Google Scholar
[29] He G P, Wang Z D 2010 Quantum Inf. Comput. 10 28
[30] Grice W P, Qi B 2019 Phys. Rev. A 100 022339
Google Scholar
[31] Wu X , Wang Y, Huang D 2020 Phys. Rev. A 101 022301
Google Scholar
[32] Liao Q, Liu H, Zhu L, Guo Y 2021 Phys. Rev. A 103 032410
Google Scholar
[33] Liu W, Wang X, Wang N, Du S, Li Y 2017 Phys. Rev. A 96 042312
Google Scholar
[34] Shen Y, Yang J, Guo H 2009 J. Phys. B: At. Mol. Opt. Phys. 42 235506
Google Scholar
[35] Usenko V C, Filip R 2010 Phys. Rev. A 81 022318
Google Scholar
[36] Jouguet P, Kunz J S, Diamanti E, Leverrier A 2012 Phys. Rev. A 86 032309
Google Scholar
[37] Fossier S, Diamanti E, Debuisschert T, Tualle-Brouri R, Grangier P 2009 J. Phys. B: At. Mol. Opt. Phys. 42 114014
Google Scholar
[38] Diamanti E, Leverrier A 2015 Entropy 17 6072
Google Scholar
[39] Lodewyck J, Bloch M, García-Patrón R, Fossier S, Karpov E, Diamanti E, Debuisschert T, Cerf N J, Tualle-Brouri R, McLaughlin S W, Grangier P 2007 Phys. Rev. A 76 042305
Google Scholar
[40] Huang P, He G Q, Zeng G H 2013 Int. J. Theor. Phys. 52 1572
Google Scholar
[41] Huang D, Huang P, Wang T, Li H, Zhou Y, Zeng G 2016 Phys. Rev. A 94 032305
Google Scholar
[42] Zhang H, Fang J, He G 2012 Phys. Rev. A 86 022338
Google Scholar
[43] Pirandola S, Laurenza R, Ottaviani C, Banchi L 2017 Nat. Commun. 8 15043
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2665
- PDF Downloads: 69
- Cited By: 0
