-
相比于离散变量量子密钥分发, 连续变量量子密钥分发虽然具备更高的安全码率等优势, 但是在安全传输距离上却略有不足. 尽管量子催化的运用对高斯调制连续变量量子密钥分发协议的性能, 尤其在安全传输距离方面有着显著的提升, 然而能否用来改善离散调制协议的性能却仍然未知. 鉴于上述分析, 本文提出了一种基于量子催化的离散调制协议的方案, 试图在安全密钥率、安全传输距离和最大可容忍过噪声方面进一步提升协议性能. 研究结果表明, 在相同参数下, 当优化量子催化引入的透射率T, 相比于原始四态调制协议, 所提方案能够有效地提升量子密钥分发的性能. 特别是, 对于可容忍过噪声为0.002, 量子催化可将安全通信距离突破300 km, 密钥率为 10–8 bits/pulse, 而过大的可容忍噪声会抑制量子催化对协议性能的改善效果. 此外, 为了彰显量子催化的优势, 本文给出了点对点量子通信的最终极限Pirandola-Laurenza-Ottaviani-Banchi边界, 仿真结果表明, 虽然原始方案与所提方案都未能突破这种边界, 但是相比于前者, 后者能够在远距离通信上逼近于这种边界, 这为实现全球量子安全通信的最终目标提供理论依据.Compared with discrete variable quantum key distribution (DVQKD), continuous variable (CV) QKD has high security bit rate and other advantages, which, however, are slightly insufficient in secure transmission distance. In addition, the application of quantum catalysis has significantly improved the performance of Gaussian modulated (GM) CVQKD, especially in secure transmission distance. Recently, the application of quantum catalysis has significantly improved the performance of GM-CVQKD. However, whether it can be used to improve the performance of discrete modulated (DM) CVQKD protocol is still ambiguous. Therefore, a scheme of DM CVQKD protocol based on quantum catalysis is proposed in this paper to further improve the performance of the proposed protocol in terms of secure key rate, secure transmission distance and maximum tolerable noise. Our results show that under the same parameters, when the transmittance T introduced by quantum catalysis is optimized, the proposed scheme can effectively further improve the performance of QKD system compared with the original four-state modulation CVQKD scheme. In particular, when the tolerable excess noise is 0.002, the use of quantum catalysis can break the safe communication distance of 300 km with a key rate of 10–8 bits/pulse. However, if this noise is too large, the improvement in the effect of quantum catalysis on protocol performance will be restrained. In addition, in order to highlight the advantages of the use of quantum catalysis, the ultimate limit PLOB (Pirandola-Laurenza-Ottaviani-Banchi) bound of point-to-point quantum communication is given in this paper. The simulation results indicate that although neither the original scheme nor the proposed scheme can break the bound, compared with the former, the latter can be close to the boundary in long-distance transmission. These results provide theoretical basis for achieving the ultimate goal of global quantum security communication.
[1] 李剑, 陈彦桦, 潘泽世, 孙风琪, 李娜, 黎蕾蕾 2016 3 030302
Google Scholar
Li J, Chen Y H, Pan Z S, Sun F Q, Li N, Li L L 2016 Acta Phys. Sin. 3 030302
Google Scholar
[2] 苗二龙, 莫小范, 桂有珍, 韩正甫, 郭光灿 2004 53 2123
Google Scholar
Miao E L, Mo X F, Gui Y Z, Han Z F, Guo G C 2004 Acta Phys. Sin. 53 2123
Google Scholar
[3] 曹正文, 张爽浩, 冯晓毅, 赵光, 柴庚, 李东伟 2017 66 020301
Google Scholar
Cao Z W, Zhang S H, Peng X Y, Zhao G, Chai G, Li D W 2017 Acta Phys. Sin. 66 020301
Google Scholar
[4] Braunstein S L, Loock P V 2005 Rev. Mod. Phys. 77 513
Google Scholar
[5] Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902
Google Scholar
[6] Silberhorn C, Ralph T C, Lütkenhaus N, Leuchs G 2002 Phys. Rev. Lett. 89 167901
Google Scholar
[7] Lodewyck J, Bloch M, GarciaPatron R, Fossier S, Karpov E, Diamanti E, Debuisschert T, Cerf N J, Tualle-Brouri R, McLaughlin S W, Grangier P 2007 Phys. Rev. A 76 042305
Google Scholar
[8] Hu L Y, Liao Z Y, Zubairy M S 2017 Phys. Rev. A 95 012310
Google Scholar
[9] Hu L Y, Wu J N, Liao Z Y, Zubairy M S 2016 J. Phys. B: At. Mol. Phys. 49 175504
Google Scholar
[10] 张欢, 叶炜, 周维东, 胡利云 2019 聊城大学学报 32 21
Zhang H, Ye W, Zhou W D, Hu L Y 2019 Journal of Liaocheng University 32 1672 (in Chinese)
[11] Leverrier A, Grangier P 2009 Phys. Rev. Lett. 102 180504
Google Scholar
[12] Leverrier A, Grangier P 2011 Phys. Rev. A 83 042312
Google Scholar
[13] Huang P, Fang J, Zeng G H 2014 Phys. Rev. A 89 042330
Google Scholar
[14] Huang P, Huang J Z, Zhang Z S, Zeng G H 2018 Phys. Rev. A 97 042311
Google Scholar
[15] Huang P, He G Q, Fang J, Zeng G H 2013 Phys. Rev. A 87 012317
Google Scholar
[16] Li Z Y, Zhang Y C, Wang X Y, Xu B J, Peng X, Guo H 2016 Phys. Rev. A 93 012310
Google Scholar
[17] Zhao Y J, Zhang Y C, Li Z Y, Yu S, Guo H 2017 Quantum Inf. Process. 16 184
Google Scholar
[18] Ma H X, Huang P, Bai D Y, Wang S Y, Bao W S, Zeng G H 2018 Phys. Rev. A 97 042329
Google Scholar
[19] Liao Q, Guo Y, Huang D, Huang P, Zeng G H 2018 New J. Phys. 20 023015
Google Scholar
[20] Guo Y, Ye W, Zhong H, Liao Q 2019 Phys. Rev. A 99 032327
Google Scholar
[21] Zhou W D, Ye W, Liu C J, Hu L Y, Liu S Q 2018 Laser Phys. Lett. 15 065203
Google Scholar
[22] Lvovsky A I, Mlynek J 2002 Phys. Rev. Lett. 88 250401
Google Scholar
[23] Ye W, Zhong H, Liao Q, Huang D, Hu L Y, Guo Y 2019 Opt. Express 27 17186
Google Scholar
[24] Fiurasek J, Cerf N J 2012 Phys. Rev. A 86 060302(R)
Google Scholar
[25] Pirandola S, Laurenza R, Ottaviani C, Banchi L 2017 Nat. Commun. 8 15043
Google Scholar
[26] Ma H X, Huang P, Bai D Y, Wang T, Wang S Y, Bao W S, Zeng G H 2019 Phys. Rev. A 99 022322
Google Scholar
-
图 1 纠缠型的零光子催化四态调制协议原理图
Fig. 1. Schematic diagram of the entanglement-based (EB) model of the four-state modulation protocol using a zero-photon catalysis
图 2
${Z_4}$ 和${Z_G}$ 随调制方差V的变化Fig. 2. Both
${Z_4}$ and${Z_G}$ as a function of the modulation variance V.
图 3 对于不同的调制方差V下量子催化的成功概率
${P_{\rm{d}}}$ 随透射率T的变化(图中从上往下的虚线分别表示V = 1.2, 1.3, 1.4, 1.5)Fig. 3. Success probability of implementing such a zero-photon catalysis as a function of the transmittance T for several different V. The dashed lines from bottom to top correspond to V = 1.2, 1.3, 1.4, 1.5, respectively.
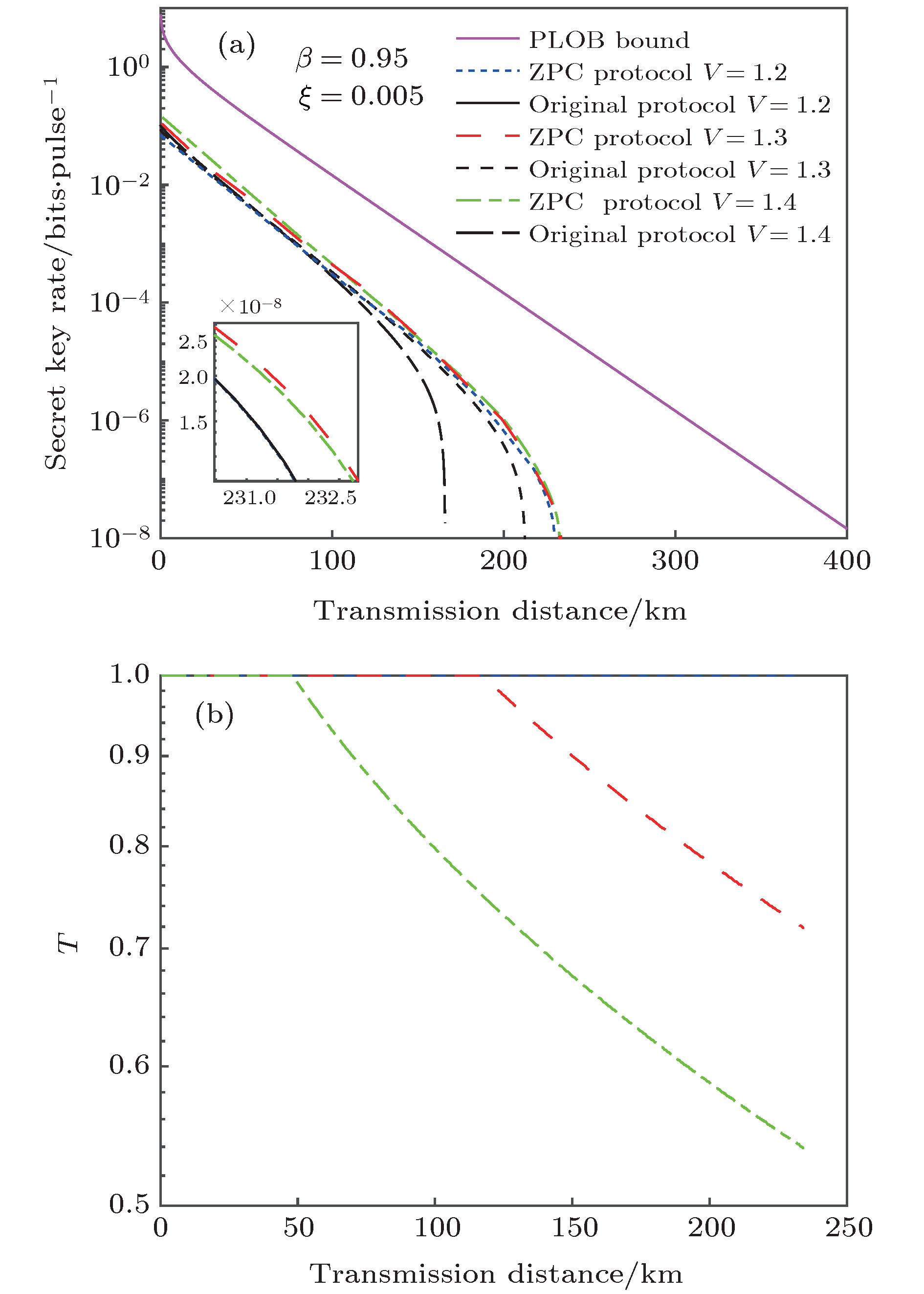
图 4 离散调制量子密钥分发系统的性能比较 (a) 固定参数
$\beta = 0.95, \xi = 0.005$ 下, 当优化透射率T时, 密钥率在不同调制方差随传输距离的变化; (b) 对应 (a) 情况下, 透射率T随传输距离的变化Fig. 4. Comparison of the performances between the original protocol and the ZPC-based four-state modulation protocol: (a) At a fixed
$\beta = 0.95, \xi = 0.005$ , the secret key rate as a function of the transmission distance with different V = 1.2, 1.3, 1.4, when optimized over the transmittance T; (b) the transmittance T as a function of the transmission distance corresponding to panel (a).
图 5 离散调制量子密钥分发系统的性能比较 (a) 固定参数
$\beta = 0.95, V = 1.3$ 下, 当优化透射率T时, 密钥率在不同可容忍过噪声随传输距离的变化; (b) 对应 (a) 情况下, 透射率T随传输距离的变化曲线Fig. 5. Comparison of the performances between the original protocol and the ZPC-based four-state modulation protocol: (a) At a fixed
$\beta = 0.95, V = 1.3$ , the secret key rate as a function of the transmission distance with different$\xi = 0.002, 0.005, 0.008$ , when optimized over the transmittance T; (b) the transmittance T as a function of the transmission distance corresponding to panel (a).
图 6 离散调制量子密钥分发系统的性能比较 (a) 固定参数
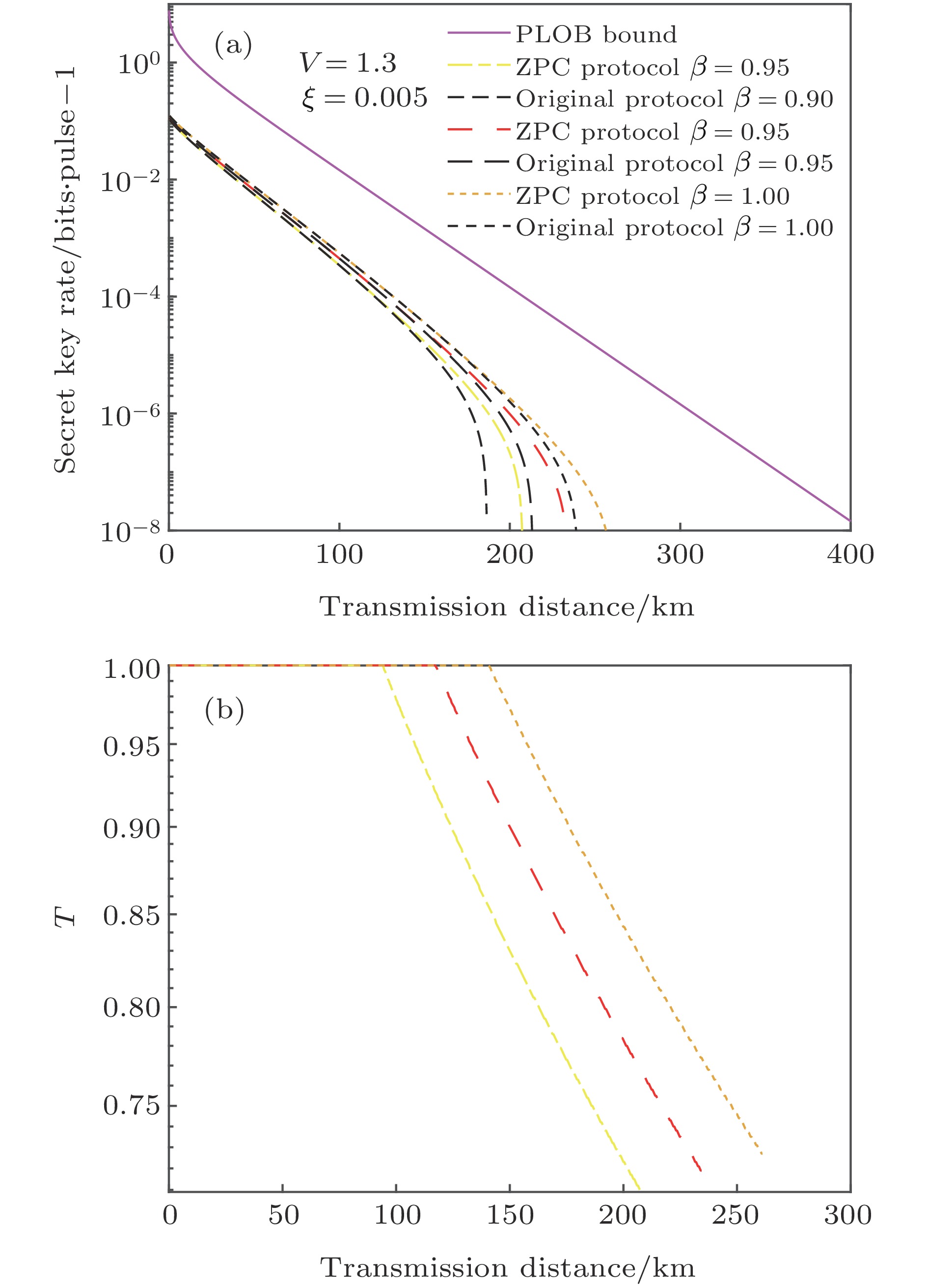
$V = 1.3, \xi = 0.005$ 下, 当优化透射率T时, 密钥率在不同协商效率随传输距离的变化; (b) 对应 (a) 情况下, 透射率T随传输距离的变化曲线Fig. 6. Comparison of the performances between the original protocol and the ZPC-based four-state modulation protocol: (a) At a fixed
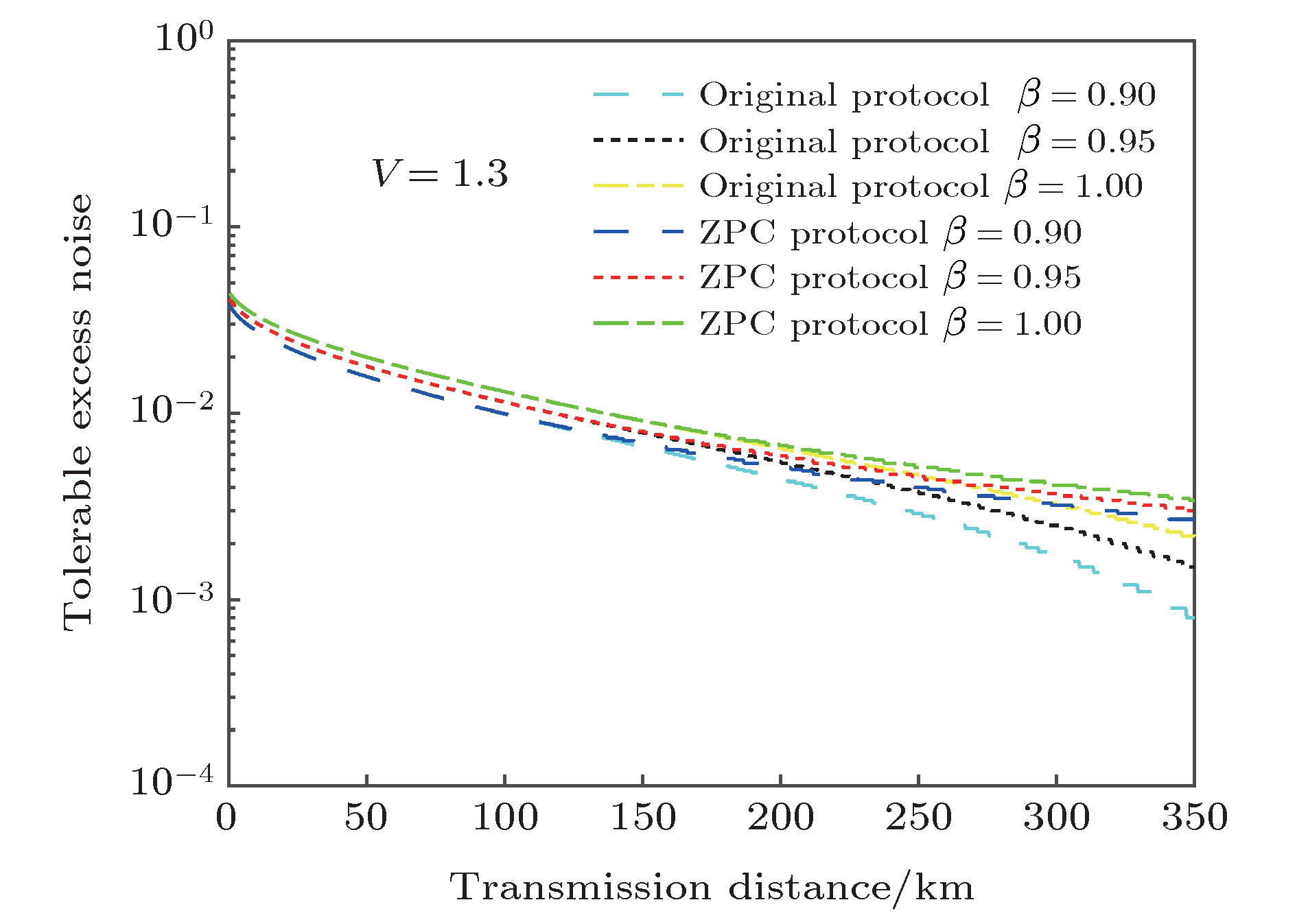
$V = 1.3, \xi = 0.005$ , the secret key rate as a function of the transmission distance with different$\beta = 0.90, 0.95, 1.0$ , when optimized over the transmittance T; (b) the transmittance T as a function of the transmission distance corresponding to panel (a).
图 7 在固定参数
$V = 1.3$ 下, 当优化透射率T时, 可容忍过噪声在不同协商效率随传输距离的变化Fig. 7. At a fixed
$V = 1.3$ , the tolerable excess noise between the original protocol and the ZPC-based four-state modulation protocol as a function of a transmission distance for several different$\beta = 0.90, 0.95, 1.0$ , when optimized over T. -
[1] 李剑, 陈彦桦, 潘泽世, 孙风琪, 李娜, 黎蕾蕾 2016 3 030302
Google Scholar
Li J, Chen Y H, Pan Z S, Sun F Q, Li N, Li L L 2016 Acta Phys. Sin. 3 030302
Google Scholar
[2] 苗二龙, 莫小范, 桂有珍, 韩正甫, 郭光灿 2004 53 2123
Google Scholar
Miao E L, Mo X F, Gui Y Z, Han Z F, Guo G C 2004 Acta Phys. Sin. 53 2123
Google Scholar
[3] 曹正文, 张爽浩, 冯晓毅, 赵光, 柴庚, 李东伟 2017 66 020301
Google Scholar
Cao Z W, Zhang S H, Peng X Y, Zhao G, Chai G, Li D W 2017 Acta Phys. Sin. 66 020301
Google Scholar
[4] Braunstein S L, Loock P V 2005 Rev. Mod. Phys. 77 513
Google Scholar
[5] Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902
Google Scholar
[6] Silberhorn C, Ralph T C, Lütkenhaus N, Leuchs G 2002 Phys. Rev. Lett. 89 167901
Google Scholar
[7] Lodewyck J, Bloch M, GarciaPatron R, Fossier S, Karpov E, Diamanti E, Debuisschert T, Cerf N J, Tualle-Brouri R, McLaughlin S W, Grangier P 2007 Phys. Rev. A 76 042305
Google Scholar
[8] Hu L Y, Liao Z Y, Zubairy M S 2017 Phys. Rev. A 95 012310
Google Scholar
[9] Hu L Y, Wu J N, Liao Z Y, Zubairy M S 2016 J. Phys. B: At. Mol. Phys. 49 175504
Google Scholar
[10] 张欢, 叶炜, 周维东, 胡利云 2019 聊城大学学报 32 21
Zhang H, Ye W, Zhou W D, Hu L Y 2019 Journal of Liaocheng University 32 1672 (in Chinese)
[11] Leverrier A, Grangier P 2009 Phys. Rev. Lett. 102 180504
Google Scholar
[12] Leverrier A, Grangier P 2011 Phys. Rev. A 83 042312
Google Scholar
[13] Huang P, Fang J, Zeng G H 2014 Phys. Rev. A 89 042330
Google Scholar
[14] Huang P, Huang J Z, Zhang Z S, Zeng G H 2018 Phys. Rev. A 97 042311
Google Scholar
[15] Huang P, He G Q, Fang J, Zeng G H 2013 Phys. Rev. A 87 012317
Google Scholar
[16] Li Z Y, Zhang Y C, Wang X Y, Xu B J, Peng X, Guo H 2016 Phys. Rev. A 93 012310
Google Scholar
[17] Zhao Y J, Zhang Y C, Li Z Y, Yu S, Guo H 2017 Quantum Inf. Process. 16 184
Google Scholar
[18] Ma H X, Huang P, Bai D Y, Wang S Y, Bao W S, Zeng G H 2018 Phys. Rev. A 97 042329
Google Scholar
[19] Liao Q, Guo Y, Huang D, Huang P, Zeng G H 2018 New J. Phys. 20 023015
Google Scholar
[20] Guo Y, Ye W, Zhong H, Liao Q 2019 Phys. Rev. A 99 032327
Google Scholar
[21] Zhou W D, Ye W, Liu C J, Hu L Y, Liu S Q 2018 Laser Phys. Lett. 15 065203
Google Scholar
[22] Lvovsky A I, Mlynek J 2002 Phys. Rev. Lett. 88 250401
Google Scholar
[23] Ye W, Zhong H, Liao Q, Huang D, Hu L Y, Guo Y 2019 Opt. Express 27 17186
Google Scholar
[24] Fiurasek J, Cerf N J 2012 Phys. Rev. A 86 060302(R)
Google Scholar
[25] Pirandola S, Laurenza R, Ottaviani C, Banchi L 2017 Nat. Commun. 8 15043
Google Scholar
[26] Ma H X, Huang P, Bai D Y, Wang T, Wang S Y, Bao W S, Zeng G H 2019 Phys. Rev. A 99 022322
Google Scholar
下载:
计量
- 文章访问数: 8515
- PDF下载量: 180
- 被引次数: 0
