-
In tokamak experiments, various magnetohydrodynamic (MHD) instabilities usually co-exist and interact with fast particles. It can cause the fast particles to significantly transport and lose, which results in damaging the first wall and quenching discharge in tokamak. Therefore, the understanding of the physical mechanism of fast particle transport caused by MHD instabilities is crucial and this physical problem needs solving urgently for the steady-state long pulse operation of future reactor-graded devices. According to the phenomenon of synergy between non-resonant internal kink mode and tearing mode, observed experimentally on NSTX, a spherical tokamak device, we utilize the global nonlinear hybrid-kinetic simulation code M3D-K to study and compare the characteristics of loss, transport and redistribution of fast particles in the two cases: 1) the synergy between the non-resonant internal kink mode and tearing mode and 2) only non-resonant internal kink modes. The physical mechanisms of transport, loss, and redistribution of fast particles caused by such synergy are studied, respectively. The results show that the synergy between the non-resonant internal kink mode and the tearing mode can significantly enhance the loss and transport of fast particles. The main reason is that such a synergy can provide a radial channel for fast particles to migrate from the plasma core to the plasma boundary accompanied with the total stochasticity of the magnetic topology. These results can help understand the physical mechanism of the transport and loss of fast particles caused by the synergy of low-frequency MHD instabilities in future fusion reactors, and provide some new ideas for finding strategies to control and mitigate the loss and transport level of fast particles in future fusion reactors.
-
Keywords:
- tokamak /
- tearing mode /
- non-resonant internal kink mode /
- synergy /
- fast-particle transport
[1] Heidbrink W W, White R B 2020 Phys. Plasmas 27 030901
Google Scholar
[2] Chen W, Yu L M, Xu M, Ji X Q, Shi Z B, He X X, Li Z J, Li Y G, Wang T B, Jiang M, Gong S B, Wen J, Shi P W, Yang Z C, Fang K R, Li J, Wei L, Zhong W L, Sun A P, Cao J Y, Bai X Y, Li J Q, Ding X T, Dong J Q, Yang Q W, Liu Y, Yan L W, Wang Z X, Duan X R 2022 Fundam. Res. 2 667
Google Scholar
[3] Yu L M, Chen W, Jiang M, Shi Z B, Ji X Q, Ding X T, Li Y G, Ma R R, Shi P W, Song S D, Yuan B S, Zhou Y, Ma R, Song X M, Dong J Q, Xu M, Liu Y, Yan L W, Yang Q W, Xu Y H, Duan X R, HL-2A Team 2017 Nucl. Fusion 57 036023
Google Scholar
[4] Zhu X L, Wang F, Chen W, Wang Z X 2022 Plasma Sci. Technol. 24 025102
Google Scholar
[5] Li E Z, Igochine V, Dumbrajs O, Xu L, Chen K, Shi T, Hu L 2014 Plasma Phys. Control. Fusion 56 125016
Google Scholar
[6] Chen W, Zhu X L, Wang F, Jiang M, Ji X Q, Qiu Z Y, Shi Z B, Yu D L, Li Y G, Yu L M, Shi P W, Ding X T, Xu M, Wang Z X 2019 Nucl. Fusion 59 096037
Google Scholar
[7] Wang Z X, Tang W K, Wei L 2022 Plasma Sci. Technol. 24 033001
Google Scholar
[8] Yu L M, Chen W, Shi Z B, Wang T B, Ding X T, Ji X Q, Ma R R, Shi P W, Bai X Y, Li J X, Yuan B S, Li Y G, Yang Z C, Zhang Y P, Ma R, Song X M, Lu B, Dong J Q, Zhong W L, Liu Y, Yan L W, Yang Q W, Xu M 2021 Nucl. Fusion 61 026019
Google Scholar
[9] Chen W, Shi Z B, Qiu Z Y, Yu L M, Shi P W, Jiang M, Ji X Q, Li Y G, He X X, Fang K R, Zou Y P, Ma R R, Zhu X L, Zhong W L, Ding X T, Yang Q W, Wang Z X, Li J Q, Xu M, Duan X R 2020 Nucl. Fusion 60 094003
Google Scholar
[10] Liu D, Heidbrink W W, Podesta M, Ren Z Z, Bardoczi L, Fredrickson E D, Fu G Y, Petty C C, Thome K E, Turco F, Van Zeeland M A 2020 Nucl. Fusion 60 112009
Google Scholar
[11] Chen W, Wang Z X 2020 Chin. Phys. Lett 37 125001
Google Scholar
[12] Shi P W, Chen W, Duan X R 2021 Chin. Phys. Lett 38 035202
Google Scholar
[13] Chen W, Yu L M, Shi P W, Ma R, Ji X Q, Jiang M, Zhu X L, Shi Z B, Yu D L, Yuan B S, Li Y G, Yang Z C, Cao J Y, Song S D, Zhong W L, He H D, Dong J Q, Ding X T, Yan L W, Liu Y, Yang Q W, Xu M, Duan X R 2018 Nucl. Fusion 58 014001
Google Scholar
[14] Breslau J A, Chance M S, Chen J, Fu G Y, Gerhartdt S, Gorelenkov N, Jardin S C, Manickam J 2011 Nucl. Fusion 51 063027
Google Scholar
[15] Zhu X L, Chen W, Wang F, Wang Z X 2020 Nucl. Fusion 60 046023
Google Scholar
[16] Cai H S, Fu G Y 2012 Phys. Plasmas 19 072506
Google Scholar
[17] Gao B F, Cai H S, Gao X, Wan Y X 2021 Nucl. Fusion 61 116070
Google Scholar
[18] Ferrari H E, Farengo R, Garcia-Martinez, Clauser C F 2023 Plasma Phys. Control. Fusion 65 025001
Google Scholar
[19] Clauser C, Farengo R, Ferrari H 2019 Comput. Phys. Commun. 234 126
Google Scholar
[20] Zhu X L, Yu L M, Chen W, Shi P W, Ge W L, Wang F, Luan Q B, Sun H E, Wang Z X 2023 Nucl. Fusion 63 036014
Google Scholar
[21] Bonofiglo P J, Podesta M, Vallar M, Gorelenkov N N, Kiptily V, White R B, Giroud C, Brezinsek S, JET Contributors 2022 Nucl. Fusion 62 112002
Google Scholar
[22] Yang J, Fredrickson E D, Podesta M, Poli F M 2022 Plasma Phys. Control. Fusion 64 095005
Google Scholar
[23] Yang J, Podesta M, Fredrickson E D 2021 Plasma Phys. Control. Fusion 63 045003
Google Scholar
[24] Podesta M, Gorelenkova M, White R B 2014 Plasma Phys. Control. Fusion 56 055003
Google Scholar
[25] Podesta M, Gorelenkova M, Teplukhina A A, Bonofiglo P J, Dumont R, Keeling D, Poli F M, White R B, Jet Contributors 2022 Nucl. Fusion 62 126047
Google Scholar
[26] Park W, Belova E V, Fu G Y, Tang X Z, Strauss H R, Sugiyama L E 1999 Phys. Plasmas 6 1796
Google Scholar
[27] Zhu X L, Wang F, Wang Z X 2020 Chin. Phys. B 29 025201
Google Scholar
[28] Zhu X L, Chen W, Podesta M, Wang F, Liu D, Wang Z X 2022 Nucl. Fusion 62 016012
Google Scholar
[29] Shi P W, Zhu X L, Liang A S, Chen W, Shi Z B, Wang T B, Yang Z C, Yu L M, Jiang M, He X X, Bai X Y, Ji X Q, Zhong W L, Xu M, Wang Z X, Duan X R 2022 Nucl. Fusion 62 106009
Google Scholar
[30] Shen W, Fu G Y, Sheng Z M, Breslau J A, Wang F 2014 Phys. Plasmas 21 092514
Google Scholar
[31] Wang F, Fu G Y, Breslau J A, Liu J Y 2013 Phys. Plasmas 20 102506
Google Scholar
[32] Wang F, Fu G Y, Shen W 2017 Nucl. Fusion 57 016034
Google Scholar
[33] Duan S Z, Fu G Y, Cai H S, Li D 2022 Nucl. Fusion 62 056002
Google Scholar
[34] Yang Y R, Chen W, Ye M Y, Yuan J B, Xu M 2020 Nucl. Fusion 60 106012
Google Scholar
[35] Ge W L, Wang J L, Wang F, Wang Z X 2021 Nucl. Fusion 61 116037
Google Scholar
[36] Ge W L, Wang Z X, Wang F, Liu Z X 2023 Nucl. Fusion 63 016007
Google Scholar
[37] Mynick H E 1993 Phys. Fluids B 5 1471
Google Scholar
[38] Briguglio S, Wang X, Zonca F, Vlad G, Fogaccia G, Di Troia C, Fusco V 2014 Phys. Plasmas 21 112301
Google Scholar
[39] Zhang H W, Ma Z W, Zhu J, Zhang W, Oiu Z Y 2022 Nucl. Fusion 62 026047
Google Scholar
[40] Zhu J, Ma Z W, Wang S, Zhang W 2018 Nucl. Fusion 58 046019
Google Scholar
[41] Cai H S, Li D 2022 Natl. Sci. Rev. 9 nwac019
Google Scholar
-
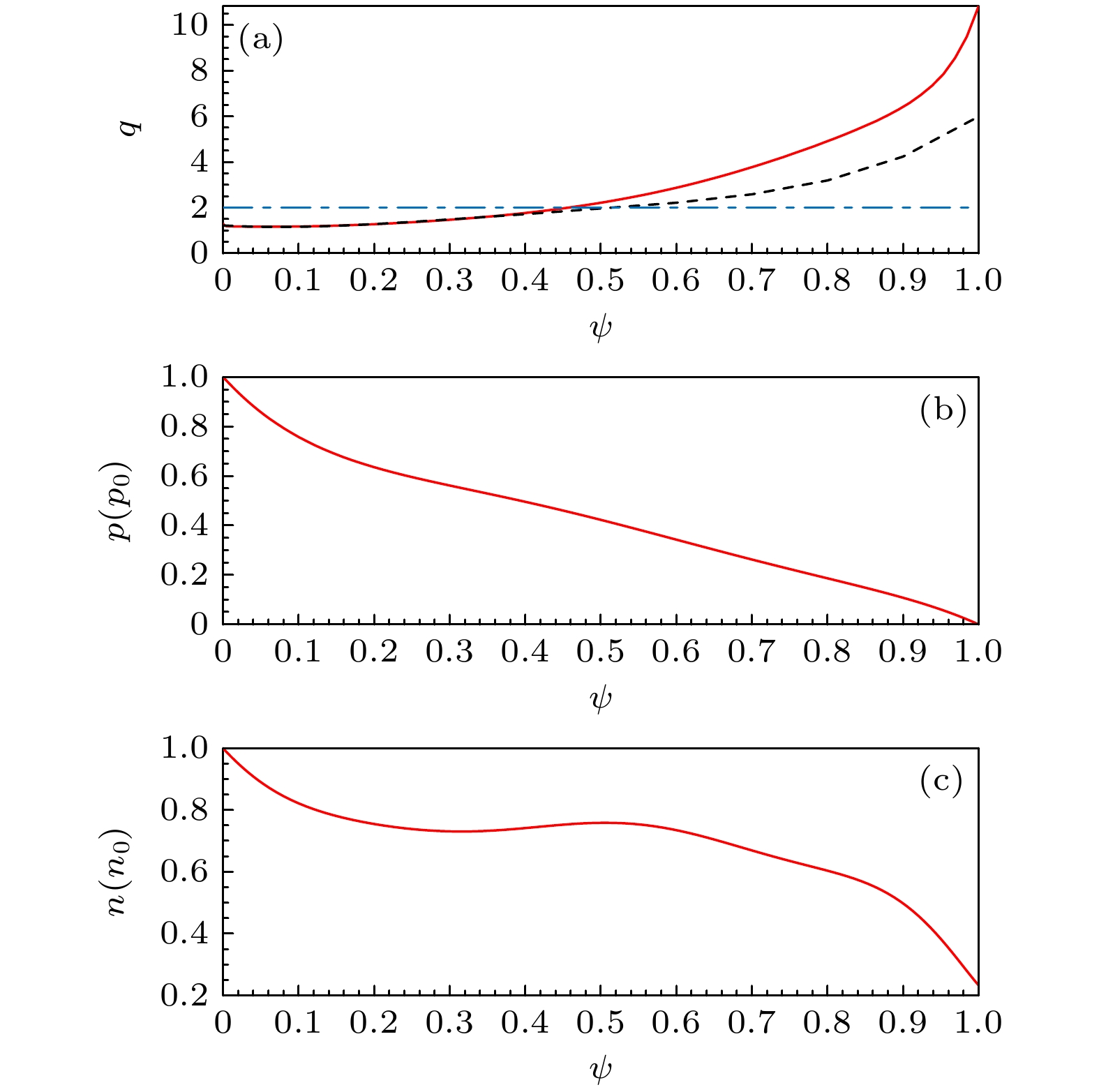
图 1 模拟中采用的平衡剖面—NSTX上 134020 炮
$ t= $ $ 0.64\, \mathrm{s} $ 的实验剖面 (a)安全因子剖面 q (红色实线), 对应下文中情况1, 向下平移后的安全因子剖面 q (黑色虚线), 对应下文中情况2; (b)总压强剖面 p, 包括快离子压强和热压强; (c)等离子体密度剖面 n. 蓝色点划线表示$ q=2 $ Figure 1. Equilibrium profiles used in the simulation, namely the experimental profiles at
$ t = 0.64\, \mathrm{s} $ on NSTX shot 134020: (a) Safety factor profile q denoted by red solid line corresponding to case 1, the down-shifted q profile denoted by black dotted line corresponding to case 2; (b) total pressure profile p including fast ion pressure and thermal plasma pressure; (c) plasma density profile n. Blue dotted line denotes$ q=2 $ .
图 2 (a)
$ t=300\tau_{\rm{A}} $ 时$ m/n=1/1 $ 非共振内扭曲模和$ m/n=2/1 $ 撕裂模存在协同作用情况时的模结构U, 图中从内向外的红色圆圈分别表示$ q=1.24 $ 和$ q=2 $ 两个共振面; (b) 扰动磁场在环向角$ \phi=0 $ 位置处的庞加莱图($t=300\tau_{\rm{A}} $ ); (c)$ t=750\tau_{\rm{A}} $ 时$ m/n=1/1 $ 非共振内扭曲模和$ m/n=2/1 $ 撕裂模存在协同作用情况时的模结构UFigure 2. (a) Mode structure U of coupled
$ m/n=1/1 $ non-resonant kink mode and$ m/n=2/1 $ tearing mode at$ t=300\tau_{\rm{A}} $ , the two red circles from inner to outer respectively denotes$ q=1.24 $ and$ q=2 $ resonant surfaces; (b) the Poincare plot for the perturbed magnetic field line at toroidal angle$ \phi=0 $ ($t=300\tau_{\rm{A}} $ ); (c) the mode structure U of coupled$ m/n=1/1 $ non-resonant kink mode and$ m/n=2/1 $ tearing mode at$ t=750\tau_{\rm{A}} $ .
图 3 (a)
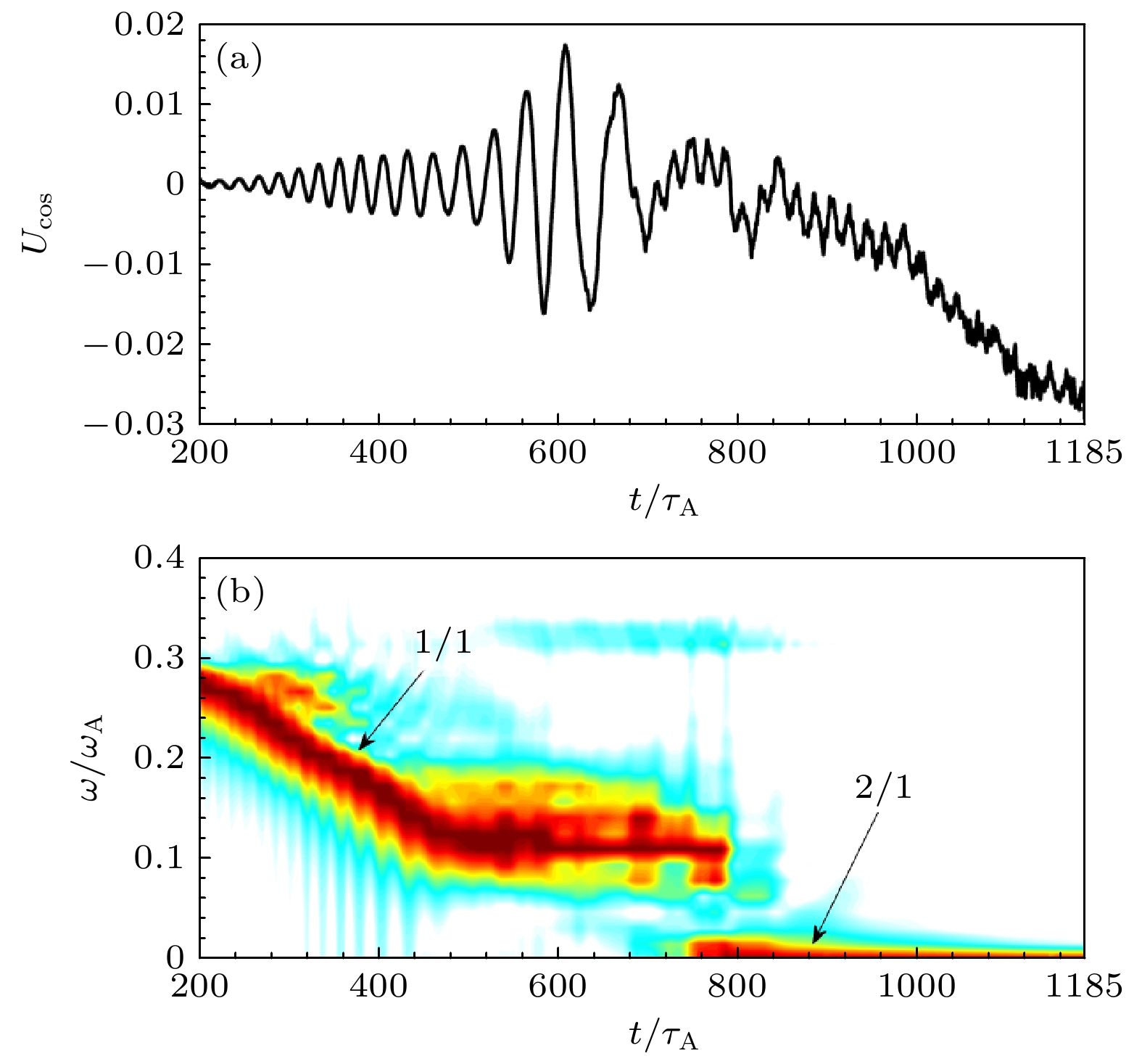
$ m/n=1/1 $ 非共振内扭曲模和$ m/n=2/1 $ 撕裂模存在协同作用情况时模幅度非线性演化; (b)$ m/n= $ $ 1/1 $ 非共振内扭曲模和$ m/n=2/1 $ 撕裂模存在协同相互作用情况的频谱演化Figure 3. (a) Nonlinear evolution of amplitude for coupled
$ m/n=1/1 $ non-resonant kink mode and$ m/n=2/1 $ tearing mode; (b) the evolution of frequency spectrum of coupled$ m/n=1/1 $ non-resonant kink mode and$ m/n= $ $ 2/1 $ tearing mode.
图 4 (a)
$ t=150\tau_{\rm{A}} $ 时$ m/n=1/1 $ 非共振内扭曲模的模结构, 图中的红色圆圈表示$ q=1.24 $ 共振面所在的位置; (b) 扰动磁场在环向角$ \phi=0 $ 位置处的庞加莱图($t=150\tau_{\rm{A}} $ ); (c)$ t=300\tau_{\rm{A}} $ 时$ m/n=1/1 $ 非共振内扭曲模的模结构Figure 4. (a) Mode structure of coupled
$ m/n=1/1 $ non-resonant kink mode at$ t=150\tau_{\rm{A}} $ , the red circle denotes the location of$ q= $ $ 1.24 $ resonance surface; (b) the Poincare plot for the perturbed magnetic field line at toroidal angle$ \phi=0 $ ($t=150\tau_{\rm{A}} $ ); (c) the mode structure of coupled$ m/n=1/1 $ non-resonant kink mode at$ t=300\tau_{\rm{A}} $ .
图 5 (a)
$ m/n=1/1 $ 非共振内扭曲模幅度$ U_{{\rm{cos}}} $ 非线性演化; (b)$ m/n=1/1 $ 非共振内扭曲模的频谱演化Figure 5. (a) Nonlinear evolution of amplitude for
$ m/n=1/1 $ non-resonant kink mode; (b) the evolution of frequency spectrum of$ m/n=1/1 $ non-resonant kink mode.
图 6
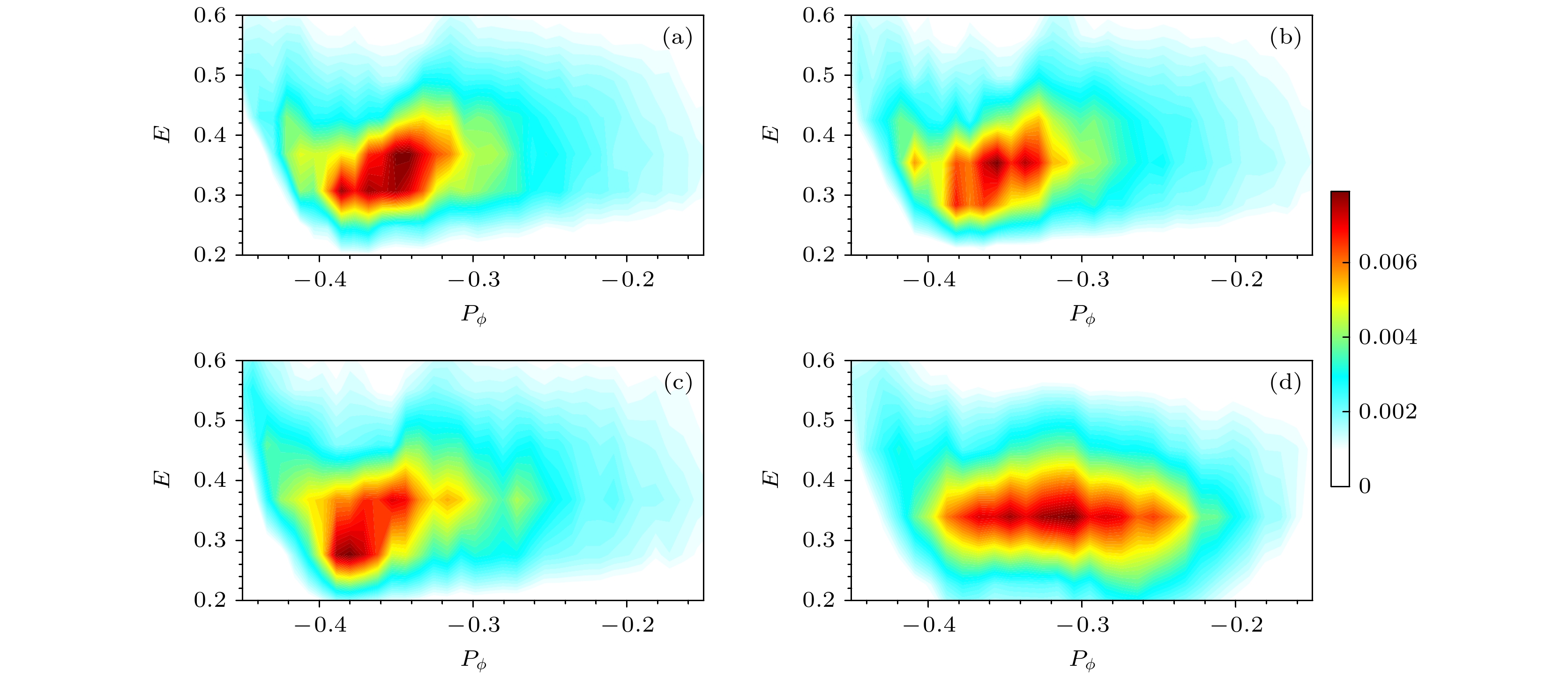
$ m/n=1/1 $ 非共振内扭曲模非线性演化过程中, 在初始时刻(a)$ t=0 $ , 初始饱和时刻(b)$ t=201\tau_{\rm{A}} $ , 非线性饱和前期(c)$ t=300\tau_{\rm{A}} $ , 非线性饱和后期(d)$ t=400\tau_{\rm{A}} $ , 在($ P_\phi, E $ )空间中磁矩$ \mu=0.3343 $ 附近的快粒子分布函数F的演化Figure 6. During the nonlinear evolution of
$ m/n=1/1 $ non-resonant kink mode, the distribution function F around magnetic moment μ = 0.3343 in ($P_\phi, E $ ) space at the initial moment (a)$ t=0 $ , the initial saturation moment (b)$ t=201\tau_{\rm{A}} $ , the late saturation moments (c)$ t=300\tau_{\rm{A}} $ and (d)$ t=400\tau_{\rm{A}} $ .
图 7 耦合的
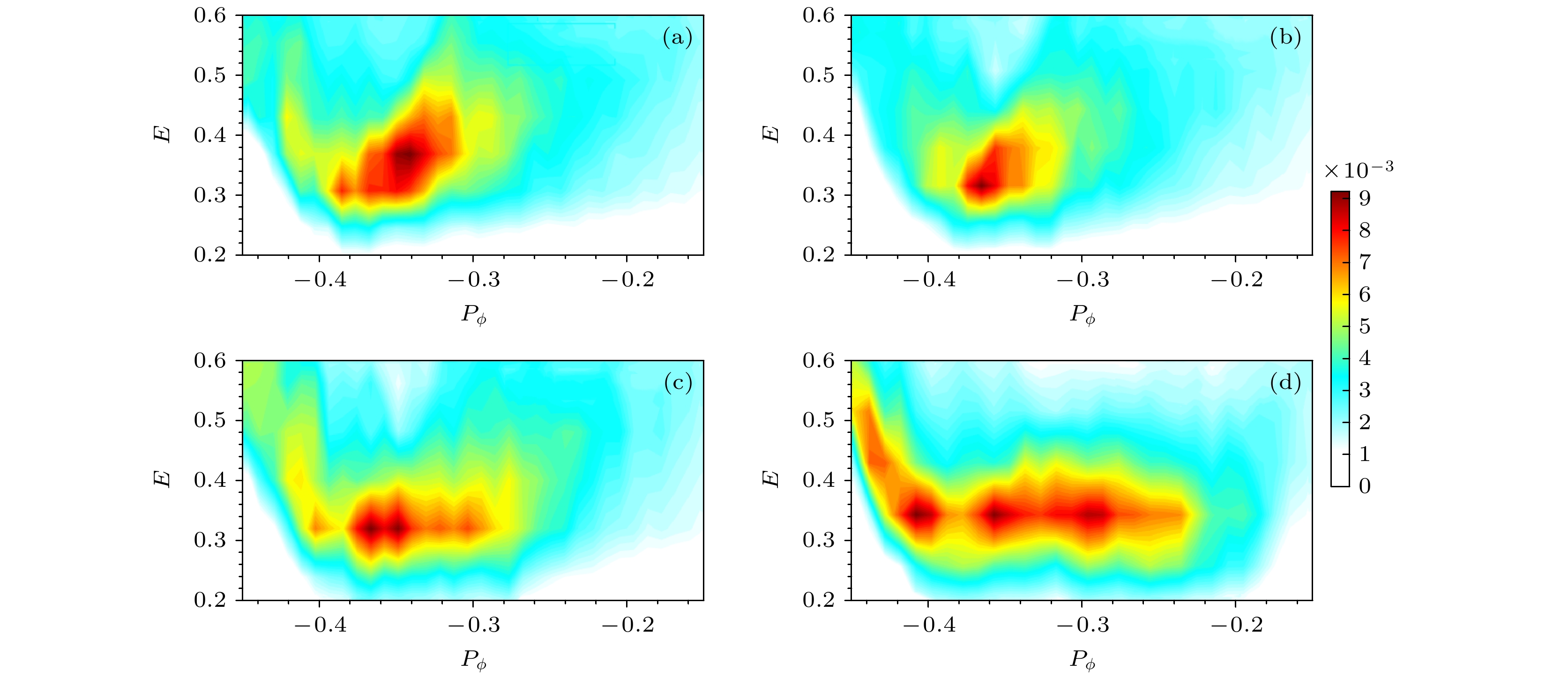
$ m/n=1/1 $ 非共振内扭曲模和$ m/n=2/1 $ 撕裂模非线性演化过程中, 在初始时刻(a)$ t=0 $ , 非线性扫频阶段(b)$ t=400\tau_{\rm{A}} $ , 出现零频分量的阶段(c)$ t=600\tau_{\rm{A}} $ , 非线性饱和后期只有零频分量的阶段(d)$ t=900\tau_{\rm{A}} $ , 在($ P_\phi, E $ ) 空间中磁矩$ \mu=0.3343 $ 附近的快粒子分布函数F的演化Figure 7. During the nonlinear evolution of coupled
$ m/n=1/1 $ non-resonant kink mode and$ m/n=2/1 $ tearing mode, the distribution function F around magnetic moment μ = 0.3343 in ($P_\phi, E $ ) space at the initial moment (a)$ t=0 $ , the initial saturation moment (b)$ t=400\tau_{\rm{A}} $ , the late saturation moments (c)$ t=600\tau_{\rm{A}} $ and (d)$ t=900\tau_{\rm{A}} $ .
图 8 耦合的
$ m/n=1/1 $ 非共振内扭曲模和$ m/n= $ $ 2/1 $ 撕裂模中, 不同模幅度$ A_{{\rm{max}}} $ 与快粒子损失份额$ f_{{\rm{loss}}} $ 的定标关系Figure 8. In the case of coupled
$ m/n=1/1 $ non-resonant kink mode and$ m/n=2/1 $ tearing mode, lost particle fraction$ f_{{\rm{loss}}} $ as a function of the mode amplitude. -
[1] Heidbrink W W, White R B 2020 Phys. Plasmas 27 030901
Google Scholar
[2] Chen W, Yu L M, Xu M, Ji X Q, Shi Z B, He X X, Li Z J, Li Y G, Wang T B, Jiang M, Gong S B, Wen J, Shi P W, Yang Z C, Fang K R, Li J, Wei L, Zhong W L, Sun A P, Cao J Y, Bai X Y, Li J Q, Ding X T, Dong J Q, Yang Q W, Liu Y, Yan L W, Wang Z X, Duan X R 2022 Fundam. Res. 2 667
Google Scholar
[3] Yu L M, Chen W, Jiang M, Shi Z B, Ji X Q, Ding X T, Li Y G, Ma R R, Shi P W, Song S D, Yuan B S, Zhou Y, Ma R, Song X M, Dong J Q, Xu M, Liu Y, Yan L W, Yang Q W, Xu Y H, Duan X R, HL-2A Team 2017 Nucl. Fusion 57 036023
Google Scholar
[4] Zhu X L, Wang F, Chen W, Wang Z X 2022 Plasma Sci. Technol. 24 025102
Google Scholar
[5] Li E Z, Igochine V, Dumbrajs O, Xu L, Chen K, Shi T, Hu L 2014 Plasma Phys. Control. Fusion 56 125016
Google Scholar
[6] Chen W, Zhu X L, Wang F, Jiang M, Ji X Q, Qiu Z Y, Shi Z B, Yu D L, Li Y G, Yu L M, Shi P W, Ding X T, Xu M, Wang Z X 2019 Nucl. Fusion 59 096037
Google Scholar
[7] Wang Z X, Tang W K, Wei L 2022 Plasma Sci. Technol. 24 033001
Google Scholar
[8] Yu L M, Chen W, Shi Z B, Wang T B, Ding X T, Ji X Q, Ma R R, Shi P W, Bai X Y, Li J X, Yuan B S, Li Y G, Yang Z C, Zhang Y P, Ma R, Song X M, Lu B, Dong J Q, Zhong W L, Liu Y, Yan L W, Yang Q W, Xu M 2021 Nucl. Fusion 61 026019
Google Scholar
[9] Chen W, Shi Z B, Qiu Z Y, Yu L M, Shi P W, Jiang M, Ji X Q, Li Y G, He X X, Fang K R, Zou Y P, Ma R R, Zhu X L, Zhong W L, Ding X T, Yang Q W, Wang Z X, Li J Q, Xu M, Duan X R 2020 Nucl. Fusion 60 094003
Google Scholar
[10] Liu D, Heidbrink W W, Podesta M, Ren Z Z, Bardoczi L, Fredrickson E D, Fu G Y, Petty C C, Thome K E, Turco F, Van Zeeland M A 2020 Nucl. Fusion 60 112009
Google Scholar
[11] Chen W, Wang Z X 2020 Chin. Phys. Lett 37 125001
Google Scholar
[12] Shi P W, Chen W, Duan X R 2021 Chin. Phys. Lett 38 035202
Google Scholar
[13] Chen W, Yu L M, Shi P W, Ma R, Ji X Q, Jiang M, Zhu X L, Shi Z B, Yu D L, Yuan B S, Li Y G, Yang Z C, Cao J Y, Song S D, Zhong W L, He H D, Dong J Q, Ding X T, Yan L W, Liu Y, Yang Q W, Xu M, Duan X R 2018 Nucl. Fusion 58 014001
Google Scholar
[14] Breslau J A, Chance M S, Chen J, Fu G Y, Gerhartdt S, Gorelenkov N, Jardin S C, Manickam J 2011 Nucl. Fusion 51 063027
Google Scholar
[15] Zhu X L, Chen W, Wang F, Wang Z X 2020 Nucl. Fusion 60 046023
Google Scholar
[16] Cai H S, Fu G Y 2012 Phys. Plasmas 19 072506
Google Scholar
[17] Gao B F, Cai H S, Gao X, Wan Y X 2021 Nucl. Fusion 61 116070
Google Scholar
[18] Ferrari H E, Farengo R, Garcia-Martinez, Clauser C F 2023 Plasma Phys. Control. Fusion 65 025001
Google Scholar
[19] Clauser C, Farengo R, Ferrari H 2019 Comput. Phys. Commun. 234 126
Google Scholar
[20] Zhu X L, Yu L M, Chen W, Shi P W, Ge W L, Wang F, Luan Q B, Sun H E, Wang Z X 2023 Nucl. Fusion 63 036014
Google Scholar
[21] Bonofiglo P J, Podesta M, Vallar M, Gorelenkov N N, Kiptily V, White R B, Giroud C, Brezinsek S, JET Contributors 2022 Nucl. Fusion 62 112002
Google Scholar
[22] Yang J, Fredrickson E D, Podesta M, Poli F M 2022 Plasma Phys. Control. Fusion 64 095005
Google Scholar
[23] Yang J, Podesta M, Fredrickson E D 2021 Plasma Phys. Control. Fusion 63 045003
Google Scholar
[24] Podesta M, Gorelenkova M, White R B 2014 Plasma Phys. Control. Fusion 56 055003
Google Scholar
[25] Podesta M, Gorelenkova M, Teplukhina A A, Bonofiglo P J, Dumont R, Keeling D, Poli F M, White R B, Jet Contributors 2022 Nucl. Fusion 62 126047
Google Scholar
[26] Park W, Belova E V, Fu G Y, Tang X Z, Strauss H R, Sugiyama L E 1999 Phys. Plasmas 6 1796
Google Scholar
[27] Zhu X L, Wang F, Wang Z X 2020 Chin. Phys. B 29 025201
Google Scholar
[28] Zhu X L, Chen W, Podesta M, Wang F, Liu D, Wang Z X 2022 Nucl. Fusion 62 016012
Google Scholar
[29] Shi P W, Zhu X L, Liang A S, Chen W, Shi Z B, Wang T B, Yang Z C, Yu L M, Jiang M, He X X, Bai X Y, Ji X Q, Zhong W L, Xu M, Wang Z X, Duan X R 2022 Nucl. Fusion 62 106009
Google Scholar
[30] Shen W, Fu G Y, Sheng Z M, Breslau J A, Wang F 2014 Phys. Plasmas 21 092514
Google Scholar
[31] Wang F, Fu G Y, Breslau J A, Liu J Y 2013 Phys. Plasmas 20 102506
Google Scholar
[32] Wang F, Fu G Y, Shen W 2017 Nucl. Fusion 57 016034
Google Scholar
[33] Duan S Z, Fu G Y, Cai H S, Li D 2022 Nucl. Fusion 62 056002
Google Scholar
[34] Yang Y R, Chen W, Ye M Y, Yuan J B, Xu M 2020 Nucl. Fusion 60 106012
Google Scholar
[35] Ge W L, Wang J L, Wang F, Wang Z X 2021 Nucl. Fusion 61 116037
Google Scholar
[36] Ge W L, Wang Z X, Wang F, Liu Z X 2023 Nucl. Fusion 63 016007
Google Scholar
[37] Mynick H E 1993 Phys. Fluids B 5 1471
Google Scholar
[38] Briguglio S, Wang X, Zonca F, Vlad G, Fogaccia G, Di Troia C, Fusco V 2014 Phys. Plasmas 21 112301
Google Scholar
[39] Zhang H W, Ma Z W, Zhu J, Zhang W, Oiu Z Y 2022 Nucl. Fusion 62 026047
Google Scholar
[40] Zhu J, Ma Z W, Wang S, Zhang W 2018 Nucl. Fusion 58 046019
Google Scholar
[41] Cai H S, Li D 2022 Natl. Sci. Rev. 9 nwac019
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2575
- PDF Downloads: 62
- Cited By: 0
