-
湍流非线性作用产生的等离子体流可以通过剪切抑制湍流及其驱动的输运, 从而改善等离子体约束. 湍流可以由局域梯度驱动及远大于其相关长度的径向位置的湍流传播. 采用快速往复朗缪尔探针阵列在中国环流器2号A(HL-2A)托卡马克上观测了电子回旋共振加热 (electron cyclotron resonance heating, ECRH)调制对边缘湍流驱动和传播的影响. 边缘径向电场、湍流和雷诺协强在ECRH期间均增强且伴随着离子-离子碰撞率降低. 分析表明边缘极向流的增强是由于湍流非线性驱动增大和阻尼减弱的共同作用结果. 进一步分析发现ECRH开启后湍流驱动和传播率均增大, 且湍流驱动率大于湍流传播率, 并与湍流强度做比较. 结果表明ECRH期间边缘湍流驱动和传播共同作用导致湍流强度增加, 进而引起湍流雷诺协强增强并驱动更强的边缘等离子体流. 这些结果阐明了ECRH调制期间边缘湍流驱动和传播对边缘等离子体流和湍流的重要影响.
-
关键词:
- 托卡马克 /
- 电子回旋共振加热调制 /
- 边缘流和湍流 /
- 朗缪尔探针
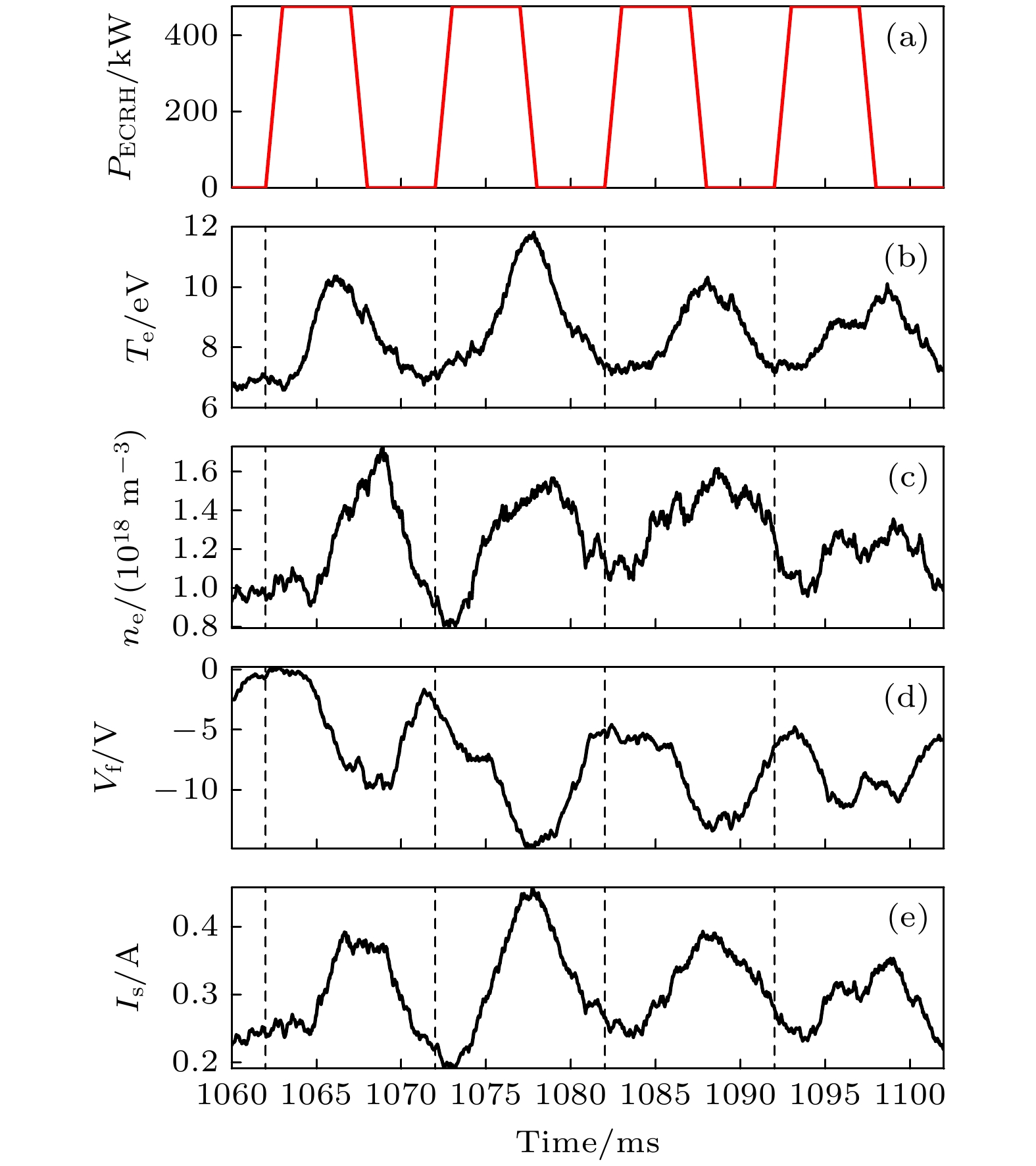
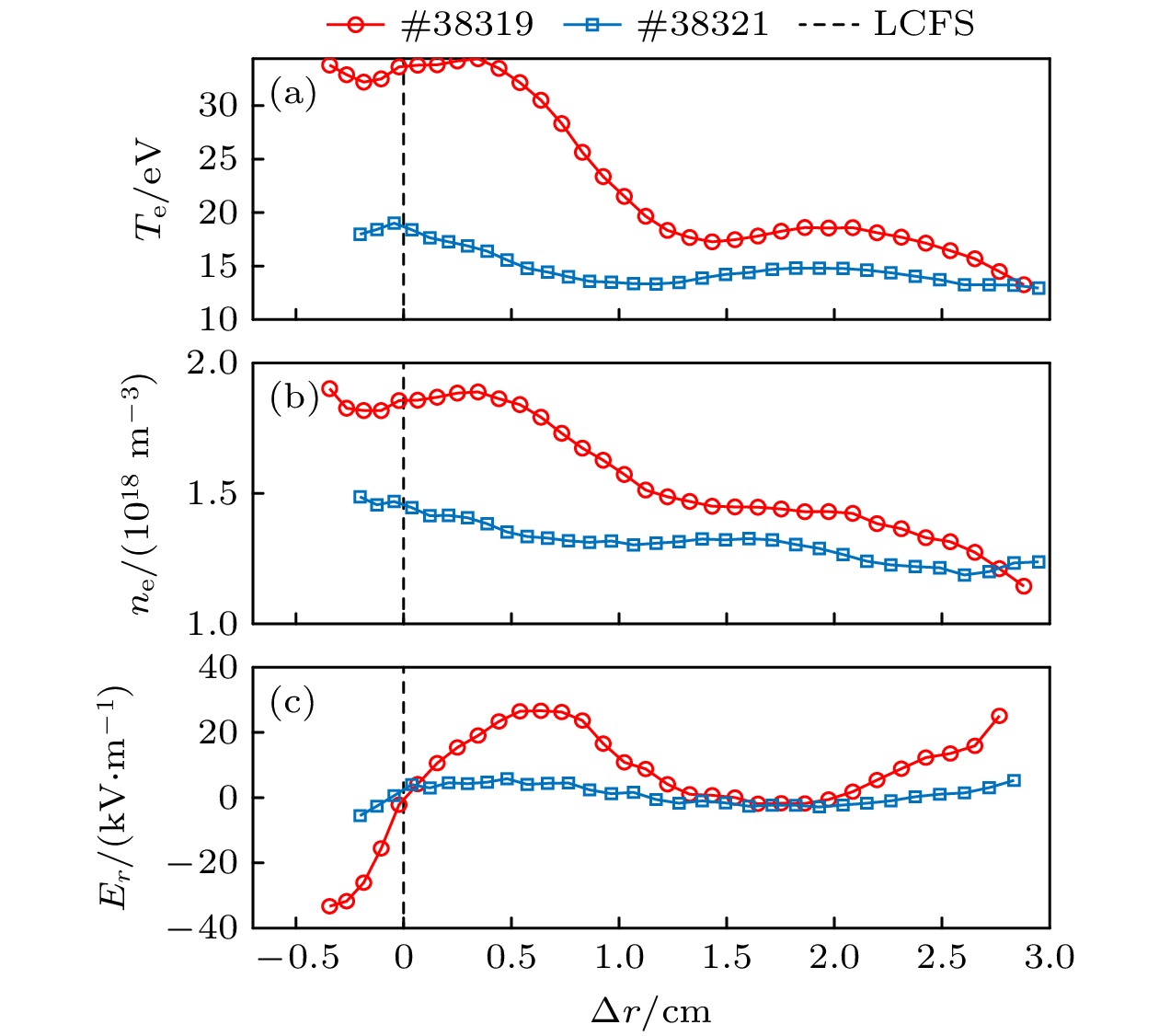
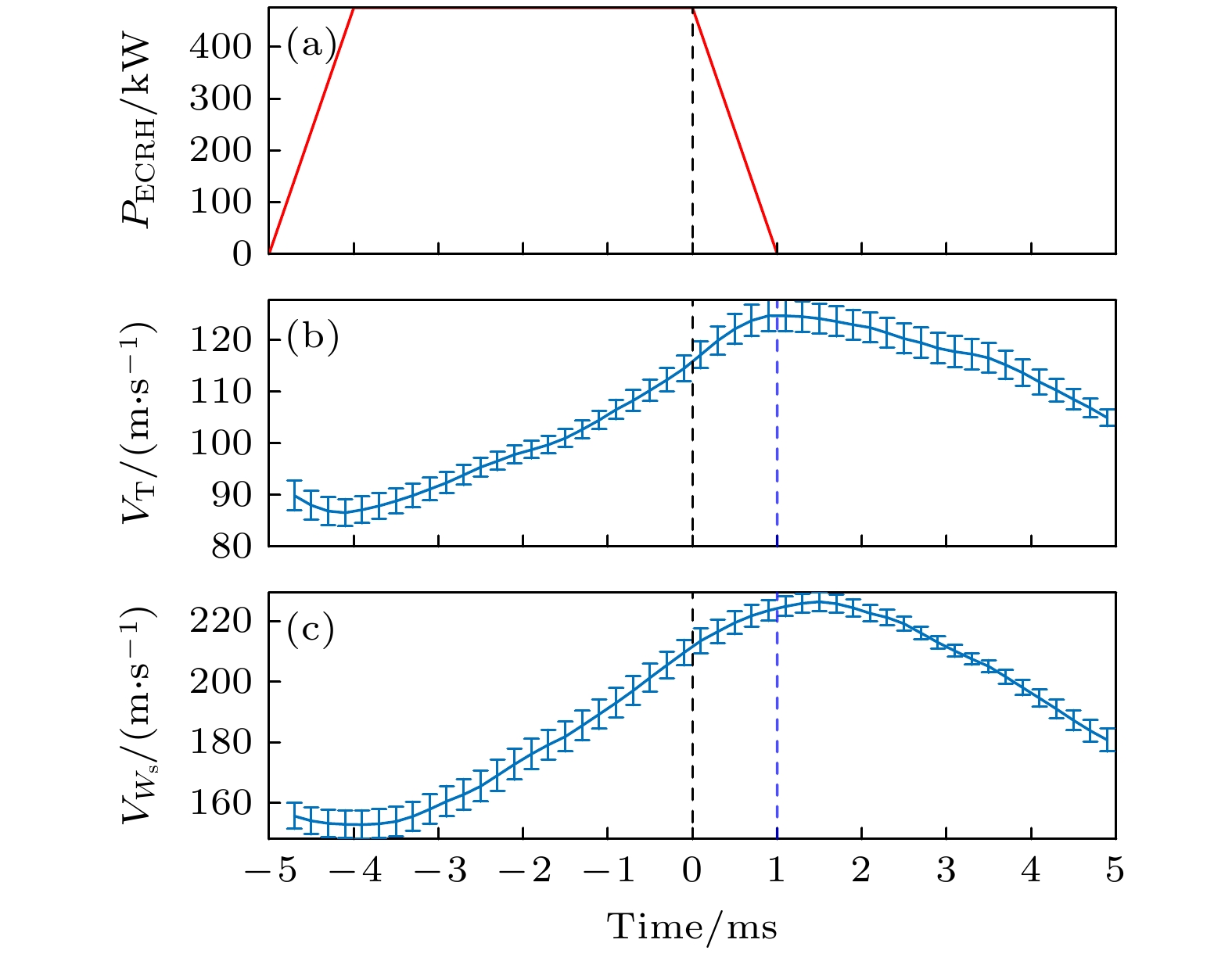
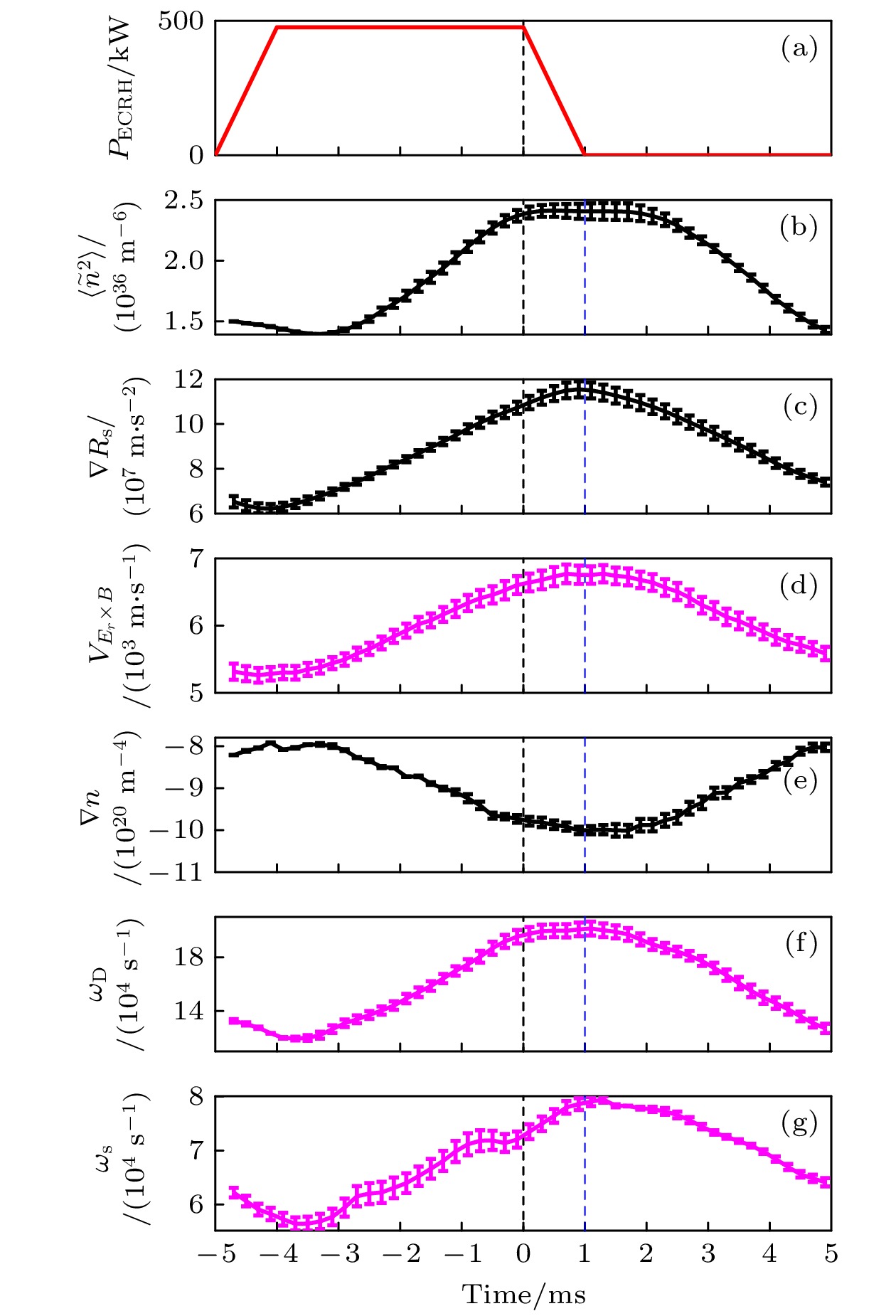
The plasma flow generated by turbulent nonlinear interaction can improve plasma confinement by suppressing turbulence and its driven transport. Turbulence can be driven by local gradients and propagate radially from far beyond its relevant length. Effects of electron cyclotron resonance heating (ECRH) modulation on edge turbulence driving and spreading are observed for the first time in the edge plasma of the HL-2A tokamak. These experiments are performed by a fast reciprocating Langmuir probe array. When ECRH modulation is applied, both the edge temperature and the edge plasma density are higher, and the radial electric field is stronger. The edge radial electric field, turbulence, and Reynolds stresses are all enhanced when the ECRH is applied, while the ion-ion collision rate is reduced. Figures (a)－(g) show the conditional averages of the ECRH power, turbulence intensity, turbulent Reynolds stress gradient, $ {\boldsymbol{E}}_{r}\times \boldsymbol{B} $ poloidal velocity, density gradient, turbulence drive rate and turbulence spreading rate, respectively. With ECRH applied, both the turbulence intensity and the Reynolds stress gradients increase. The maximum turbulence intensity appears at the beginning of the ECRH switch-off while the maximum stress gradient occurs at the end of the ECRH. The evolution of the $ {\boldsymbol{E}}_{r}\times \boldsymbol{B} $ poloidal velocity is very similar to that of the Reynolds stress gradient. This observation suggests that the poloidal flow is the result of the combined effect of turbulence nonlinear driving and damping. The enhancement of Reynolds stress during ECRH modulation mainly depends on the increase of the turbulence intensity, with the increase in radial velocity fluctuation intensity being more significant. The turbulence drive and spreading rates also increase with ECRH. The maximum drive rate appears at the beginning of the ECRH switch-off, while the maximum spreading rate occurs at the end of the ECRH. This analysis indicates that turbulence driving and spreading are enhanced, with the former being dominant. This result suggests that the enhancements of turbulence driving and spreading lead the turbulence and Reynolds stress to increase, and thus producing the stronger edge flows.
-
Keywords:
- tokamak /
- electron cyclotron resonance heating modulation /
- edge flow and turbulence /
- Langmuir probes
-
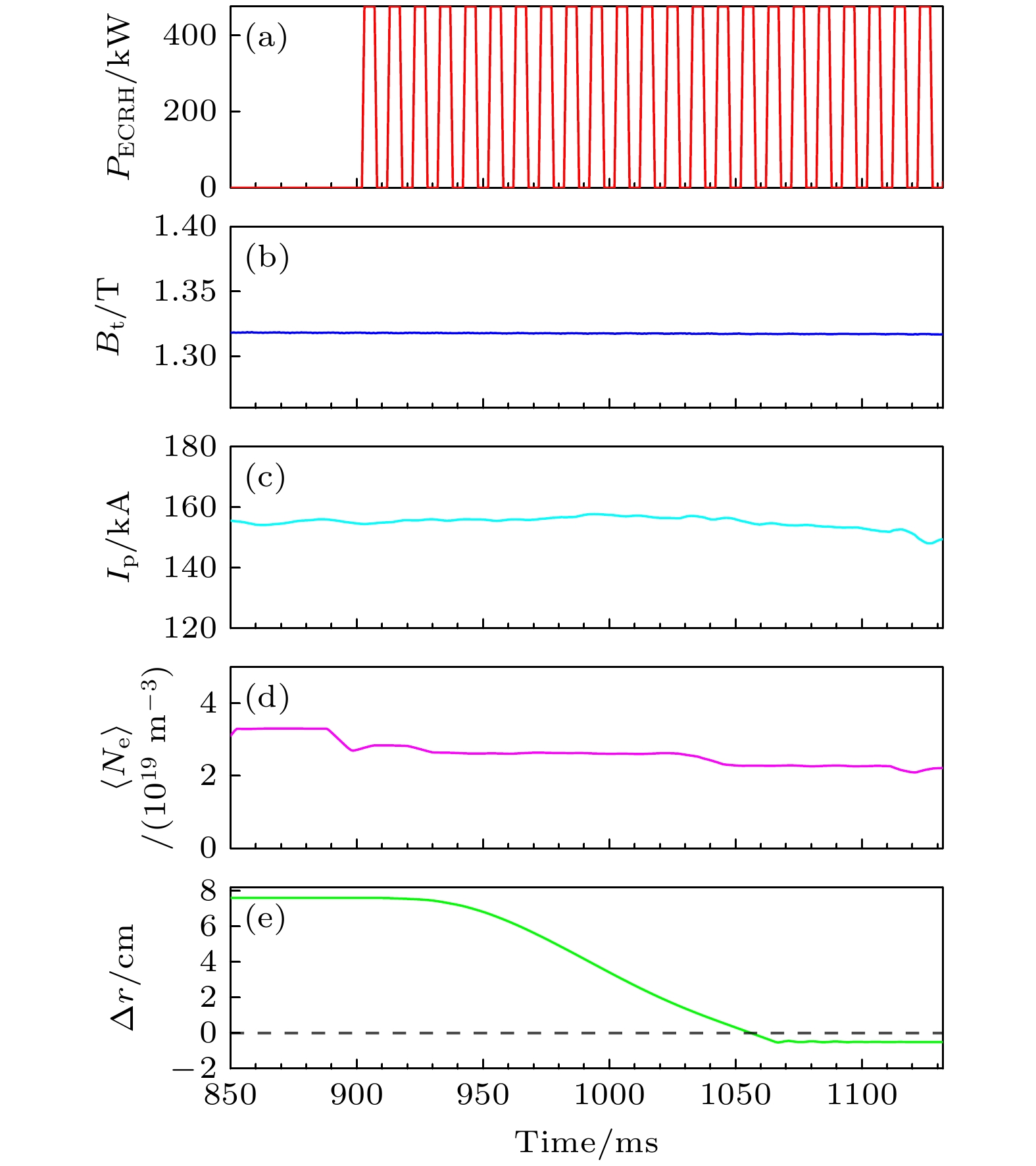
图 2 等离子体参数的时间演化 (a) ECRH功率; (b)环向磁场强度$ {B}_{{\mathrm{t}}}; $ (c)等离子体电流$ {I}_{{\mathrm{p}}}; $ (d)线平均电子密度$ \left\langle{{N}_{{\mathrm{e}}}}\right\rangle; $ (e)探针位移
Fig. 2. Time evolutions of plasma parameters: (a) ECRH power, (b) toroidal magnetic field $ {B}_{{\mathrm{t}}} $, (c) plasma current $ {I}_{{\mathrm{p}}} $, (d) line-averaged electronic density $ \left\langle{{N}_{{\mathrm{e}}}}\right\rangle $; (e) probe displacement.
图 3 边缘等离子体参数的时间演化 (a) ECRH功率; (b)温度; (c)密度; (d)悬浮电位; (e)离子饱和电流
Fig. 3. Time evolutions of edge plasma parameters: (a) ECRH power; (b) temperature; (c) density; (d) floating potential; (e) ion saturation current.
图 4 有无ECRH调制的(a)温度, (b)密度和(c)径向电场的径向分布
Fig. 4. The radial profiles of (a) temperature, (b) density, and (c) radial electric field with and without ECRH modulation.
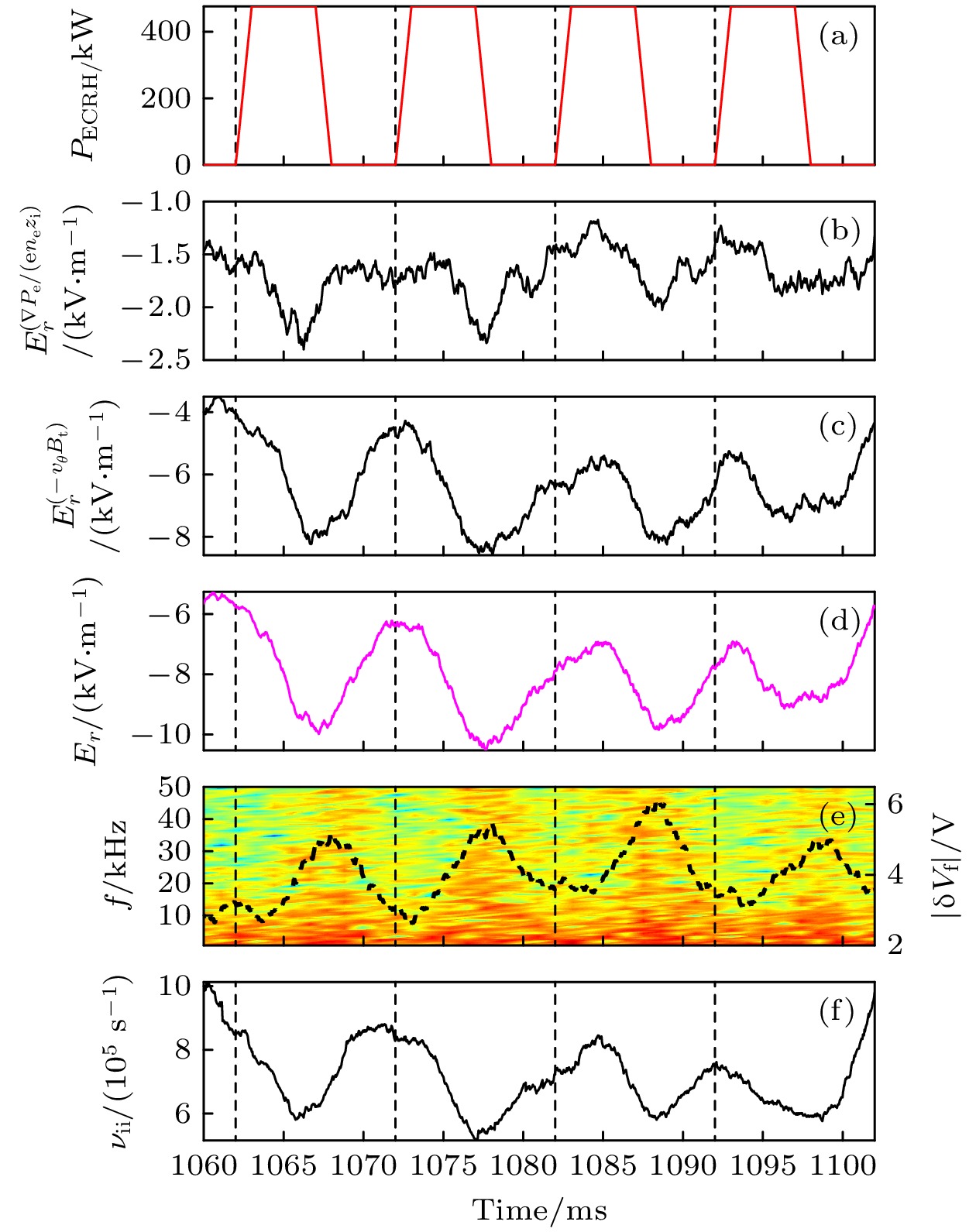
图 5 (a) ECRH功率, (b)压强梯度$ {\nabla P}_{{\mathrm{e}}}/{en}_{{\mathrm{e}}}{Z}_{{\mathrm{i}}} $和(c)极向流$ -{v}_{{\mathrm{\theta }}}{B}_{{\mathrm{t}}} $贡献的径向电场, (d)径向电场$ {E}_{{\mathrm{r}}} $, (e)悬浮电位涨落(虚线)以及其时频图和(f)离子-离子碰撞率的时间演化
Fig. 5. Time evolutions of (a) ECRH power, contributions of (b) pressure gradient $ {\nabla P}_{{\mathrm{e}}}/({en}_{{\mathrm{e}}}{Z}_{{\mathrm{i}}}) $ and (c) poloidal flows ($ -{v}_{{\mathrm{\theta }}}{B}_{{\mathrm{t}}} $) to the radial electric field, (d) radial electric field, (e) floating potential fluctuation (dash line) and its spectrogram and (e) ion-ion collision rate.
图 6 (a) ECRH功率, (b)湍流雷诺协强及其(c)梯度和(d) $ {\boldsymbol{E}}_{r}\times \boldsymbol{B} $极向速度的变化的条件平均
Fig. 6. Conditional averages of (a) ECRH power, (b) Reynolds stress and (c) its gradient, and (d) $ {\boldsymbol{E}}_{r}\times \boldsymbol{B} $ poloidal velocity.
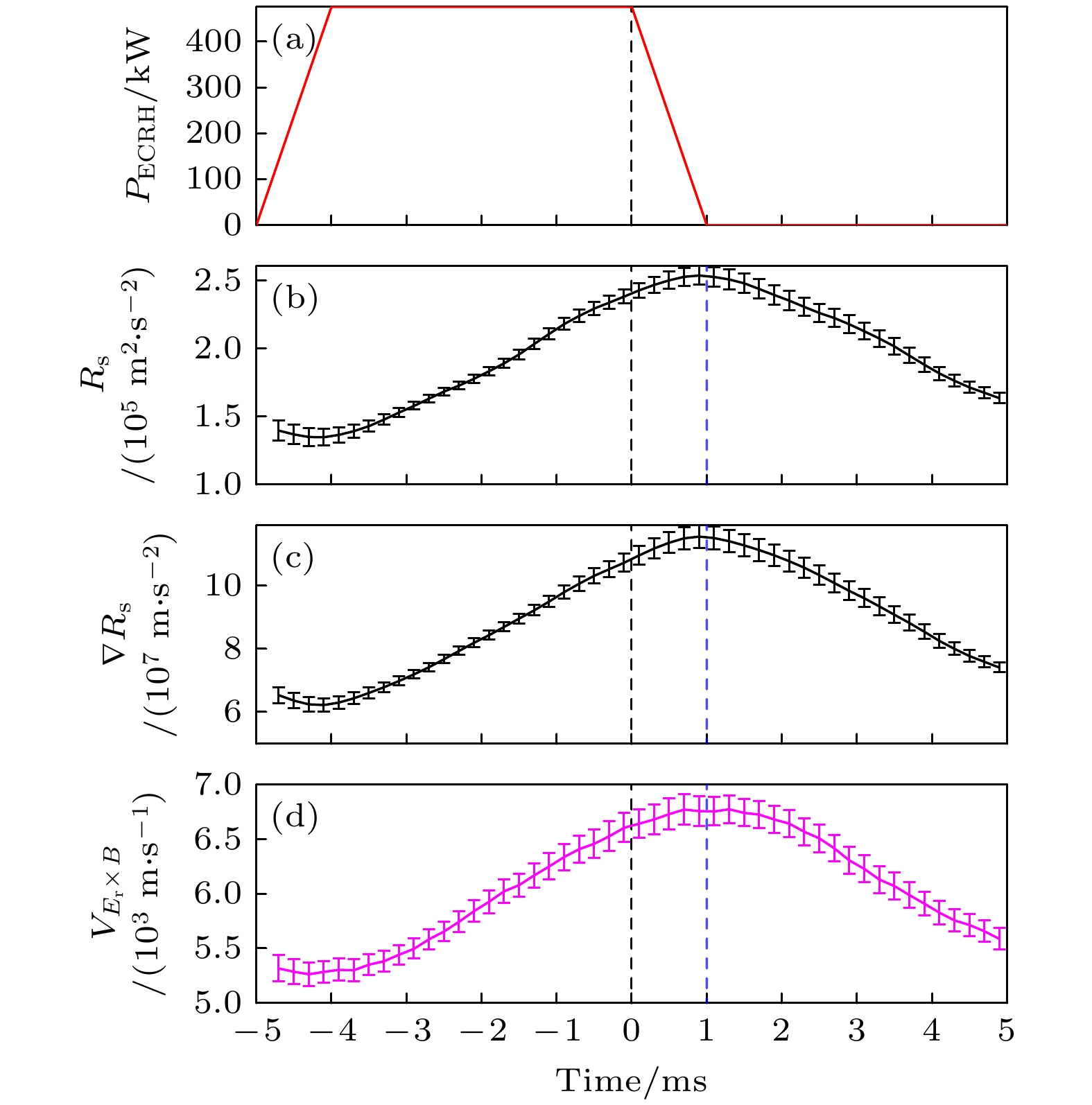
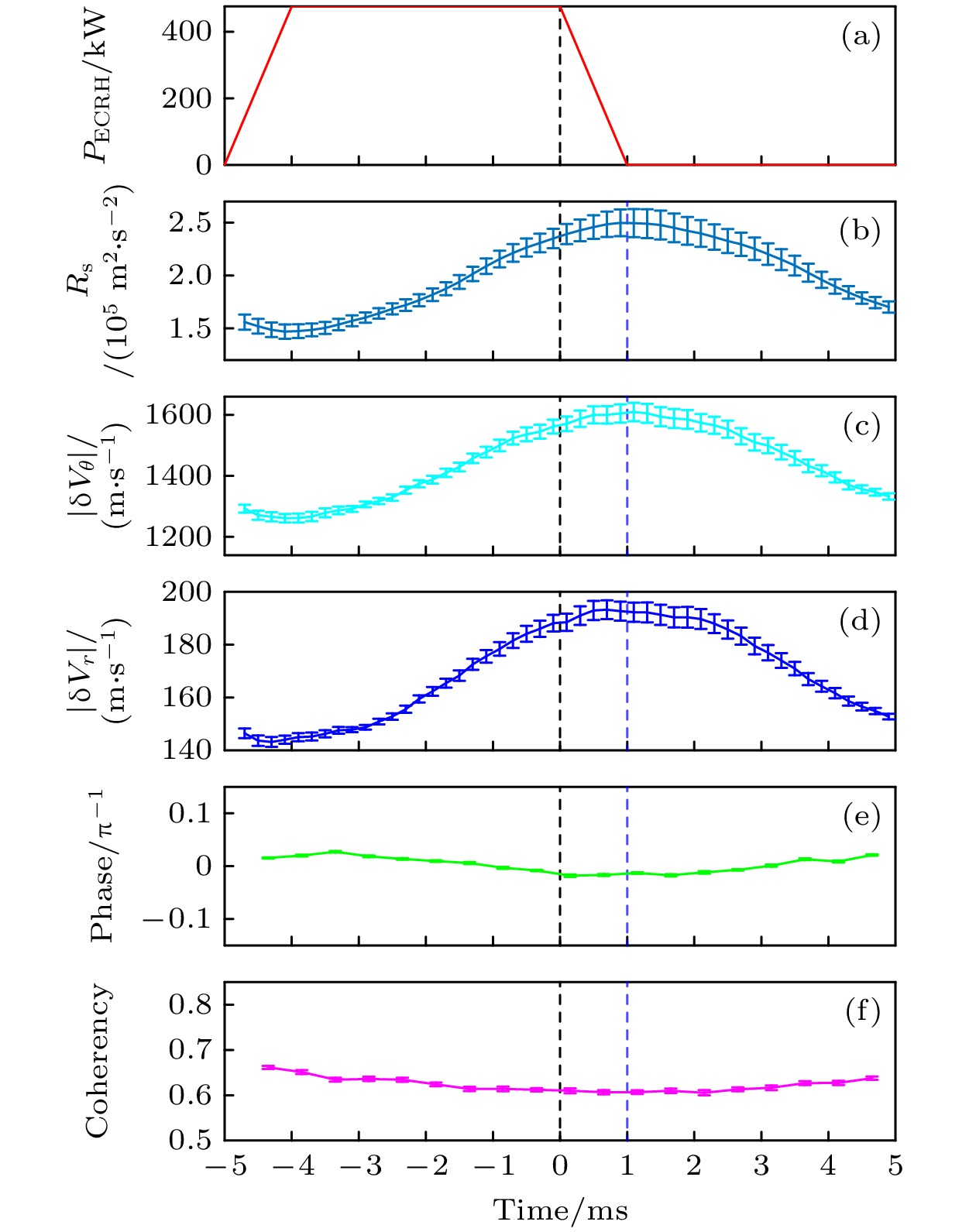
图 7 (a) ECRH功率, (b)雷诺协强(Rs), (c)极向速度涨落, (d)径向速度涨落, 径向和极向速度涨落的(e)相位差, 及其(f)相关系数的条件平均
Fig. 7. Conditional averages of (a) ECRH power, (b) Reynolds stress (Rs) , (c) poloidal velocity fluctuation, (d) radial velocity fluctuation, (e) the phase difference between the radial and poloidal velocity fluctuations, and (f) their coherencies.
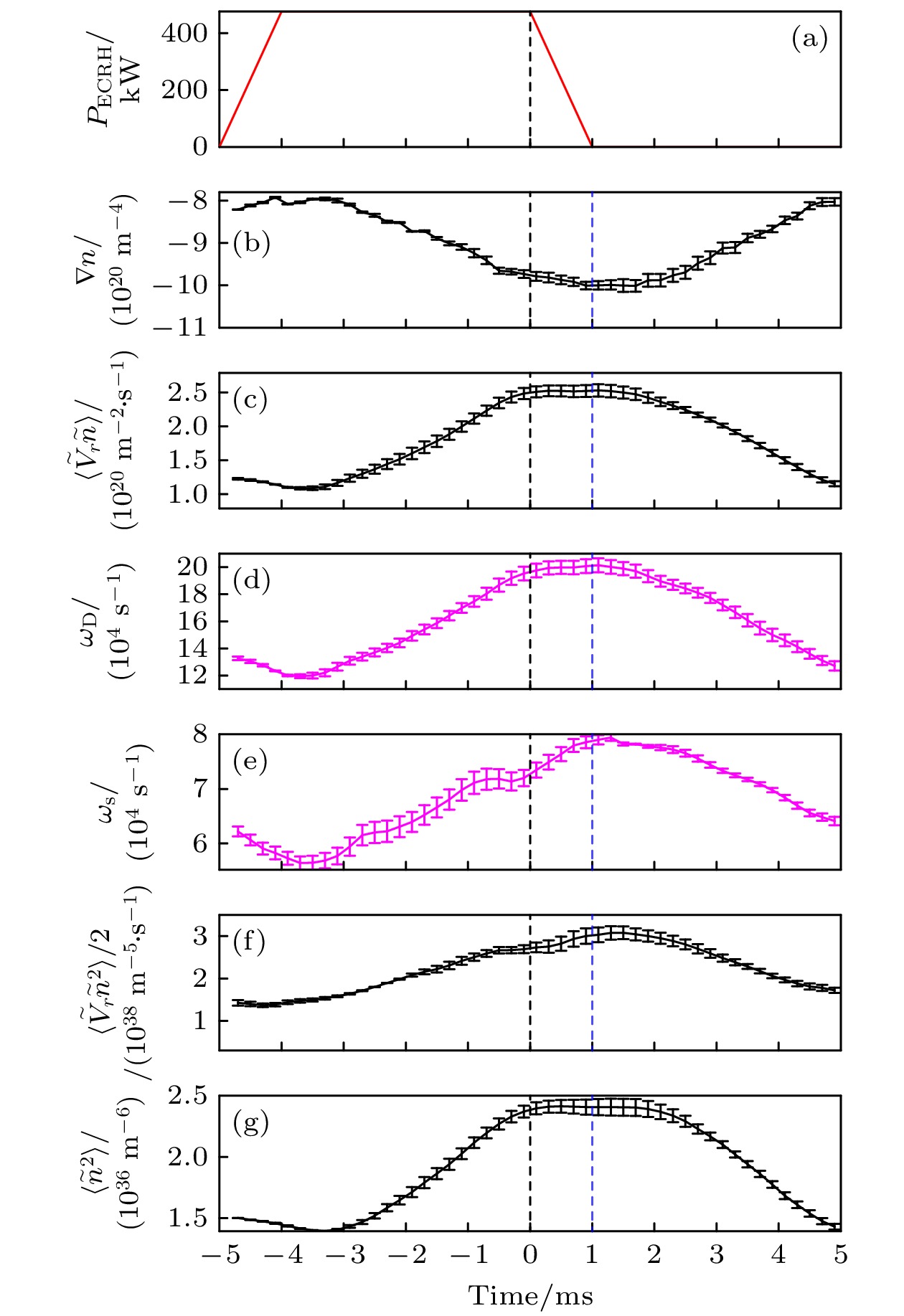
图 8 (a) ECRH功率, (b)密度的梯度, (c)湍流驱动的通量, (d)湍流驱动率($ {\omega }_{{\mathrm{D}}} $), (e)湍流传播率($ {\omega }_{{\mathrm{s}}} $), (f)湍流传播的通量和(g)密度涨落的平方的变化的条件平均
Fig. 8. Conditional averages of (a) ECRH power, (b) density gradient, (c) turbulent driven flux, (d) turbulence drive $ {\mathrm{r}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}\left({\omega }_{{\mathrm{D}}}\right) $, (e) turbulence spreading $ {\mathrm{r}}{\mathrm{a}}{\mathrm{t}}{\mathrm{e}}\left({\omega }_{{\mathrm{s}}}\right) $, (f) turbulent spreading flux, and (g) square of fluctuation intensity.
图 9 (a) ECRH功率, (b)粒子输运速度和(c)湍流传播平均射流度的变化的条件平均
Fig. 9. Conditional averages of (a) ECRH power, (b) particle transport velocity, (c) and mean jet velocity of turbulence spreading.
-
[1] Huang M, Rao J, Li B, Zhou J, Kang Z H, Wang H, Lu B, Xia D H, Wang C, Feng K, Wang M W, Chen G Y, Pu Y N, Lu Z H, Wang J Q, Duan X R, Liu Y 2012 EPJ Web Conf. 32 04012
Google Scholar
[2] Xu H D, Wang X J, Zhang J, Liu F K, Huang Y Y, Shan J F, Xu W Y, Li M H, Lohr J, Gorelov Y A, Anderson J P, Zhang Y, Wu D J, Hu H C, Yang Y, Feng J Q, Tang Y Y, Li B, Ma W D, Wu Z G, Wang J, Zhang L Y, Guo F, Sun H Z, Yan X S, EAST Team 2019 EPJ Web Conf. 203 04002
Google Scholar
[3] Xia D H, Chen X X, Li J T, Wang R M, Zheng W, the J-TEXT team 2024 EPJ Web Conf. 313 02003
Google Scholar
[4] Wagner D, Grünwald G, Leuterer F, Manini A, Monaco F, Münich M, Schütz H, Stober J, Zohm H, Franke T, Thumm M, Gantenbein G, Heidinger R, Meier A, Kasparek W, Lechte C, Litvak A, Denisov G G, Chirkov A V, Tai E M, Popov L G, NichiporenkoV O, Myasnikov V E, Solyanova E A, Malygin S A, Meo F, Woskov P 2008 Nucl. Fusion 48 054006
Google Scholar
[5] Kubo S 2012 EPJ Web Conf. 32 02001
Google Scholar
[6] Kajiwara K, Ikeda Y, Sakamoto K, Kasugai A, Seki M, Moriyama S, Takahashi K, Imai T, Mitsunaka Y, Fujii T 2003 Fusion Eng. Des. 65 493
Google Scholar
[7] Gnesin S, Decker J, Coda S, Goodman T P, Peysson Y, Mazon D 2012 Plasma Phys. Control. Fusion 54 035002
Google Scholar
[8] Mariani A, Mantica P, Brunner S, Fontana M, Karpushov A, Marini C, Porte L, Sauter O, the TCV Team, the EUROfusion MST1 Team 2019 Nucl. Fusion 59 126017
Google Scholar
[9] Yang Z J, Zhang Y P, Ren X H, Li F, Xu X, Yan W, Zhang X Y, Xia D H, Zhang Z C, GaoY, Zha X Q, Luo Q, Chen Z Y, Cheng Z F, Chen Z P, Gao L, Ding Y H 2021 Nucl. Fusion 61 086005
Google Scholar
[10] Wang S X, Liu H Q, Jie Y X, Zang Q, Lyu B, Zhang T, Zeng L, Zhang S B, Shi N, Lan T, Zou Z Y, Li W M, Yao Y, Wei X C, Lian H, Li G, Xu H D, Zhang X J, Wu B, Sun Y W, the EAST Team 2016 Plasma Sci. Technol. 19 015102
[11] Baschetti S, Bufferand H, Ciraolo G, Fedorczak N, Ghendrih P, Tamain P, Serre E, the EUROfusion MST1 team, the TCV team 2019 Nucl. Mater. Energy 19 200
Google Scholar
[12] Weiland J, Eriksson A, Nordman H, Zagorodny A 2007 Plasma Phys. Control. Fusion 49 A45
Google Scholar
[13] Luo L, Rafiq T, Kritz A H 2013 Comput. Phys. Commun. 184 2267
Google Scholar
[14] Doyle E J, Houlberg W A, Kamada Y, Mukhovatov V, Osborne T H, Polevoi A, Bateman G, Connor J W, Cordey J G, Fujita T, Garbet X, Hahm T S, Horton L D, Hubbard A E, Imbeaux F, Jenko F, Kinsey J E, Kishimoto Y, Li J, Luce T C, Martin Y, Ossipenko M, Parail V, Peeters A, Rhodes T L, Rice J E, Roach C M, Rozhansky V, Ryter F, Saibene G, Sartori R, Sips A C C, Snipes J A, Sugihara M, Synakowski E J, Takenaga H, Takizuka T, Thomsen K, Wade M R, Wilson H R, ITPA Transport Physics Topical Group, ITPA Confinement Database, Modelling Topical Group, ITPA Pedestal and Edge Topical Group 2007 Nucl. Fusion 47 S18
Google Scholar
[15] Ritz C P, Brower D L, Rhodes T L, Bengtson R D, Levinson S J, LuhmannJr N C, Peebles W A, Powers E J 1987 Nucl. Fusion 27 1125
Google Scholar
[16] Zhao K J, Dong J Q, Yan L W, Diamond P H, Cheng J, Hong W Y, Huang Z H, Xu M, Tynan G R, Itoh K, Itoh S -I, Fujisawa A, Nagashima Y, Inagaki S, Wang Z X, Wei L, Li Q, Ji X Q, Huang Y, Liu Yi, Zhou J, Song X M, Yang Q W, Ding X T, Duan X R, the HL-2A Team 2013 Nucl. Fusion 53 083011
Google Scholar
[17] Grenfell G, Van Milligen B P, Losada U, Ting W, Liu B, Silva C, Spolaore M, Hidalgo C, The TJ-II Team 2018 Nucl. Fusion 59 016018
[18] Gao J M, Cai L Z, Zou X L, Eich T, Adamek J, Cao C Z, Huang Z H, Ji X Q, Jiang M, Liu L, Lu J, Liu Y, Shi Z B, Thornton A J, Wu N, Xiao G L, Xu M, Yan L W, Yu L M, Yu D L, Yang Q W, Zhong W L, the HL-2A Team 2021 Nucl. Fusion 61 066024
Google Scholar
[19] Zhao K J, Nagashima Y, Guo Z B, Dong J Q, Yan L W, Itoh K, Itoh S I, Li X B, Li J Q, Fujisawa A, Inagaki S, Cheng J, Xu J Q, Kosuga Y, Sasaki M, Wang Z X, Zhang H Q, Chen Y Q, Cao X G, Yu D L, Liu Y, Song X M, Xia F, Wang S 2022 Plasma Sci. Technol. 25 015101
[20] Zhao K J, Shi Y J, Hahn S H, Diamond P H, Sun Y, Cheng J, Liu H, Lie N, Chen Z P, Ding Y H, Chen Z Y, Rao B, Leconte M, Bak J G, Cheng Z F, Gao L, Zhang X Q, Yang Z J, Wang N C, Wang L, Jin W, Yan L W, Dong J Q, Zhuang G, J-TEXT team 2015 Nucl. Fusion 55 073022
Google Scholar
[21] Zhao K J, Chen Z P, Shi Y J, Diamond P H, Dong J Q, Chen Z P, Ding Y H, Zhuang G, Liu Y B, Zhang H Q, Chen Y Q, Liu H, Cheng J, Nie L, Rao B, Cheng Z F, Gao L, Zhang X Q, Yang Z J, Wang N C, Wang L, Li J Q, Jin W, Xu J Q, Yan L W, Liang Y F, Xie Y Y, Liu B 2020 Nucl. Fusion 60 106030
Google Scholar
[22] Manz P, Ribeiro T T, Scott B D, Birkenmeier G, Carralero D, Fuchert G, Müller S H, Müller H W, Stroth U, Wolfrum E 2015 Phys. Plasmas 22 022308
Google Scholar
[23] Wu T, Diamond P H, Nie L, Xu M, Yu Y, Hong R J, Chen Y H, Xu J Q, Long T, Zhang Y, Yan Q H, Ke R, Cheng J, Li W, Huang Z H, Yan L W, Chu X, Wang Z H, Hidalgo C 2023 Nucl. Fusion 63 126001
Google Scholar
[24] Long T, Diamond P H, Ke R, Nie L, Xu M, Zhang X Y, Li B L, Chen Z P, Xu X, Wang Z H, Wu T, Tian W J, Yuan J B , Yuan B D, Gong S B, Xiao C Y , Gao J M, Hao Z G, Wang N C, Chen Z Y, Yang Z J, Gao L, Ding Y H, Pan Y, Chen W, Hao G Z, Li J Q, Zhong W L, Duan X R 2021 Nucl. Fusion 61 126066
下载:
计量
- 文章访问数: 368
- PDF下载量: 5
- 被引次数: 0
