-
High sensitivity optical gyroscopes, as an important component of aerospace navigation system, have become a research hotspot. The sensitivity of the classical optical gyroscope is restricted by the shot-noise-limit owing to the vacuum zero energy fluctuation. Therefore, the classical optical gyroscope cannot meet the growing demand of navigation, sensing and communication. In this work, a measurement scheme of quantum gyroscope based on frequency entangled source and Hong-Ou-Mandel (HOM) interference is proposed. In order to realize high-precision delay measurement, the interference visibility and width of HOM interferogram are regulated by changing the bandwidth of pump laser and the length of nonlinear crystal. However, traditional experimental regulation method is inefficient and time consuming. On the basis of the above scheme, a delay measurement scheme of HOM interference based on SSA-BP network is established. The SSA-BP network is used to simulate different bandwidths of pump laser and the lengths of nonlinear crystal to predict the interference visibility and width of HOM interferogram. The verification results show that the mean square error (MSE), the mean absolute error (MAE) and the mean absolute percentage error (MAPE) predicted by SSA-BP network are smallest. Based on the above SSA-BP network model, the interference visibility and width of HOM interferogram are
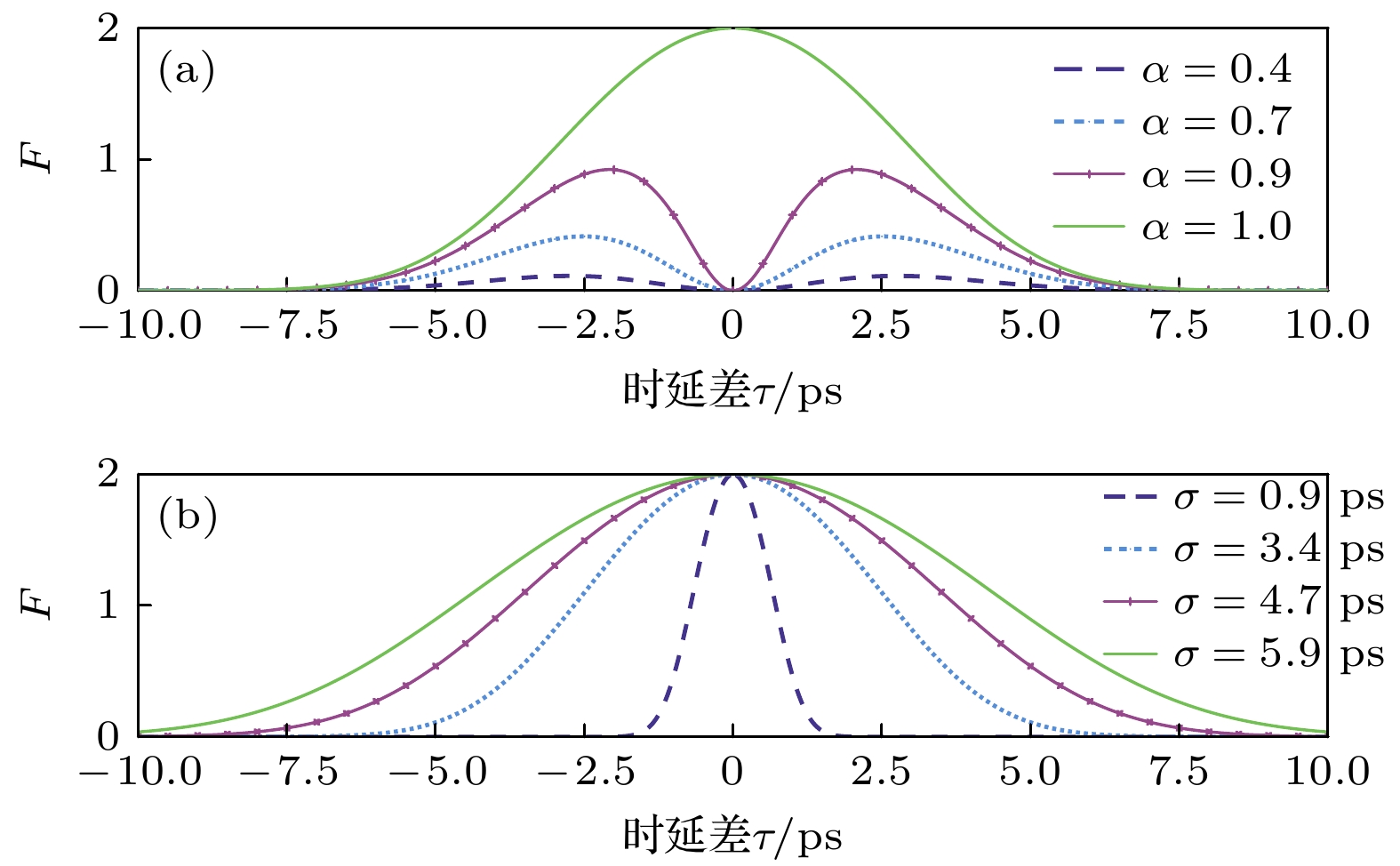
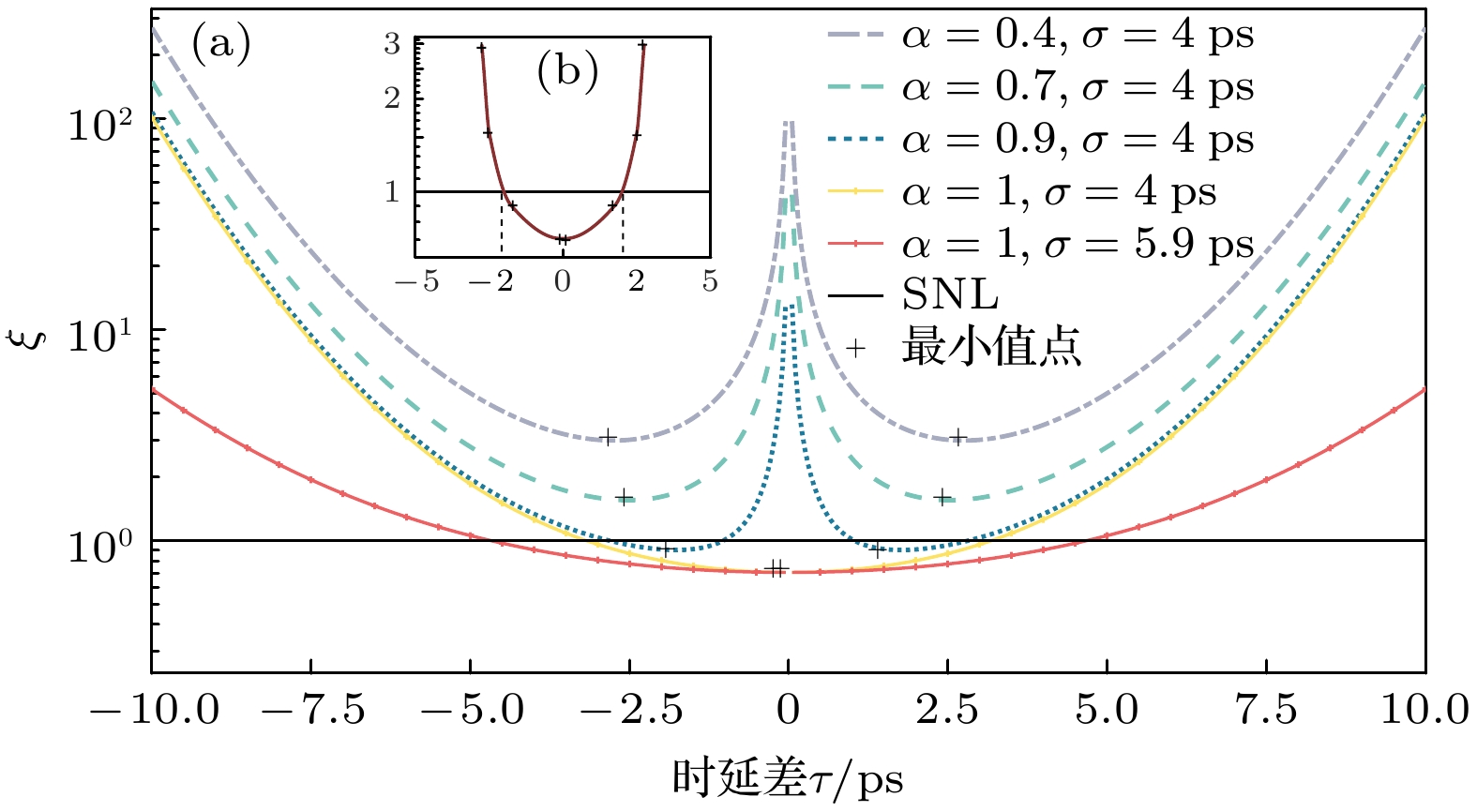
$\alpha = 1$ and$\sigma = 5.9\;{\text{ ps}}$ respectively. Combined with quantum Fisher information, the maximum value of F is obtained to be 1.999. Meanwhile, according to the Cramer-Rao bound theory, the minimum ratio of the uncertainty of the delay to the shot-noise-limit can reach 0.707, indicating that the precision of delay measurement is increased by 2 orders of magnitude. According to the relationship between delay and rotational angular velocity, the measurement sensitivity of the rotational angular velocity is improved by 2 orders of magnitude compared with that of the classical optical gyroscope. These results prove that the above quantum gyroscope scheme can realize the measurement sensitivity of rotational angular velocity beyond the shot-noise-limit. Therefore, the SSA-BP network model can provide theoretical support for the subsequent experimental verification of quantum gyroscopes based on HOM interference delay measurement, and is the technical basis for the development of quantum navigation, quantum sensing and quantum communication.-
Keywords:
- Hong-Ou-Mandel interference /
- time delay measurement /
- quantum gyroscope /
- sparrow search algorithm
[1] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press) pp271–281, 442–454
[2] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222
Google Scholar
[3] Kolkiran A, Agarwal G S 2007 Opt. Express 15 6798
Google Scholar
[4] 陈坤, 陈树新, 吴德伟, 杨春燕, 吴昊 2016 65 054203
Google Scholar
Chen K, Chen S X, Wu D W, Yang C Y, Wu H 2016 Acta Phys. Sin. 65 054203
Google Scholar
[5] Fink M, Steinlechner F, Handsteiner J, Dowling J P, Scheidl T, Ursin R 2019 New J. Phys. 21 053010
Google Scholar
[6] Bertocchi G, Alibart O, Ostrowsky D B, Tanzilli S, Baldi P 2006 J. Phys. B 39 1011
Google Scholar
[7] Yang Y, Xu L, Giovannetti V 2019 Sci. Rep. 9 10821
Google Scholar
[8] Napolitano M, Koschorreck M, Dubost B, Behbood N, Sewell R J, Mitchell M W 2011 Nature 471 486
Google Scholar
[9] Flammia S T, Caves C M, Geremia J M, Boixo S 2007 Phys. Rev. Lett. 98 90401
Google Scholar
[10] Caves C M 1981 Phys. Rev. D 23 1693
Google Scholar
[11] Barnett S M, Fabre C, Maıtre A 2003 Eur. Phys. J. D 22 513
Google Scholar
[12] Dowling J P 2008 Contemp. Phys. 49 125
Google Scholar
[13] Jiang L, Lukin M D, Rey A M 2007 Phys. Rev. A 76 53617
Google Scholar
[14] Lee C, Huang J, Deng H, et al. 2012 Front. Phys. 7 109
Google Scholar
[15] Giovannetti V, Lloyd S, Maccone L 2001 Nature 412 417
Google Scholar
[16] 张瑶, 张云波, 陈立 2021 70 168701
Google Scholar
Zhang Y, Zhang Y B, Chen L 2021 Acta Phys. Sin. 70 168701
Google Scholar
[17] 郎利影, 陆佳磊, 于娜娜, 席思星, 王雪光, 张雷, 焦小雪 2020 69 244204
Google Scholar
Lang L Y, Lu J L, Yu N N, Xi S X, Wang X G, Zhang L, Jiao X X 2020 Acta Phys.Sin. 69 244204
Google Scholar
[18] Xue J, Shen B 2020 Syst. Sci. Control Eng. 8 22
Google Scholar
[19] 孟彩霞, 吴迪, 雷雨 2022 大地测量与地球动力学 42 125
Meng C X, Wu D, Lei Y 2022 J. Geodesy and Geodynamics 42 125
[20] Maccone L, Shapiro J H, Wong F N C, Giovannetti V 2002 Phys. Rev. A 66 43813
Google Scholar
[21] Maccone L, Shapiro J H, Wong F N C, Giovannetti V 2002 Phys. Rev. Lett. 88 183602
Google Scholar
[22] 翟艺伟, 董瑞芳, 权润爱, 项晓, 刘涛, 张首刚 2021 70 120302
Google Scholar
Zhai Y W, Dong R F, Quan R A, Xiang X, Liu T, Zhang S G 2021 Acta Phys. Sin. 70 120302
Google Scholar
[23] Zheng Y, Yao A, Wang R 2004 Phys. Rev. Lett. 93 143901
Google Scholar
[24] Royfriened B 1998 Physics from Fisher Information (Cambridge: Cambridge University Press) pp22–62
[25] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[26] 牛明丽, 王月明, 李志坚 2022 71 090601
Google Scholar
Niu M L, Wang Y M, Li Z J 2022 Acta Phys. Sin. 71 090601
Google Scholar
[27] Lyons A, Knee G C, Bolduc E, Roger T, Leach J, Gauger E M, Faccio D 2018 Sci. Adv. 4 9416
Google Scholar
[28] Fisher R A 1925 Proc. Camb. Phil. Soc. 22 700
Google Scholar
[29] Holevo A S 2001 Statistical Structure of Quantum Theory (Berlin, Heidelberg: Springer) pp45–70
[30] Paris M G A 2009 arxiv: 0804.2981v3 [quant-ph]
[31] Pérez-Delgado C A, Kok P, Zwierz M 2010 Phys. Rev. Lett. 105 180402
Google Scholar
[32] 袁春华, 张可烨, 张卫平 2014 中国科学: 信息科学 44 345
Yuan C H, Zhang K Y, Zhang W P 2014 Sci. Sin. Informat. 44 345
[33] Lloyd S, Maccone L, Giovannetti V 2006 Phys. Rev. Lett. 96 10401
Google Scholar
[34] Efremov M A, Kazakov, A E, Chan K W, Law C K, Eberly J H, Fedorov M V 2004 Phys. Rev. A 69 52117
Google Scholar
[35] Volkov P A, Fedorov M V, Mikhailova Y M 2008 Phys. Rev. A 78 62327
Google Scholar
[36] Fedorov M V, Efremov M A, Volkov P A, Eberly J H 2006 J. Phys. B 39 S467
Google Scholar
-
图 1 基于频率纠缠光源与HOM干涉的量子陀螺仪原理框图
Figure 1. Principle block diagram of quantum gyroscope based on frequency entangled light source and HOM interference.
图 2 HOM干涉图谱
Figure 2. HOM interferogram.
图 3 SSA-BP神经网络拓扑结构
Figure 3. SSA-BP neural network topology.
图 4 不同BP网络预测数据集性能对比图 (a)
$\alpha $ 值; (b)$\sigma $ 值Figure 4. Performance comparison chart of different BP network prediction data sets: (a)
$\alpha $ values; (b)$\sigma $ values.
图 5 (a) 在不同的W值下,
$\alpha $ 随L的变化图; (b) 在不同的L值下,$\sigma $ 随W的变化图Figure 5. (a)
$\alpha $ as a function of L at different W; (b)$\sigma $ as a function of W at different L.
图 6 (a)
$\sigma = 4~{\text{ps}}$ , F随$\tau $ 的变化图; (b)$\alpha = 1$ , F随$\tau $ 的变化图Figure 6. (a) F as a function of delay
$\tau $ at$\sigma = 4{\text{ ps}}$ ; (b) F as a function of delay$\tau $ at$\alpha = 1$ 
图 7 (a) 参数
$ \xi $ 随$ \tau $ 值的变化; (b)$ \xi $ 最小值的变化图像Figure 7. (a) Parameter
$ \xi $ as a function of delay$ \tau $ ; (b) minimum value change image of$ \xi $ .表 1 不同BP网络预测
$\sigma $ 与$\alpha $ 的性能表Table 1. Performance table of different BP networks for predicting
$\sigma $ and$\alpha$ 神经网络类型 T/S 预测$\sigma $/ps 预测$\alpha $ MSE/10–6 MAE/10–3 MAPE/10–4 MSE/10–5 MAE/10–3 MAPE/10–2 BP 1.3 33.6 5 20 9.0 7 1.3 GA-BP 38.9 9.22 3 8.1 7.5 6 1.2 PSO-BP 158.1 21.7 4 10 7.0 6.1 1.18 SSA-BP 60.4 5.01 2 7.25 3.5 5 1.0 
DownLoad: CSV
-
[1] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press) pp271–281, 442–454
[2] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222
Google Scholar
[3] Kolkiran A, Agarwal G S 2007 Opt. Express 15 6798
Google Scholar
[4] 陈坤, 陈树新, 吴德伟, 杨春燕, 吴昊 2016 65 054203
Google Scholar
Chen K, Chen S X, Wu D W, Yang C Y, Wu H 2016 Acta Phys. Sin. 65 054203
Google Scholar
[5] Fink M, Steinlechner F, Handsteiner J, Dowling J P, Scheidl T, Ursin R 2019 New J. Phys. 21 053010
Google Scholar
[6] Bertocchi G, Alibart O, Ostrowsky D B, Tanzilli S, Baldi P 2006 J. Phys. B 39 1011
Google Scholar
[7] Yang Y, Xu L, Giovannetti V 2019 Sci. Rep. 9 10821
Google Scholar
[8] Napolitano M, Koschorreck M, Dubost B, Behbood N, Sewell R J, Mitchell M W 2011 Nature 471 486
Google Scholar
[9] Flammia S T, Caves C M, Geremia J M, Boixo S 2007 Phys. Rev. Lett. 98 90401
Google Scholar
[10] Caves C M 1981 Phys. Rev. D 23 1693
Google Scholar
[11] Barnett S M, Fabre C, Maıtre A 2003 Eur. Phys. J. D 22 513
Google Scholar
[12] Dowling J P 2008 Contemp. Phys. 49 125
Google Scholar
[13] Jiang L, Lukin M D, Rey A M 2007 Phys. Rev. A 76 53617
Google Scholar
[14] Lee C, Huang J, Deng H, et al. 2012 Front. Phys. 7 109
Google Scholar
[15] Giovannetti V, Lloyd S, Maccone L 2001 Nature 412 417
Google Scholar
[16] 张瑶, 张云波, 陈立 2021 70 168701
Google Scholar
Zhang Y, Zhang Y B, Chen L 2021 Acta Phys. Sin. 70 168701
Google Scholar
[17] 郎利影, 陆佳磊, 于娜娜, 席思星, 王雪光, 张雷, 焦小雪 2020 69 244204
Google Scholar
Lang L Y, Lu J L, Yu N N, Xi S X, Wang X G, Zhang L, Jiao X X 2020 Acta Phys.Sin. 69 244204
Google Scholar
[18] Xue J, Shen B 2020 Syst. Sci. Control Eng. 8 22
Google Scholar
[19] 孟彩霞, 吴迪, 雷雨 2022 大地测量与地球动力学 42 125
Meng C X, Wu D, Lei Y 2022 J. Geodesy and Geodynamics 42 125
[20] Maccone L, Shapiro J H, Wong F N C, Giovannetti V 2002 Phys. Rev. A 66 43813
Google Scholar
[21] Maccone L, Shapiro J H, Wong F N C, Giovannetti V 2002 Phys. Rev. Lett. 88 183602
Google Scholar
[22] 翟艺伟, 董瑞芳, 权润爱, 项晓, 刘涛, 张首刚 2021 70 120302
Google Scholar
Zhai Y W, Dong R F, Quan R A, Xiang X, Liu T, Zhang S G 2021 Acta Phys. Sin. 70 120302
Google Scholar
[23] Zheng Y, Yao A, Wang R 2004 Phys. Rev. Lett. 93 143901
Google Scholar
[24] Royfriened B 1998 Physics from Fisher Information (Cambridge: Cambridge University Press) pp22–62
[25] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[26] 牛明丽, 王月明, 李志坚 2022 71 090601
Google Scholar
Niu M L, Wang Y M, Li Z J 2022 Acta Phys. Sin. 71 090601
Google Scholar
[27] Lyons A, Knee G C, Bolduc E, Roger T, Leach J, Gauger E M, Faccio D 2018 Sci. Adv. 4 9416
Google Scholar
[28] Fisher R A 1925 Proc. Camb. Phil. Soc. 22 700
Google Scholar
[29] Holevo A S 2001 Statistical Structure of Quantum Theory (Berlin, Heidelberg: Springer) pp45–70
[30] Paris M G A 2009 arxiv: 0804.2981v3 [quant-ph]
[31] Pérez-Delgado C A, Kok P, Zwierz M 2010 Phys. Rev. Lett. 105 180402
Google Scholar
[32] 袁春华, 张可烨, 张卫平 2014 中国科学: 信息科学 44 345
Yuan C H, Zhang K Y, Zhang W P 2014 Sci. Sin. Informat. 44 345
[33] Lloyd S, Maccone L, Giovannetti V 2006 Phys. Rev. Lett. 96 10401
Google Scholar
[34] Efremov M A, Kazakov, A E, Chan K W, Law C K, Eberly J H, Fedorov M V 2004 Phys. Rev. A 69 52117
Google Scholar
[35] Volkov P A, Fedorov M V, Mikhailova Y M 2008 Phys. Rev. A 78 62327
Google Scholar
[36] Fedorov M V, Efremov M A, Volkov P A, Eberly J H 2006 J. Phys. B 39 S467
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2722
- PDF Downloads: 77
- Cited By: 0
