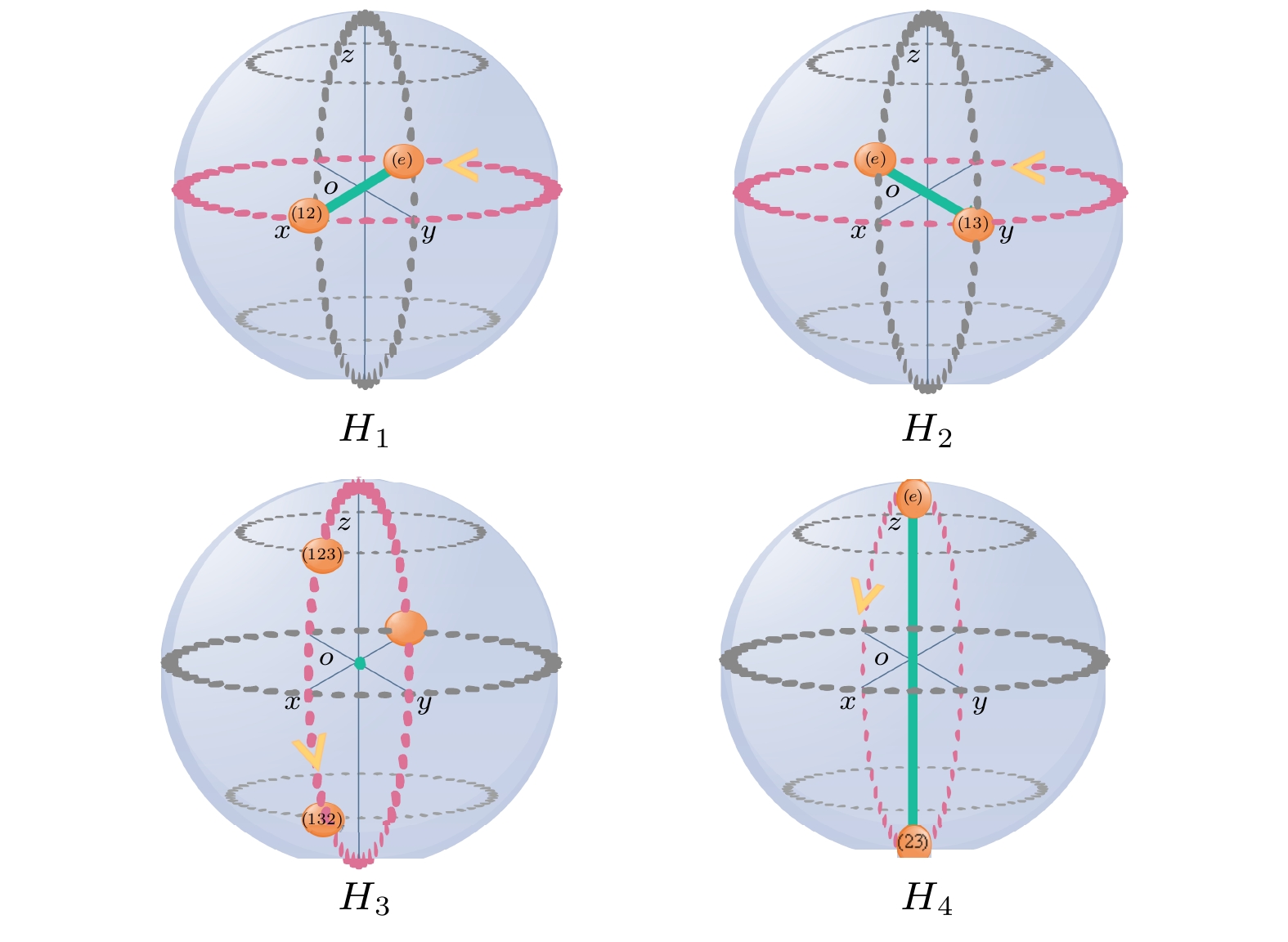
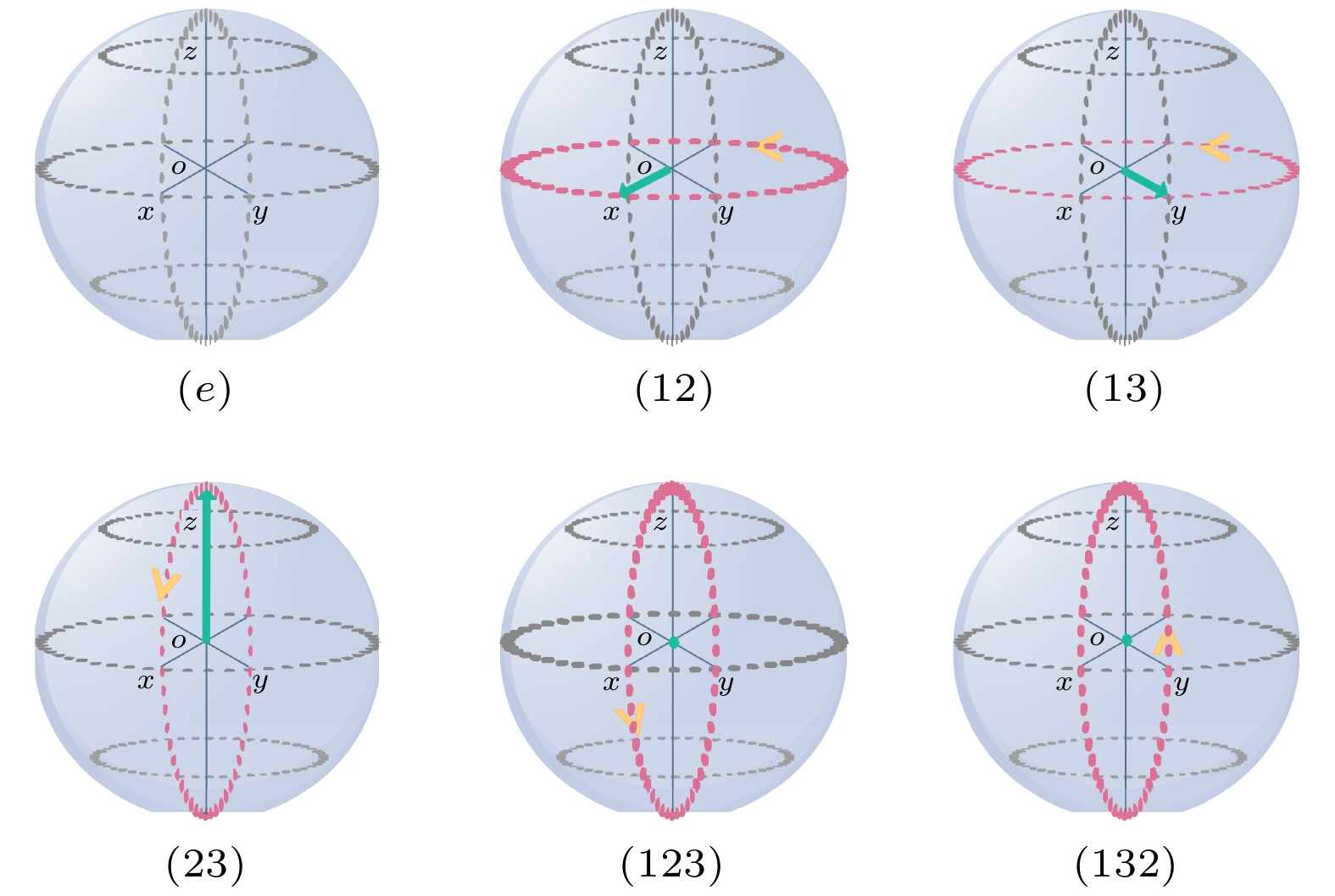
-
In quantum computing science, much attention has been paid to how to construct quantum search algorithms better, moreover, searching for new search algorithms based on quantum walk is still attracting scholars' continuous in-depth research and exploration. In this paper, a multi-particle quantum walk search algorithm based on permutation group is proposed by considering many aspects, such as reducing time consumption and increasing the accuracy and controllability of algorithm search. Firstly, the permutation group can be regarded as a closed loop in space, and the permutation set is defined. The data set of data points is mapped to the defined permutation set by isomorphism mapping, which makes the element data points in the permutation set form a one-to-one correspondence. Secondly, according to the given initial state and coin operator, the target data search is carried out on the ring by using the quantum walk of multiple particles in the search space of the data point set and the permutation set. Finally, the target data is found according to the function
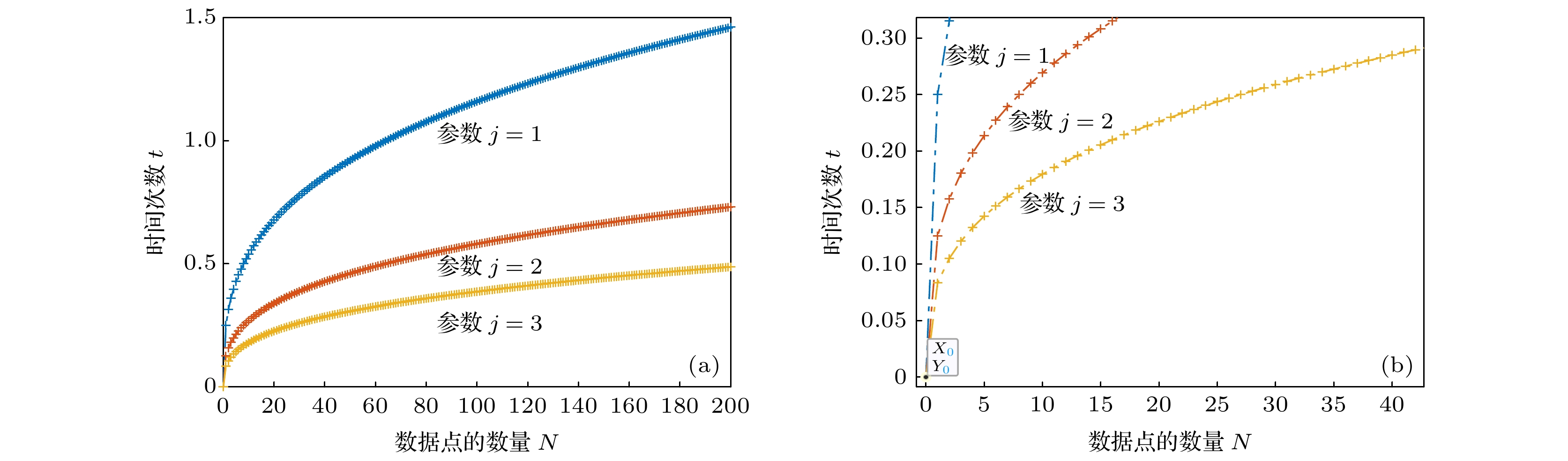
$\varPhi(w)=1 $ , and the value is stored by the quantum state, which is used to form the feedback control of the search algorithm. At the same time, the direction of quantum walking on the ring is controlled by controlling the coin operator, thus increasing the operability and accuracy of the search. In this paper, the quantum walk of multiple particles is used to search, and the analysis shows that the particle number parameter j is negatively correlated with the time complexity, but not negatively linear. The proposed quantum walk search algorithm conforms to the zero condition and the lower bound condition, and is not affected by the variable parameter j. Through numerical analysis, it is found that the time complexity of the quantum walk search algorithm is equivalent to$O(\sqrt[3]{N})$ , which improves the search efficiency compared with the Grover search algorithm.-
Keywords:
- search algorithm /
- quantum random walk /
- permutation group /
- isomorphic mapping
[1] Aharonov Y, Luiz D, Nicim Z 1993 Phys. Rev. A 48 1687
Google Scholar
[2] Farhi E, Gutmann S 1998 Phys. Rev. A 58 915
Google Scholar
[3] Godsil C, Kirkland S, Severini S, Smith J 2012 Phys. Rev. Lett. 109 050502
Google Scholar
[4] Bose S 2003 Phys. Rev. Lett. 91 207901
Google Scholar
[5] Childs A M 2009 Phys. Rev. Lett. 102 180501
Google Scholar
[6] Berry S D, Wang J B 2011 Phys. Rev. A 83 042317
[7] Zähringer F, Kirchmair G, Gerritsma R, Solano E, Blatt R, Roos C F 2010 Phys. Rev. Lett. 104 100503
Google Scholar
[8] Ma H Y, Zhang X, Xu P A, Liu F 2020 Wirel. Pers. Commun. 113 2203
Google Scholar
[9] Wocjan P, Abeyesinghe A 2008 Phys. Rev. A 78 042336
Google Scholar
[10] Orsucci D, Briegel H J, Dunjko V 2018 Quantum 2 105
Google Scholar
[11] Chakraborty S, Novo L, Ambainis A, Omar Y 2016 Phys. Rev. Lett. 116 100501
Google Scholar
[12] Chakraborty S, Novo L, Di Giorgio S, Omar Y 2017 Phys. Rev. Lett. 119 220503
Google Scholar
[13] Chang C R, Lin Y C, Chiu K L, Huang T W 2020 AAPPS Bull. 30 9
Google Scholar
[14] Childs A M 2010 Commun. Math. Phys. 294 581
Google Scholar
[15] Shenvi N, Kempe J, Whaley K B 2003 Phys. Rev. A 67 052307
Google Scholar
[16] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[17] Caruso F 2014 New J. Phys. 16 055015
Google Scholar
[18] Liu F, Zhang X, Xu P A, He Z X, Ma H Y 2020 Int. J. Theor. Phys. 59 3491
Google Scholar
[19] Dunjko V, Briegel H J 2015 New J. Phys. 17 073004
Google Scholar
[20] Glos A, Krawiec A, Kukulski R, PuchaPuchała Z 2018 Quantum Inf. Process. 17 1
Google Scholar
[21] Mülken O, Blumen A 2011 Phys. Rep. 502 37
Google Scholar
[22] Long G L, Wang C, Deng F G, Zheng C 2013 Conference on Coherence and Quantum Optics Rochester, New York, USA, June 17–20, 2013 ppM6–42
[23] Kempf A, Portugal R 2009 Phys. Rev. A 79 052317
Google Scholar
[24] Zhou L, Sheng Y B, Long G L 2020 Sci. Bull. 65 12
Google Scholar
[25] Zhou Z, Sheng Y, Niu P, Yin L, Long G L, Hanzo L 2020 Sci. China: Phys. Mech. Astron. 63 1
Google Scholar
[26] Long G L 2001 Phys. Rev. A 64 022307
Google Scholar
[27] Zhou N R, Huang L X, Gong L H, Zeng Q W 2020 Quantum Inf. Process. 19 1
Google Scholar
[28] Zhou N R, Zhu K N, Zou X F 2019 Ann. Phys. 531 1800520
Google Scholar
[29] Zhou N R, Zhu K N, Bi W, Gong L H 2019 Quantum Inf. Process. 18 1
Google Scholar
[30] Li H H, Gong L H, Zhou N R 2020 Chin. Phys. B 29 110304
Google Scholar
[31] Sheng Y B, Zhou L 2018 Phys. Rev. A 98 052343
Google Scholar
[32] Sheng Y B, Zhou L 2017 Sci. Bull. 62 1025
Google Scholar
[33] 张禾瑞 1997 近世代数基础 (修订本) (北京: 高等教育出版社) 第50页
Zhang H R 1997 Base of Recent Generations (Vol. 19) (Beijing: Higher Education Press) p50 (in Chinese)
[34] Schreiber A, Cassemiro K N, Potoček V, Gábris A, Mosley P J, Andersson E, Jex I, Silberhorn Ch 2010 Phys. Rev. Lett. 104 050502
Google Scholar
[35] Diaconis P, Rockmore D 1990 J. Am. Math. Soc. 3 297
Google Scholar
[36] Toyama F M, Van Dijk W, Nogami Y 2013 Quantum Inf. Process. 12 p1897
Google Scholar
-
图 1 置换群
$ S_{3} $ 中每个元素的旋转方位图Figure 1. Diagram of the rotation position of each element in the permutation group
$ S_{3} $ .
图 2 在每个子群中各个元素之间的旋转关系图
Figure 2. Diagram of the rotation relationship between the elements in each subgroup.
图 3 集合W,
$ W _{-1} $ 和$ W _{\lambda} $ 元素之间的对应关系Figure 3. Corresponding relationship between elements of the sets W,
$ W _{-1} $ and$ W _{\lambda} $ .
图 4 量子行走的过程
Figure 4. Process of quantum walk.
图 5 两种搜索算法时间按复杂度的对比
Figure 5. Comparison of the time complexity of two search algorithms.
图 6 参数j对搜索算法时间复杂度的影响
Figure 6. Influence of parameter j on the time complexity of search algorithm.
表 1 置换集合元素分布情况
Table 1. Distribution of the elements in permutation set.
子群 子群族 群内所在元素 $H_{1}$ $H_{1}^{1}$ $p(1, 1, 1), \; p(1, 1, 2)$ $\vdots$ $\vdots$ $H_{1}^{j_{1}}$ $p(1, j_{1}, 1)$, $p(1, j_{1}, 2)$ $H_{i}$ $H_{i}^{1}$ $p(i, 1, 1), \; p(i, 1, 2)$ $\vdots$ $\vdots$ $H_{i}^{j_{i}}$ $p(i, j_{i}, 1)$, $p(i, j_{i}, 2)$ 
DownLoad: CSV
表 2 数据仿真结果
Table 2. Numerical simulation results.
数据点数量N $ j = 1 $ $ j = 2$ $ j = 3 $ 1024 3 2 1 2048 4 2 2 4096 4 2 2 8192 6 3 2 16384 7 4 3 32768 8 4 3
DownLoad: CSV
-
[1] Aharonov Y, Luiz D, Nicim Z 1993 Phys. Rev. A 48 1687
Google Scholar
[2] Farhi E, Gutmann S 1998 Phys. Rev. A 58 915
Google Scholar
[3] Godsil C, Kirkland S, Severini S, Smith J 2012 Phys. Rev. Lett. 109 050502
Google Scholar
[4] Bose S 2003 Phys. Rev. Lett. 91 207901
Google Scholar
[5] Childs A M 2009 Phys. Rev. Lett. 102 180501
Google Scholar
[6] Berry S D, Wang J B 2011 Phys. Rev. A 83 042317
[7] Zähringer F, Kirchmair G, Gerritsma R, Solano E, Blatt R, Roos C F 2010 Phys. Rev. Lett. 104 100503
Google Scholar
[8] Ma H Y, Zhang X, Xu P A, Liu F 2020 Wirel. Pers. Commun. 113 2203
Google Scholar
[9] Wocjan P, Abeyesinghe A 2008 Phys. Rev. A 78 042336
Google Scholar
[10] Orsucci D, Briegel H J, Dunjko V 2018 Quantum 2 105
Google Scholar
[11] Chakraborty S, Novo L, Ambainis A, Omar Y 2016 Phys. Rev. Lett. 116 100501
Google Scholar
[12] Chakraborty S, Novo L, Di Giorgio S, Omar Y 2017 Phys. Rev. Lett. 119 220503
Google Scholar
[13] Chang C R, Lin Y C, Chiu K L, Huang T W 2020 AAPPS Bull. 30 9
Google Scholar
[14] Childs A M 2010 Commun. Math. Phys. 294 581
Google Scholar
[15] Shenvi N, Kempe J, Whaley K B 2003 Phys. Rev. A 67 052307
Google Scholar
[16] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[17] Caruso F 2014 New J. Phys. 16 055015
Google Scholar
[18] Liu F, Zhang X, Xu P A, He Z X, Ma H Y 2020 Int. J. Theor. Phys. 59 3491
Google Scholar
[19] Dunjko V, Briegel H J 2015 New J. Phys. 17 073004
Google Scholar
[20] Glos A, Krawiec A, Kukulski R, PuchaPuchała Z 2018 Quantum Inf. Process. 17 1
Google Scholar
[21] Mülken O, Blumen A 2011 Phys. Rep. 502 37
Google Scholar
[22] Long G L, Wang C, Deng F G, Zheng C 2013 Conference on Coherence and Quantum Optics Rochester, New York, USA, June 17–20, 2013 ppM6–42
[23] Kempf A, Portugal R 2009 Phys. Rev. A 79 052317
Google Scholar
[24] Zhou L, Sheng Y B, Long G L 2020 Sci. Bull. 65 12
Google Scholar
[25] Zhou Z, Sheng Y, Niu P, Yin L, Long G L, Hanzo L 2020 Sci. China: Phys. Mech. Astron. 63 1
Google Scholar
[26] Long G L 2001 Phys. Rev. A 64 022307
Google Scholar
[27] Zhou N R, Huang L X, Gong L H, Zeng Q W 2020 Quantum Inf. Process. 19 1
Google Scholar
[28] Zhou N R, Zhu K N, Zou X F 2019 Ann. Phys. 531 1800520
Google Scholar
[29] Zhou N R, Zhu K N, Bi W, Gong L H 2019 Quantum Inf. Process. 18 1
Google Scholar
[30] Li H H, Gong L H, Zhou N R 2020 Chin. Phys. B 29 110304
Google Scholar
[31] Sheng Y B, Zhou L 2018 Phys. Rev. A 98 052343
Google Scholar
[32] Sheng Y B, Zhou L 2017 Sci. Bull. 62 1025
Google Scholar
[33] 张禾瑞 1997 近世代数基础 (修订本) (北京: 高等教育出版社) 第50页
Zhang H R 1997 Base of Recent Generations (Vol. 19) (Beijing: Higher Education Press) p50 (in Chinese)
[34] Schreiber A, Cassemiro K N, Potoček V, Gábris A, Mosley P J, Andersson E, Jex I, Silberhorn Ch 2010 Phys. Rev. Lett. 104 050502
Google Scholar
[35] Diaconis P, Rockmore D 1990 J. Am. Math. Soc. 3 297
Google Scholar
[36] Toyama F M, Van Dijk W, Nogami Y 2013 Quantum Inf. Process. 12 p1897
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6874
- PDF Downloads: 214
- Cited By: 0
