-
基于纠缠光子对的Hong-Ou-Mandel (HOM)干涉仪在量子精密测量等领域有着重要应用. 本文提出了利用一个级联HOM干涉仪实现多个独立时延参数的同时测量方案. 通过理论分析得出纠缠光子对经过多个50∶50分束器级联传输后, 其HOM二阶量子干涉图谱中凹陷位置与各级传输路径间独立时延参数的对应关系, 因此可通过记录各个凹陷位置的时延值实现多个独立时延参数的同时测量. 在此基础上搭建了基于频率一致纠缠光子对的二级级联HOM干涉测量装置, 通过实验上得到的具有两个对称凹陷的二阶量子干涉图谱, 实现了两级传输路径间两个独立时延参数
$ {\tau }_{1} $ 和$ {\tau }_{2} $ 的同时测量, 并分别获得了109 fs和98 fs的测量精度. 上述研究结果为HOM干涉仪在多参量量子精密测量系统中的扩展应用奠定基础.-
关键词:
- Hong-Ou-Mandel干涉仪 /
- 纠缠光子对 /
- 多时延参数 /
- 同时测量
The Hong-Ou-Mandel (HOM) interferometer using entangled photon source possesses important applications in quantum precision measurement and relevant areas. In this paper, a simultaneous measurement scheme of multiple independent delay parameters based on a cascaded HOM interferometer is proposed. The cascaded HOM interferometer is composed of $ n $ concatenated 50∶50 beam splitters and independent delay parameters$ {\tau }_{1} $ ,$ {\tau }_{2} $ , ···,$ {\tau }_{n} $ . The numbers$ n=1, 2\;\mathrm{a}\mathrm{n}\mathrm{d}\;3 $ refer to the standard HOM interferometer, the second-cascaded HOM interferometer, and the third-cascaded HOM interferometer, respectively. Through the theoretical study of the cascaded HOM interference effect based on frequency entangled photon pairs, it can be concluded that there is a corresponding relationship between the dip position and the independent delay parameter in the second-order quantum interferogram. In the standard HOM interferometer, there is a dip in the second-order quantum interferogram, which can realize the measurement of delay parameter$ {\tau }_{1} $ . In the second-cascaded HOM interferometer, there are two symmetrical dips in the second-order quantum interferogram, which can realize the simultaneous measurement of two independent delay parameters$ {\tau }_{1} $ and$ {\tau }_{2} $ . By analogy, in the third-cascaded HOM interferometer, there are six symmetrical dips in the second-order quantum interferogram, which can realize the simultaneous measurement of three independent delay parameters$ {\tau }_{1} $ ,$ {\tau }_{2} $ and$ {\tau }_{3} $ . Therefore, multiple independent delay parameters can be measured simultaneously based on a cascaded HOM interferometer.In the experiment, the second-cascaded HOM interferometer based on frequency entangled photon source is built. The second-order quantum interferogram of the second-cascaded HOM interferometer is obtained by the coincidence measurement device. Two independent delay parameters $ {\tau }_{1} $ and$ {\tau }_{2} $ are measured simultaneously by recording the positions of two symmetrical dips, which are in good agreement with the theoretical results. At an averaging time of 3000 s, the measurement accuracy of two delay parameters$ {\tau }_{1} $ and$ {\tau }_{2} $ can reach 109 and 98 fs, respectively. These results lay a foundation for extending the applications of HOM interferometer in multi-parameter quantum systems.-
Keywords:
- Hong-Ou-Mandel interferometer /
- entangled photon pairs /
- multiple delay parameters /
- simultaneous measurement
[1] Hong C K, Ou Z Y, Mandel L 1987 Phys. Rev. Lett. 59 2044
Google Scholar
[2] Ou Z Y, Hong C K, Mandel L 1987 Opt. Commun. 63 118
Google Scholar
[3] Nagata T, Okamoto R, O’Brien J L, Sasaki K, Takeuchi S 2007 Science 316 726
Google Scholar
[4] Pan J W, Chen Z B, Lu C Y, Weinfurter H, Zeilinger A, Zukowski M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[5] Carrasco S, Torres J P, Toener L 2004 Opt. Lett. 29 20
Google Scholar
[6] Quan R A, Zhai Y W, Wang M M, Hou F Y, Wang S F, Xiang X, Liu T, Zhang S G, Dong R F 2016 Sci. Rep. 6 30453
Google Scholar
[7] Ma X S, Zotter S, Kofler J, Ursin R, Jennewein T, Brukner C, Zeilinger A 2012 Nat. Phys. 8 6
Google Scholar
[8] Quan R A, Dong R F, Zhai Y W, Hou F Y, Xiang X, Zhou H, Lü C L, Wang Z, You L X, Liu T, Zhang S G 2019 Opt. Lett. 44 3
Google Scholar
[9] Schwarz L, van Enk S J 2011 Phys. Rev. Lett. 106 180501
Google Scholar
[10] Jozsa R, Abrams D S, Dowling J P, Williams C P 2000 Phys. Rev. Lett. 85 2010
Google Scholar
[11] 李银海, 许昭怀, 王双, 许立新, 周志远, 史保森 2017 68 120302
Google Scholar
Li Y H, Xu Z H, Wang S, Xu L X, Zhou Z Y, Shi B S 2017 Acta Phys. Sin. 68 120302
Google Scholar
[12] Giovannetti V, Lloyd S, Maccone L 2001 Nature 412 417
Google Scholar
[13] Giovannetti V, Lloyd S, Maccone L, Wong F N C 2001 Phys. Rev. Lett. 87 117902
Google Scholar
[14] Baek S Y, Cho Y W, Kim Y H 2009 Opt. Express 17 19241
Google Scholar
[15] Grice W P, Walmsley I A 1997 Phys. Rev. A 56 1627
Google Scholar
[16] Kaltenbaek R, Blauensteiner B, Żukowski M, Aspelmeyer M, Zeilinger A 2006 Phys. Rev. Lett. 96 240502
Google Scholar
[17] Branning D, Migdall A L, Sergienko A V 2000 Phys. Rev. A 62 063808
Google Scholar
[18] Dauler E, Jaeger G, Muller A, Migdall A 1999 J. Res. Natl. Inst. Stand. Technol. 104 1
Google Scholar
[19] Lyons A, Knee G C, Bolduc E, Roger T, Leach J, Gauger E M, Faccio D 2018 Sci. Adv. 4 5
Google Scholar
[20] Zhai Y W, Dong R F, Li B H, Quan R A, Wang M M, Hou F Y, Liu T, Zhang S G 2017 J. Phys. B: At. Mol. Opt. Phys. 50 125502
Google Scholar
[21] Yang Y, Xu L P, Giovannetti V 2019 Sci. Rep. 9 1
Google Scholar
[22] Yang Y, Xu L P, Giovannetti V 2019 Phys. Rev. A 100 063810
Google Scholar
[23] Giovannetti V, Maccone L, Shapiro J H, Wong F N C 2002 Phys. Rev. A 66 043813
Google Scholar
[24] Quan R A, Wang M M, Hou F Y, Tai Z Y, Dong R F 2015 Appl. Phys. B 118 431
Google Scholar
-
图 1 基于频率纠缠光源的多级级联HOM干涉仪的原理框图
Fig. 1. Schematic of multi-cascaded HOM interferometer based on frequency entangled source.
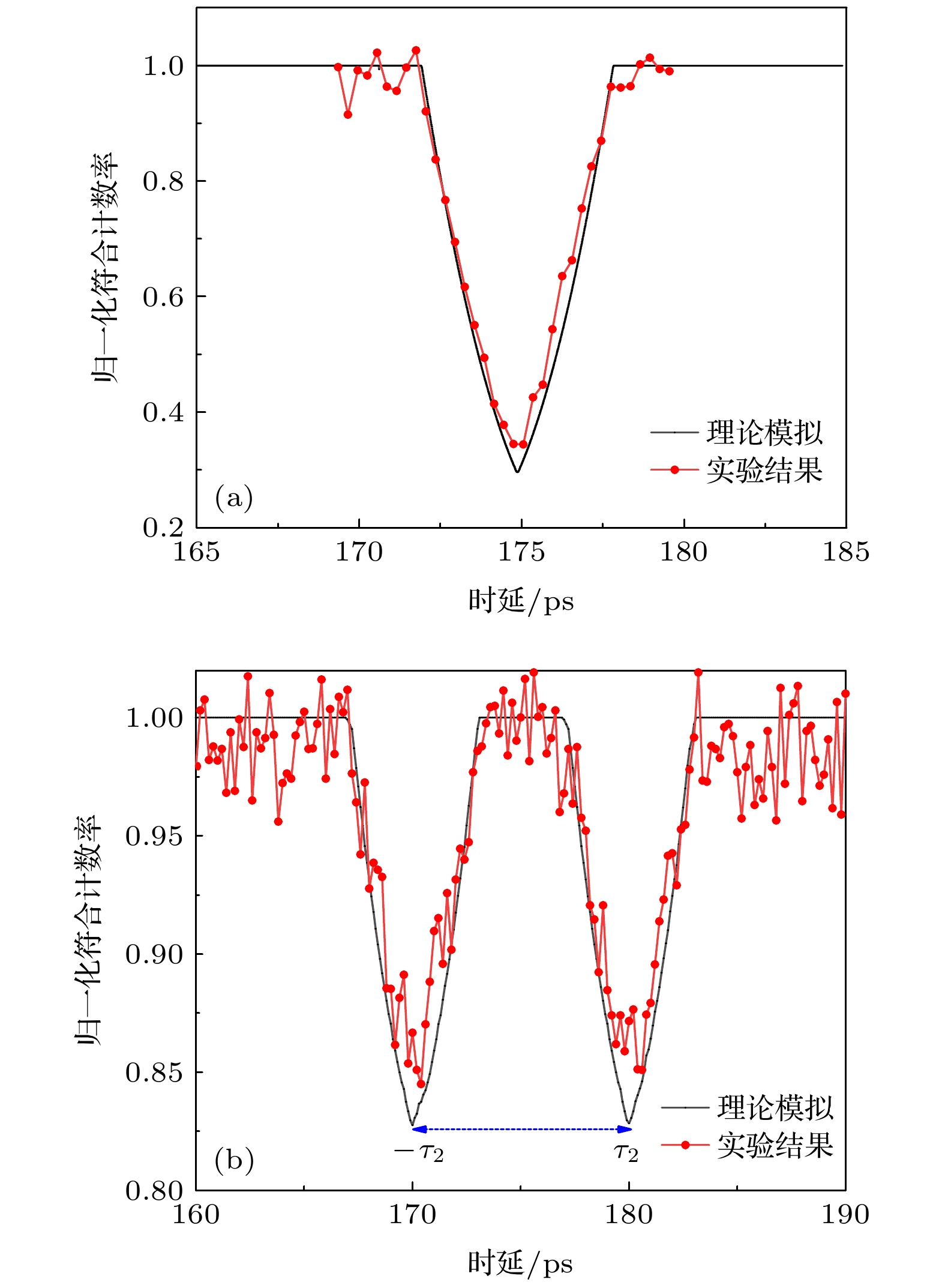
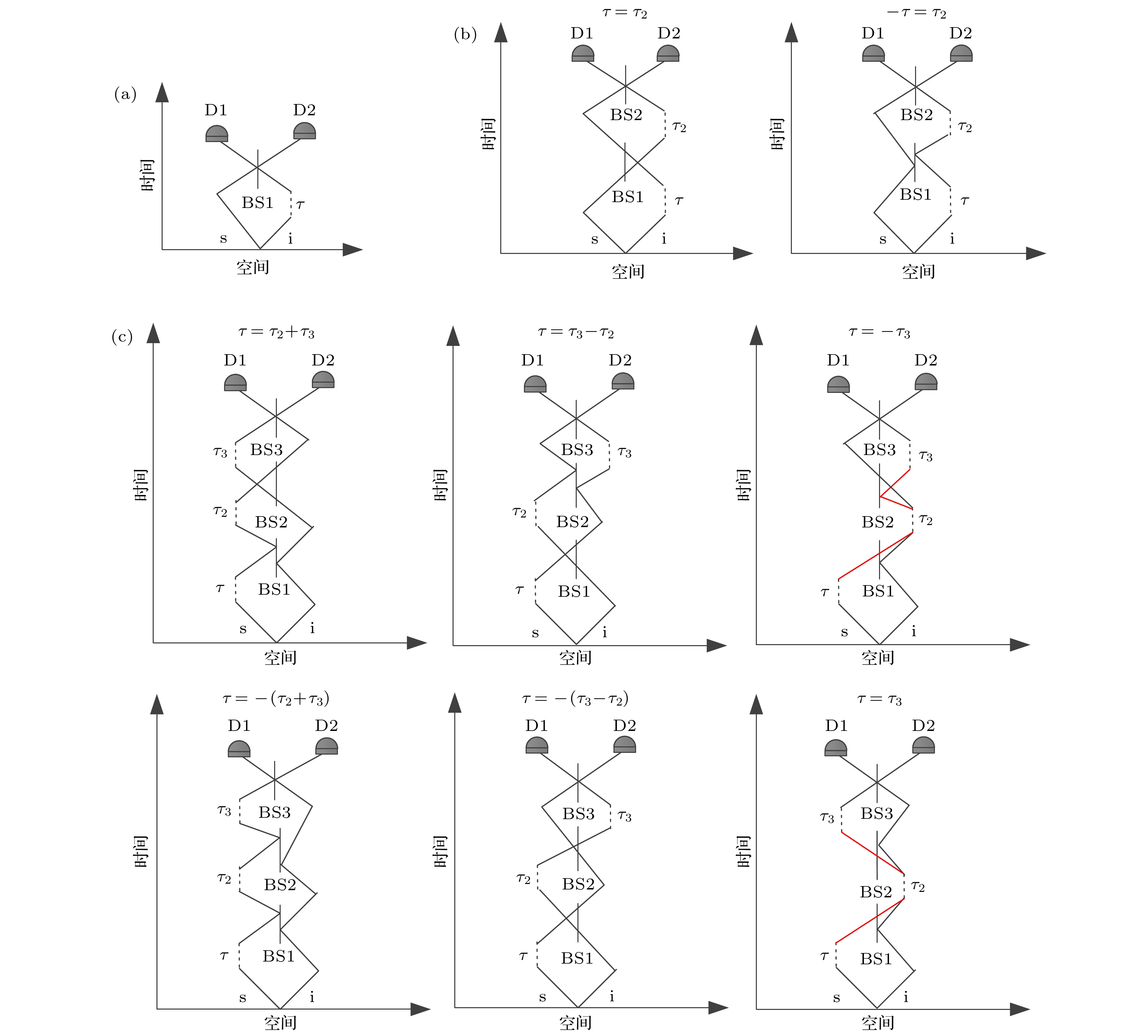
图 2 基于频率纠缠光子对的多级级联HOM干涉仪的二阶量子干涉图谱 (a) 标准HOM干涉仪; (b) 二级级联HOM干涉仪; (c) 三级级联HOM干涉仪
Fig. 2. The second-order quantum interferograms of multi-cascaded HOM interferometer based on frequency entangled photon pairs: (a) HOM interferometer; (b) the second-cascaded HOM interferometer; (c) the third-cascaded HOM interferometer.
图 3 基于频率纠缠光子对的二级级联HOM干涉仪实验装置图(HWP, 半波片; PPKTP, 周期极化磷酸氧钛钾晶体; DM, 分色镜; Lens, 透镜组; FC, 光纤耦合器; FPBS, 光纤偏振分束器; 50∶50 FBS, 50∶50光纤分束器; FPC, 光纤偏振控制器; MDL, 电动可调光学延迟线; ODL, 手动可调光学延迟线; SNSPD, 超导纳米线单光子探测器)
Fig. 3. Experimental setup of the second-cascaded HOM interferometer based on frequency entangled photon pairs. HWP, half-wave plate; PPKTP, periodically poled KTP; DM, dichroic mirror; Lens, a set of lenses; FC, fiber connection; FPBS, fiber-based polarization beam splitter; 50∶50 FBS, 50∶50 fiber beam splitter; FPC, fiber polarization controller; MDL, motorized delay line; ODL, optical delay line; SNSPD, super-conductor nanowire single photon detector.
图 4 频率一致纠缠光子对的二阶量子干涉图谱实验结果 (a) 标准HOM干涉仪; (b) 二级级联HOM干涉仪
Fig. 4. Experimental results of second-order quantum interferograms based on frequency entangled photon pairs: (a) HOM interferometer; (b) the second-cascaded HOM interferometer.
图 5 基于二级级联HOM干涉仪的两个独立时延参数
$ {\tau }_{1} $ 和$ {\mathrm{\tau }}_{2} $ 的测量精度Fig. 5. Measurement accuracy of delay
$ {\tau }_{1} $ and$ {\tau }_{2} $ based on the second-cascaded HOMI.
图 6 时延参数
$ {\tau }_{2} $ 的测量值与环境温度及测量时间的变化关系Fig. 6. Delay movements
$ {\tau }_{2} $ and the temperature variations versus the measuring time.
图 SA1 纠缠光子对的干涉费曼图 (a) 标准HOM干涉仪; (b) 二级级联HOM干涉仪; (c) 三级级联HOM干涉仪
Fig. SA1. The Feynman-like diagrams of entangled photon pairs: (a) HOM interferometer; (b) the second-cascaded HOM interferometer; (c) the third-cascaded HOM interferometer.
-
[1] Hong C K, Ou Z Y, Mandel L 1987 Phys. Rev. Lett. 59 2044
Google Scholar
[2] Ou Z Y, Hong C K, Mandel L 1987 Opt. Commun. 63 118
Google Scholar
[3] Nagata T, Okamoto R, O’Brien J L, Sasaki K, Takeuchi S 2007 Science 316 726
Google Scholar
[4] Pan J W, Chen Z B, Lu C Y, Weinfurter H, Zeilinger A, Zukowski M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[5] Carrasco S, Torres J P, Toener L 2004 Opt. Lett. 29 20
Google Scholar
[6] Quan R A, Zhai Y W, Wang M M, Hou F Y, Wang S F, Xiang X, Liu T, Zhang S G, Dong R F 2016 Sci. Rep. 6 30453
Google Scholar
[7] Ma X S, Zotter S, Kofler J, Ursin R, Jennewein T, Brukner C, Zeilinger A 2012 Nat. Phys. 8 6
Google Scholar
[8] Quan R A, Dong R F, Zhai Y W, Hou F Y, Xiang X, Zhou H, Lü C L, Wang Z, You L X, Liu T, Zhang S G 2019 Opt. Lett. 44 3
Google Scholar
[9] Schwarz L, van Enk S J 2011 Phys. Rev. Lett. 106 180501
Google Scholar
[10] Jozsa R, Abrams D S, Dowling J P, Williams C P 2000 Phys. Rev. Lett. 85 2010
Google Scholar
[11] 李银海, 许昭怀, 王双, 许立新, 周志远, 史保森 2017 68 120302
Google Scholar
Li Y H, Xu Z H, Wang S, Xu L X, Zhou Z Y, Shi B S 2017 Acta Phys. Sin. 68 120302
Google Scholar
[12] Giovannetti V, Lloyd S, Maccone L 2001 Nature 412 417
Google Scholar
[13] Giovannetti V, Lloyd S, Maccone L, Wong F N C 2001 Phys. Rev. Lett. 87 117902
Google Scholar
[14] Baek S Y, Cho Y W, Kim Y H 2009 Opt. Express 17 19241
Google Scholar
[15] Grice W P, Walmsley I A 1997 Phys. Rev. A 56 1627
Google Scholar
[16] Kaltenbaek R, Blauensteiner B, Żukowski M, Aspelmeyer M, Zeilinger A 2006 Phys. Rev. Lett. 96 240502
Google Scholar
[17] Branning D, Migdall A L, Sergienko A V 2000 Phys. Rev. A 62 063808
Google Scholar
[18] Dauler E, Jaeger G, Muller A, Migdall A 1999 J. Res. Natl. Inst. Stand. Technol. 104 1
Google Scholar
[19] Lyons A, Knee G C, Bolduc E, Roger T, Leach J, Gauger E M, Faccio D 2018 Sci. Adv. 4 5
Google Scholar
[20] Zhai Y W, Dong R F, Li B H, Quan R A, Wang M M, Hou F Y, Liu T, Zhang S G 2017 J. Phys. B: At. Mol. Opt. Phys. 50 125502
Google Scholar
[21] Yang Y, Xu L P, Giovannetti V 2019 Sci. Rep. 9 1
Google Scholar
[22] Yang Y, Xu L P, Giovannetti V 2019 Phys. Rev. A 100 063810
Google Scholar
[23] Giovannetti V, Maccone L, Shapiro J H, Wong F N C 2002 Phys. Rev. A 66 043813
Google Scholar
[24] Quan R A, Wang M M, Hou F Y, Tai Z Y, Dong R F 2015 Appl. Phys. B 118 431
Google Scholar
下载:
计量
- 文章访问数: 5745
- PDF下载量: 151
- 被引次数: 0
