-
General higher-order rogue wave solutions to the space-shifted
$\mathcal{PT}$ -symmetric nonlocal nonlinear Schrödinger equation are constructed by employing the Kadomtsev-Petviashvili hierarchy reduction method. The analytical expressions for rogue wave solutions of any Nth-order are given through Schur polynomials. We first analyze the dynamics of the first-order rogue waves, and find that the maximum amplitude of the rogue waves can reach any height larger than three times of the constant background amplitude. The effects of the space-shifted factor$x_0$ of the$\mathcal{PT}$ -symmetric nonlocal nonlinear Schrödinger equation in the first-order rogue wave solutions are studied, which only changes the center positions of the rogue waves. The dynamical behaviours and patterns of the second-order rogue waves are also analytically investigated. Then the relationships between Nth-order rogue wave patterns and the parameters in the analytical expressions of the rogue wave solutions are given, and the several different patterns of the higher-order rogue waves are further shown.-
Keywords:
- rogue waves /
- $\mathcal{PT}$-symmetric nonlocal nonlinear Schrödinger equation /
- Kadomtsev-Petviashvili hierarchy reduction method
[1] Ablowitz M J, Segur H 1981 Solitons and Inverse Scattering Transform (Philadelphia: SIAM)
[2] Yang J K 2010 Nonlinear Waves in Integrable and Nonintegrable Systems (Philadelphia: SIAM)
[3] Bender C M, Boettcher S 1988 Phys. Rev. Lett. 80 5243
Google Scholar
[4] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201
Google Scholar
[5] Mostafazadeh A 2003 J. Phys. A: Math. Gen. 36 7081
Google Scholar
[6] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
Google Scholar
[7] Regensburger A, Bersch C, Miri M A, Onishchukov G, Christodoulides D N, Peschel U 2012 Nature 488 167
Google Scholar
[8] Makris K G, El-Ganainy R, Christodoulides D N, Musslimani Z H 2008 Phys. Rev. Lett. 100 103904
Google Scholar
[9] Ruter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192
Google Scholar
[10] Regensburger A, Miri M A, Bersch C, Nager J, Onishchukov G, Christodoulides D N, Peschel U 2013 Phys. Rev. Lett. 110 223902
Google Scholar
[11] Yan Z Y, Wen Z C, Konotop V V 2015 Phys. Rev. A 92 023821
Google Scholar
[12] Yan Z Y, Wen Z C, Hang C 2015 Phys. Rev. E 92 022913
Google Scholar
[13] Yan Z Y 2013 Proc. R. Soc. London, Ser. A 371 20120059
Google Scholar
[14] Ablowitz M J, Musslimani Z H 2013 Phys. Rev. Lett. 110 064105
Google Scholar
[15] Lin M, Xu T 2015 Phys. Rev. E 91 033202
Google Scholar
[16] Xu T, Lan S, Li M, Zhang G W 2019 Physica D 390 47
Google Scholar
[17] Huang X, Ling L M 2016 Eur. Phys. J. Plus 131 148
Google Scholar
[18] Wen X Y, Yan Z Y, Yang Y Q 2016 Chaos 26 063123
Google Scholar
[19] Rao J G, He J S, Mihalache D, Cheng Y 2021 Z. Angew. Math. Phys. 72 1
Google Scholar
[20] Yang B, Yang J K 2019 Lett. Math. Phys. 109 945
Google Scholar
[21] Yang B, Yang J K 2020 J. Math. Anal. Appl. 487 124023
Google Scholar
[22] Yang B, Chen Y 2018 Chaos 28 053104
Google Scholar
[23] Rao J G, Cheng Y, Porsezian K, Mihalache D, He J S 2020 Physica D 401 132180
Google Scholar
[24] Rao J G, Zhang Y S, Fokas A S, He J S 2018 Nonlinearity 31 4090
Google Scholar
[25] Ablowitz M J, Musslimani Z H 2017 Stud. Appl. Math. 139 7
Google Scholar
[26] Lou S Y, Huang L 2017 Sci. Rep. 7 1
Google Scholar
[27] Lou S Y 2018 J. Math. Phys. 59 083507
Google Scholar
[28] Zhao Q, Jia M, Lou S Y 2019 Commun. Theor. Phys. 71 1149
Google Scholar
[29] Ablowitz M J, Musslimani Z H 2021 Phys. Lett. A 409 127516
Google Scholar
[30] Gürses M, Pekcan A 2022 Phys. Lett. A 422 127793
Google Scholar
[31] Liu S M, Wang J, Zhang D J 2022 Rep. Math. Phys. 89 199
Google Scholar
[32] Wang X, Wei J 2022 Appl. Math. Lett. 130 107998
Google Scholar
[33] Wang M M, Chen Y 2022 Nonlinear Dyn. 110 753
Google Scholar
[34] Yang J, Song H F, Fang M S, Ma L Y 2022 Nonlinear Dyn. 107 3767
Google Scholar
[35] Ren P, Rao J G 2022 Nonlinear Dyn. 108 2461
Google Scholar
[36] Wu J 2022 Nonlinear Dyn. 108 4021
Google Scholar
[37] Wei B, Liang J 2022 Nonlinear Dyn. 109 2969
Google Scholar
[38] Wang X B, Tian S F 2022 Theor. Math. Phys. 212 1193
Google Scholar
[39] Guo B L, Ling L L, Liu Q P 2012 Phys. Rev. E 85 026607
Google Scholar
[40] Ohta Y, Yang J K 2012 Proc. R. Soc. London, Ser. A 468 1716
Google Scholar
[41] He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914
Google Scholar
[42] Akhmediev N, Ankiewicz A, Soto-Crespo J M 2009 Phys. Rev. E 80 026601
Google Scholar
[43] Ling L M, Guo B L, Zhao L C 2014 Phys. Rev. E 89 041201
Google Scholar
[44] Zhao L C, Guo B L, Ling L L 2016 J. Math. Phys. 57 043508
Google Scholar
[45] Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S 2014 Phys. Rev. Lett. 113 034101
Google Scholar
[46] Chen S H, Mihalache D 2015 J. Phys. A: Math. Theor. 48 215202
Google Scholar
[47] Zhang G Q, Yan Z Y 2018 Commun. Nonlinear Sci. Numer. Simulat. 62 117
Google Scholar
[48] Bilman D, Miller P D 2019 Commun. Pure Appl. Math. 72 1722
Google Scholar
[49] Bilman D, Ling L M, Miller P D 2020 Duke Math. J. 169 671
Google Scholar
[50] Rao J G, Mihalache D, He J S 2022 Appl. Math. Lett. 134 108362
Google Scholar
[51] Rao J G, He J S, Malomed B A 2022 J. Math. Phys. 63 1
Google Scholar
[52] Rao J G, He J S, Cheng Y 2022 Lett. Math. Phys. 112 75
Google Scholar
[53] 郭柏灵, 田立新, 闫振亚, 凌黎明 2015 怪波及其数学理论 (浙江: 浙江科学技术出版社)
Guo B L, Tian L X, Tian Z Y, Ling L M 2015 Rogue Wave and Its Mathematical Theory (Zhejiang: Zhejiang Science and Technology Press)
[54] Peregrine D H 1983 J. Aust. Math. Soc. B 25 16
Google Scholar
[55] Hopkin M 2004 Nature 430 492
Google Scholar
[56] Muller P, Garret C, Osborne A 2005 Oceanography 18 66
Google Scholar
[57] Perkins S 2006 Science News 170 328
Google Scholar
[58] Kharif C, Pelinovsky E, Slunyaev A 2009 Rogue Waves in the Ocean (Heidelberg: Springer)
[59] Pelinovsky E, Kharif C 2008 Extreme Ocean Waves (Berlin: Springer)
[60] Solli D R, Ropers C, Koonath P, Jalali B 2007 Nature 450 06402
[61] Ganshin A N, Efimov V B, Kolmakov G V, Mezhov-Deglin L P, McClintock P 2008 Phys. Rev. Lett. 101 065303
Google Scholar
[62] Onorato M, Waseda T, Toffoli A, Cavaleri L, Gramstad O, Janssen P A E M, Kinoshita T, Monbaliu J, Mori N, Osborne A R, Serio M, Stansberg C T, Tamura H, Trulsen K 2009 Phys. Rev. Lett. 102 114502
Google Scholar
[63] Yang B, Yang J K 2021 Physica D 419 132850
Google Scholar
[64] Hirota R 2004 The Direct Method in Soliton Theory (Cambridge: Cambridge University Press)
[65] Jimbo M, Miwa T 1983 Publ. RIMS Kyoto Univ. 19 943
Google Scholar
[66] Date E, Kashiwara M, Jimbo M, Miwa T 1983 Transformation Groups for Soliton Equations, in Nonlinear Integrable Systems–Classical Theory and Quantum Theory (Singapore: World Scientific)
-
图 1 (a)非局域非线性薛定谔方程(2)的一阶怪波解(13), 参数取值为
$c_1^{ + } = {2}/{5},\; c_1^ - = {2}/{5},\; x_0 = 0$ ; (b)不同参数取值下一阶怪波解沿$ t = 0 $ 的截面图:$c_1^ + = c_1^ - = 0, \; x_0 = $ $ - 10$ (蓝色实线),$c_1^ + = c_1^ - = {1}/{5}, \; x_0 = 0$ (红色短虚线),$c_1^ + = c_1^ - = {2}/{5}, \; x_0 = 10$ (黑色长虚线)Figure 1. (a) The first-order rogue wave solutions (13) of the nonlocal NLS equation (2) with parameters
$c_1^{ + } = {2}/{5}, $ $ c_1^ - = {2}/{5},\; x_0 = 0$ ; (b) plot of the first-order rogue wave solutions along$ t = 0 $ with parameters$c_1^ + = c_1^ - = 0, $ $ x_0 = - 10$ (Blue solid line),$c_1^ + = c_1^ - = {1}/{5},\; x_0 = 0$ (Red short dotted line),$c_1^ + = c_1^ - = {2}/{5}, \; x_0 = 10$ (Black long dotted line).
图 2 (a)二阶怪波解的最大值
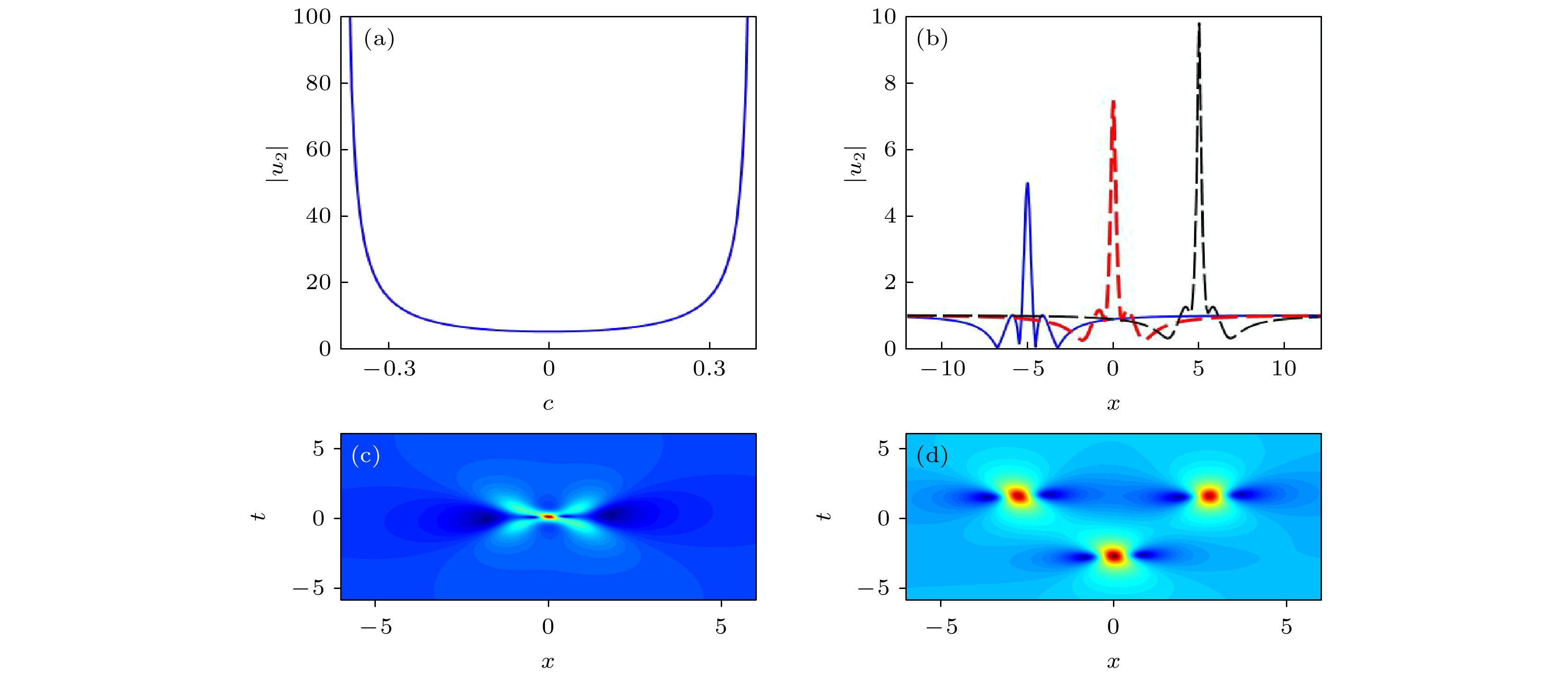
$ |u_2(x_0, 0)| $ 随$ c_1^{ + } = c_1^{ - } $ 变化; (b)不同参数取值下一阶怪波解沿$ t = 0 $ 的截面图:$c_1^ + = c_1^ - = $ $ 0, \;x_0 = - 10$ (蓝色实线),$c_1^ + = c_1^ - = {1}/{5},\; x_0 = 0$ (红色短虚线),$c_1^ + = c_1^ - = {1}/{4}, \;x_0 = 10$ (黑色长虚线); (c)二阶怪波解$ |u_2 | $ 的基本模式, 参数$c_1^{ + } = c_1^{ - } = {1}/{10}, \;c_3^{ + } = c_3^{ - } = 0$ ; (d)二阶怪波解$ |u_2 | $ 的三角模式, 参数$c_1^{ + } = c_1^{ - } = {1}/{10},\; c_3^{ + } = - c_3^{ - } = 10$ Figure 2. (a) Changes in the maximum of the second-order rogue wave
$ |u_2(x_0, 0)| $ along$ c_1^{ + } = c_1^{ - } $ ; (b) pot of the second-order rogue waves along$ t = 0 $ with different parameters:$c_1^ + = c_1^ - = 0, \;x_0 = - 10$ (Blue solid line),$c_1^ + = c_1^ - = {1}/{5},\;x_0 = 0$ (Red short dotted line),$c_1^ + = c_1^ - = {1}/{4},\; x_0 = 10$ (Black long dotted line); (c) fundamental pattern of the second-order rogue wave solution$ |u_2 | $ with parameters$c_1^{ + } = c_1^{ - }= {1}/{10},\; c_3^{ + } = c_3^{ - } = 0$ ; (d) triangle pattern of the second-order rogue wave solution$ |u_2 | $ with parameters$c_1^{ + } = c_1^{ - } = {1}/{10}, \;c_3^{ + } = - c_3^{ - } = 10$ 
图 3 从左往右四列依次为3阶至6阶怪波在不同参数下的模式, 所有图形中参数
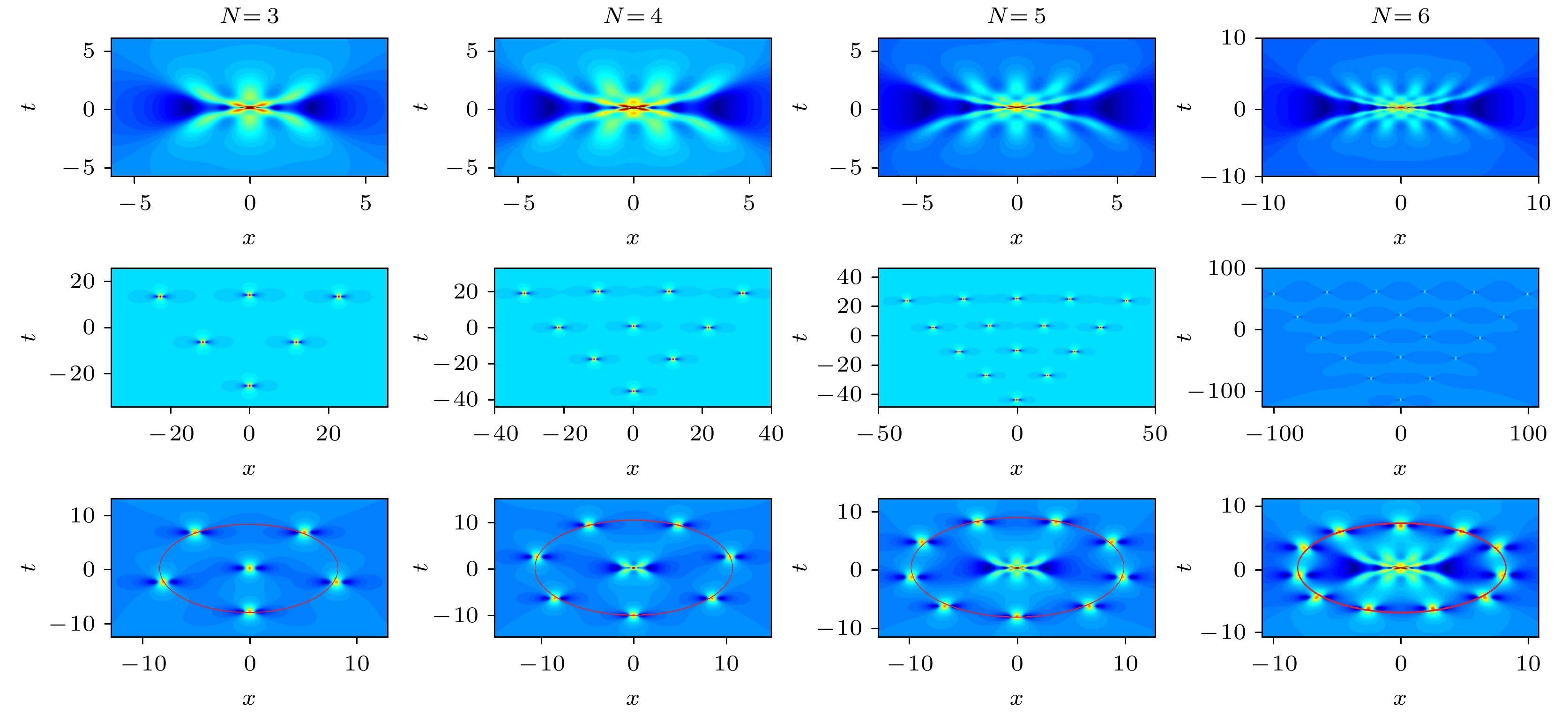
$c_1^{\pm} = ({1}/{100}){\rm{i}}$ . 第一行: 3阶至6阶怪波的基本模式,$ c_{2 j-1}^{\pm} = 0 $ ; 第二行: 3阶至6阶怪波的三角模式,$ c_{3}^{\pm} = \pm10^{N - 2} $ (从左往右图形中N的值依次为$ 3, 4, 5, 6 $ ), 其他参数均为0; 第三行: 3阶至6阶怪波的圆形模式,$ c_{2 N - 1}^{\pm} = \pm10000 $ (从左往右图形中N的值依次为$ 3, 4, 5, 6 $ ), 其他参数均为0Figure 3. The four columns from left to right correspond to the patterns of third-order to sixth-order rogue waves with
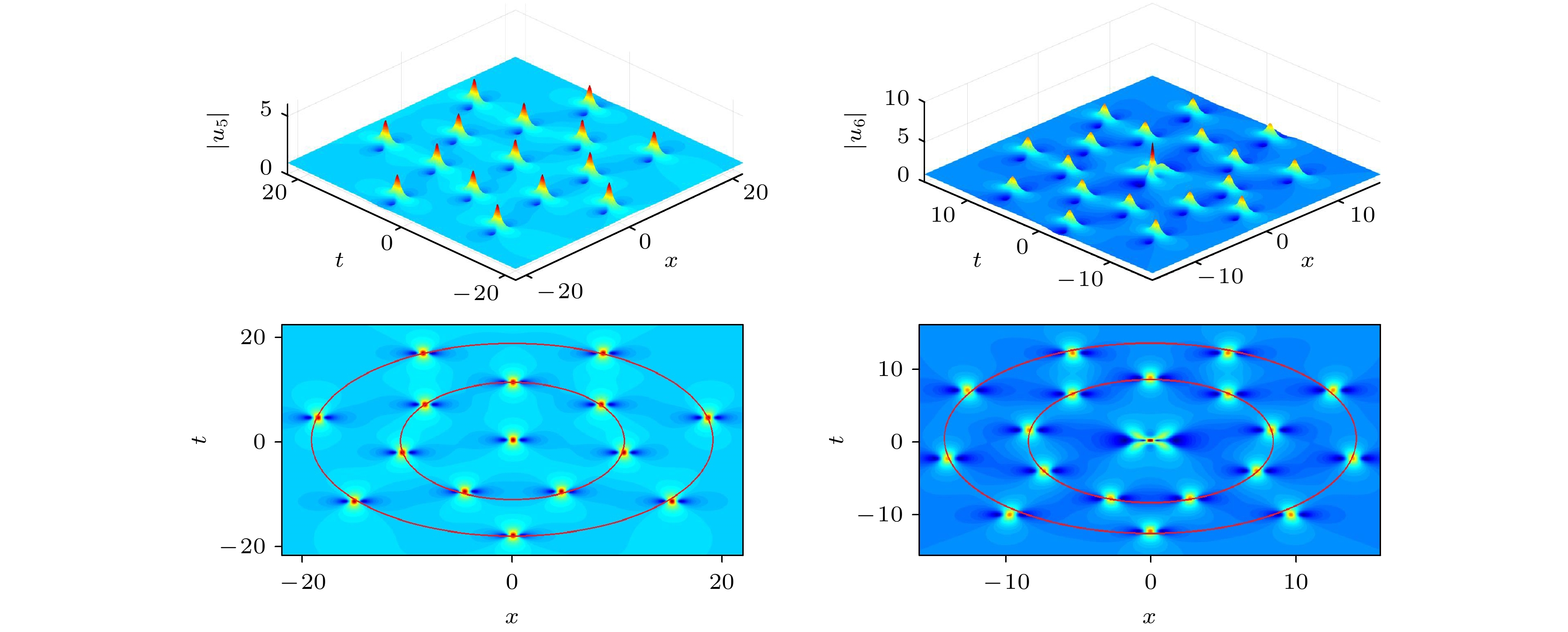
$c_1^{\pm} = ({1}/{100}){\rm{i}}$ and different parameters: The first row: The fundamental patterns of third-order to sixth-order rogue waves with parameters$ c_{2 j - 1}^{\pm} = 0 $ ; The second row: The triangle patterns of third-order to sixth-order rogue waves with parameters$ c_{3}^{\pm} = \pm10^{N - 2} $ (The value of N in the figures from left to right is$ 3, 4, 5, 6 $ ), and the other parameters are zero; The third row: The circular patterns of third-order to sixth-order rogue waves with parameters$ c_{2 N-1}^{\pm} = \pm10000 $ (The value of N in the figures from left to right is$ 3, 4, 5, 6 $ ), and the other parameters are zero
图 4 左列为5阶怪波的双环形模式, 参数取值为
$ c_7^{\pm} = \pm10000 $ , 其他参数为0. 右列为6阶怪波的双环形模式, 参数取值为$ c_9^{\pm} = \pm10000 $ , 其他参数为0Figure 4. The left column is double ring pattern of the fifth-order rogue wave with parameters
$ c_7^{\pm} = \pm10000 $ and the other parameter being zero. The right column is double ring pattern of the sixth-order rogue wave with parameters$ c_9^{\pm} = \pm10000 $ and the other parameters being zero -
[1] Ablowitz M J, Segur H 1981 Solitons and Inverse Scattering Transform (Philadelphia: SIAM)
[2] Yang J K 2010 Nonlinear Waves in Integrable and Nonintegrable Systems (Philadelphia: SIAM)
[3] Bender C M, Boettcher S 1988 Phys. Rev. Lett. 80 5243
Google Scholar
[4] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201
Google Scholar
[5] Mostafazadeh A 2003 J. Phys. A: Math. Gen. 36 7081
Google Scholar
[6] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
Google Scholar
[7] Regensburger A, Bersch C, Miri M A, Onishchukov G, Christodoulides D N, Peschel U 2012 Nature 488 167
Google Scholar
[8] Makris K G, El-Ganainy R, Christodoulides D N, Musslimani Z H 2008 Phys. Rev. Lett. 100 103904
Google Scholar
[9] Ruter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192
Google Scholar
[10] Regensburger A, Miri M A, Bersch C, Nager J, Onishchukov G, Christodoulides D N, Peschel U 2013 Phys. Rev. Lett. 110 223902
Google Scholar
[11] Yan Z Y, Wen Z C, Konotop V V 2015 Phys. Rev. A 92 023821
Google Scholar
[12] Yan Z Y, Wen Z C, Hang C 2015 Phys. Rev. E 92 022913
Google Scholar
[13] Yan Z Y 2013 Proc. R. Soc. London, Ser. A 371 20120059
Google Scholar
[14] Ablowitz M J, Musslimani Z H 2013 Phys. Rev. Lett. 110 064105
Google Scholar
[15] Lin M, Xu T 2015 Phys. Rev. E 91 033202
Google Scholar
[16] Xu T, Lan S, Li M, Zhang G W 2019 Physica D 390 47
Google Scholar
[17] Huang X, Ling L M 2016 Eur. Phys. J. Plus 131 148
Google Scholar
[18] Wen X Y, Yan Z Y, Yang Y Q 2016 Chaos 26 063123
Google Scholar
[19] Rao J G, He J S, Mihalache D, Cheng Y 2021 Z. Angew. Math. Phys. 72 1
Google Scholar
[20] Yang B, Yang J K 2019 Lett. Math. Phys. 109 945
Google Scholar
[21] Yang B, Yang J K 2020 J. Math. Anal. Appl. 487 124023
Google Scholar
[22] Yang B, Chen Y 2018 Chaos 28 053104
Google Scholar
[23] Rao J G, Cheng Y, Porsezian K, Mihalache D, He J S 2020 Physica D 401 132180
Google Scholar
[24] Rao J G, Zhang Y S, Fokas A S, He J S 2018 Nonlinearity 31 4090
Google Scholar
[25] Ablowitz M J, Musslimani Z H 2017 Stud. Appl. Math. 139 7
Google Scholar
[26] Lou S Y, Huang L 2017 Sci. Rep. 7 1
Google Scholar
[27] Lou S Y 2018 J. Math. Phys. 59 083507
Google Scholar
[28] Zhao Q, Jia M, Lou S Y 2019 Commun. Theor. Phys. 71 1149
Google Scholar
[29] Ablowitz M J, Musslimani Z H 2021 Phys. Lett. A 409 127516
Google Scholar
[30] Gürses M, Pekcan A 2022 Phys. Lett. A 422 127793
Google Scholar
[31] Liu S M, Wang J, Zhang D J 2022 Rep. Math. Phys. 89 199
Google Scholar
[32] Wang X, Wei J 2022 Appl. Math. Lett. 130 107998
Google Scholar
[33] Wang M M, Chen Y 2022 Nonlinear Dyn. 110 753
Google Scholar
[34] Yang J, Song H F, Fang M S, Ma L Y 2022 Nonlinear Dyn. 107 3767
Google Scholar
[35] Ren P, Rao J G 2022 Nonlinear Dyn. 108 2461
Google Scholar
[36] Wu J 2022 Nonlinear Dyn. 108 4021
Google Scholar
[37] Wei B, Liang J 2022 Nonlinear Dyn. 109 2969
Google Scholar
[38] Wang X B, Tian S F 2022 Theor. Math. Phys. 212 1193
Google Scholar
[39] Guo B L, Ling L L, Liu Q P 2012 Phys. Rev. E 85 026607
Google Scholar
[40] Ohta Y, Yang J K 2012 Proc. R. Soc. London, Ser. A 468 1716
Google Scholar
[41] He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914
Google Scholar
[42] Akhmediev N, Ankiewicz A, Soto-Crespo J M 2009 Phys. Rev. E 80 026601
Google Scholar
[43] Ling L M, Guo B L, Zhao L C 2014 Phys. Rev. E 89 041201
Google Scholar
[44] Zhao L C, Guo B L, Ling L L 2016 J. Math. Phys. 57 043508
Google Scholar
[45] Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S 2014 Phys. Rev. Lett. 113 034101
Google Scholar
[46] Chen S H, Mihalache D 2015 J. Phys. A: Math. Theor. 48 215202
Google Scholar
[47] Zhang G Q, Yan Z Y 2018 Commun. Nonlinear Sci. Numer. Simulat. 62 117
Google Scholar
[48] Bilman D, Miller P D 2019 Commun. Pure Appl. Math. 72 1722
Google Scholar
[49] Bilman D, Ling L M, Miller P D 2020 Duke Math. J. 169 671
Google Scholar
[50] Rao J G, Mihalache D, He J S 2022 Appl. Math. Lett. 134 108362
Google Scholar
[51] Rao J G, He J S, Malomed B A 2022 J. Math. Phys. 63 1
Google Scholar
[52] Rao J G, He J S, Cheng Y 2022 Lett. Math. Phys. 112 75
Google Scholar
[53] 郭柏灵, 田立新, 闫振亚, 凌黎明 2015 怪波及其数学理论 (浙江: 浙江科学技术出版社)
Guo B L, Tian L X, Tian Z Y, Ling L M 2015 Rogue Wave and Its Mathematical Theory (Zhejiang: Zhejiang Science and Technology Press)
[54] Peregrine D H 1983 J. Aust. Math. Soc. B 25 16
Google Scholar
[55] Hopkin M 2004 Nature 430 492
Google Scholar
[56] Muller P, Garret C, Osborne A 2005 Oceanography 18 66
Google Scholar
[57] Perkins S 2006 Science News 170 328
Google Scholar
[58] Kharif C, Pelinovsky E, Slunyaev A 2009 Rogue Waves in the Ocean (Heidelberg: Springer)
[59] Pelinovsky E, Kharif C 2008 Extreme Ocean Waves (Berlin: Springer)
[60] Solli D R, Ropers C, Koonath P, Jalali B 2007 Nature 450 06402
[61] Ganshin A N, Efimov V B, Kolmakov G V, Mezhov-Deglin L P, McClintock P 2008 Phys. Rev. Lett. 101 065303
Google Scholar
[62] Onorato M, Waseda T, Toffoli A, Cavaleri L, Gramstad O, Janssen P A E M, Kinoshita T, Monbaliu J, Mori N, Osborne A R, Serio M, Stansberg C T, Tamura H, Trulsen K 2009 Phys. Rev. Lett. 102 114502
Google Scholar
[63] Yang B, Yang J K 2021 Physica D 419 132850
Google Scholar
[64] Hirota R 2004 The Direct Method in Soliton Theory (Cambridge: Cambridge University Press)
[65] Jimbo M, Miwa T 1983 Publ. RIMS Kyoto Univ. 19 943
Google Scholar
[66] Date E, Kashiwara M, Jimbo M, Miwa T 1983 Transformation Groups for Soliton Equations, in Nonlinear Integrable Systems–Classical Theory and Quantum Theory (Singapore: World Scientific)
DownLoad:
Catalog
Metrics
- Abstract views: 3233
- PDF Downloads: 132
- Cited By: 0
