-
本文构造了一类高阶Ablowitz-Ladik方程的广义
$(M, N-M)$ -波Darboux变换, 借助符号计算从不同背景出发研究了该模型丰富的局域波解, 并利用数值模拟研究了这些解的动力学稳定性.-
关键词:
- 高阶Ablowitz-Ladik方程 /
- 广义(M, N-M)-波Darboux变换 /
- 局域波 /
- 怪波
It is an important research topic to study diverse local wave interaction phenomena in nonlinear evolution equations, especially for the semi-discrete nonlinear lattice equations, there is little work on their diverse local wave interaction solutions due to the complexity and difficulty of research. In this paper, a semi-discrete higher-order Ablowitz-Ladik equation is investigated via the generalized$(M, N-M)$ -fold Darboux transformation. With the aid of symbolic computation, diverse types of localized wave solutions are obtained starting from constant and plane wave seed background. Particularly, for the case$M=N$ , the generalized$(M, N-M)$ -fold Darboux transformation may reduce to the N-fold Darboux transformation which can be used to derive multi-soliton solutions from constant seed background and breather solutions from plane wave seed background, respectively. For the case$M=1$ , the generalized$(M, N-M)$ -fold Darboux transformation reduce to the generalized$(1, N-1)$ -fold one which can be used to obtain rogue wave solutions from plane wave seed background. For the case$M=2$ , the generalized$(M, N-M)$ -fold Darboux transformation reduce to the generalized$(2, N-2)$ -fold one which can be used to give mixed interaction solutions of one-breather and first-order rogue wave from plane wave seed background. To study the propagation characteristics of such localized waves, the numerical simulations are used to explore the dynamical stability of such obtained solutions. Results obtained in the present work may be used to explain related physical phenomena in nonlinear optics and relevant fields.-
Keywords:
- higher-order Ablowitz-Ladik equation /
- generalized (M, N-M)-fold Darboux transformation /
- localized wave /
- rogue wave
[1] 尤福财 2008 博士学位论文 (上海: 上海大学)
You F C 2008 Ph. D. Dissertation (Shanghai: Shanghai University) (in Chinese)
[2] Toda M 1967 J. Phys. Soc. Jpn. 23 501
Google Scholar
[3] 李翊神 1999 孤子与可积系统 (上海: 上海科技教育出版社) 第25页
Li Y S 1999 Soliton and Integrable System (Shanghai: Shanghai Scientific and Technological Education Publishing House) p25 (in Chinese)
[4] 広田良吾 著 (王红艳, 李春霞, 赵俊霄, 虞国富 译) 2004 孤子理论中的直接方法(北京: 清华大学出版社) 第59页
Hirota R (translated by Wang H Y, Li C X, Zhao J X, Yu G F) 2004 The Direct Method in Soliton Theory (New York: Cambridge University Press) p59
[5] Yue Y F, Huang L L, Chen Y 2018 Comput. Math. Appl. 75 2538
Google Scholar
[6] Huang L L, Yue Y F, Chen Y 2018 Comput. Math. Appl. 74 831
[7] Liu C, Yang Z Y, Yang W L, Akhmediev N 2019 J. Opt. Soc. Am. B 36 1294
Google Scholar
[8] Ren Y, Wang X, Liu C, Yang Z Y, Yang W L 2018 Commun. Nonlinear Sci. Numer. Simul. 63 161
Google Scholar
[9] Liu C, Ren Y, Yang Z Y, Yang W L 2017 Chaos 27 083120
Google Scholar
[10] Liu C, Yang Z Y, Yang W L 2017 Chaos 28 083110
[11] Ren Y, Liu C, Yang Z Y, Yang W L 2018 Phys. Rev. E 98 062223
Google Scholar
[12] Li H, Lou S Y 2019 Chin. Phys. Lett. 36 050501
Google Scholar
[13] Zhao L C, Yang Z Y, Yang W L 2019 Chin. Phys. B 28 010501
Google Scholar
[14] Liu X S, Zhao L C, Duan L, Peng G, Yang Z Y, Yang W L 2018 Chin. Phys. Lett. 35 020501
Google Scholar
[15] 李淑青, 杨光晔, 李禄 2014 63 104215
Google Scholar
Li S Q, Yang G Y, Li L 2014 Acta Phys. Sin. 63 104215
Google Scholar
[16] 孙俊超, 张宗国, 董焕河, 杨红卫 2014 21 210201
Google Scholar
Sun J C, Zhang Z G, Dong H H, Yang H W 2014 Acta Phys. Sin. 21 210201
Google Scholar
[17] Wen X Y, Yan Z Y 2015 Chaos 25 123115
Google Scholar
[18] Wen X Y, Yang Y Q, Yan Z Y 2015 Phys. Rev. E 92 012917
Google Scholar
[19] Wen X Y, Yan Z Y, Yang Y Q 2016 Chaos 26 063123
Google Scholar
[20] Wen X Y, Yan Z Y 2017 Commun. Nonlinear Sci. Numer. Simul. 43 311
Google Scholar
[21] Wang H T, Wen X Y, Wang D S 2019 Wave Motion 91 102396
Google Scholar
[22] Huang L L, Qiao Z J, Chen Y 2018 Chin. Phys. B 27 020201
Google Scholar
[23] Zhang G, Yan Z Y, Wen X Y, Chen Y 2017 Phys. Rev. E 95 042201
Google Scholar
[24] Zhang G, Yan Z Y, Wen X Y 2018 Physica D 366 27
Google Scholar
[25] Yang J, Zhu Z N 2018 Chin. Phys. Lett. 35 090201
Google Scholar
[26] Wen X Y, Yan Z, Malomed B A 2016 Chaos 26 123110
Google Scholar
[27] Ablowitz M J, Clarkson P A 1991 Soliton, Nonlinear Evolution Equations and Inverse Scattering (New York: Cambridge University Press) p55
[28] Ankiewicz A, Akhmediev N, Soto-Crespo J M 2010 Phys. Rev. E 82 026602
Google Scholar
[29] Ankiewicz A, Akhmediev N, Lederer F 2011 Phys. Rev. E 83 056602
Google Scholar
[30] Ohta Y, Yang J 2014 J. Phys. A: Math. Theor. 47 255201
Google Scholar
[31] Lee L, Lyng G, Vankova I 2012 Physica D 241 1767
Google Scholar
-
图 1 (a1)−(c1)取参数
$ \lambda_1 = -1+2 {\rm i} $ 时的一孤子解; (a2)−(c2)取参数$ \lambda_1 = 3+{\rm i}, \lambda_2 = 1+2 {\rm i} $ 时的二孤子解. 左列: 精确解; 中列: 数值解; 右列: 加$ 2\% $ 小噪声的数值解. 圈中的数字1和2分别表示参数$ \lambda_1 $ 和$ \lambda_2 $ 对应的孤子Fig. 1. (a1)−(c1) One-soliton solution with parameter
$ \lambda_1 = -1+2 {\rm i} $ ; (a2)−(c2) two-soliton solution with parameters$ \lambda_1 = 3+{\rm i}, \lambda_2 = 1+2 {\rm i} $ . Left column: Exact solutions; Middle column: Numerical solutions without noise; Right column: Numerical solutions with$ 2\% $ small noise.
图 2 (a1)−(c1)取参数
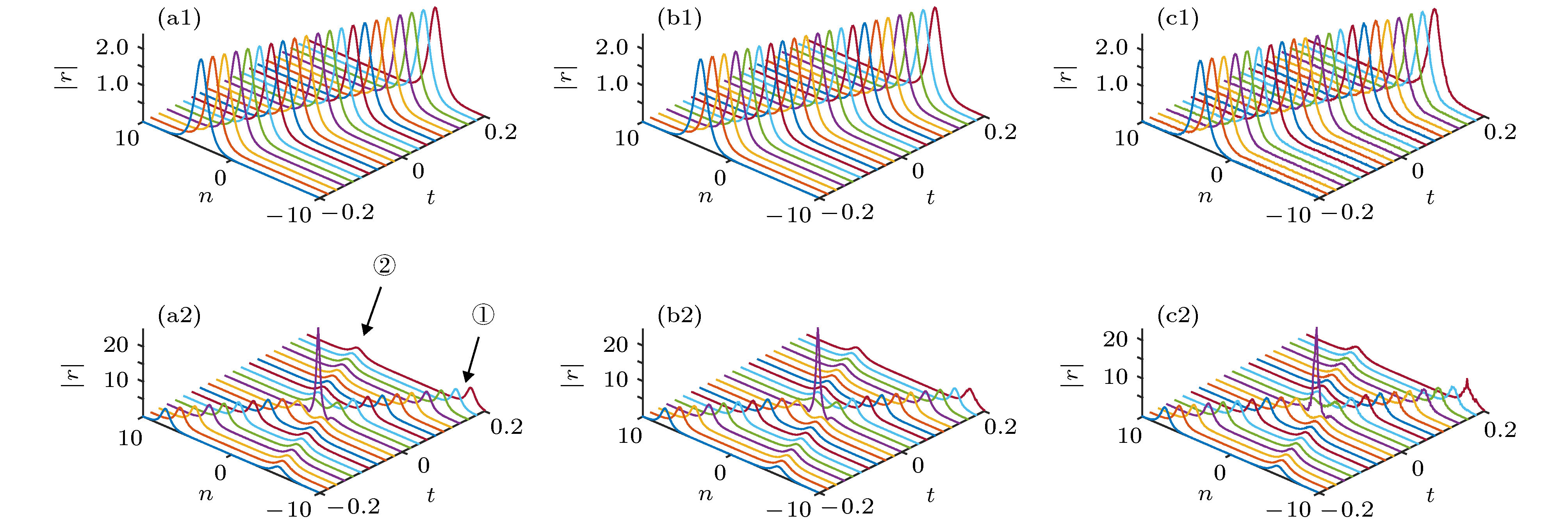
$ \lambda_1 ={11}/{4} $ 时的一呼吸子解; (a2)−(c2)取参数$ \lambda_1 = 2, \lambda_2 = 3 $ 时的二呼吸子解. 左列: 精确解; 中列: 数值解; 右列: 加$ 2\% $ 小噪声的数值解. 圈中的数字1和2分别表示参数$ \lambda_1 $ 和$ \lambda_2 $ 对应的呼吸子Fig. 2. (a1)−(c1) One-breather solution with parameter
$ \lambda_1 ={11}/{4} $ ; (a2)−(c2) two-breather solution with parameters$ \lambda_1 = 2, \lambda_2 = 3 $ . Left column: Exact solutions; Middle column: Numerical solutions without noise; Right column: Numerical solutions with$ 2\% $ small noise.
图 3 (a1)—(c1)一阶怪波解; (a2)—(c2)取参数
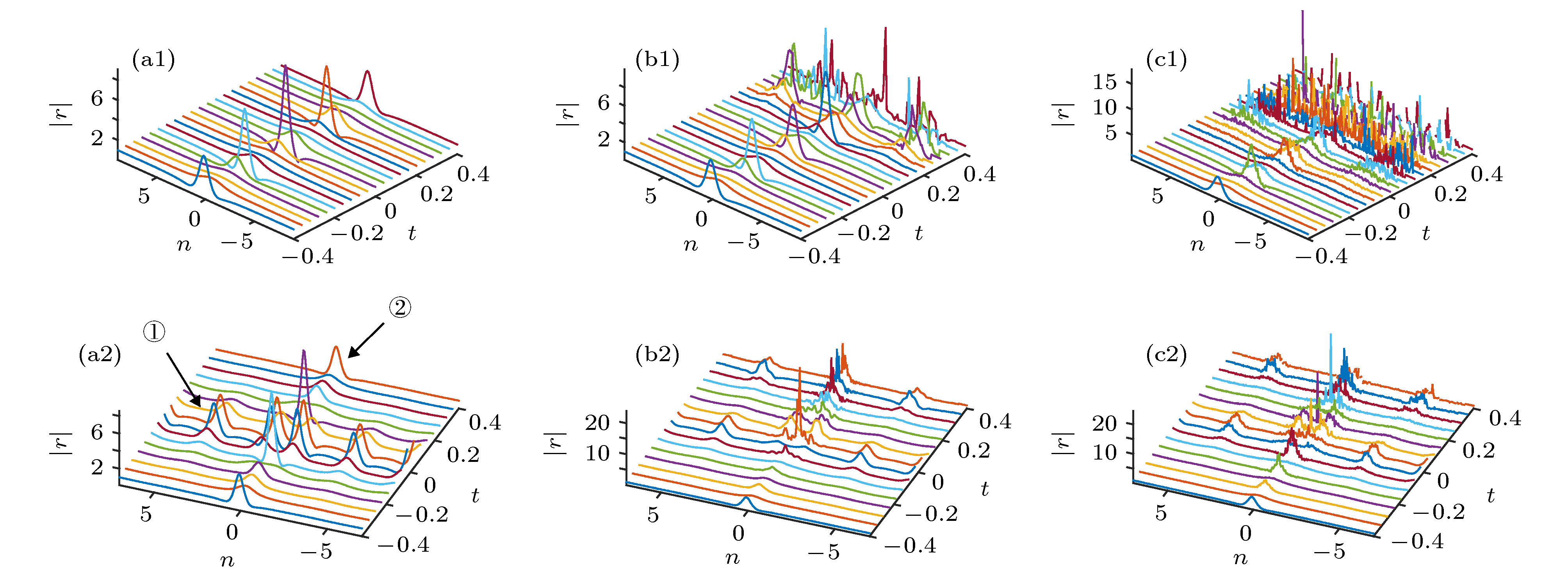
$ e_1 = d_1 = 0 $ 时具有强作用的二阶怪波解; (a3)—(c3)取参数$ e_1 = 100, d_1 = 0 $ 时具有弱作用的二阶怪波解. 左列: 精确解; 中列: 数值解; 右列: 加$ 2\% $ 小噪声的数值解Fig. 3. (a1)−(c1) First-order rogue wave solution; (a2)−(c2) strong interaction second-order rogue wave solution with
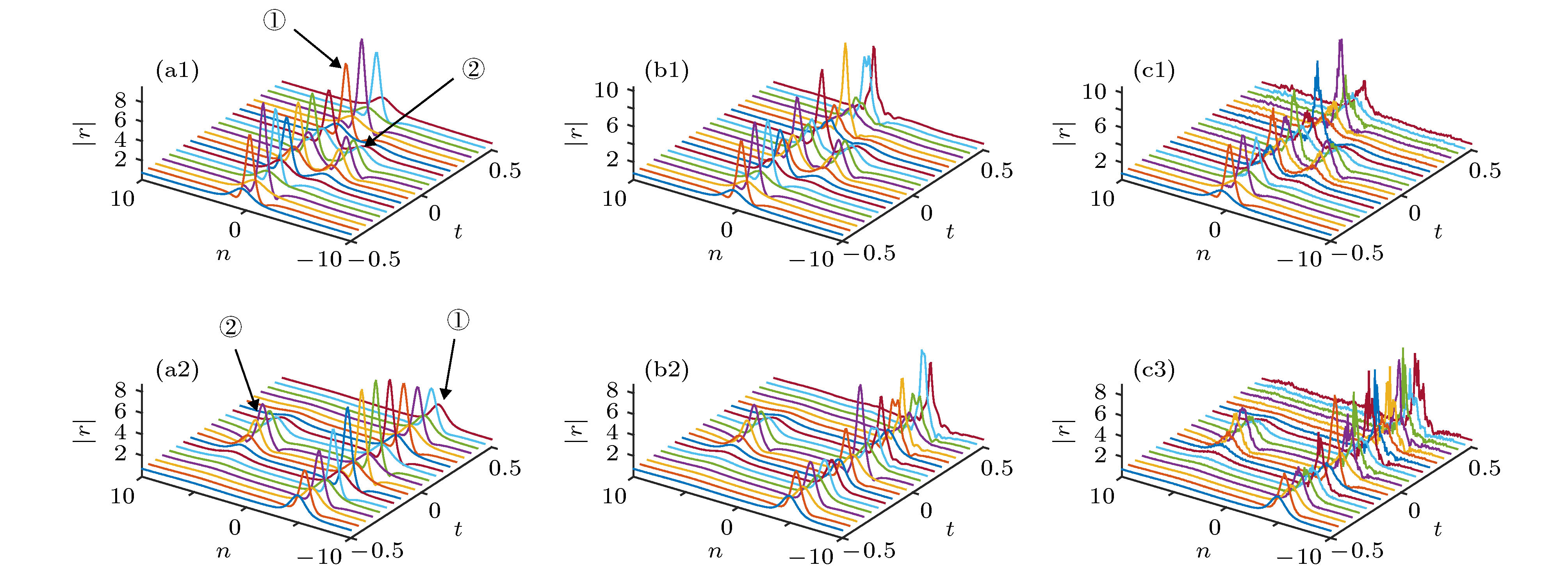
$ e_1 = d_1 = 0 $ ; (a3)−(c3) weak interaction second-order rogue wave solution with$ e_1 = 100, d_1 = 0 $ . Left column: Exact solutions; Middle column: Numerical solutions without noise; Right column: Numerical solutions with$ 2\% $ small noise.
图 4 (a1)—(c1)一呼吸子和一阶怪波的混合强作用; (a2)—(c2)一呼吸子和一阶怪波的混合弱作用. 左列: 精确解; 中列: 数值解; 右列: 加
$ 2\% $ 小噪声的数值解. 圈中的数字1表示呼吸子, 数字2表示怪波Fig. 4. (a1)−(c1) Mixed strong interaction between one-breather and first-order rogue wave; (a2)−(c2) mixed weak interaction between one-breather and first-order rogue wave. Left column: Exact solutions; Middle column: Numerical solutions without noise; Right column: Numerical solutions with
$ 2\% $ small noise. -
[1] 尤福财 2008 博士学位论文 (上海: 上海大学)
You F C 2008 Ph. D. Dissertation (Shanghai: Shanghai University) (in Chinese)
[2] Toda M 1967 J. Phys. Soc. Jpn. 23 501
Google Scholar
[3] 李翊神 1999 孤子与可积系统 (上海: 上海科技教育出版社) 第25页
Li Y S 1999 Soliton and Integrable System (Shanghai: Shanghai Scientific and Technological Education Publishing House) p25 (in Chinese)
[4] 広田良吾 著 (王红艳, 李春霞, 赵俊霄, 虞国富 译) 2004 孤子理论中的直接方法(北京: 清华大学出版社) 第59页
Hirota R (translated by Wang H Y, Li C X, Zhao J X, Yu G F) 2004 The Direct Method in Soliton Theory (New York: Cambridge University Press) p59
[5] Yue Y F, Huang L L, Chen Y 2018 Comput. Math. Appl. 75 2538
Google Scholar
[6] Huang L L, Yue Y F, Chen Y 2018 Comput. Math. Appl. 74 831
[7] Liu C, Yang Z Y, Yang W L, Akhmediev N 2019 J. Opt. Soc. Am. B 36 1294
Google Scholar
[8] Ren Y, Wang X, Liu C, Yang Z Y, Yang W L 2018 Commun. Nonlinear Sci. Numer. Simul. 63 161
Google Scholar
[9] Liu C, Ren Y, Yang Z Y, Yang W L 2017 Chaos 27 083120
Google Scholar
[10] Liu C, Yang Z Y, Yang W L 2017 Chaos 28 083110
[11] Ren Y, Liu C, Yang Z Y, Yang W L 2018 Phys. Rev. E 98 062223
Google Scholar
[12] Li H, Lou S Y 2019 Chin. Phys. Lett. 36 050501
Google Scholar
[13] Zhao L C, Yang Z Y, Yang W L 2019 Chin. Phys. B 28 010501
Google Scholar
[14] Liu X S, Zhao L C, Duan L, Peng G, Yang Z Y, Yang W L 2018 Chin. Phys. Lett. 35 020501
Google Scholar
[15] 李淑青, 杨光晔, 李禄 2014 63 104215
Google Scholar
Li S Q, Yang G Y, Li L 2014 Acta Phys. Sin. 63 104215
Google Scholar
[16] 孙俊超, 张宗国, 董焕河, 杨红卫 2014 21 210201
Google Scholar
Sun J C, Zhang Z G, Dong H H, Yang H W 2014 Acta Phys. Sin. 21 210201
Google Scholar
[17] Wen X Y, Yan Z Y 2015 Chaos 25 123115
Google Scholar
[18] Wen X Y, Yang Y Q, Yan Z Y 2015 Phys. Rev. E 92 012917
Google Scholar
[19] Wen X Y, Yan Z Y, Yang Y Q 2016 Chaos 26 063123
Google Scholar
[20] Wen X Y, Yan Z Y 2017 Commun. Nonlinear Sci. Numer. Simul. 43 311
Google Scholar
[21] Wang H T, Wen X Y, Wang D S 2019 Wave Motion 91 102396
Google Scholar
[22] Huang L L, Qiao Z J, Chen Y 2018 Chin. Phys. B 27 020201
Google Scholar
[23] Zhang G, Yan Z Y, Wen X Y, Chen Y 2017 Phys. Rev. E 95 042201
Google Scholar
[24] Zhang G, Yan Z Y, Wen X Y 2018 Physica D 366 27
Google Scholar
[25] Yang J, Zhu Z N 2018 Chin. Phys. Lett. 35 090201
Google Scholar
[26] Wen X Y, Yan Z, Malomed B A 2016 Chaos 26 123110
Google Scholar
[27] Ablowitz M J, Clarkson P A 1991 Soliton, Nonlinear Evolution Equations and Inverse Scattering (New York: Cambridge University Press) p55
[28] Ankiewicz A, Akhmediev N, Soto-Crespo J M 2010 Phys. Rev. E 82 026602
Google Scholar
[29] Ankiewicz A, Akhmediev N, Lederer F 2011 Phys. Rev. E 83 056602
Google Scholar
[30] Ohta Y, Yang J 2014 J. Phys. A: Math. Theor. 47 255201
Google Scholar
[31] Lee L, Lyng G, Vankova I 2012 Physica D 241 1767
Google Scholar
-
[1] 饶继光, 陈生安, 吴昭君, 贺劲松. 空间位移 $\mathcal{PT}$ 对称非局域非线性薛定谔方程的高阶怪波解. , 2023, 72(10): 104204. doi: 10.7498/aps.72.20222298[2] 张解放, 俞定国, 金美贞. (2+1)维Zakharov方程的自相似变换和线怪波簇激发. , 2022, 71(8): 084204. doi: 10.7498/aps.71.20211181 [3] 张解放, 俞定国, 金美贞. 二维自相似变换理论和线怪波激发. , 2022, 71(1): 014205. doi: 10.7498/aps.71.20211417 [4] 王艳, 李禄. 基于怪波实现光脉冲串的全光放大. , 2021, 70(22): 224213. doi: 10.7498/aps.70.20210959 [5] 李再东, 郭奇奇. 铁磁纳米线中磁化强度的磁怪波. , 2020, 69(1): 017501. doi: 10.7498/aps.69.20191352 [6] 张解放, 金美贞, 胡文成. 非自治Kadomtsev-Petviashvili方程的自相似变换和二维怪波构造. , 2020, 69(24): 244205. doi: 10.7498/aps.69.20200981 [7] 陈智敏, 段文山. 弹性管中的怪波. , 2020, 69(1): 014701. doi: 10.7498/aps.69.20191308 [8] 张解放, 金美贞. Fokas系统的怪波激发. , 2020, 69(21): 214203. doi: 10.7498/aps.69.20200710 [9] 李敏, 王博婷, 许韬, 水涓涓. 四阶色散非线性薛定谔方程的明暗孤立波和怪波的形成机制. , 2020, 69(1): 010502. doi: 10.7498/aps.69.20191384 [10] 吴丹丹, 佘卫龙. 线性吸收介质非局域线性电光效应的耦合波理论. , 2017, 66(6): 064202. doi: 10.7498/aps.66.064202 [11] 李凯辉, 刘汉泽, 辛祥鹏. 一类高阶非线性波方程的李群分析、最优系统、精确解和守恒律. , 2016, 65(14): 140201. doi: 10.7498/aps.65.140201 [12] 朱席席, 肖勇, 温激鸿, 郁殿龙. 局域共振型加筋板的弯曲波带隙与减振特性. , 2016, 65(17): 176202. doi: 10.7498/aps.65.176202 [13] 张文玲, 马松华, 陈晶晶. (2+1)维Korteweg-de Vries方程的复合波解及局域激发. , 2014, 63(8): 080506. doi: 10.7498/aps.63.080506 [14] 李淑青, 杨光晔, 李禄. Hirota方程的怪波解及其传输特性研究. , 2014, 63(10): 104215. doi: 10.7498/aps.63.104215 [15] 丁锐, 金亚秋, 小仓久直. 二维随机介质中柱面波传播及其局域性的随机泛函分析. , 2010, 59(6): 3674-3685. doi: 10.7498/aps.59.3674 [16] 钟敏, 唐国宁. 局域反馈抑制心脏中的螺旋波和时空混沌. , 2010, 59(3): 1593-1599. doi: 10.7498/aps.59.1593 [17] 丁 锐, 王志良, 小仓久直. 二维各向同性均匀随机介质中平面波的传播及其局域性. , 2008, 57(9): 5519-5528. doi: 10.7498/aps.57.5519 [18] 赵熙强, 唐登斌, 王利民, 张耀明. 高阶(2+1)维Broer-Kaup方程的孤波解. , 2003, 52(8): 1827-1831. doi: 10.7498/aps.52.1827 [19] 郭儒, 刘思敏, 凌振芳, 门丽秋, 孙骞, 张光寅. 在局域响应的LiNbO3:Fe晶体的多波混合. , 1994, 43(12): 1973-1978. doi: 10.7498/aps.43.1973 [20] 李荫远, 朱砚磬. 立方铁磁体中的自旋波局域模. , 1963, 19(11): 753-763. doi: 10.7498/aps.19.753
下载:
计量
- 文章访问数: 7828
- PDF下载量: 179
- 被引次数: 0
