非自治Kadomtsev-Petviashvili方程的自相似变换和二维怪波构造

张解放; 金美贞; 胡文成

doi:10.7498/aps.69.20200981

摘要

首先给出非自治Kadomtsev-Petviashvili方程转换为Kadomtsev- Petviashvili方程的一个自相似变换, 然后基于Kadomtsev-Petviashvili方程的Lump解构造了非自治Kadomtsev-Petviashvili方程的有理函数表示的二维单、双、三怪波解, 最后通过合适选取变参数, 用图示说明了它们的演化特征, 并利用快速傅里叶变换算法数值模拟测试了二维单怪波的动力学稳定性. 本文方法对寻找(2 + 1)维非线性波动模型的怪波激发提供了启迪.

关键词:

Abstract

Rogue wave is a kind of natural phenomenon that is fascinating, rare, and extreme. It has become a frontier of academic research. The rogue wave is considered as a spatiotemporal local rational function solution of nonlinear wave model. There are still very few (2 + 1)-dimensional nonlinear wave models which have rogue wave solutions, in comparison with soliton and Lump waves that are found in almost all (2 + 1)-dimensional nonlinear wave models and can be solved by different methods, such as inverse scattering method, Hirota bilinear method, Darboux transform method, Riemann-Hilbert method, and homoclinic test method. The structure and evolution characteristics of the obtained (2 + 1)-dimensional rogue waves are quite different from the prototypes of the (1 + 1)-dimensional nonlinear Schrödinger equation. Therefore, it is of great value to study two-dimensional rogue waves.In this paper, the non-autonomous Kadomtsev-Petviashvili equation is first converted into the Kadomtsev-Petviashvili equation with the aid of a similar transformation, then two-dimensional rogue wave solutions represented by the rational functions of the non-autonomous Kadomtsev-Petviashvili equation are constructed based on the Lump solution of the first kind of Kadomtsev-Petviashvili equation, and their evolutionary characteristics are illustrated by images through appropriately selecting the variable parameters and the dynamic stability of two-dimensional single rogue waves is numerically simulated by the fast Fourier transform algorithm. The obtained two-dimensional rogue waves, which are localized in both space and time, can be viewed as a two-dimensional analogue to the Peregrine soliton and thus are a natural candidate for describing the rogue wave phenomena. The method presented here provides enlightenment for searching for rogue wave excitation of (2 + 1)-dimensional nonlinear wave models.We show that two-dimensional rogue waves are localized in both space and time which arise from the zero background and then disappear into the zero background again. These rogue-wave solutions to the non-autonomous Kadomtsev-Petviashvili equation generalize the rogue waves of the nonlinear Schrödinger equation into two spatial dimensions, and they could play a role in physically understanding the rogue water waves in the ocean.

Keywords:

作者及机构信息

1.
浙江传媒学院智能媒体技术研究院, 杭州　310018

2.
浙江传媒学院, 浙江省影视媒体技术研究重点实验室, 杭州　310018

3.
浙江传媒学院网络数据中心, 杭州　310018

4.
中原工学院理学院, 郑州　450007

通信作者: 张解放, Zhangjief@cuz.edu.cn

基金项目: 国家自然科学基金(批准号: 61877053)资助的课题

Authors and contacts

1.
Institute of Intelligent Media Technology, Communication University of Zhejiang, Hangzhou 310018, China

2.
Zhejiang Provincial Key Laboratory of Film and Television Media Technology, Communication University of Zhejiang, Hangzhou 310018, China

3.
Network Data Center, Communication University of Zhejiang, Hangzhou 310018, China

4.
College of Science, Zhongyuan University of Technology, Zhengzhou 450007, China

Corresponding author: Zhang Jie-Fang, Zhangjief@cuz.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 61877053)

文章全文 : translate this paragraph

参考文献

[1]	Pelinovsky E, Kharf C 2008 Extreme Ocean Waves (Berlin: Springer)
[2]	Onorato M, Osborne A R, Serio M, Bertone S 2001 Phys. Rev. Lett. 86 5831 Google Scholar
[3]	Ginzburg N S, Rozental R M, Sergeev A S, Fedotov A E, Zotova I V, Tarakanov V P 2017 Phys. Rev. Lett. 119 034801 Google Scholar
[4]	Akhmediev N, Dudley J M, Solli D R, Turitsyn S K 2013 J. Opt. 15 060201 Google Scholar
[5]	Bludov Yu V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610 Google Scholar
[6]	Moslem W M 2011 Phys. Plasm. 18 032301 Google Scholar
[7]	Stenflo L, Marklund M 2010 J. Plasm. Phys. 76 293 Google Scholar
[8]	Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F 2013 Phys. Rep. 528 47 Google Scholar
[9]	Müller P, Garrett C, Osborne A 2005 Oceanography 18 66 Google Scholar
[10]	张解放, 戴朝卿 2016 65 050501 Google Scholar Zhang J F, Dai C Q 2016 Acta Phys. Sin 65 050501 Google Scholar
[11]	Hohmann R, Kuhl U, Stockmann H J, Kaplan L, Heller E J 2010 Phys. Rev. Lett. 104 093901 Google Scholar
[12]	Ganshin A N, Efimov V B, Kolmakov G V, Mezhov Deglin P V, McClintock E 2008 Phys. Rev. Lett. 101 065303 Google Scholar
[13]	Yan Z Y 2010 Commun. Theor. Phys. 54 947 Google Scholar
[14]	Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503 Google Scholar
[15]	Xia H, Maimbourg T, Punzmann H, Shats M 2012 Phys. Rev. Lett. 109 114502 Google Scholar
[16]	Solli R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054 Google Scholar
[17]	Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502 Google Scholar
[18]	Peregrine D H 1983 J. Aust. Math. Soc. Ser. B: Appl. Math. 25 16 Google Scholar
[19]	Akhmediev N, Ankiewicz A, Soto Crespo J M 2009 Phys. Rev. E 80 026601 Google Scholar
[20]	Kedziora D J, Ankiewicz A, Akhmediev N 2012 Phys. Rev. E 86 056602 Google Scholar
[21]	Ohta Y, Yang J 2012 Proc. R. Soc. A 468 1716 Google Scholar
[22]	Ankiewicz A, Soto Crespo J M, Akhmediev N 2010 Phys. Rev. E 81 046602 Google Scholar
[23]	Li L J, Wu Z W, Wang J H, He J S 2013 Annals of Physics 334 198 Google Scholar
[24]	Tao Y S, He J S 2012 Phys. Rev. E 85 026601 Google Scholar
[25]	Chen S 2013 Phys. Rev. E 88 023202 Google Scholar
[26]	Chan H N, Chow K W, Kedziora D J, Grimshaw R H J, Ding E 2014 Phys. Rev. E 89 032914 Google Scholar
[27]	Zhang Y S, Guo L J, He J S 2015 Lett. Math. Phys. 105 853 Google Scholar
[28]	Qiu D Q, He J, Zhang Y H, Porsezian K 2015 Proc. R. Soc. A 471 20150236 Google Scholar
[29]	He J S, Xu S W, Porsezian K 2012 J. Phs. Soc. Japan 81 124007 Google Scholar
[30]	Xu S W, He J S, Cheng Y, Porseizan K 2015 Math. Meth. Appli. Sci. 38 1106 Google Scholar
[31]	Chen S, Song L Y 2014 Phys. Lett. A 378 1228 Google Scholar
[32]	He J S, Wang L, Li L, Porsezian K, Erdélyi R 2014 Phys. Rev. E 89 062917 Google Scholar
[33]	Zha Q 2013 Phys. Scr. 87 065401 Google Scholar
[34]	Chen S, Soto Crespo J M, Baronio F, Grelu Ph, Mihalache D 2016 Opt. Express 24 15251 Google Scholar
[35]	Wang L H, Porsezian K, He J S 2013 Phys. Rev. E 87 053202 Google Scholar
[36]	Chen S, Mihalache D 2015 J. Phys. A: Math. Theor. 48 215202 Google Scholar
[37]	Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S 2014 Phys. Rev. Lett. 113 034101 Google Scholar
[38]	He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914 Google Scholar
[39]	Wang L H, He J S, Xu H, Wang J, Porsezian K 2017 Phys. Rev. E 95 042217 Google Scholar
[40]	Ohta Y, Yang J 2012 Phys. Rev. E 86 036604 Google Scholar
[41]	Ohta Y, Yang J 2013 J. Phys. A: Math. Theor. 46 105202 Google Scholar
[42]	Rao J G, Porsezian K, He J S 2017 Chaos 27 083115 Google Scholar
[43]	Guo L J, He J S, Wang L H, Cheng Y, Frantzeskakis D J, Kevrekidis P G 2020 Phys. Rev. Res. 2 033376 Google Scholar
[44]	Wen L L, Zhang H Q 2016 Nonlinear Dyn. 86 877 Google Scholar
[45]	Qiu D Q, Zhang Y S, He J S 2016 Commun. Nonlinear Sci. Numer. Simulat. 30 307 Google Scholar
[46]	Jia R R, Guo R 2019 Appl. Math. Lett. 93 117 Google Scholar
[47]	Kadomtsev B B, Petviashvili V I 1970 Sov. Phys. Dokl. 15 539
[48]	Ablowitz M J, Segur H 1979 J. Fluid Mech. 92 691 Google Scholar
[49]	Pelinovsky D E, Stepanyants Y A, Kivshar Y A 1995 Phys. Rev. E 51 5016 Google Scholar
[50]	Manakov S V, Zakharov V E, Bordag L A, Matveev V B 1977 Phys. Lett. A 63 205 Google Scholar
[51]	Krichever I 1978 Funct. Anal. and Appl. 12 59
[52]	Satsuma J, Ablowitz M J 1979 J. Math. Phys. 20 1496 Google Scholar
[53]	Pelinovsky D E, Stepanyants Y A 1993 JETP Lett. 57 24
[54]	Pelinovsky D E 1994 J. Math. Phys. 35 5820 Google Scholar
[55]	Ablowitz M J, Villarroel J 1997 Phys. Rev. Lett. 78 570 Google Scholar
[56]	Villarroel J, Ablowitz M J 1999 Comm. Math. Phys. 207 1 Google Scholar
[57]	Biondini G, Kodama Y 2003 J. Phys. A: Math. Gen. 36 10519 Google Scholar
[58]	Kodama Y 2004 J. Phys. A: Math. Gen. 37 11169 Google Scholar
[59]	Biondini G 2007 Phys. Rev. Lett. 99 064103 Google Scholar
[60]	Ma W X 2015 Phys. Lett. A 379 1975 Google Scholar
[61]	Singh N, Stepanyants Y 2016 Wave Motion 64 92 Google Scholar
[62]	Hu W C, Huang W H, L u, Z M, Stepanyants Y 2018 Wave Motion 77 243 Google Scholar
[63]	Wen X Y, Yan Z Y 2017 Commun. Nonlinear Sci. Numer. Simulat. 43 311 Google Scholar
[64]	Yang J Y, Ma W X 2017 Nonlinear Dyn. 89 1539 Google Scholar
[65]	Jia M, Lou S 2018 arXiv: 1803.01730 v1[nlin.SI]
[66]	Serkin V N, Hasegawa A 2000 Phys. Rev. Lett. 85 4502
[67]	Serkin V N, Hasegawa A, Belyaeva T L 2007 Phys. Rev. Lett. 98 074102 Google Scholar
[68]	Yan Z Y, Zhang X F, Liu W M 2011 Phys. Rev. A 84 023627 Google Scholar
[69]	Lou H G, Zhao D, He X 2009 , Phys. Rev. A 79 063802 Google Scholar
[70]	Zhang J F, Li Y S, Meng J P, Wu L, Malomed B A 2010 Phys. Rev. A 82 033614 Google Scholar
[71]	Dai C Q, Zhang J F 2010 Opt. Lett. 35 2651 Google Scholar
[72]	Serkin V N, Hasegawa A, Belyaeva T L 2010 Phys. Rev. A 81 023610 Google Scholar
[73]	Kibler B, Fatome J, Finot C, et al. 2010 Nat. Phys. 6 790 Google Scholar
[74]	Wu L, Zhang J F, Li L, Tian Q, Porsezian K 2008 Opt. Express 16 6352 Google Scholar
[75]	Tian Q, Wu L, Zhang J F, Malomed B A, Mihalache D, Liu W M 2011 Phys. Rev. E 83 016602 Google Scholar
[76]	David D, Levi D, Wintemitz P 1987 Stud. Appl. Math. 76 133 Google Scholar
[77]	Chan W L, Li K S, Li Y S 1992 J. Math. Phys. 33 3759 Google Scholar
[78]	Lü Z S, Chen Y N 2015 Eur. Phys. J. B 88 187 Google Scholar
[79]	Ilhan O A, Manafian J, Shahriaric M 2019 Comput. Math. App. 78 2429 Google Scholar

施引文献

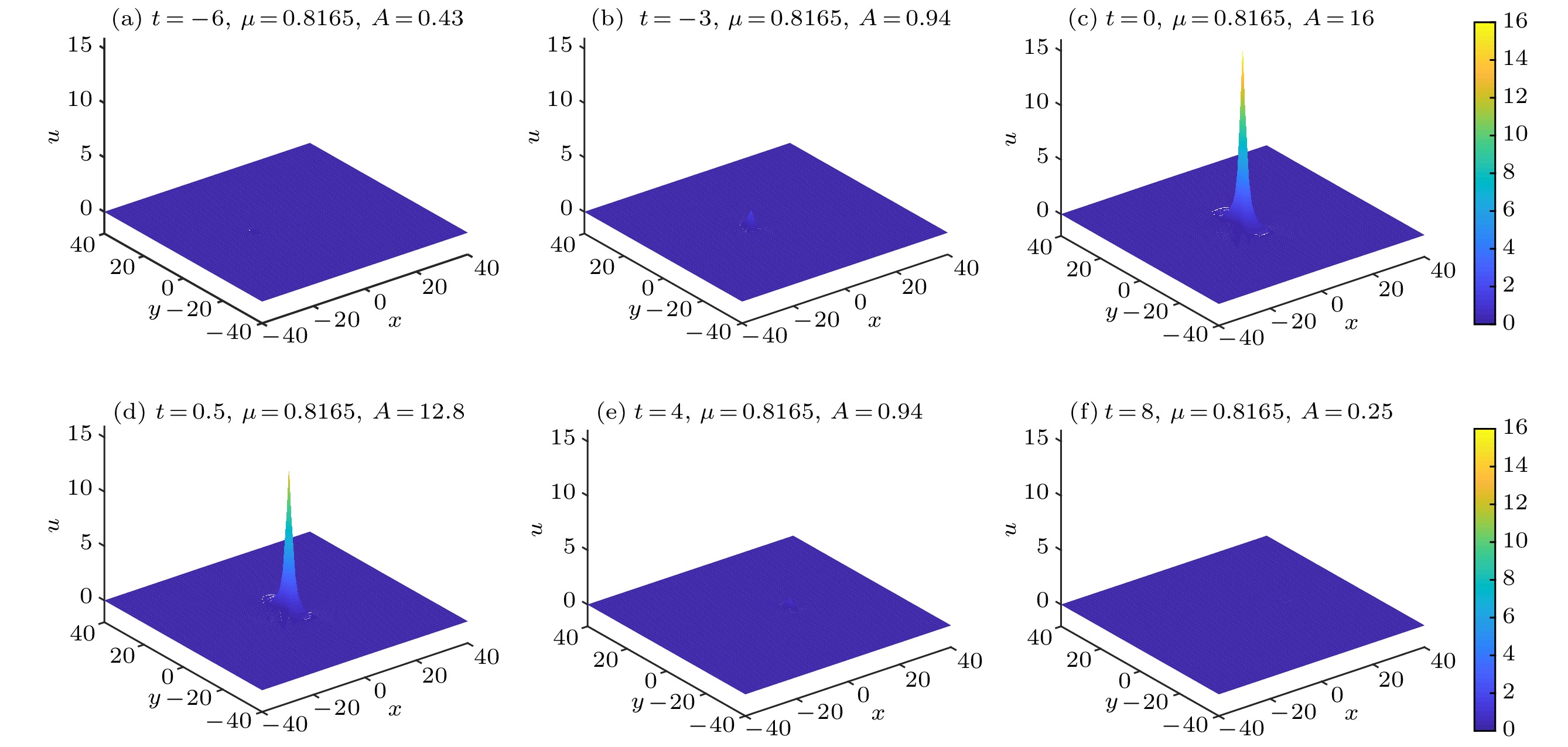
图 1 由(12)式所确定的非自治KP方程的二维单怪波演化　(a) $t \!=\! - 6$; (b)$t \!=\! - 3$; (c) $t \!=\! 0$; (d) $t \!=\! 0.5$; (e) $t \!=\! 4$; (f) $t \!=\! 8$

Fig. 1. Evolution of two-dimensional single rogue wave propagation given in Eq. (12) for non-autonomous KP equation: (a)$t = - 6$; (b) $t = - 3$; (c) $t = 0$; (d) $t = 0.5$; (e) $t = 4$; (f) $t = 8$.

下载: 全尺寸图片幻灯片

图 2 由(13)式所确定的非自治KP方程的二维单怪波演化　(a)$t = - 6$; (b)$t = - 3$; (c)$t = 0$; (d)$t = 0.5$; (e)$t = 4$; (f)$t = 8$

Fig. 2. Evolution of two-dimensional single rogue wave propagation given in Eq. (13) for non-autonomous KP equation: (a)$t = - 6$; (b)$t = - 3$; (c)$t = 0$; (d)$t = 0.5$; (e)$t = 4$; (f) $t = 8$.

下载: 全尺寸图片幻灯片

图 3 由(14)式所确定的非自治KP方程的二维单怪波演化　(a)$t = - 6$; (b) $t = - 3$; (c)$t = 0$; (d) $t = 0.5$; (e)$t = 4$; (f)$t = 8$

Fig. 3. Evolution of two-dimensional single rogue wave propagation given in Eq. (14) for non-autonomous KP equation: (a)$t = - 6$; (b) $t = - 3$; (c)$t = 0$; (d)$t = 0.5$; (e)$t = 4$; (f)$t = 8$.

下载: 全尺寸图片幻灯片

图 4 由(11)式所确定的非自治KP方程的二维双怪波演化(选取$k = 1/2, l = 1/2, n = 0, m = 1, \lambda = \varepsilon = 1, \nu = 1, \chi = 0, {\upsilon _x} = 2, {\upsilon _y} = 1, a = b = 0$)　(a)$t = - 6$; (b)$t = - 3$; (c)$t = 0$; (d) $t = 0.5$; (e)$t = 4$; (f)$t = 8$

Fig. 4. Time evolution of two-dimensional double rogue waves propagation given in Eq. (11) for non-autonomous KP equation when$k = 1/2, l = 1/2, n = 0, m = 1, $ $\lambda = \varepsilon = 1, \nu = 1, \chi = 0, {\upsilon _x} = 2, {\upsilon _y} = 1, a = b = 0$: (a)$t = - 6$; (b)$t = - 3$; (c)$t = 0$; (d) $t = 0.5$; (e)$t = 4$; (f)$t = 8$.

下载: 全尺寸图片幻灯片

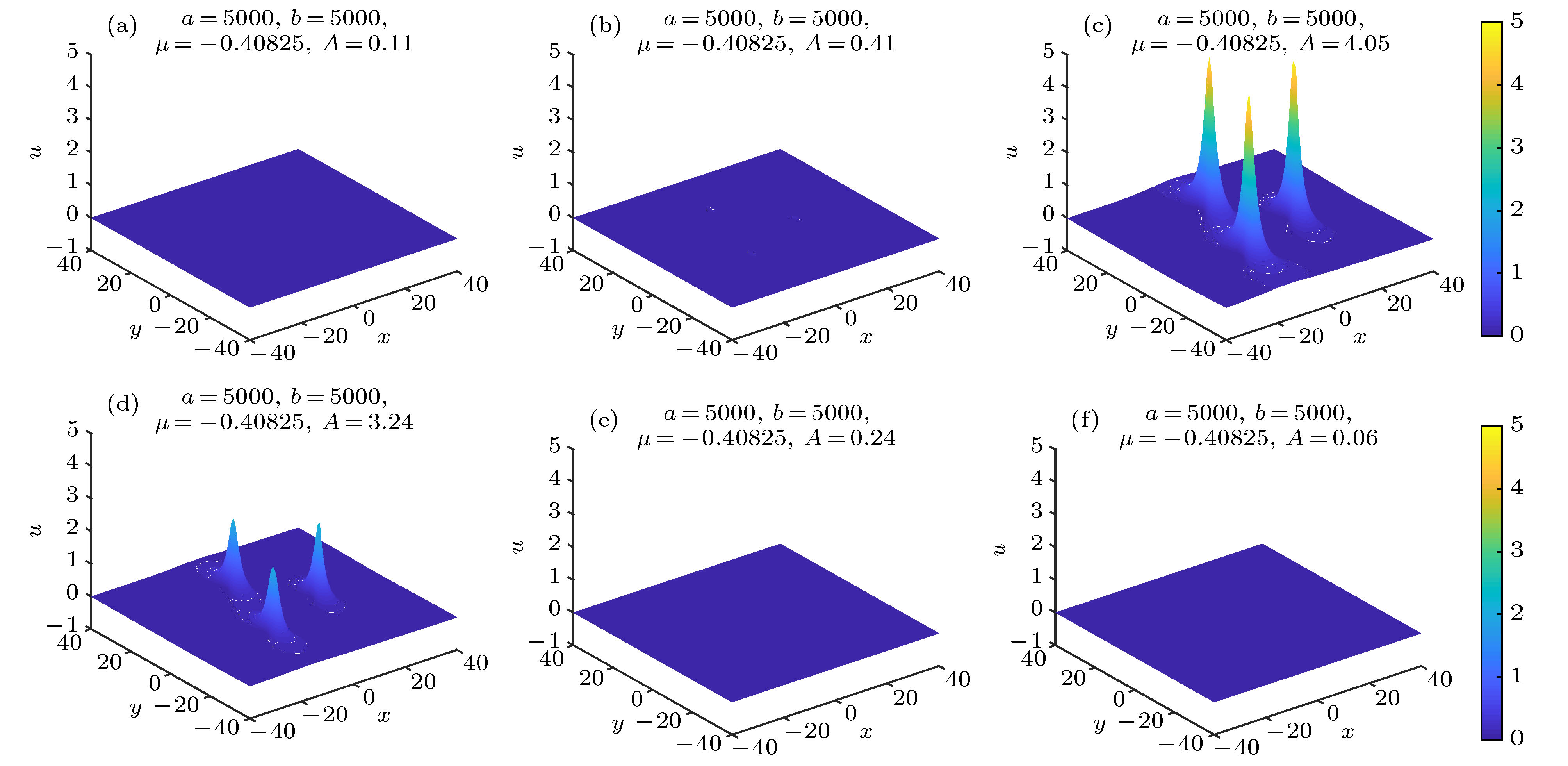
图 5 由(11)式所确定的非自治KP方程二维三怪波演化(选择$k = l = 1/2, n = 0, m = 1, $ $\lambda = \varepsilon = 1, \nu = 1, \chi = 0, {\upsilon _x} = 2, {\upsilon _y} = 2, a = 5000, b = 5000$)　(a) $t = - 6$; (b) $t = - 3$; (c) $t = 0$; (d) $t = 0.5$; (e) $t = 4$; (f) $t = 8$

Fig. 5. Time evolution of two-dimensional triple rogue waves propagation given in Eq. (11) for non-autonomous KP equation when $k = l = 1/2, n = 0, m = 1, \lambda = \varepsilon = 1, $ $\nu = 1, \chi = 0, {\upsilon _x} = 2, {\upsilon _y} = 1, a = 5000, b = 5000$: (a) $t = - 6$; (b) $t = - 3$; (c) $t = 0$; (d) $t = 0.5$; (e) $t = 4$; (f) $t = 8$.

下载: 全尺寸图片幻灯片

图 6 由(11)式所确定的二维双、三怪波(选取$k = 1/2, l = 1/2, n = 0, m = 1, $ $\lambda = 1, \varepsilon = 1, \nu = 1, \chi = 0, {\upsilon _x} = 2$, $\mu =0, \mu =0.8165, \mu =-0.8165$分别对应选取${\upsilon _y} = 0, {\upsilon _y} = - 2, {\upsilon _y} = 2$)

Fig. 6. Profiles of two-dimensional double and triple rogue waves given in Eq. (11) for non-autonomous KP equation when $k = 1/2, l = 1/2, n = 0, m = 1, \lambda = 1, \varepsilon = 1, \nu = 1, $ $\chi = 0, {\upsilon _x} = 2$,$\mu =0, \mu =0.8165, \mu =-0.8165$ correspond to ${\upsilon _y}{{ = 0}}, {\upsilon _y} = - 2, {\upsilon _y} = 2$, respectively.

下载: 全尺寸图片幻灯片

图 7 加了高斯白噪声扰动后由(15)式所确定的二维单怪波演化　(a) $t = - 5$; (b) $t = - {\rm{3}}$; (c) $t = - 1$; (d) $t = 0$; (e) $t = {2}.5$; (f) $t = 4$

Fig. 7. Evolution of two-dimensional single rogue wave determined by Eq. (15) after Gaussian white noise disturbance: (a) $t = - 5$; (b) $t = - {\rm{3}}$; (c) $t = - 1$; (d) $t = 0$; (e) $t = {2}.5$; (f) $t = 4$.

下载: 全尺寸图片幻灯片

图 8 加了高斯白噪声扰动后由(16)式所确定的二维单怪波演化　(a) $t = - 5$; (b) $t = - {\rm{3}}$, (c) $t = - 1$; (d) $t = 0$; (e) $t = {2}.5$; (f) $t = 4$

Fig. 8. Evolution of two-dimensional single rogue wave determined by Eq. (16) after Gaussian white noise disturbance: (a) $t = - 5$; (b) $t = - {\rm{3}}$; (c) $t = - 1$; (d) $t = 0$; (e) $t = {2}.5$; (f) $t = 4$.

下载: 全尺寸图片幻灯片

图 9 在时间区间[–5, 5] x-y平面上非自治KP方程的二维单怪波最大波动值和最小波动值的解析结果和数值计算模拟的对照图　(a)对应二维单怪波((15)式); (b)对应二维单怪波((16)式); (c)在(a)中加了高斯白噪声扰动; (d)在(b)中加高斯白噪声扰动

Fig. 9. Simulation diagram of the analytic and numerical results of the maximum and minimum fluctuations of two-dimensional single rogue waves for the non- autonomous KP equation in the x-y plane of the time interval [–5, 5]: (a) Corresponds to a two-dimensional single rogue wave (Eq. (15)); (b) Corresponds to a two- dimensional single rogue wave (Eq. (16)); (c) Gaussian white noise is added in panel (a); (d) Gaussian white noise is added in panel (b).

下载: 全尺寸图片幻灯片

map

[1]	Pelinovsky E, Kharf C 2008 Extreme Ocean Waves (Berlin: Springer)
[2]	Onorato M, Osborne A R, Serio M, Bertone S 2001 Phys. Rev. Lett. 86 5831 Google Scholar
[3]	Ginzburg N S, Rozental R M, Sergeev A S, Fedotov A E, Zotova I V, Tarakanov V P 2017 Phys. Rev. Lett. 119 034801 Google Scholar
[4]	Akhmediev N, Dudley J M, Solli D R, Turitsyn S K 2013 J. Opt. 15 060201 Google Scholar
[5]	Bludov Yu V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610 Google Scholar
[6]	Moslem W M 2011 Phys. Plasm. 18 032301 Google Scholar
[7]	Stenflo L, Marklund M 2010 J. Plasm. Phys. 76 293 Google Scholar
[8]	Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F 2013 Phys. Rep. 528 47 Google Scholar
[9]	Müller P, Garrett C, Osborne A 2005 Oceanography 18 66 Google Scholar
[10]	张解放, 戴朝卿 2016 65 050501 Google Scholar Zhang J F, Dai C Q 2016 Acta Phys. Sin 65 050501 Google Scholar
[11]	Hohmann R, Kuhl U, Stockmann H J, Kaplan L, Heller E J 2010 Phys. Rev. Lett. 104 093901 Google Scholar
[12]	Ganshin A N, Efimov V B, Kolmakov G V, Mezhov Deglin P V, McClintock E 2008 Phys. Rev. Lett. 101 065303 Google Scholar
[13]	Yan Z Y 2010 Commun. Theor. Phys. 54 947 Google Scholar
[14]	Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503 Google Scholar
[15]	Xia H, Maimbourg T, Punzmann H, Shats M 2012 Phys. Rev. Lett. 109 114502 Google Scholar
[16]	Solli R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054 Google Scholar
[17]	Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502 Google Scholar
[18]	Peregrine D H 1983 J. Aust. Math. Soc. Ser. B: Appl. Math. 25 16 Google Scholar
[19]	Akhmediev N, Ankiewicz A, Soto Crespo J M 2009 Phys. Rev. E 80 026601 Google Scholar
[20]	Kedziora D J, Ankiewicz A, Akhmediev N 2012 Phys. Rev. E 86 056602 Google Scholar
[21]	Ohta Y, Yang J 2012 Proc. R. Soc. A 468 1716 Google Scholar
[22]	Ankiewicz A, Soto Crespo J M, Akhmediev N 2010 Phys. Rev. E 81 046602 Google Scholar
[23]	Li L J, Wu Z W, Wang J H, He J S 2013 Annals of Physics 334 198 Google Scholar
[24]	Tao Y S, He J S 2012 Phys. Rev. E 85 026601 Google Scholar
[25]	Chen S 2013 Phys. Rev. E 88 023202 Google Scholar
[26]	Chan H N, Chow K W, Kedziora D J, Grimshaw R H J, Ding E 2014 Phys. Rev. E 89 032914 Google Scholar
[27]	Zhang Y S, Guo L J, He J S 2015 Lett. Math. Phys. 105 853 Google Scholar
[28]	Qiu D Q, He J, Zhang Y H, Porsezian K 2015 Proc. R. Soc. A 471 20150236 Google Scholar
[29]	He J S, Xu S W, Porsezian K 2012 J. Phs. Soc. Japan 81 124007 Google Scholar
[30]	Xu S W, He J S, Cheng Y, Porseizan K 2015 Math. Meth. Appli. Sci. 38 1106 Google Scholar
[31]	Chen S, Song L Y 2014 Phys. Lett. A 378 1228 Google Scholar
[32]	He J S, Wang L, Li L, Porsezian K, Erdélyi R 2014 Phys. Rev. E 89 062917 Google Scholar
[33]	Zha Q 2013 Phys. Scr. 87 065401 Google Scholar
[34]	Chen S, Soto Crespo J M, Baronio F, Grelu Ph, Mihalache D 2016 Opt. Express 24 15251 Google Scholar
[35]	Wang L H, Porsezian K, He J S 2013 Phys. Rev. E 87 053202 Google Scholar
[36]	Chen S, Mihalache D 2015 J. Phys. A: Math. Theor. 48 215202 Google Scholar
[37]	Baronio F, Conforti M, Degasperis A, Lombardo S, Onorato M, Wabnitz S 2014 Phys. Rev. Lett. 113 034101 Google Scholar
[38]	He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914 Google Scholar
[39]	Wang L H, He J S, Xu H, Wang J, Porsezian K 2017 Phys. Rev. E 95 042217 Google Scholar
[40]	Ohta Y, Yang J 2012 Phys. Rev. E 86 036604 Google Scholar
[41]	Ohta Y, Yang J 2013 J. Phys. A: Math. Theor. 46 105202 Google Scholar
[42]	Rao J G, Porsezian K, He J S 2017 Chaos 27 083115 Google Scholar
[43]	Guo L J, He J S, Wang L H, Cheng Y, Frantzeskakis D J, Kevrekidis P G 2020 Phys. Rev. Res. 2 033376 Google Scholar
[44]	Wen L L, Zhang H Q 2016 Nonlinear Dyn. 86 877 Google Scholar
[45]	Qiu D Q, Zhang Y S, He J S 2016 Commun. Nonlinear Sci. Numer. Simulat. 30 307 Google Scholar
[46]	Jia R R, Guo R 2019 Appl. Math. Lett. 93 117 Google Scholar
[47]	Kadomtsev B B, Petviashvili V I 1970 Sov. Phys. Dokl. 15 539
[48]	Ablowitz M J, Segur H 1979 J. Fluid Mech. 92 691 Google Scholar
[49]	Pelinovsky D E, Stepanyants Y A, Kivshar Y A 1995 Phys. Rev. E 51 5016 Google Scholar
[50]	Manakov S V, Zakharov V E, Bordag L A, Matveev V B 1977 Phys. Lett. A 63 205 Google Scholar
[51]	Krichever I 1978 Funct. Anal. and Appl. 12 59
[52]	Satsuma J, Ablowitz M J 1979 J. Math. Phys. 20 1496 Google Scholar
[53]	Pelinovsky D E, Stepanyants Y A 1993 JETP Lett. 57 24
[54]	Pelinovsky D E 1994 J. Math. Phys. 35 5820 Google Scholar
[55]	Ablowitz M J, Villarroel J 1997 Phys. Rev. Lett. 78 570 Google Scholar
[56]	Villarroel J, Ablowitz M J 1999 Comm. Math. Phys. 207 1 Google Scholar
[57]	Biondini G, Kodama Y 2003 J. Phys. A: Math. Gen. 36 10519 Google Scholar
[58]	Kodama Y 2004 J. Phys. A: Math. Gen. 37 11169 Google Scholar
[59]	Biondini G 2007 Phys. Rev. Lett. 99 064103 Google Scholar
[60]	Ma W X 2015 Phys. Lett. A 379 1975 Google Scholar
[61]	Singh N, Stepanyants Y 2016 Wave Motion 64 92 Google Scholar
[62]	Hu W C, Huang W H, L u, Z M, Stepanyants Y 2018 Wave Motion 77 243 Google Scholar
[63]	Wen X Y, Yan Z Y 2017 Commun. Nonlinear Sci. Numer. Simulat. 43 311 Google Scholar
[64]	Yang J Y, Ma W X 2017 Nonlinear Dyn. 89 1539 Google Scholar
[65]	Jia M, Lou S 2018 arXiv: 1803.01730 v1[nlin.SI]
[66]	Serkin V N, Hasegawa A 2000 Phys. Rev. Lett. 85 4502
[67]	Serkin V N, Hasegawa A, Belyaeva T L 2007 Phys. Rev. Lett. 98 074102 Google Scholar
[68]	Yan Z Y, Zhang X F, Liu W M 2011 Phys. Rev. A 84 023627 Google Scholar
[69]	Lou H G, Zhao D, He X 2009 , Phys. Rev. A 79 063802 Google Scholar
[70]	Zhang J F, Li Y S, Meng J P, Wu L, Malomed B A 2010 Phys. Rev. A 82 033614 Google Scholar
[71]	Dai C Q, Zhang J F 2010 Opt. Lett. 35 2651 Google Scholar
[72]	Serkin V N, Hasegawa A, Belyaeva T L 2010 Phys. Rev. A 81 023610 Google Scholar
[73]	Kibler B, Fatome J, Finot C, et al. 2010 Nat. Phys. 6 790 Google Scholar
[74]	Wu L, Zhang J F, Li L, Tian Q, Porsezian K 2008 Opt. Express 16 6352 Google Scholar
[75]	Tian Q, Wu L, Zhang J F, Malomed B A, Mihalache D, Liu W M 2011 Phys. Rev. E 83 016602 Google Scholar
[76]	David D, Levi D, Wintemitz P 1987 Stud. Appl. Math. 76 133 Google Scholar
[77]	Chan W L, Li K S, Li Y S 1992 J. Math. Phys. 33 3759 Google Scholar
[78]	Lü Z S, Chen Y N 2015 Eur. Phys. J. B 88 187 Google Scholar
[79]	Ilhan O A, Manafian J, Shahriaric M 2019 Comput. Math. App. 78 2429 Google Scholar

[1]	饶继光, 陈生安, 吴昭君, 贺劲松. 空间位移$\mathcal{PT}$对称非局域非线性薛定谔方程的高阶怪波解. , 2023, 72(10): 104204. doi: 10.7498/aps.72.20222298
[2]	张解放, 俞定国, 金美贞. 二维自相似变换理论和线怪波激发. , 2022, 71(1): 014205. doi: 10.7498/aps.71.20211417
[3]	张解放, 俞定国, 金美贞. (2+1)维Zakharov方程的自相似变换和线怪波簇激发. , 2022, 71(8): 084204. doi: 10.7498/aps.71.20211181
[4]	李敏, 王博婷, 许韬, 水涓涓. 四阶色散非线性薛定谔方程的明暗孤立波和怪波的形成机制. , 2020, 69(1): 010502. doi: 10.7498/aps.69.20191384
[5]	张解放, 金美贞. Fokas系统的怪波激发. , 2020, 69(21): 214203. doi: 10.7498/aps.69.20200710
[6]	焦小玉, 贾曼, 安红利. 一类扰动Kadomtsev-Petviashvili方程的雅可比椭圆函数解的收敛性探讨. , 2019, 68(14): 140201. doi: 10.7498/aps.68.20190333
[7]	王思佳, 顾澄琳, 刘博文, 宋有建, 钱程, 胡明列, 柴路, 王清月. 利用非线性脉冲预整形实现脉冲快速自相似放大. , 2013, 62(14): 140601. doi: 10.7498/aps.62.140601
[8]	陆大全, 胡巍. 椭圆响应强非局域非线性介质中的二维异步分数傅里叶变换及光束传输特性. , 2013, 62(8): 084211. doi: 10.7498/aps.62.084211
[9]	仲生仁. 尘埃等离子体中非线性波的叠加效应及稳定性问题. , 2010, 59(4): 2178-2181. doi: 10.7498/aps.59.2178
[10]	邓一鑫, 涂成厚, 吕福云. 非线性偏振旋转锁模自相似脉冲光纤激光器的研究. , 2009, 58(5): 3173-3178. doi: 10.7498/aps.58.3173
[11]	孟立民, 滕爱萍, 李英骏, 程涛, 张杰. 基于自相似模型的二维X射线激光等离子体流体力学. , 2009, 58(8): 5436-5442. doi: 10.7498/aps.58.5436
[12]	廖龙光, 付虹, 傅秀军. 十二次对称准周期结构的自相似变换及准晶胞构造. , 2009, 58(10): 7088-7093. doi: 10.7498/aps.58.7088
[13]	冯杰, 徐文成, 刘伟慈, 李书贤, 刘颂豪. 高阶色散效应常系数Ginzburg-Landau方程自相似脉冲演化的解析分析. , 2008, 57(8): 4978-4983. doi: 10.7498/aps.57.4978
[14]	赖小明, 卞保民, 杨玲, 杨娟, 卞牛, 李振华, 贺安之. 非奇异宇宙的理想气体自相似模型. , 2008, 57(12): 7955-7962. doi: 10.7498/aps.57.7955
[15]	冯杰, 徐文成, 李书贤, 陈伟成, 宋方, 申民常, 刘颂豪. 色散渐减光纤中Ginzburg-Landau方程的自相似脉冲演化的解析解. , 2007, 56(10): 5835-5842. doi: 10.7498/aps.56.5835
[16]	来娴静, 张解放. 两类2+1维非线性波动方程的线性叠加解. , 2004, 53(12): 4065-4069. doi: 10.7498/aps.53.4065
[17]	董全林, 刘彬. 在伽利略坐标变换下的二端面弹性转轴相似动力学方程. , 2002, 51(10): 2191-2196. doi: 10.7498/aps.51.2191
[18]	闫振亚, 张鸿庆. 具有阻尼项的非线性波动方程的相似约化. , 2000, 49(11): 2113-2117. doi: 10.7498/aps.49.2113
[19]	范恩贵, 张鸿庆. 非线性波动方程的孤波解. , 1997, 46(7): 1254-1258. doi: 10.7498/aps.46.1254
[20]	张珉, 陶瑞宝, 周世勋. 具有自相似结构的非均匀复合媒质质量分布的标度指数. , 1988, 37(12): 1987-1992. doi: 10.7498/aps.37.1987

计量

文章访问数: 6124
PDF下载量: 106
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

非自治Kadomtsev-Petviashvili方程的自相似变换和二维怪波构造