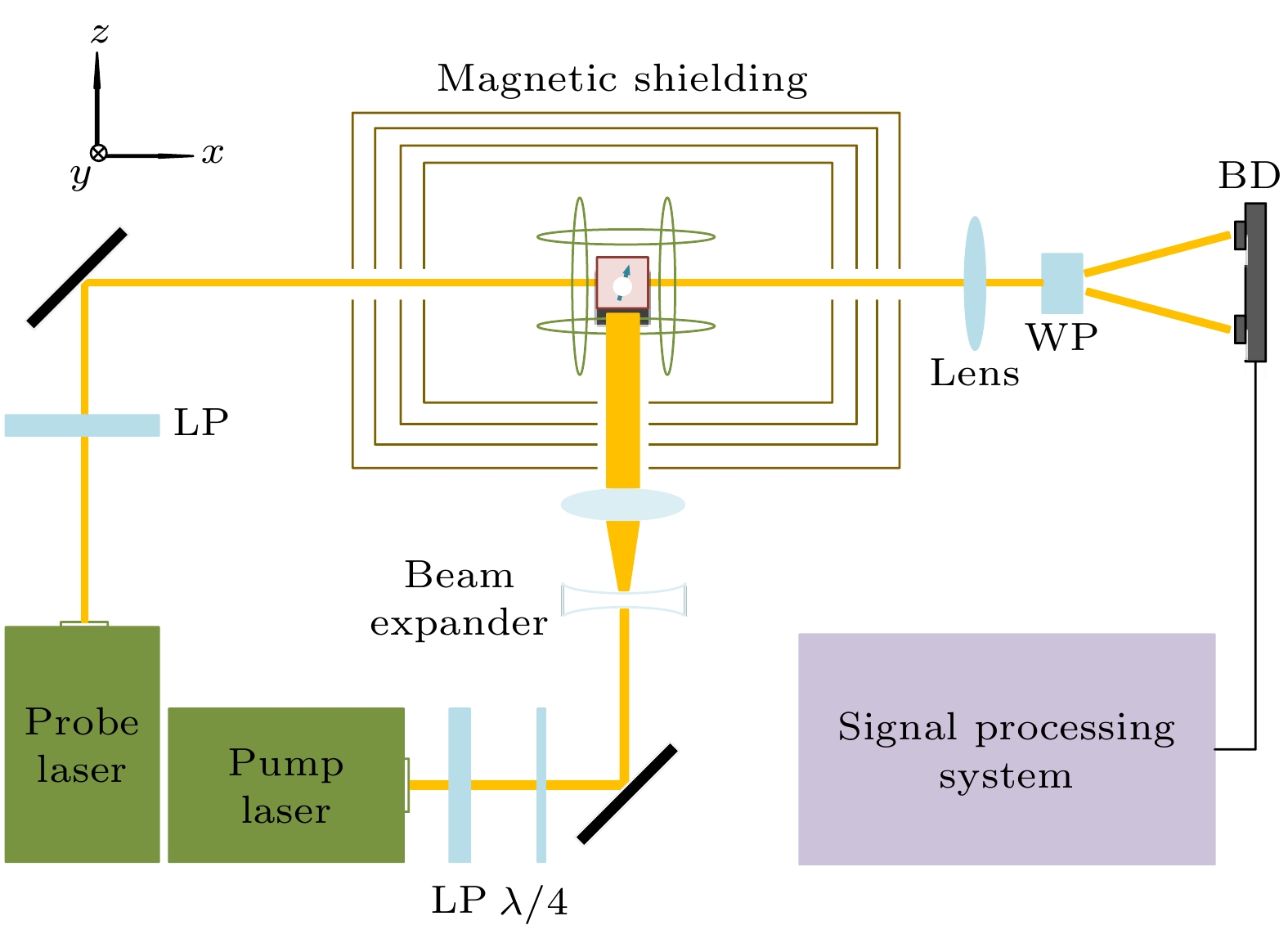
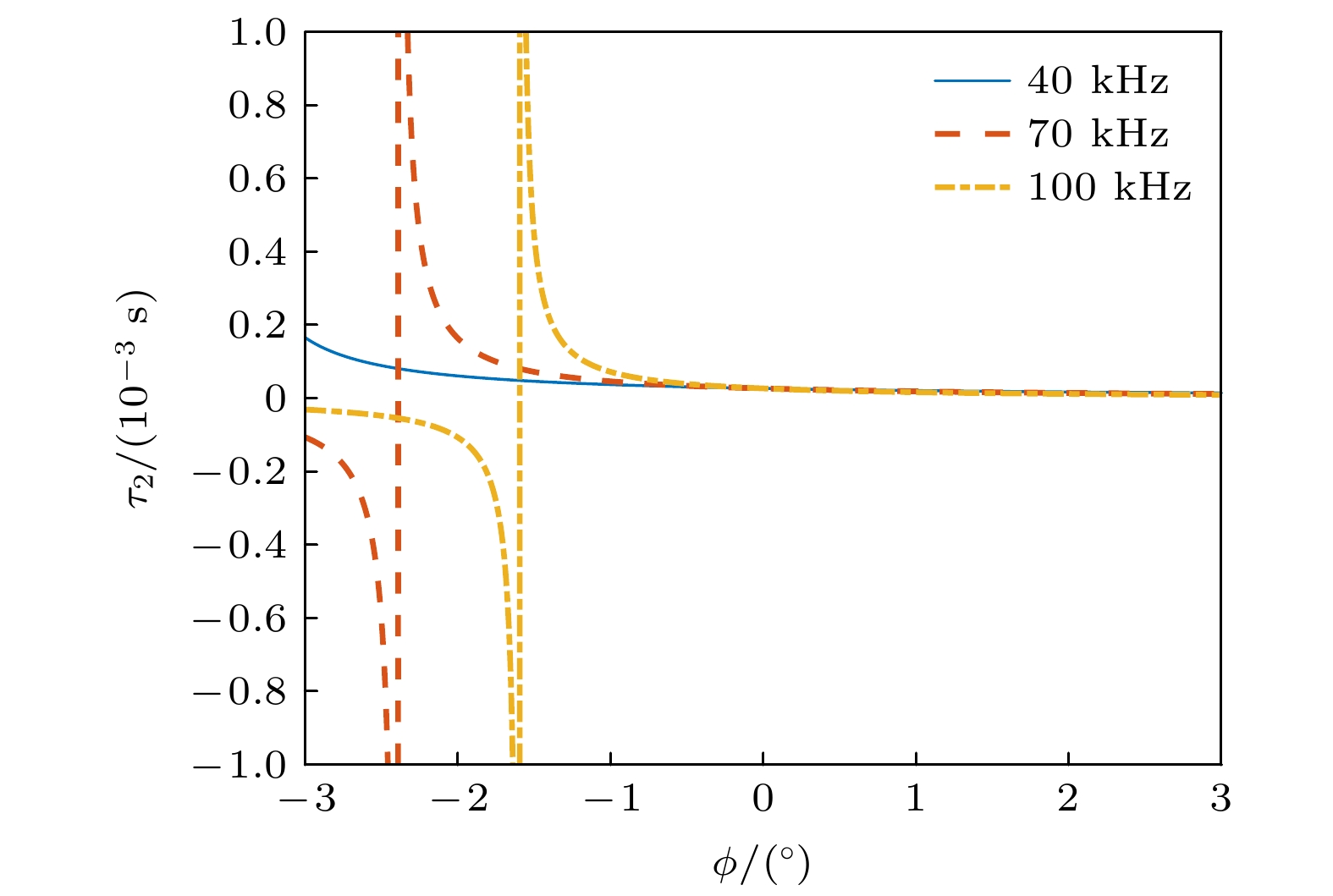
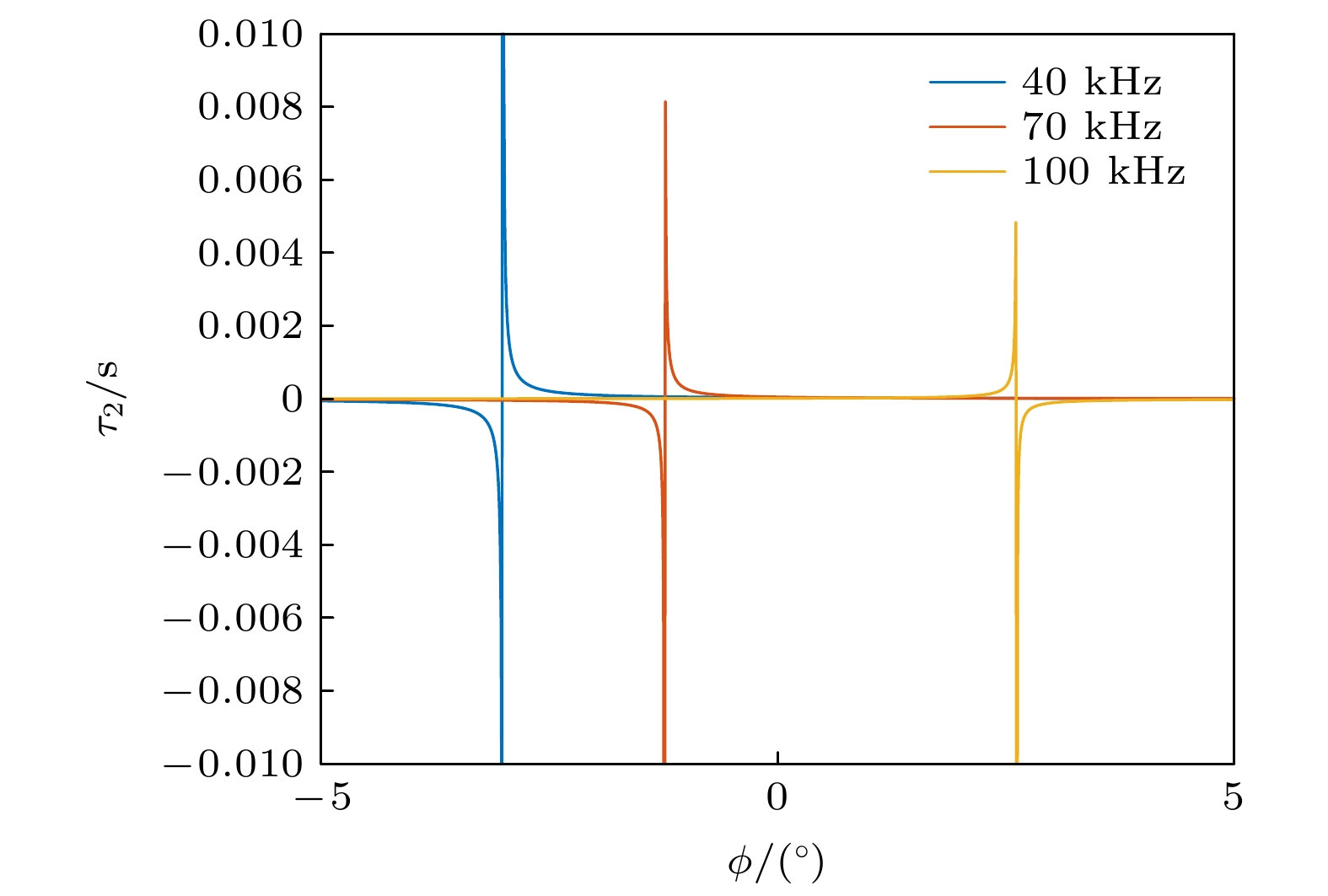
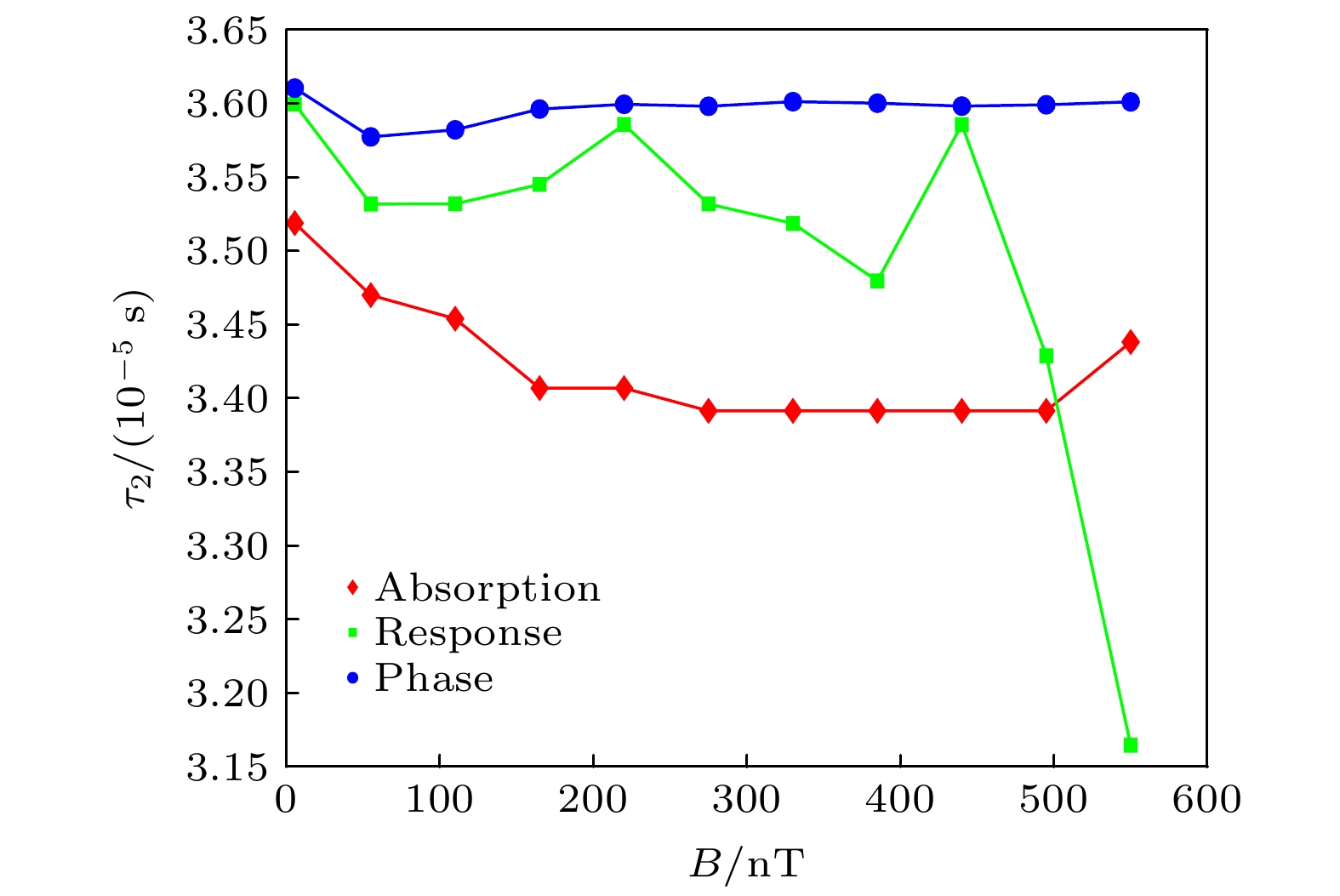
-
The spin relaxation time of alkali atoms in nuclear magnetic resonance gyroscope is usually on the order of 10–5 s, which is much less than that in atomic magnetometers. The response of electron paramagnetic resonance signals of atoms with short relaxation time is asymmetric in different directions under oscillating magnetic fields, which makes the measurement results of atomic transverse relaxation time and Larmor frequency different. In this work this phenomenon is analyzed based on Bloch equation theory and the theoretical correction is given. The shorter the relaxation time, the greater the differences of the response intensity and resonance frequency of the electron paramagnetic resonance signal under different magnetic field directions will be. Using this property, the transmission delay time of the system can be measured accurately. In this paper proposed is a method of measuring transverse relaxation time based on the difference between signal phases in X-axis direction and Y
-axis direction, which can accurately and quickly measure very short transverse relaxation time. The difference between the half-width fitting method and the phase measurement method is compared by measuring the transverse relaxation times of 87Rb atoms under different magnetic field intensities. The half-width fitting method is greatly affected by the transmission delay time and has its measurement limit. The phase measurement method is greatly affected by the angle of the probe light, but the measurement range is wider and the anti-magnetic interference ability is stronger. -
Keywords:
- atomic gyroscope /
- Bloch equation /
- amplitude-frequency response /
- transverse relaxation time
[1] D. Titterton, J. Weston 2004 IEEE Aerosp. El. Sys. Mag. 20 33
[2] Girao P M B S, Postolache O A, Faria J A B, Pereira J M C D 2001 IEEE Sens. J. 1 322
Google Scholar
[3] Fang J C, Qin J 2012 Sensors 12 6331
Google Scholar
[4] Schmidt G, Phillips R 2011 NATO Lecture Series 116 1
[5] Knappe S, Shah V, Schwindt P, Liew L, Hollberg L A, Moreland J 2004 Appl. Phys. L 85 1460
Google Scholar
[6] Kornack T W, Ghosh R K, Romalis M V 2005 Phys. Rev. L 95 230801
Google Scholar
[7] Shkel A 2005 Gps World 24 810
[8] Kominis I K, Kornack T W, Allred J C, Romalis M V 2003 Nature 422 596
Google Scholar
[9] Fang J C, Qin J 2012 Sensor 12 6331
[10] Meyer D, Larsen M 2014 Gyroscopy Navigation 5 75
Google Scholar
[11] Eklund E J 2008 Ph. D. Dissertation (Irvine: University of California)
[12] Roberts G J, Baird P, Brimicombe M, Sandars P, Selby D, Stacey D 1980 J. Phys B-At. Mol. Opt. 13 1389
Google Scholar
[13] Vershovskii A K, Litmanovich Y A, Pazgalev A S, Peshekhonov V G 2018 Gyroscopy Navigation 9 162
Google Scholar
[14] Colegrove F D, Schearer L D, Walters G K 1963 Phys. Rev. 132 2561
Google Scholar
[15] Schmiedeskamp J, Heil W, Otten E W, Kremer R K, Simon A, Zimmer J 2006 EUR. Phys. J. D 38 427
Google Scholar
[16] Meiboom S, Gill D 1958 Rev. Sci. Instrum. 29 688
Google Scholar
[17] Robert L. Vold 1972 J. Chem. Phys. 56 3210
Google Scholar
[18] Freeman R, Hill H, Kaptein R J. Magn. Reson. 7 82
[19] Xu S, Crawford C W, Rochester S, Yashchuk V, Budker D, Pines A 2008 Phys. Rev. A 78 013404
Google Scholar
[20] Gundeti V M 2015 Ph. D. Dissertation (Irvine: University of California)
[21] Freed J H 1972 Annu. Rev. Phys. Chem. 23 265
Google Scholar
[22] Bloch F 1946 Phys. Rev. 70 460
Google Scholar
[23] Torrey H C 1956 Phys. Rev. 104 563
Google Scholar
[24] Jiménez-Martínez R, Kołodyński J, Troullinou C, Lucivero V G, Kong J, Mitchell 2018 Phys. Rev. Lett. 120 040503
Google Scholar
-
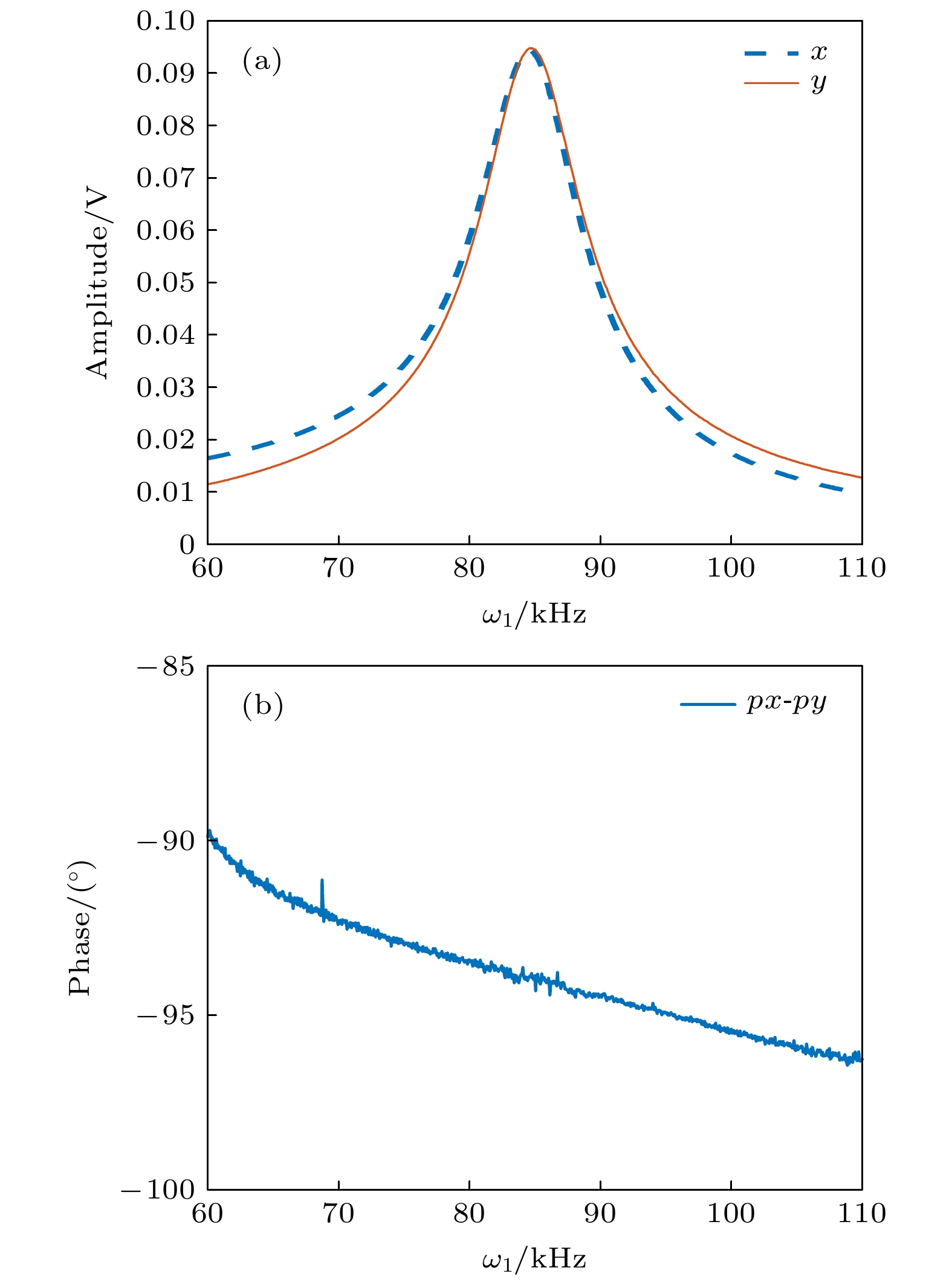
图 1 振荡场与旋转场的幅频响应 (a)
$ {\tau }_{2}=10\text{ μs} $ ; (b)$ {\tau }_{2}=20\text{ μs} $ ; (c)$ {\tau }_{2}=50\text{ μs} $ ; (d)$ {\tau }_{2}=100\text{ μs} $ Figure 1. Amplitude-frequency responses of oscillating and rotating fields (a)
$ {\tau }_{2}=10\text{ μs} $ ; (b)$ {\tau }_{2}=20\text{ μs} $ ; (c)$ {\tau }_{2}=50\text{ μs} $ ; (d)$ {\tau }_{2}=100\text{ μs} $ .
图 2 偏转角度对测量精度的影响
Figure 2. Effect of deflection angle on measurement accuracy.
图 3 实验装置
Figure 3. Experiment settings.
图 4 幅频及相位响应曲线测量 (a) 幅频响应; (b) 相位响应
Figure 4. Amplitude-frequency and phase-frequency curve measurement (a) Amplitude-frequency curve; (b) phase-frequency curve.
图 5 系统延迟时间测量
Figure 5. System delay time measurement.
图 6 幅频特性测量曲线
Figure 6. Amplitude-frequency curve measurement.
图 7 探测光偏移角对弛豫时间测量的影响
Figure 7. The influence of optical offset Angle on relaxation time measurement.
图 8 不同方法测量结果随磁场强度的变化
Figure 8. Variation of measurement results with magnetic field intensity by different methods.
-
[1] D. Titterton, J. Weston 2004 IEEE Aerosp. El. Sys. Mag. 20 33
[2] Girao P M B S, Postolache O A, Faria J A B, Pereira J M C D 2001 IEEE Sens. J. 1 322
Google Scholar
[3] Fang J C, Qin J 2012 Sensors 12 6331
Google Scholar
[4] Schmidt G, Phillips R 2011 NATO Lecture Series 116 1
[5] Knappe S, Shah V, Schwindt P, Liew L, Hollberg L A, Moreland J 2004 Appl. Phys. L 85 1460
Google Scholar
[6] Kornack T W, Ghosh R K, Romalis M V 2005 Phys. Rev. L 95 230801
Google Scholar
[7] Shkel A 2005 Gps World 24 810
[8] Kominis I K, Kornack T W, Allred J C, Romalis M V 2003 Nature 422 596
Google Scholar
[9] Fang J C, Qin J 2012 Sensor 12 6331
[10] Meyer D, Larsen M 2014 Gyroscopy Navigation 5 75
Google Scholar
[11] Eklund E J 2008 Ph. D. Dissertation (Irvine: University of California)
[12] Roberts G J, Baird P, Brimicombe M, Sandars P, Selby D, Stacey D 1980 J. Phys B-At. Mol. Opt. 13 1389
Google Scholar
[13] Vershovskii A K, Litmanovich Y A, Pazgalev A S, Peshekhonov V G 2018 Gyroscopy Navigation 9 162
Google Scholar
[14] Colegrove F D, Schearer L D, Walters G K 1963 Phys. Rev. 132 2561
Google Scholar
[15] Schmiedeskamp J, Heil W, Otten E W, Kremer R K, Simon A, Zimmer J 2006 EUR. Phys. J. D 38 427
Google Scholar
[16] Meiboom S, Gill D 1958 Rev. Sci. Instrum. 29 688
Google Scholar
[17] Robert L. Vold 1972 J. Chem. Phys. 56 3210
Google Scholar
[18] Freeman R, Hill H, Kaptein R J. Magn. Reson. 7 82
[19] Xu S, Crawford C W, Rochester S, Yashchuk V, Budker D, Pines A 2008 Phys. Rev. A 78 013404
Google Scholar
[20] Gundeti V M 2015 Ph. D. Dissertation (Irvine: University of California)
[21] Freed J H 1972 Annu. Rev. Phys. Chem. 23 265
Google Scholar
[22] Bloch F 1946 Phys. Rev. 70 460
Google Scholar
[23] Torrey H C 1956 Phys. Rev. 104 563
Google Scholar
[24] Jiménez-Martínez R, Kołodyński J, Troullinou C, Lucivero V G, Kong J, Mitchell 2018 Phys. Rev. Lett. 120 040503
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4330
- PDF Downloads: 77
- Cited By: 0
