-
The constant phase shift
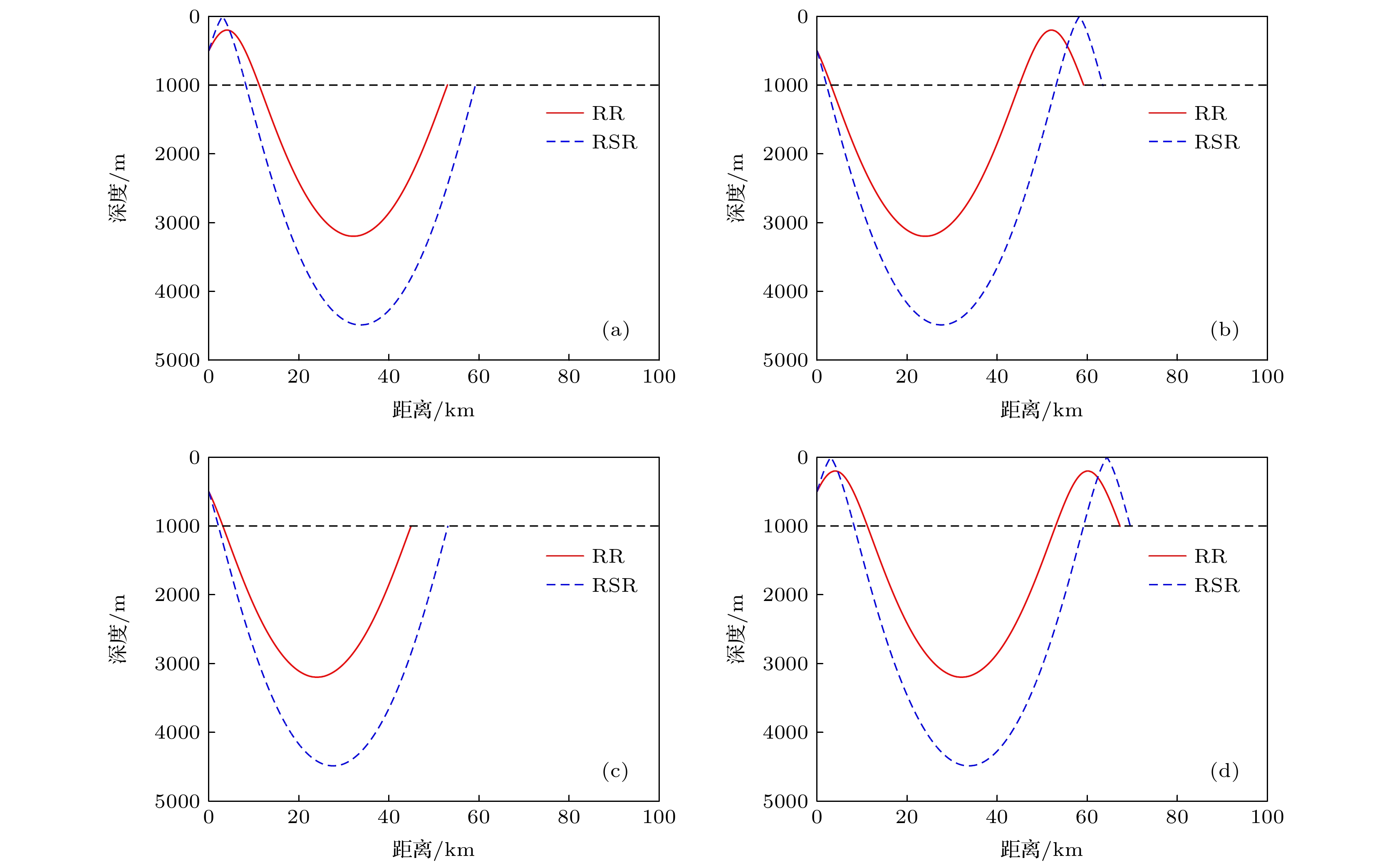
$- {{\text{π}}}/{2}$ generated by a turning point is an ideal approximation under high frequency conditions. In fact, when sound waves pass through a turning point, it will travel horizontally for a certain distance in the form of inhomogeneous plane wave and then be refracted back. At this time, a functional phase shift should also be included at the turning point. In addition, a refracted ray will bring about reflection phase shift when the turning point is close to the waveguide edge. These two kinds of phase shifts which are associated with the diffraction phenomenon are called diffraction phase shifts in this paper and are more notable when the frequency goes down. In order to accurately obtain the caustic structure at low frequency, the diffraction phase shift is used to correct the classical ray theory in calculating ray skip distance, traveling time, and group velocity in this work. On this basis, a simple and explicit analytical model is proposed which is suitable for calculating the low frequency deep water caustics. The numerical study of the first upper convergence zone in the complete deep water sound channel shows that there are three caustic lines in the refracted-refracted (RR) convergence zone and four caustic lines in the refracted surface-reflected (RSR) convergence zone under the condition of high frequency hypothesis. When the diffraction phase shifts at low frequency are included, and compares with high frequency results, it is found that the horizontal beam displacement caused by the reflection phase shift will make the RR caustics horizontally move towards the source and also lead the RSR rays to generate several new caustics, while the beam displacement caused by sound propagating in the form of inhomogeneous plan wave will make the RR caustics horizontally move away from the sound source. Accompanied with the increased frequency, the diffraction effect will decrease, and the caustic structure gradually tends to the classical ray theory results. The reliability of the correction results is verified by the normal mode theory. The model proposed in this work makes up for the deficiency of classical ray theory.[1] Munk W H 1974 J. Acoust. Soc. Am. 55 220
Google Scholar
[2] Hale F E 1961 J. Acoust. Soc. Am. 33 456
Google Scholar
[3] Brekhovskih L M 1980 Waves in Layered Media (2nd Ed.) (New York: Academic Press) p377
[4] Urick R J 1965 J. Acoust. Soc. Am. 38 348
Google Scholar
[5] 张仁和 1980 声学学报 1 28
Google Scholar
Zhang R H 1980 Acta Acust. 1 28
Google Scholar
[6] 张仁和 1982 声学学报 7 75
Google Scholar
Zhang R H 1982 Acta Acust. 7 75
Google Scholar
[7] 张仁和 1988 声学学报 13 101
Google Scholar
Zhang R H 1988 Acta Acust. 13 101
Google Scholar
[8] Bongiovanni K P, Siegmann W L 1996 J. Acoust. Soc. Am. 100 3033
Google Scholar
[9] 徐传秀 2017 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Xu C X 2017 Ph. D. Dissertation (Harbin: Harbin Engineering University) (in Chinese)
[10] 朴胜春, 栗子洋, 王笑寒, 张明辉 2021 70 024301
Google Scholar
Piao S C, Li Z Y, Wang X H, Zhang M H 2021 Acta Phys. Sin. 70 024301
Google Scholar
[11] 张青青, 李整林, 秦继兴, 李文, 吴双林 2020 声学学报 45 458
Google Scholar
Zhang Q Q, Li Z L, Qin J X, Li W, Wu S L 2020 Acta Acust. 45 458
Google Scholar
[12] 张鹏, 李整林, 吴立新, 张仁和, 秦继兴 2019 68 014301
Google Scholar
Zhang P, Li Z L, Wu L X, Zhang R H, Qin J X 2019 Acta Phys. Sin. 68 014301
Google Scholar
[13] 杨帆, 王华, 高文典, 孟小嵩, 刘云龙 2021 海洋预报 38 103
Google Scholar
Yang F, Wang H, Gao W D, Meng X S, Liu Y L 2021 Marine Forecasts. 38 103
Google Scholar
[14] Henrick R F, Burkom H S 1983 J. Acoust. Soc. Am. 73 173
Google Scholar
[15] Lawrence M W 1983 J. Acoust. Soc. Am. 73 474
Google Scholar
[16] Baer R N 1981 J. Acoust. Soc. Am. 69 70
Google Scholar
[17] 毕思昭, 彭朝晖 2021 70 114303
Google Scholar
Bi S Z, Peng Z H 2021 Acta Phys. Sin. 70 114303
Google Scholar
[18] Guthrie A N, Fitzgerald R M, Nutile D A, Shaffer J D 1974 J. Acoust. Soc. Am. 56 58
Google Scholar
[19] 张海刚, 马志康, 付金山, 朴胜春 2021 声学学报 46 1093
Google Scholar
Zhang H G, Ma Z K, Fu J S, Piao S C 2021 Acta Acust. 46 1093
Google Scholar
[20] Davis J A 1975 J. Acoust. Soc. Am. 57 276
Google Scholar
[21] Tindle C T, Guthrie K M 1974 J. Sound Vibration. 34 291
Google Scholar
[22] Guthrie K M 1974 J. Sound Vibration. 32 289
Google Scholar
[23] Gordon D F 1980 J. Acoust. Soc. Am. 67 106
Google Scholar
[24] Tindle C T, Weston D E 1980 J. Acoust. Soc. Am. 67 1614
Google Scholar
[25] Tindle C T, Bold G E J 1981 J. Acoust. Soc. Am. 70 813
Google Scholar
[26] 张仁和, 李风华 1999 中国科学 A辑 29 241
Zhang R H, Li F H 1999 Sci. China A 29 241 (in Chinese)
[27] Murphy E L, Davis J A 1974 J. Acoust. Soc. Am. 56 1747
Google Scholar
[28] Davis J A 1974 Modified Ray Theory for Discontinuous Media (Massachusetts: Woods Hole Institution) p18
[29] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (2nd Ed.) (NewYork: Springer-Verlag) pp86, 219, 340
[30] 张揽月, 张明辉 2016 振动与声基础 (哈尔滨: 哈尔滨工程大学出版社) 第95页
Zhang L Y, Zhang M H 2016 Foundation of Vibration and Sound (Harbin: Harbin Engineering University Press) p95 (in Chinese)
[31] Chapman D M F, Ellis D D 1983 J. Acoust. Soc. Am. 74 973
Google Scholar
[32] Ferla M C, Jensen F B, Kuperman W A 1982 J. Acoust. Soc. Am. 72 505
Google Scholar
[33] Tindle C T 2002 J. Acoust. Soc. Am. 112 464
Google Scholar
[34] White D W, Pedersen M A 1981 J. Acoust. Soc. Am. 69 1029
Google Scholar
[35] Grigorieva N S, Fridman G M, Mercer J A, et al. 2009 J. Acoust. Soc. Am. 125 1919
Google Scholar
-
图 1 Munk声速剖面
Figure 1. Munk sound speed profile.
图 2 不同频率下的本征函数与声线轨迹示意图 (a) 30 Hz时的RR型模态; (b) 100 Hz时的RR型模态; (c) 与本征函数对应的声线轨迹
Figure 2. Eigenfunctions at different frequencies and schematic diagram of a sound ray trace: (a) RR mode at 30 Hz; (b) RR mode at 100 Hz; (c) a ray corresponding to the eigenfunction.
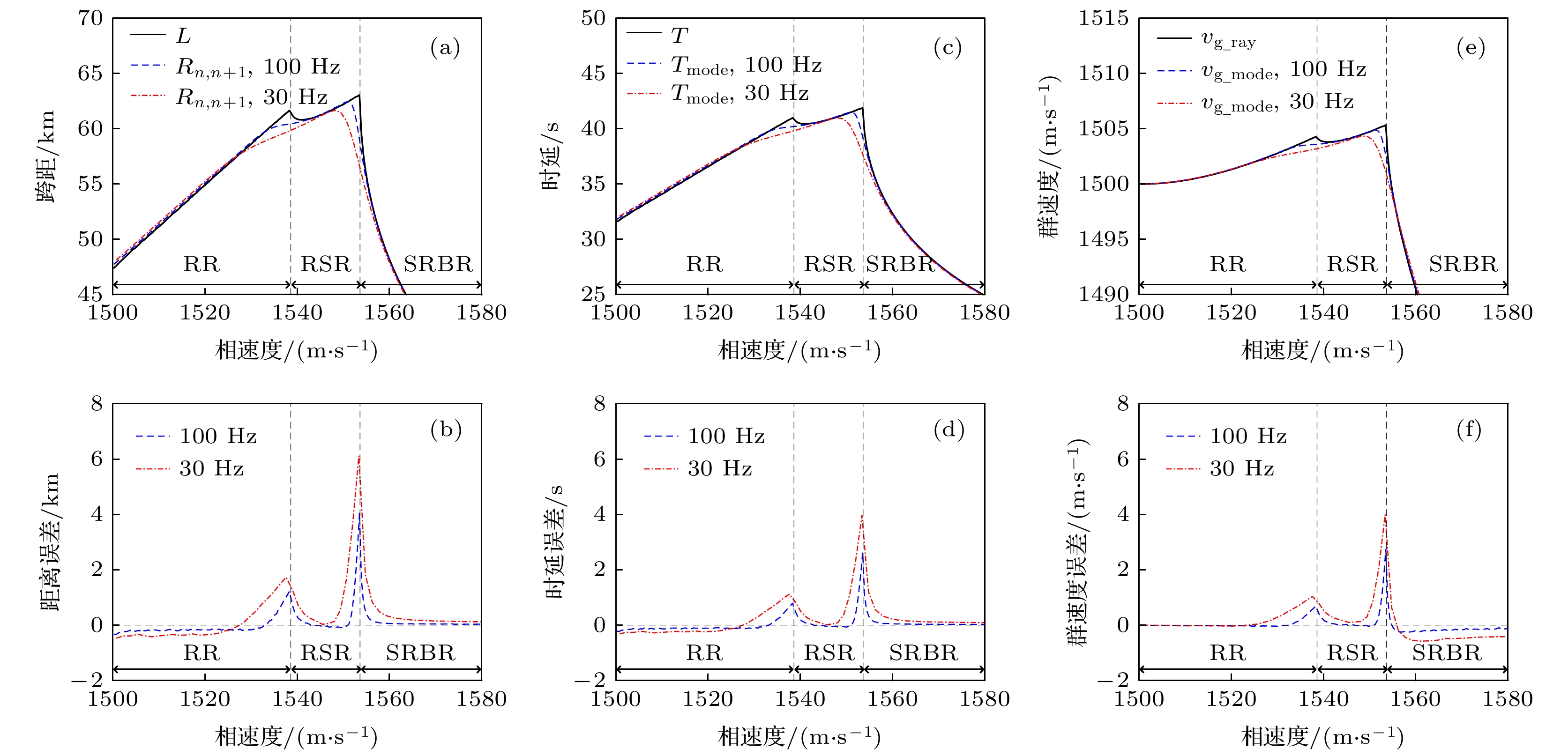
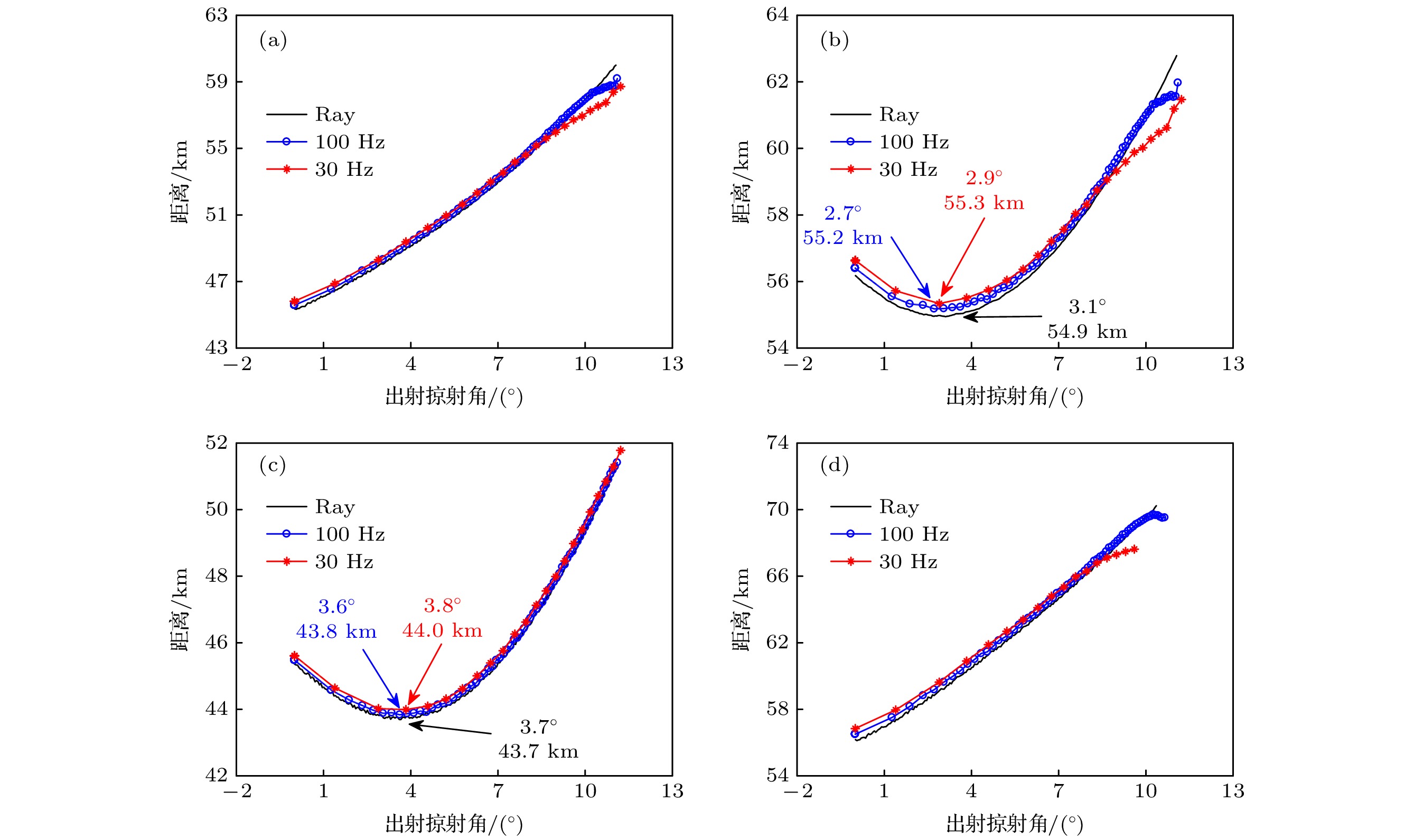
图 3 不同频率下经典射线理论与简正波理论的计算结果以及经典射线理论的计算误差 (a) 声线跨距; (b) 距离误差; (c) 传播时延; (d) 传播时延误差; (e) 群速度; (f) 群速度误差
Figure 3. Calculation results of classical ray theory and normal mode theory at different frequencies and the calculation errors of classical ray theory: (a) Ray skip distance; (b) distance error; (c) traveling time; (d) traveling time error; (e) group velocity; (f) group velocity error.
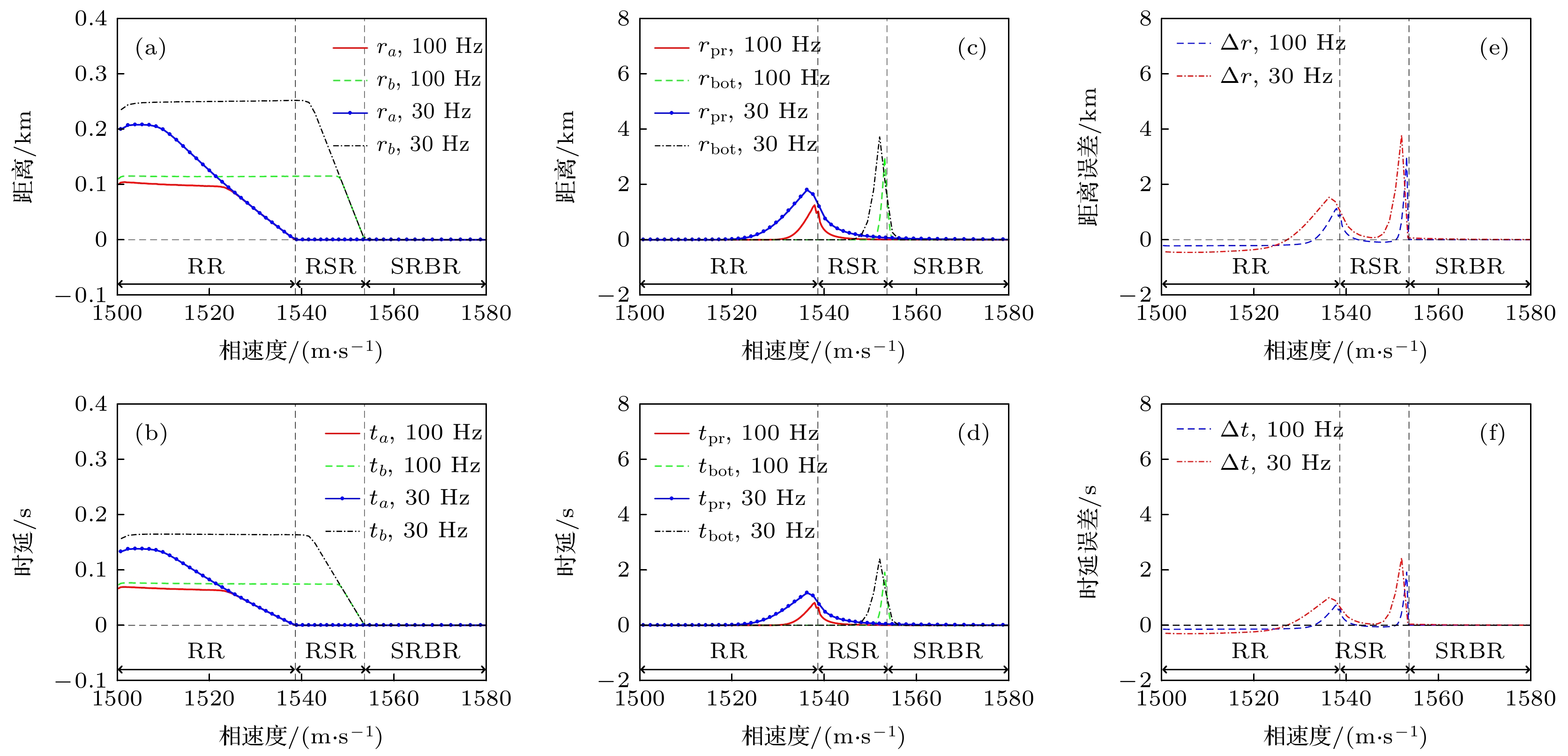
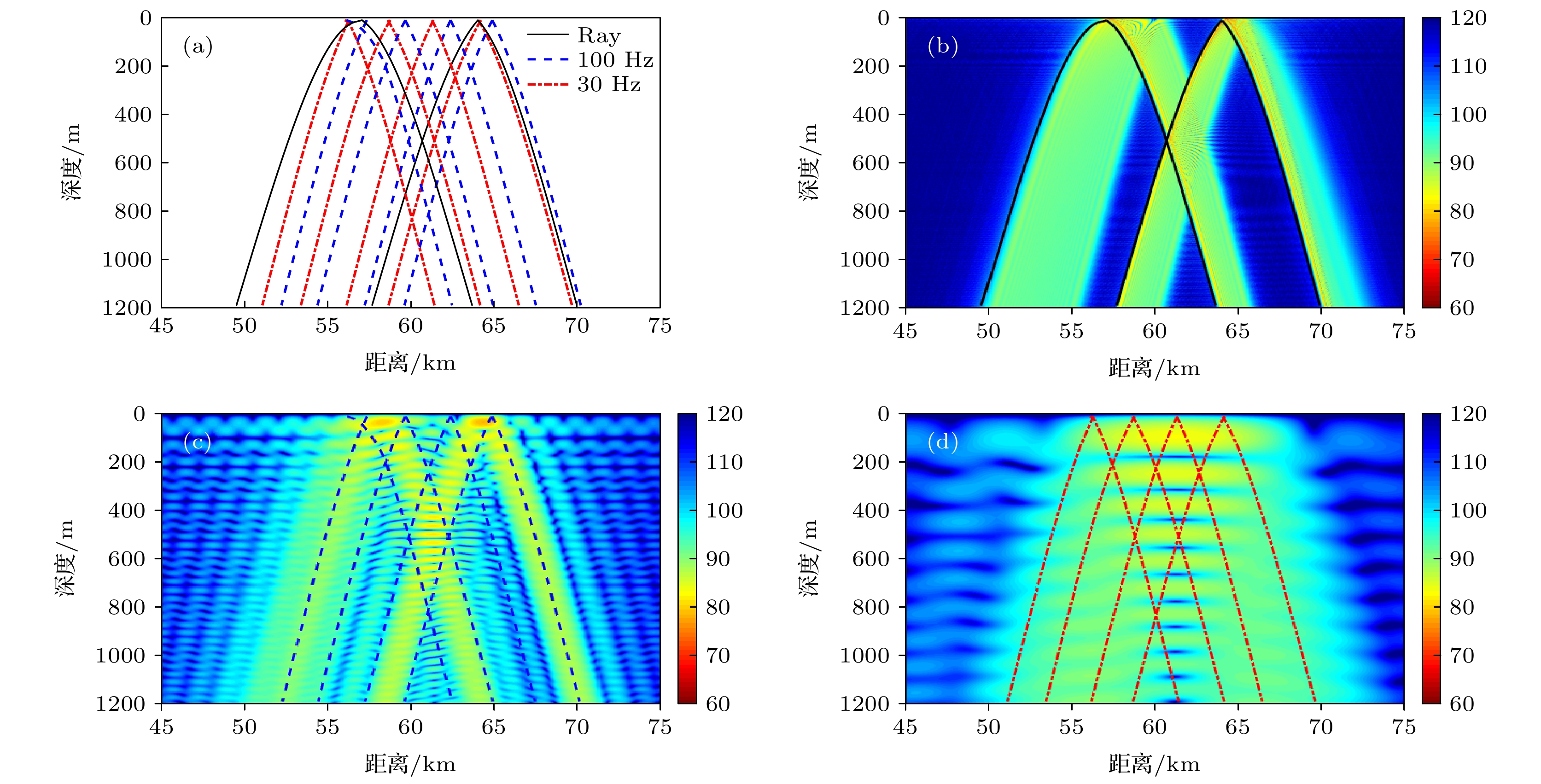
图 4 不同频率下声衍射对距离与时延的贡献 (a)
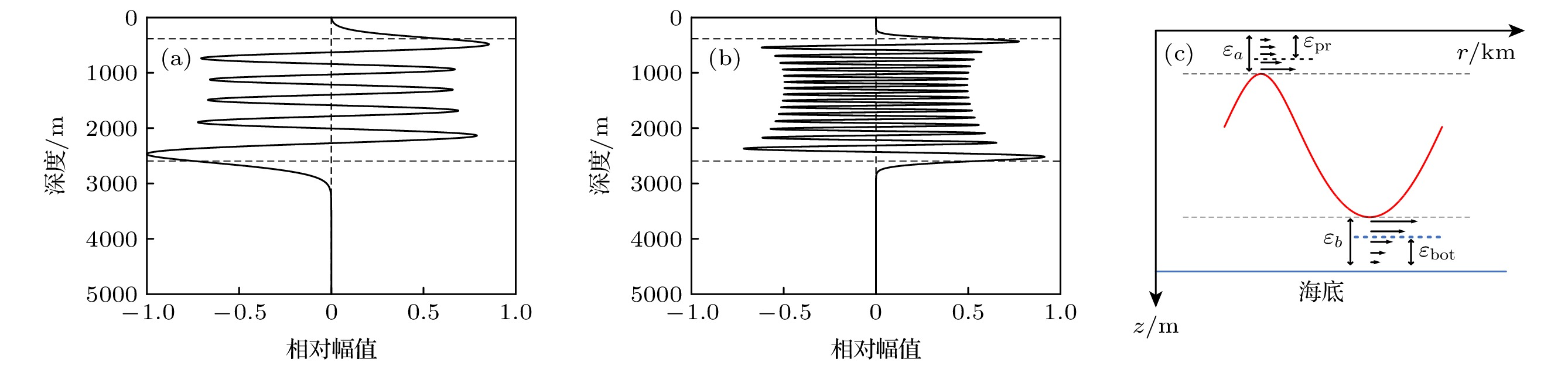
${\phi _a}$ 与${\phi _b}$ 对传播距离的贡献; (b)${\phi _a}$ 与${\phi _b}$ 对传播时延的贡献; (c)${\phi _{{\text{pr}}}}$ 与${\phi _{{\text{bot}}}}$ 对传播距离的贡献; (d)${\phi _{{\text{pr}}}}$ 与${\phi _{{\text{bot}}}}$ 对传播时延的贡献; (e)$\Delta r$ ; (f)$\Delta t$ Figure 4. Contribution of sound diffraction to propagation distance and traveling time at different frequencies: (a) Contribution of
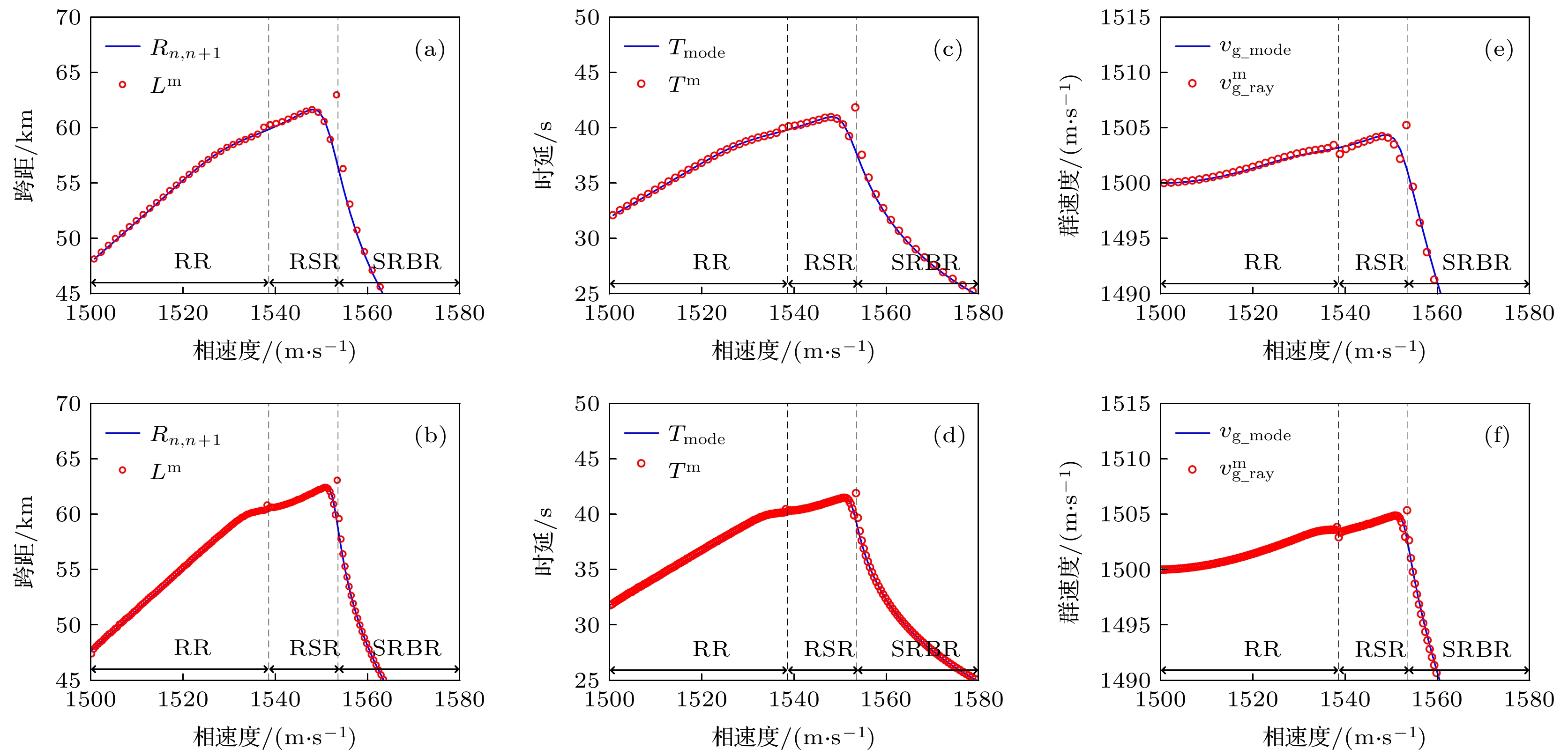
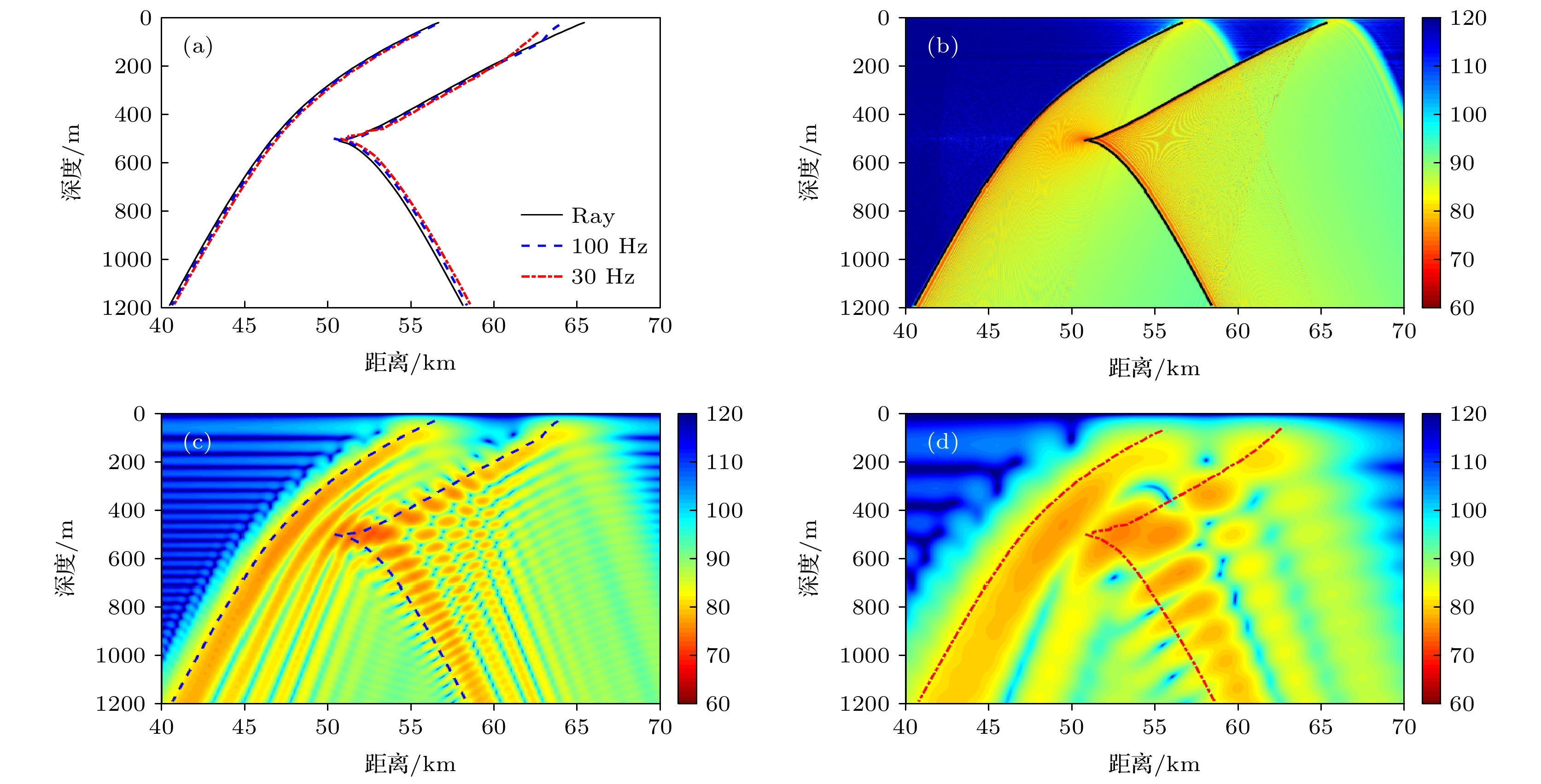
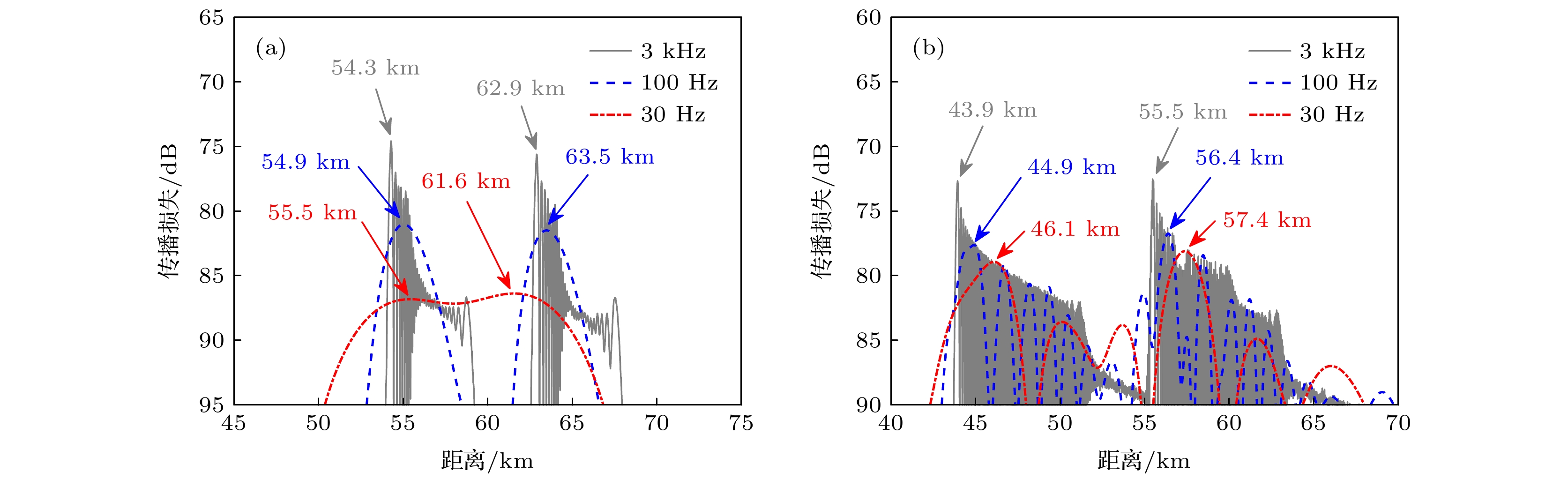
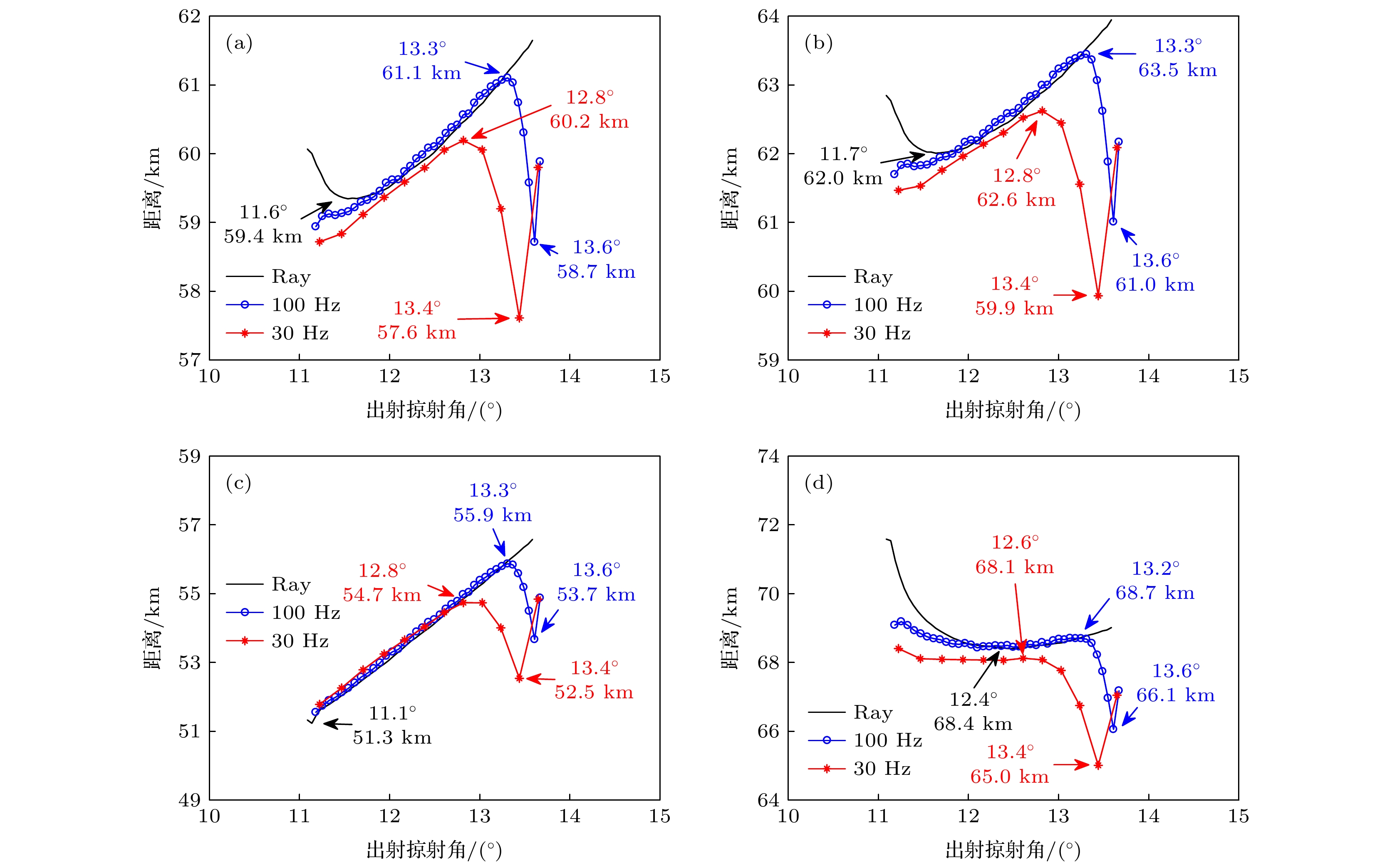
${\phi _a}$ and${\phi _b}$ to propagation distance; (b) contribution of${\phi _a}$ and${\phi _b}$ to traveling time; (c) contribution of${\phi _{{\text{pr}}}}$ and${\phi _{{\text{bot}}}}$ to propagation distance; (d) contribution of${\phi _{{\text{pr}}}}$ and${\phi _{{\text{bot}}}}$ to traveling time; (e)$\Delta r$ ; (f)$\Delta t$ .
图 5 不同频率下利用衍射相移对声场参数的修正结果 (a) 30 Hz时的声线跨距; (b) 100 Hz时的声线跨距; (c) 30 Hz时的传播时延; (d) 100 Hz时的传播时延; (e) 30 Hz时的群速度; (f) 100 Hz时的群速度
Figure 5. Correction results of sound field parameters by diffraction phase shift at different frequencies: (a) Ray skip distance at 30 Hz; (b) ray skip distance at 100 Hz; (c) traveling time at 30 Hz; (d) traveling time at 100 Hz; (e) group velocity at 30 Hz; (f) group velocity at 100 Hz.
图 6 声源深度500 m, 接收深度1000 m时的四类折射声线示意图 (a) r1; (b) r2; (c) r3; (d) r4
Figure 6. Schematic diagram of four types of refracted rays where source depth is 500 m and receiver depth is 1000 m: (a) r1; (b) r2; (c) r3; (d) r4.
图 7 声源深度500 m, 接收深度800 m时不同频率下RR型声线在不同出射掠射角下的水平距离 (a) r1; (b) r2; (c) r3; (d) r4
Figure 7. The horizontal distance of RR rays under different initial grazing angles at different frequencies when sound source depth is 500 m and the receiver depth is 800 m: (a) r1; (b) r2; (c) r3; (d) r4
图 8 声源深度500 m (a)不同频率下RR型会聚区的焦散线; (b) 3 kHz时的传播损失; (c) 100 Hz时的传播损失; (d) 30 Hz时的传播损失
Figure 8. Source depth is 500 m: (a) RR caustics at different frequencies; (b) transmission loss at 3 kHz; (c) transmission loss at 100 Hz; (d) transmission loss at 30 Hz.
图 9 声源深度500 m时不同频率下RR型会聚区的传播损失 (a) 接收深度100 m; (b)接收深度800 m
Figure 9. Transmission loss curves of RR convergence zones at different frequencies when source depth is 500 m: (a) Receiver depth is 100 m; (b) receiver depth is 800 m.
图 10 声源深度500 m, 接收深度800 m时不同频率下RSR型声线在不同出射掠射角下的水平距离 (a) r1; (b) r2; (c) r3; (d) r4
Figure 10. The horizontal distance of RSR rays under different initial grazing angles at different frequencies when sound source depth is 500 m and the receiver depth is 800 m: (a) r1; (b) r2; (c) r3; (d) r4.
图 11 声源深度500 m (a)不同频率下RSR型会聚区的焦散线; (b) 3 kHz时的传播损失; (c) 100 Hz时的传播损失; (d) 30 Hz时的传播损失
Figure 11. At the source depth of 500 m: (a) RSR caustics at different frequencies; (b) transmission loss at 3 kHz; (c) transmission loss at 100 Hz; (d) transmission loss at 30 Hz.
图 12 声源深度500 m, 接收深度800 m时不同频率下RSR型会聚区的传播损失
Figure 12. Transmission loss curves of RSR convergence zones at different frequencies when source depth is 500 m and receiver depth is 800 m.
表 1 不同频率下, 不同相速度区间内
${r_a}$ ,${r_b}$ ,${r_{{\text{pr}}}}$ ,${r_{{\text{bot}}}}$ 与$\Delta r$ 的取值符号Table 1. Values of
${r_a}$ ,${r_b}$ ,${r_{{\text{pr}}}}$ ,${r_{{\text{bot}}}}$ and$\Delta r$ in different phase velocity range at different frequencies.相速度区间/(m·s–1) ${r_a}$ ${r_b}$ ${r_{{\text{pr}}}}$ ${r_{{\text{bot}}}}$ $\Delta r$ 30 Hz 100 Hz 1500—1519 1500—1530 > 0 > 0 0 0 < 0 1519—1527 1530—1533 > 0 > 0 > 0 0 < 0 1527.0—1538.6 1533.0—1538.6 > 0 > 0 > 0 0 > 0 1538.6—1544.0 1538.6—1543.0 0 > 0 > 0 0 > 0 — 1543—1550 0 > 0 > 0 0 < 0 — 1550—1551 0 > 0 > 0 > 0 < 0 1544.0—1553.6 1551.0—1553.6 0 > 0 > 0 > 0 > 0 1553.6—1556.0 1553.6—1555.0 0 0 > 0 > 0 > 0 1556—1568 1555—1556 0 0 > 0 0 > 0 1568—1700 1556—1700 0 0 0 0 0 
DownLoad: CSV
-
[1] Munk W H 1974 J. Acoust. Soc. Am. 55 220
Google Scholar
[2] Hale F E 1961 J. Acoust. Soc. Am. 33 456
Google Scholar
[3] Brekhovskih L M 1980 Waves in Layered Media (2nd Ed.) (New York: Academic Press) p377
[4] Urick R J 1965 J. Acoust. Soc. Am. 38 348
Google Scholar
[5] 张仁和 1980 声学学报 1 28
Google Scholar
Zhang R H 1980 Acta Acust. 1 28
Google Scholar
[6] 张仁和 1982 声学学报 7 75
Google Scholar
Zhang R H 1982 Acta Acust. 7 75
Google Scholar
[7] 张仁和 1988 声学学报 13 101
Google Scholar
Zhang R H 1988 Acta Acust. 13 101
Google Scholar
[8] Bongiovanni K P, Siegmann W L 1996 J. Acoust. Soc. Am. 100 3033
Google Scholar
[9] 徐传秀 2017 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Xu C X 2017 Ph. D. Dissertation (Harbin: Harbin Engineering University) (in Chinese)
[10] 朴胜春, 栗子洋, 王笑寒, 张明辉 2021 70 024301
Google Scholar
Piao S C, Li Z Y, Wang X H, Zhang M H 2021 Acta Phys. Sin. 70 024301
Google Scholar
[11] 张青青, 李整林, 秦继兴, 李文, 吴双林 2020 声学学报 45 458
Google Scholar
Zhang Q Q, Li Z L, Qin J X, Li W, Wu S L 2020 Acta Acust. 45 458
Google Scholar
[12] 张鹏, 李整林, 吴立新, 张仁和, 秦继兴 2019 68 014301
Google Scholar
Zhang P, Li Z L, Wu L X, Zhang R H, Qin J X 2019 Acta Phys. Sin. 68 014301
Google Scholar
[13] 杨帆, 王华, 高文典, 孟小嵩, 刘云龙 2021 海洋预报 38 103
Google Scholar
Yang F, Wang H, Gao W D, Meng X S, Liu Y L 2021 Marine Forecasts. 38 103
Google Scholar
[14] Henrick R F, Burkom H S 1983 J. Acoust. Soc. Am. 73 173
Google Scholar
[15] Lawrence M W 1983 J. Acoust. Soc. Am. 73 474
Google Scholar
[16] Baer R N 1981 J. Acoust. Soc. Am. 69 70
Google Scholar
[17] 毕思昭, 彭朝晖 2021 70 114303
Google Scholar
Bi S Z, Peng Z H 2021 Acta Phys. Sin. 70 114303
Google Scholar
[18] Guthrie A N, Fitzgerald R M, Nutile D A, Shaffer J D 1974 J. Acoust. Soc. Am. 56 58
Google Scholar
[19] 张海刚, 马志康, 付金山, 朴胜春 2021 声学学报 46 1093
Google Scholar
Zhang H G, Ma Z K, Fu J S, Piao S C 2021 Acta Acust. 46 1093
Google Scholar
[20] Davis J A 1975 J. Acoust. Soc. Am. 57 276
Google Scholar
[21] Tindle C T, Guthrie K M 1974 J. Sound Vibration. 34 291
Google Scholar
[22] Guthrie K M 1974 J. Sound Vibration. 32 289
Google Scholar
[23] Gordon D F 1980 J. Acoust. Soc. Am. 67 106
Google Scholar
[24] Tindle C T, Weston D E 1980 J. Acoust. Soc. Am. 67 1614
Google Scholar
[25] Tindle C T, Bold G E J 1981 J. Acoust. Soc. Am. 70 813
Google Scholar
[26] 张仁和, 李风华 1999 中国科学 A辑 29 241
Zhang R H, Li F H 1999 Sci. China A 29 241 (in Chinese)
[27] Murphy E L, Davis J A 1974 J. Acoust. Soc. Am. 56 1747
Google Scholar
[28] Davis J A 1974 Modified Ray Theory for Discontinuous Media (Massachusetts: Woods Hole Institution) p18
[29] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (2nd Ed.) (NewYork: Springer-Verlag) pp86, 219, 340
[30] 张揽月, 张明辉 2016 振动与声基础 (哈尔滨: 哈尔滨工程大学出版社) 第95页
Zhang L Y, Zhang M H 2016 Foundation of Vibration and Sound (Harbin: Harbin Engineering University Press) p95 (in Chinese)
[31] Chapman D M F, Ellis D D 1983 J. Acoust. Soc. Am. 74 973
Google Scholar
[32] Ferla M C, Jensen F B, Kuperman W A 1982 J. Acoust. Soc. Am. 72 505
Google Scholar
[33] Tindle C T 2002 J. Acoust. Soc. Am. 112 464
Google Scholar
[34] White D W, Pedersen M A 1981 J. Acoust. Soc. Am. 69 1029
Google Scholar
[35] Grigorieva N S, Fridman G M, Mercer J A, et al. 2009 J. Acoust. Soc. Am. 125 1919
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3817
- PDF Downloads: 82
- Cited By: 0
