-
Convergence-zone (CZ) sound propagation is one of the most important hydro-acoustic phenomena in the deep ocean, which allows the acoustic signals with high intensity and low distortion to realize the long-range transmission. Accurate prediction and identification of CZ is of great significance in implementing remote detection or communication, but there is still no standard definition in the sense of mathematical physics for convergence zone. Especially for the issue of systematic error of computation introduced by the earth curvature, there is no exact propagation model. The curvature-correction methods always lead to the imprecision of the ray phase. In previous research work, we realized that the Riemannian geometric meaning of the caustics phenomena caused by ray convergence is that the caustic points are equivalent to the conjugate points, which form on geodesics with positive section curvature. In this work, we present a spherical layered acoustic ray propagation model for CZ based on the Riemannian geometric theory. With direct computation in the curved manifolds of the earth , a Riemannian geometric description of CZ is provided for the first time, on the basis of comprehensive analysis about its characteristics. And it shows that the mathematical expression of section curvature adds an additional item
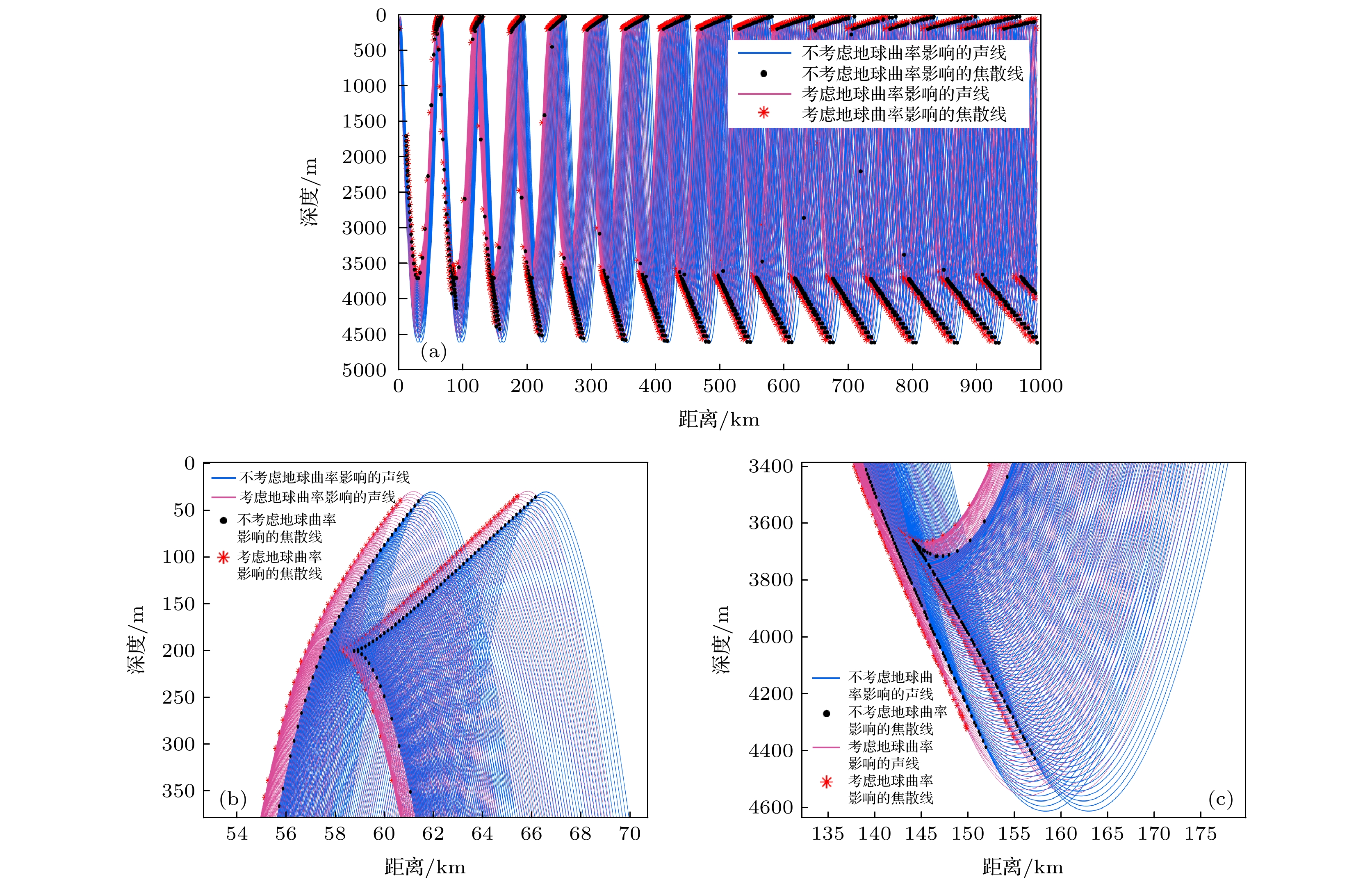
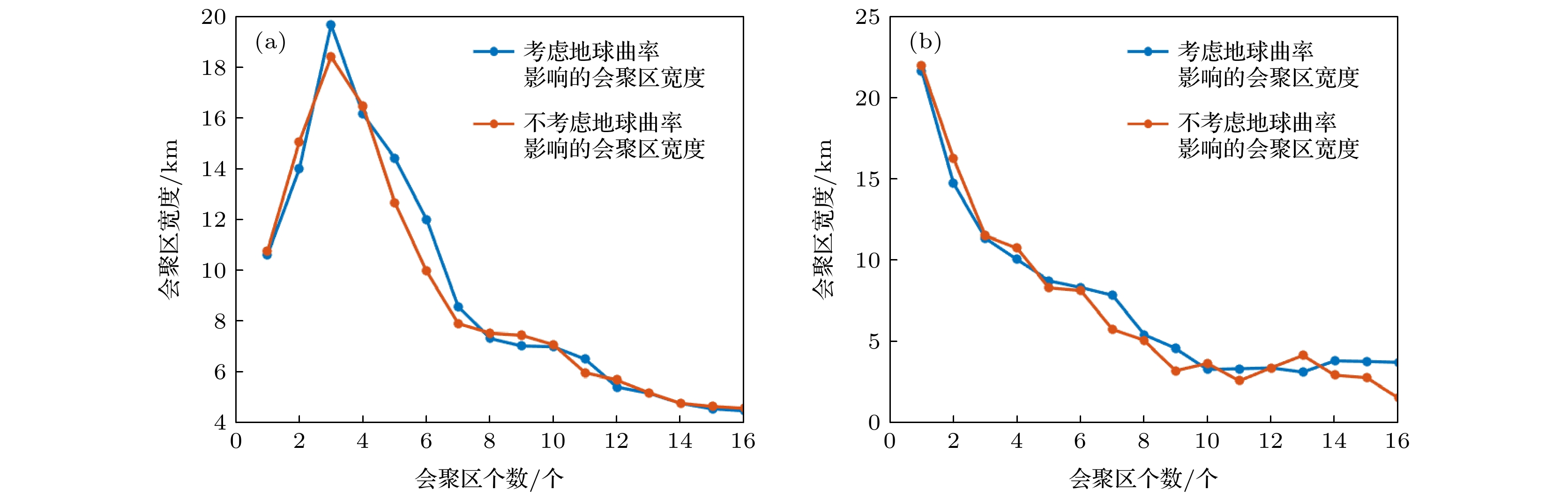
${{\hat c(l){{\hat c}^\prime }(l)}}/{l}$ after considering the earth curvature, which reflects the influence of the earth curvature on the ray topology and CZ. By means of Jacobi field theory of Riemannian geometry, computational rule and method of the location and distance of CZ in deep water are proposed. Taking the typical Munk sound velocity profile for example, the new Riemannian geometric model of CZ is compared with the normal mode and curvature-correction method. Simulation and analysis show that the Riemannian geometric model of CZ given in this paper is a mathematical form naturally considering the earth curvature with theoretical accuracy, which lays more solid scientific foundations for the study of convergence zone. Moreover, we find that the location of CZ moves towards sound source when the earth curvature is considered, and the width of CZ near the sea surface first increases and then decreases with sound propagation proceeding. The maximum width is about 20 km and the minimum is about 4 km.-
Keywords:
- earth curvature /
- Jacobi field /
- sound propagation in deep ocean /
- ray model /
- convergence zone
[1] Jensen F B, Kuperman W A, Porter M B 2011 Schmidt H Computational Ocean Acoustics ( NewYork: Springer-Verlag) p125
[2] Hale F E 1961 J. Acoust. Soc. Am. 33 456
Google Scholar
[3] Urick R J 1965 J. Acoust. Soc. Am. 38 348
[4] 朴胜春, 栗子洋, 王笑寒, 张明辉 2021 70 024301
Google Scholar
Piao S C, Li Z Y, Wang X H, Zhang M H 2021 Acta Phys. Sin. 70 024301
Google Scholar
[5] 李文, 李整林 2016 中国科学: 物理学 力学 天文学 46 094303
Google Scholar
Li W, Li Z L 2016 Sci. Sin. Phys. Mech. Astron. 46 094303
Google Scholar
[6] 张仁和 1982 声学学报 7 75
Google Scholar
Zhang R H 1982 Acta Acust 7 75
Google Scholar
[7] 张仁和 1980 声学学报 1 28
Zhang R H 1980 Acta Acust 1 28
[8] Bongiovanni K P, Siegmann W L, Ko D S 1996 J. Acoust. Soc. Am. 100 3033
Google Scholar
[9] Tolstoy I, Clay C S 1987 Ocean Acoustics: Theory and Experiment in Underwater Sound (New York: American Institute of Physics) p20
[10] Wu S L, Li Z L, Qin J X, Wang M Y, Li W 2022 J. Mar. Sci. Eng. 10 424
Google Scholar
[11] 庄益夫, 张旭, 刘艳 2013 海洋通报 32 45
Google Scholar
Zhuang Y F, Zhang X, Liu Y 2013 Mar. Sci. Bull. 32 45
Google Scholar
[12] 张晶晶, 罗博 2017 声学与电子工程 2017 8
Zhang J J, Luo B 2017 Acoust. Electron. Eng. 2017 8
[13] Yang Y, Guo L H, Gong Z X 2020 Global Oceans 2020: Singapore–U. S. Gulf Coast Electr Network, October 5–30, 2021 p2021-10-08
[14] 龚敏, 肖金泉, 王孟新, 吴寅庚, 黄德华 1987 声学学报 12 417
Google Scholar
Gong M, Xiao J Q, Wang M X, Wu Y G, Huang D H 1987 Acta Acust. 12 417
Google Scholar
[15] Vadov R A 2005 Acoust. Phys. 51 265
Google Scholar
[16] 徐传秀, 朴胜春, 张红星, 杨士莪, 张海刚, 周建波 2015 声学技术 34 79
Xu C X, Piao S C, Zhang H X, Yang S E, Zhang H G, Zhou J B 2015 Tech. Acoust. 34 79
[17] 毕思昭, 彭朝晖 2021 70 114303
Google Scholar
Bi S Z, Peng Z H 2021 Acta Phys. Sin. 70 114303
Google Scholar
[18] Munk W H, O'Reilly W C, Reid J L 1988 J. Phys. Oceanogr. 18 1876
Google Scholar
[19] Yan J, Kang K Y 1995 Appl. Acoust. 45 9
Google Scholar
[20] Yan J 1999 Appl. Acoust. 57 163
Google Scholar
[21] 郭肖晋, 马树青, 张理论, 蓝强, 黄创霞 2022 72 044302
Google Scholar
[22] 陈维恒, 李兴校 2002 黎曼几何引论 (北京: 北京大学出版社 第267页
Chen W H, Li X X 2002 Introduction to Riemannian Geometry (Beijing: Peking University Press) p267 (in Chinese)
[23] 刘伯胜, 雷家煜 2010 水声学原理 (哈尔滨: 哈尔滨工程大学出版社) 第77页
Liu B S, Lei J Y 2010 Principles of Underwater Acoustics (Harbin: Harbin Engineering University Press) p77 (in Chinese)
[24] Cheeger J, Ebin D G 2008 Comparison Theorems in Riemannian Geometry (Providence, Rhode Island: American Mathematical Society) p35
-
图 1 考虑地球曲率后的声传播 (a) 对称截面; (b)
$ (l, \theta ) $ 平面上的雅可比场几何示意图Figure 1. Sound propagation considering the earth curvature: (a) Symmetrical section; (b) geometric structure of Jacobi field.
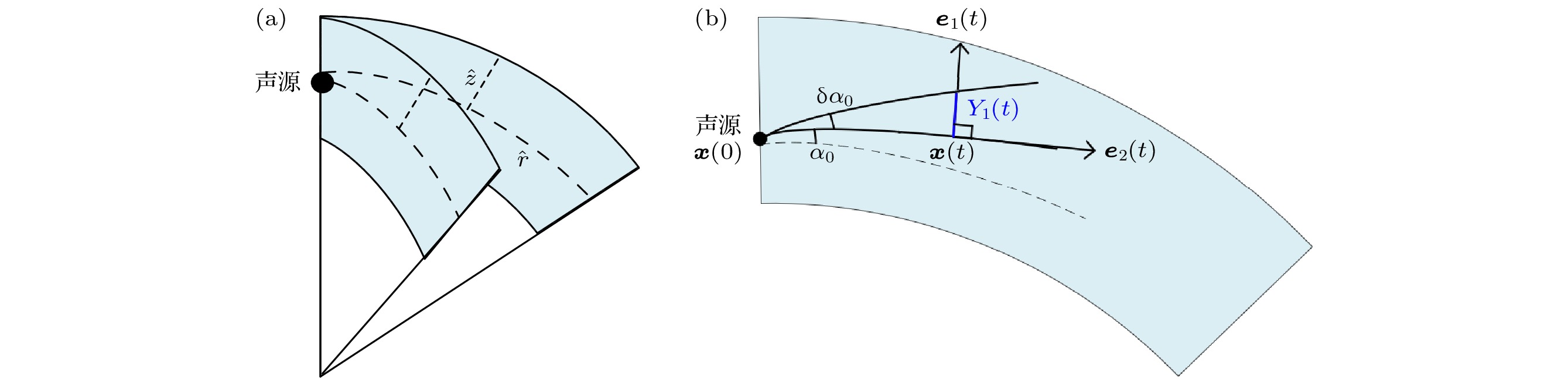
图 2 考虑地球曲率前后所选声线的截面曲率 (a) 660 s内50根声线的截面曲率; (b) 入射角
${\alpha _0}{\text{ = }}{0^\circ }$ 的声线形成第一个焦散点前的截面曲率Figure 2. Section curvature before and after considering the earth curvature: (a) Section curvature of 50 sound lines in 660 s; (b) section curvature of sound line with elevation angle
${\alpha _0}{\text{ = }}{0^\circ }$ before forming the first caustic.
图 3 660 s内所选50根声线的雅可比场
$ {Y_1}(t) $ Figure 3. Jacobi field
$ {Y_1}(t) $ of 50 sound lines in 660 s.
图 4 弯曲声道中的声线、会聚区和焦散点 (a) 全图; (b) 细节图
Figure 4. Ray, convergence zone and caustics in curved sound channel: (a) Full picture; (b) details picture.
图 5 考虑地球曲率前后的声线和焦散线 (a) 全图; (b) 上反转点焦散线; (c) 下反转点焦散线
Figure 5. Rays and caustics before and after considering the earth curvature: (a) Full picture; (b) upper turning point caustics; (c) lower turning point caustics.
图 6 考虑地球曲率前后的声线和会聚区
Figure 6. Rays and convergence zones before and after considering the earth curvature.
图 7 考虑地球曲率后会聚区偏移的距离
Figure 7. Movement of the convergence zone after considering the earth curvature.
图 8 不同接收深度处考虑地球曲率和不考虑地球曲率的会聚区宽度 (a) 200 m; (b) 4000 m
Figure 8. The width of convergence zone considering and not considering earth curvature at the two different receiver depths: (a) 200 m; (b) 4000 m.
图 9 不同几何扩展损失阈值下的会聚区 (a)
$ \beta = 25 $ dB; (b)$ \beta = 15 $ dBFigure 9. Convergence zones at two different geometric spread loss thresholds
$ \beta $ : (a)$ \beta = 25 $ dB; (b)$ \beta = 15 $ dB.
图 10 不同声源深度的焦散点与会聚区 (a) 150 m; (b) 300 m
Figure 10. Convergence zones at two different source depths: (a) 150 m; (b) 300 m.
图 11 黎曼几何与简正波法计算的会聚区对比图 (a) 黎曼几何理论计算的会聚区 (b) 简正波法(Kraken软件)计算的会聚区
Figure 11. The convergence zones by Riemann-Geometry and Normal-Mode theory: (a) Based on Riemann-Geometry Theory ; (b) based on Normal-Modes (Kraken).
表 1 考虑地球曲率前后Munk声速剖面下截面曲率对比
Table 1. Comparison of sectional curvature of Munk sound speed profile.
$ K \gt 0 $ $ K = 0 $ $ K \lt 0 $ $ {K_{\max }} $ 考虑地球曲率 $ \hat z \lt 4519 $ m $ \hat z = 4519 $ m $ \hat z \gt 4519 $ m 0.2878 不考虑地球曲率 $ z \lt 4510 $ m $ z = 4510 $ m $ z \gt 4510 $ m 0.2877 
DownLoad: CSV
表 2 考虑地球曲率后会聚区向声源方向前移距离
Table 2. Distance of convergence zone moving forward towards sound source after considering the earth curvature.
第4个会聚区 第9个会聚区 第16个会聚区 上反转点会聚区前移距离/km 2.5 5.5 9.6 下反转点会聚区前移距离/km 2.3 5.4 9.7
DownLoad: CSV
-
[1] Jensen F B, Kuperman W A, Porter M B 2011 Schmidt H Computational Ocean Acoustics ( NewYork: Springer-Verlag) p125
[2] Hale F E 1961 J. Acoust. Soc. Am. 33 456
Google Scholar
[3] Urick R J 1965 J. Acoust. Soc. Am. 38 348
[4] 朴胜春, 栗子洋, 王笑寒, 张明辉 2021 70 024301
Google Scholar
Piao S C, Li Z Y, Wang X H, Zhang M H 2021 Acta Phys. Sin. 70 024301
Google Scholar
[5] 李文, 李整林 2016 中国科学: 物理学 力学 天文学 46 094303
Google Scholar
Li W, Li Z L 2016 Sci. Sin. Phys. Mech. Astron. 46 094303
Google Scholar
[6] 张仁和 1982 声学学报 7 75
Google Scholar
Zhang R H 1982 Acta Acust 7 75
Google Scholar
[7] 张仁和 1980 声学学报 1 28
Zhang R H 1980 Acta Acust 1 28
[8] Bongiovanni K P, Siegmann W L, Ko D S 1996 J. Acoust. Soc. Am. 100 3033
Google Scholar
[9] Tolstoy I, Clay C S 1987 Ocean Acoustics: Theory and Experiment in Underwater Sound (New York: American Institute of Physics) p20
[10] Wu S L, Li Z L, Qin J X, Wang M Y, Li W 2022 J. Mar. Sci. Eng. 10 424
Google Scholar
[11] 庄益夫, 张旭, 刘艳 2013 海洋通报 32 45
Google Scholar
Zhuang Y F, Zhang X, Liu Y 2013 Mar. Sci. Bull. 32 45
Google Scholar
[12] 张晶晶, 罗博 2017 声学与电子工程 2017 8
Zhang J J, Luo B 2017 Acoust. Electron. Eng. 2017 8
[13] Yang Y, Guo L H, Gong Z X 2020 Global Oceans 2020: Singapore–U. S. Gulf Coast Electr Network, October 5–30, 2021 p2021-10-08
[14] 龚敏, 肖金泉, 王孟新, 吴寅庚, 黄德华 1987 声学学报 12 417
Google Scholar
Gong M, Xiao J Q, Wang M X, Wu Y G, Huang D H 1987 Acta Acust. 12 417
Google Scholar
[15] Vadov R A 2005 Acoust. Phys. 51 265
Google Scholar
[16] 徐传秀, 朴胜春, 张红星, 杨士莪, 张海刚, 周建波 2015 声学技术 34 79
Xu C X, Piao S C, Zhang H X, Yang S E, Zhang H G, Zhou J B 2015 Tech. Acoust. 34 79
[17] 毕思昭, 彭朝晖 2021 70 114303
Google Scholar
Bi S Z, Peng Z H 2021 Acta Phys. Sin. 70 114303
Google Scholar
[18] Munk W H, O'Reilly W C, Reid J L 1988 J. Phys. Oceanogr. 18 1876
Google Scholar
[19] Yan J, Kang K Y 1995 Appl. Acoust. 45 9
Google Scholar
[20] Yan J 1999 Appl. Acoust. 57 163
Google Scholar
[21] 郭肖晋, 马树青, 张理论, 蓝强, 黄创霞 2022 72 044302
Google Scholar
[22] 陈维恒, 李兴校 2002 黎曼几何引论 (北京: 北京大学出版社 第267页
Chen W H, Li X X 2002 Introduction to Riemannian Geometry (Beijing: Peking University Press) p267 (in Chinese)
[23] 刘伯胜, 雷家煜 2010 水声学原理 (哈尔滨: 哈尔滨工程大学出版社) 第77页
Liu B S, Lei J Y 2010 Principles of Underwater Acoustics (Harbin: Harbin Engineering University Press) p77 (in Chinese)
[24] Cheeger J, Ebin D G 2008 Comparison Theorems in Riemannian Geometry (Providence, Rhode Island: American Mathematical Society) p35
DownLoad:
Catalog
Metrics
- Abstract views: 4202
- PDF Downloads: 110
- Cited By: 0
