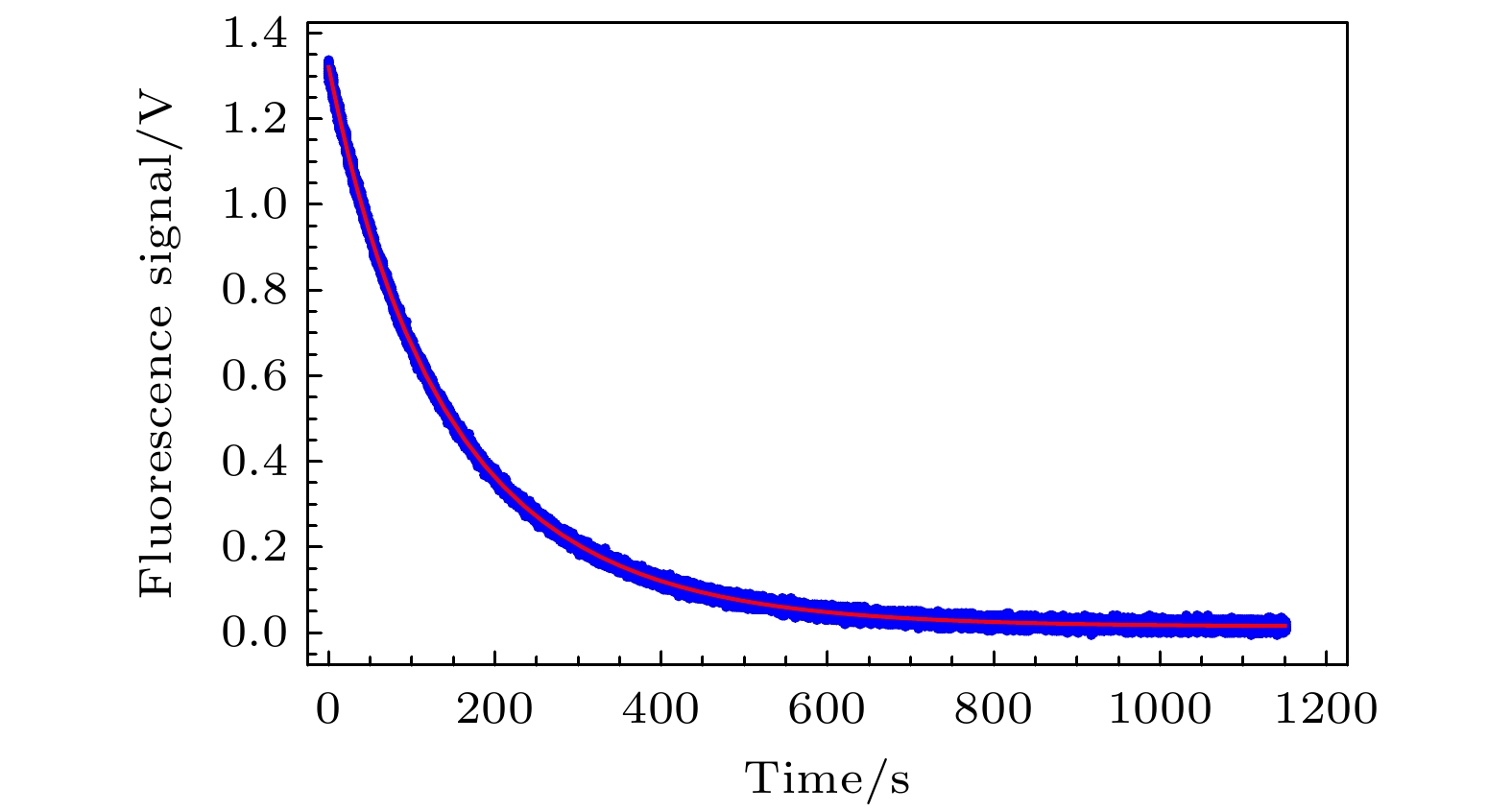
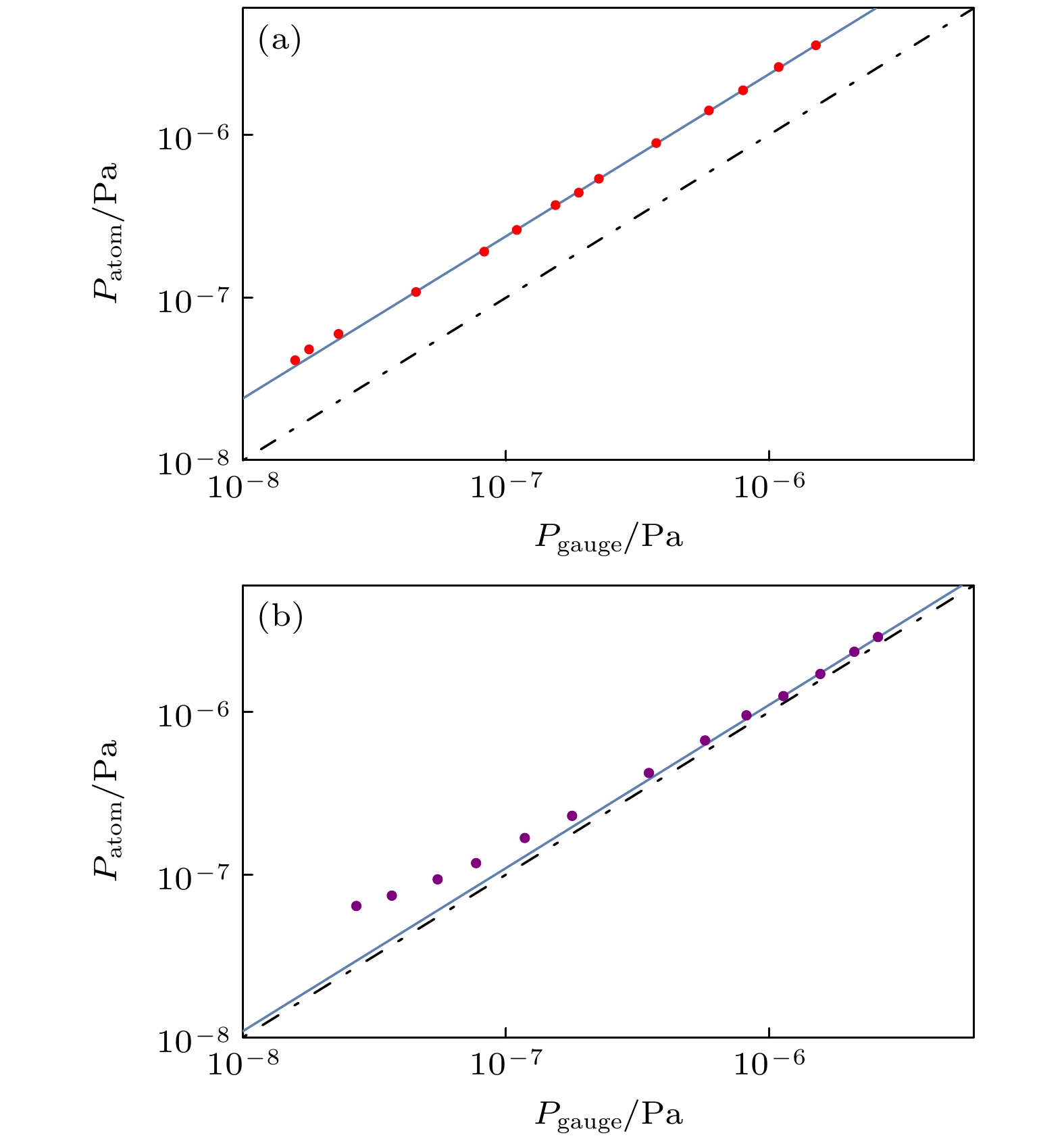
-
Ultra-high vacuum measurement and extremely high vacuum (UHV/XHV) measurement play an important role in high-tech fields such as deep space exploration, particle accelerators, and nanoscience; with the continuous extension of the lower limit of measurement, especially when it reaches the order of 10–10 Pa, higher requirements are placed on the accuracy of the measurement. At present, in the field of UHV/XHV measurement, ionization gauges based on the principle of neutral gas ionization are commonly applied to the vacuum measurement. However, traditional ionization vacuum gauges during use can create electronic excitation desorption effects, soft X-rays, and the effect of hot cathode outgassing, thereby affecting the accuracy of measurement and limiting the lower limit of measurement. Compared with the traditional measurement technology, this method uses the relationship between the loss rate and pressure caused by the collision of cold atoms trapped in the trap depth with the background gas to calculate the gas density and inversely calculate the vacuum pressure. Based on the intrinsic quantum mechanical properties of cold atom collisions, this method is expected to be developed into a new vacuum traceability standard. In this paper, based on the small-angle approximation and impulse approximation under the quantum scattering theory, the loss rate coefficient of the collision of 6Li cold atoms with background gas molecules is calculated. According to the ideal gas equation, the pressure inversion formula is obtained. The collision loss rate is extracted by accurately fitting the loss curve of the cold atom. In order to improve the accuracy of vacuum inversion and reduce the influence of quantum diffractive collision on loss rate measurement, the trap depth under the conditions of a certain cooling laser intensity, detuning, and magnetic field gradient is determined by the photoassociation method. Finally, in a range of 1 × 10–8–5 × 10–6 Pa, the inverted pressure value is compared with the measured value of the ionization meter, proving that this method has good accuracy and reliability in the inversion of vacuum pressure. At present, the main factor restricting the improvement of accuracy is the influence of the collision between the excited atoms in the magneto-optical trap and the background gas on the loss rate measurement. In the future, with the proportion of excited atoms and the excited state C6 coefficient to be precisely determined, the uncertainty of vacuum pressure measurement can be further reduced.
-
Keywords:
- vacuum pressure measurement /
- cold atoms /
- loss rate coefficient /
- trap depth
[1] Gibney E 2017 Nature 551 18
Google Scholar
[2] 范栋, 习振华, 贾文杰, 成永军, 李得天 2021 70 040602
Google Scholar
Fan D, Xi Z H, Jia W J, Cheng Y J, Li D T 2021 Acta Phys. Sin. 70 040602
Google Scholar
[3] Scherschligt J, Fedchak J A, Ahmed Z, Barker D S, Douglass K, Eckel S, Hanson E, Hendricks J, Klimov N, Purdy T, Ricker J, Singh R, Stone J 2018 J. Vac. Sci. Technol., A 36 040801
Google Scholar
[4] Calcatelli A 2013 Measurement 46 1029
Google Scholar
[5] 李得天, 成永军, 习振华 2018 宇航计测技术 38 1
Google Scholar
Li D T, Cheng Y J, Xi Z H 2018 J. Astronaut. Metrol. Meas. 38 1
Google Scholar
[6] Raab E L, Prentiss M, Cable A, Chu S, Pritchard D E 1987 Phys. Rev. Lett. 59 2631
Google Scholar
[7] Prentiss M, Cable A, Bjorkholm J E, Chu S, Raab E L 1988 Opt. Lett. 13 452
Google Scholar
[8] Bjorkholm J E 1988 Phys. Rev. A 38 1599
Google Scholar
[9] Arpornthip T, Sackett C A, Hughes K J 2012 Phys. Rev. A 85 033420
Google Scholar
[10] Yuan J P, Ji Z H, Zhao Y T, Chang X F, Xiao L T, Jia S T 2013 Appl. Opt. 52 6195
Google Scholar
[11] Xiang J F, Cheng H N, Peng X K, Wang X W, Ren W, Ji J W, Liu K K, Zhao J B, Li L, Qu Q Z, Li T, Wang B, Ye M F, Zhao X, Yao Y Y, Lü D S, Liu L 2018 Chin. Phys. B 27 073701
Google Scholar
[12] Scherschligt J, Fedchak J A, Barker D S, Eckel S, Klimov N, Makrides C, Tiesinga E 2017 Metrologia 54 125
Google Scholar
[13] Eckel S, Barker D S, Fedchak J A, Klimov N N, Norrgard E, Scherschligt J, Makrides C, Tiesinga E 2018 Metrologia 55 182
Google Scholar
[14] Barker D S, Klimov N N, Tiesinga E, Fedchak J A, Scherschligt J, Eckel S 2021 Measurement: Sensors 18 100229
[15] Makhalov V B, Martiyanov K A, Turlapov A V 2016 Metrologia 53 1287
Google Scholar
[16] Makhalov V B, Turlapov A V 2017 Quantum Electron. 47 431
Google Scholar
[17] Booth J L, Shen P R, Krems R V, Madison K W 2019 New J. Phys. 21 102001
Google Scholar
[18] Shen P R, Madison K W, Booth J L 2020 Metrologia 57 025015
Google Scholar
[19] Shen P R, Madison K W, Booth J L 2021 Metrologia 58 022101
Google Scholar
[20] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2019 Phys. Rev. A 99 042704
Google Scholar
[21] Bali S, O’Hara K M, Gehm M E, Granade S R, Thomas J E 1999 Phys. Rev. A 60 R29
Google Scholar
[22] Zhu C, Dalgarno A, Derevianko 2002 Phys. Rev. A 65 034708
Google Scholar
[23] 武跃龙, 李睿, 芮扬, 姜海峰, 武海斌 2018 67 163201
Google Scholar
Wu Y L, Li R, Rui Y, Jiang H F, Wu H B 2018 Acta Phys. Sin. 67 163201
Google Scholar
[24] Tiecke T G, Gensemer S D, Ludewig A, Walraven J T M 2009 Phys. Rev. A 80 013409
Google Scholar
[25] Hoffmann D, Bali S, Walker T 1996 Phys. Rev. A 54 1030
Google Scholar
[26] Dongen J V, Zhu C, Clement D, Dufour G, Booth J L, Madison K W 2011 Phys. Rev. A 84 022708
Google Scholar
[27] Hong S S, Shin Y H, Kim J T 2008 Measurement 41 1026
Google Scholar
[28] 李得天 2003 真空与低温 9 85
Google Scholar
Li D T 2003 Vac. Cryogenics 9 85
Google Scholar
-
图 1 测量系统示意图
Figure 1. Schematic diagram of measurement apparatus.
图 2 6Li原子的能级结构及光路设计示意图
Figure 2. Schematic diagram of energy level and optical path design of 6Li.
图 3 t = 0时刻关闭磁光阱装载后冷原子数的衰减曲线及拟合线
Figure 3. Decay curve of the number of cold atoms and corresponding fitting curve after switching off magneto optical trap (MOT) loading dynamics at time t = 0.
图 4 在3种不同催化激光失谐量Δ下K随占空比d的变化及线性拟合
Figure 4. Variation of K with duty factor d and the corresponding linear fitting under three different detunings Δ of catalysis laser.
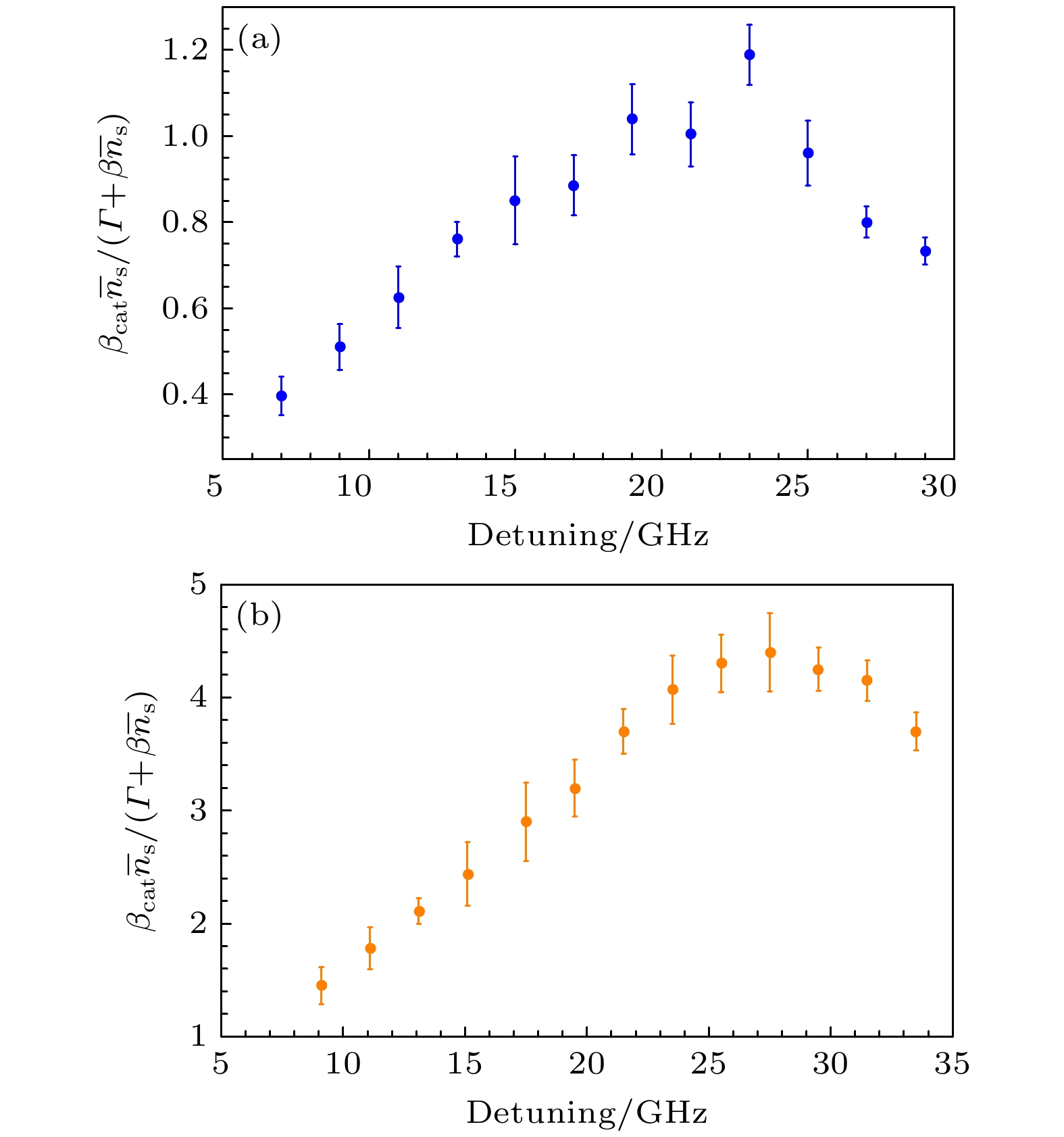
图 5 与催化激光诱导的损失率成正比的
${{\beta _{{\text{cat}}}}{{\bar n}_{\text{s}}}} / $ $ {({{{\varGamma}}_1} + \beta {{\bar n}_{\text{s}}})}$ 随催化激光失谐量Δ的变化 (a) 对应磁光阱冷却光失谐量Δ3Dc = –12 MHz, 总光功率7.36 mW/cm2; (b) 对应磁光阱冷却光失谐量Δ3Dc = –12 MHz, 总光功率20.9 mW/cm2Figure 5. Quantity
$ {{{\beta _{{\text{cat}}}}{{\bar n}_{\text{s}}}} / {({{{\varGamma}}_1} + \beta {{\bar n}_{\text{s}}})}} $ , proportional to the photoassociation induced loss rate, measured as a function of the catalysis laser detuning, Δ. The data of (a) correspond to a MOT with a cooling laser detuning of Δ3Dc = –12 MHz and a total pump laser intensity of 7.36 mW/cm2. The data of (b) correspond to a MOT with a cooling laser detuning of Δ3Dc = –12 MHz and a total pump laser intensity of 20.9 mW/cm2.
图 6 (a) 电离计测量的H2压力值Pgauge与冷原子反演真空度Patom对比图; (b) 电离计测量的N2压力值Pgauge与冷原子反演真空度Patom对比图
Figure 6. (a) Comparison of the H2 pressure measured by ionization gauge and by trapped cold atoms; (b) comparison of the N2 pressure measured by ionization gauge and by trapped cold atoms.
-
[1] Gibney E 2017 Nature 551 18
Google Scholar
[2] 范栋, 习振华, 贾文杰, 成永军, 李得天 2021 70 040602
Google Scholar
Fan D, Xi Z H, Jia W J, Cheng Y J, Li D T 2021 Acta Phys. Sin. 70 040602
Google Scholar
[3] Scherschligt J, Fedchak J A, Ahmed Z, Barker D S, Douglass K, Eckel S, Hanson E, Hendricks J, Klimov N, Purdy T, Ricker J, Singh R, Stone J 2018 J. Vac. Sci. Technol., A 36 040801
Google Scholar
[4] Calcatelli A 2013 Measurement 46 1029
Google Scholar
[5] 李得天, 成永军, 习振华 2018 宇航计测技术 38 1
Google Scholar
Li D T, Cheng Y J, Xi Z H 2018 J. Astronaut. Metrol. Meas. 38 1
Google Scholar
[6] Raab E L, Prentiss M, Cable A, Chu S, Pritchard D E 1987 Phys. Rev. Lett. 59 2631
Google Scholar
[7] Prentiss M, Cable A, Bjorkholm J E, Chu S, Raab E L 1988 Opt. Lett. 13 452
Google Scholar
[8] Bjorkholm J E 1988 Phys. Rev. A 38 1599
Google Scholar
[9] Arpornthip T, Sackett C A, Hughes K J 2012 Phys. Rev. A 85 033420
Google Scholar
[10] Yuan J P, Ji Z H, Zhao Y T, Chang X F, Xiao L T, Jia S T 2013 Appl. Opt. 52 6195
Google Scholar
[11] Xiang J F, Cheng H N, Peng X K, Wang X W, Ren W, Ji J W, Liu K K, Zhao J B, Li L, Qu Q Z, Li T, Wang B, Ye M F, Zhao X, Yao Y Y, Lü D S, Liu L 2018 Chin. Phys. B 27 073701
Google Scholar
[12] Scherschligt J, Fedchak J A, Barker D S, Eckel S, Klimov N, Makrides C, Tiesinga E 2017 Metrologia 54 125
Google Scholar
[13] Eckel S, Barker D S, Fedchak J A, Klimov N N, Norrgard E, Scherschligt J, Makrides C, Tiesinga E 2018 Metrologia 55 182
Google Scholar
[14] Barker D S, Klimov N N, Tiesinga E, Fedchak J A, Scherschligt J, Eckel S 2021 Measurement: Sensors 18 100229
[15] Makhalov V B, Martiyanov K A, Turlapov A V 2016 Metrologia 53 1287
Google Scholar
[16] Makhalov V B, Turlapov A V 2017 Quantum Electron. 47 431
Google Scholar
[17] Booth J L, Shen P R, Krems R V, Madison K W 2019 New J. Phys. 21 102001
Google Scholar
[18] Shen P R, Madison K W, Booth J L 2020 Metrologia 57 025015
Google Scholar
[19] Shen P R, Madison K W, Booth J L 2021 Metrologia 58 022101
Google Scholar
[20] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2019 Phys. Rev. A 99 042704
Google Scholar
[21] Bali S, O’Hara K M, Gehm M E, Granade S R, Thomas J E 1999 Phys. Rev. A 60 R29
Google Scholar
[22] Zhu C, Dalgarno A, Derevianko 2002 Phys. Rev. A 65 034708
Google Scholar
[23] 武跃龙, 李睿, 芮扬, 姜海峰, 武海斌 2018 67 163201
Google Scholar
Wu Y L, Li R, Rui Y, Jiang H F, Wu H B 2018 Acta Phys. Sin. 67 163201
Google Scholar
[24] Tiecke T G, Gensemer S D, Ludewig A, Walraven J T M 2009 Phys. Rev. A 80 013409
Google Scholar
[25] Hoffmann D, Bali S, Walker T 1996 Phys. Rev. A 54 1030
Google Scholar
[26] Dongen J V, Zhu C, Clement D, Dufour G, Booth J L, Madison K W 2011 Phys. Rev. A 84 022708
Google Scholar
[27] Hong S S, Shin Y H, Kim J T 2008 Measurement 41 1026
Google Scholar
[28] 李得天 2003 真空与低温 9 85
Google Scholar
Li D T 2003 Vac. Cryogenics 9 85
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5128
- PDF Downloads: 166
- Cited By: 0
