-
Λ增强型灰色黏团冷却技术(Λ gray molasses cooling, Λ- GMC)已被广泛用于制备低于亚多普勒温度极限的冷原子样品实验中. 本文设计搭建了宽范围、快速调谐的激光系统, 其调谐范围最高可达
$ 600 {\text{ MHz}} $ . 基于该激光系统, 于光学微腔中心通过铯原子D2线Λ- GMC冷却辅助腰斑大小为15 μm的交叉偶极阱中原子的装载, 相比于传统的偏振梯度冷却辅助装载, 原子数增加了约4倍, 原子温度由$ 25 {\text{ μK}} $ 降低至$ 8 {\text{ μK}} $ . 该实验对超冷原子样品实验制备和单原子阵列俘获等研究具有重要借鉴意义.Λ-enhanced gray molasses cooling (Λ-GMC) technique has been widely used in experiments to prepare cold atomic samples below the sub-Doppler temperature limit. To meet the experimental requirements of cavity quantum electrodynamics systems, we design and construct a wide-range, fast-tuning laser system by integrating tapered amplifiers, fiber phase modulators, etalon, injection locking amplification techniques etc. This laser system achieves a maximum tuning range of 600 MHz and a frequency tuning speed of 5 ns. Based on this laser system, loading atom in a crossed dipole trap assisted by cesium D2 line Λ-GMC cooling in the center of the optical microcavity is studied, and various factors affecting the atom loading are mainly as follows: laser duration$\tau $ , three-dimensional magnetic field$ \left( {{B_x}, {B_y}, {B_z}} \right) $ , single-photon detuning$\varDelta $ , two-photon detuning$\delta $ , ratio of cooling beam power to repumping beam power${I_{{\text{cool}}}}/{I_{{\text{rep}}}}$ , and cooling beam power${I_{{\text{cooling}}}}$ . The optimal parameters in this system are follows:$ \tau = 7{\text{ ms}},\; \delta = 0.2{\text{ MHz}},\; \varDelta = 5\varGamma, \;{I_{{\text{cool}}}}/{I_{{\text{rep}}}} = 3, {\text{ and }} {I_{{\text{cool}}}} = 1.2{I_{{\text{sat}}}}. $ Comparing with traditional PGC-assisted loading, the number of atoms is increased about 4 times, and the atomic temperature decreases from$ 25{\text{ μK}} $ to$ 8{\text{ μK}} $ . This experiment provides important insights for preparing ultracold atomic samples and capturing single atom arrays.-
Keywords:
- Λ-enhanced gray molasses cooling /
- Doppler temperature limit /
- wide-range frequency tuning /
- cold atom
[1] Dalibard J, Cohen-Tannoudji C 1989 J. Opt. Soc. Am. 6 2023
Google Scholar
[2] Ungar P J, Weiss D S, Riis E, Chu S 1989 J. Opt. Soc. Am. 6 2058
Google Scholar
[3] Lett P D, Phillips W D, Rolston S L, Tanner C E, Watts R N, Westbrook C I 1989 J. Opt. Soc. Am. 6 2084
Google Scholar
[4] Grynberg G, Courtois J Y 1994 EPL 27 41
Google Scholar
[5] Boiron D, Michaud A, Lemonde P, Castin Y, Salomon C, Weyers S, Szymaniec K, Cognet L, Clairon A 1996 Phys. Rev. A 53 R3734
Google Scholar
[6] Esslinger T, Sander F, Hemmerich A, Hänsch T W, Ritsch H, Weidemüller M 1996 Opt. Lett. 21 991
Google Scholar
[7] Triché C, Verkerk P, Grynberg G 1999 Eur. Phys. J. D 5 225
Google Scholar
[8] Grier A T, Ferrier-Barbut I, Rem B S, Delehaye M, Khaykovich L, Chevy F, Salomon C 2013 Phys. Rev. A 87 063411
Google Scholar
[9] Burchianti A, Valtolina G, Seman J A, Pace E, De Pas M, Inguscio M, Zaccanti M, Roati G 2014 Phys. Rev. A 90 043408
Google Scholar
[10] Sievers F, Kretzschmar N, Fernandes D R, Suchet D, Rabinovic M, Wu S, Parker C V, Khaykovich L, Salomon C, Chevy F 2015 Phys. Rev. A 91 023426
Google Scholar
[11] Colzi G, Durastante G, Fava E, Serafini S, Lamporesi G, Ferrari G 2016 Phy. Rev. A 93 023421
Google Scholar
[12] Shi Z L, Li Z L, Wang P J, Meng Z M, Huang L H, Zhang J 2018 Chin. Phys. Lett. 35 123701
Google Scholar
[13] Nath D, Easwaran R K, Rajalakshmi G, Unnikrishnan C S 2013 Phys. Rev. A 88 053407
Google Scholar
[14] Bruce G D, Haller E, Peaudecerf B, Cotta D A, Andia M, Wu S, Johnson M Y H, Lovett B W, Kuhr S 2017 J. Phys. B: At. Mol. Opt. Phys. 50 095002
Google Scholar
[15] Chen H Z, Yao, X C, Wu Y P, Liu X P, Wang X Q, Wang Y X, Pan J W 2016 Phys. Rev. A 94 033408
Google Scholar
[16] Rosi S, Burchianti A, Conclave S, Naik D S, Roati G, Fort C, Minardi F 2018 Sci. Rep. 8 1301
Google Scholar
[17] Hsiao Y F, Lin Y J, Chen Y C 2018 Phys. Rev. A 98 033419
Google Scholar
[18] Naik D S, Eneriz-Imaz H, Carey M, Freegarde T, Minardi F, Battelier B, Bouyer P, Bertoldi A 2020 Phys. Rev. Res. 2 013212
Google Scholar
[19] Liu Y X, Wang Z H, Yang P F, Wang Q X, Fan Q, Guan S J, Li G, Zhang P F, Zhang T 2023 Phys. Rev. Lett. 130 173601
Google Scholar
[20] Reiserer A, Nölleke C, Ritter S, Rempe G 2013 Phys. Rev. Lett. 110 223003
Google Scholar
[21] Hsiao Y F, Tsai P J, Chen H S, Lin S X, Hung C C, Lee C H, Chen Y, Chen Y, Yu I, Chen Y C 2018 Phys. Rev. Lett. 120 183602
Google Scholar
[22] Lounis B, Cohen-Tannoudji C 1992 J. Phys. II France 2 579
Google Scholar
[23] Tuchendler C, Lance A M, Browaeys A, Sortais Y R P, Grangier P 2008 Phys. Rev. A 78 033425
Google Scholar
[24] Brown M O, Thiele T, Kiehl C, Hsu T W, Regal C A 2019 Phys. Rev. X 9 011057
Google Scholar
[25] Huang C, Covey J P, Gadway B 2022 Phys. Rev. Res. 4 013240
Google Scholar
[26] Albrecht B, Meng Y, Clausen C, Dareau A, Schneeweiss P, Rauschenbeutel A 2016 Phys. Rev. A 94 061401
Google Scholar
[27] Schlosser N, Reymond G, Grangier P 2002 Phys. Rev. Lett. 89 023005
Google Scholar
[28] Grünzweig T, Hilliard A, McGovern M, Andersen M F 2010 Nat. Phys. 6 951
Google Scholar
-
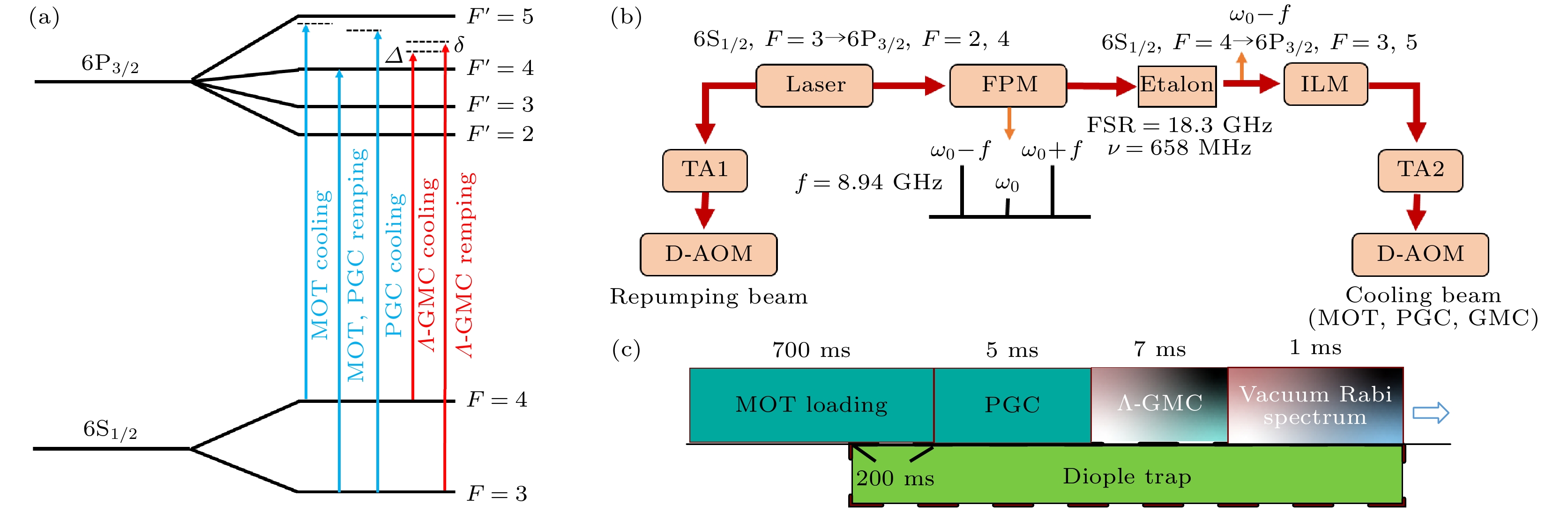
图 1 (a)铯原子 D2 线能级图; (b)快速、宽范围调谐激光系统产生过程, TA为锥型放大器, Laser为激光器, FPM为光纤位相调制器, Etalon为标准具, ILM为注入锁定放大, D-AOM为双通声光调制器; (c)时序图
Fig. 1. (a) Cesium atom D2 line energy level diagram; (b) process of generating a fast and wide-range tunable laser system, TA reprsents tapered amplifier, Laser reprsents laser source; FPM reprsents fiber phase modulator, Etalon reprsents reference cavity, ILM reprsents injection-locked amplifier, D-AOM reprsents double-acousto-optic modulators; (c) time sequence for the experiment.
图 2 (a)原子数随激光作用时间$\tau $的变化关系; (b)原子数随磁场大小的变化关系
Fig. 2. (a) The relationship between the atom number and the laser duration; (b) the relationship between the atom number and the magnitude of the magnetic field.
图 3 单光子失谐$ \varDelta $和双光子失谐$ \delta $实验优化 (a)原子数随$ \varDelta $的变化关系; (b)原子数随$ \delta $的变化关系
Fig. 3. Experimental optimization of single-photon detuning and two-photon detuning: (a) The relationship between the atom number and $ \varDelta $; (b) the relationship between the atom number and $ \delta $.
图 4 激光强度优化 (a)原子数随${I_{{\text{cool}}}}/{I_{{\text{rep}}}}$的变化关系; (b)原子数随${I_{{\text{cool}}}}$的变化关系
Fig. 4. Experimental optimization of the laser intensity: (a) The relationship between the atom number and ${I_{{\text{cool}}}}/{I_{{\text{rep}}}}$; (b) the relationship between the atom number and ${I_{{\text{cool}}}}$.
图 5 原子温度测量与评估 (a) PGC 冷却后原子温度评估; (b) PGC+Λ-GMC 组合冷却后原子温度评估
Fig. 5. Atomic temperature measurement and evaluation: (a) Evaluation of atomic temperature after PGC cooling; (b) evaluation of atomic temperature after combined cooling with PGC+Λ-GMC.
图 A1 聚焦偶极阱阱深最大(Z = 0)处横截面的虚磁场梯度图. 偶极阱激光传播方向为 Z, 偏振方向为 X
Fig. A1. The fictitious magnetic field gradient of the transverse cuts at Z = 0 inside the focused dipole trap. The propagation direction of the dipole trap laser is into the plane (along Z), and the laser is polarized along X.
图 B1 小角度 3D-MOT 装置示意图
Fig. B1. The schematic diagram of the small angle 3D-MOT set-up.
-
[1] Dalibard J, Cohen-Tannoudji C 1989 J. Opt. Soc. Am. 6 2023
Google Scholar
[2] Ungar P J, Weiss D S, Riis E, Chu S 1989 J. Opt. Soc. Am. 6 2058
Google Scholar
[3] Lett P D, Phillips W D, Rolston S L, Tanner C E, Watts R N, Westbrook C I 1989 J. Opt. Soc. Am. 6 2084
Google Scholar
[4] Grynberg G, Courtois J Y 1994 EPL 27 41
Google Scholar
[5] Boiron D, Michaud A, Lemonde P, Castin Y, Salomon C, Weyers S, Szymaniec K, Cognet L, Clairon A 1996 Phys. Rev. A 53 R3734
Google Scholar
[6] Esslinger T, Sander F, Hemmerich A, Hänsch T W, Ritsch H, Weidemüller M 1996 Opt. Lett. 21 991
Google Scholar
[7] Triché C, Verkerk P, Grynberg G 1999 Eur. Phys. J. D 5 225
Google Scholar
[8] Grier A T, Ferrier-Barbut I, Rem B S, Delehaye M, Khaykovich L, Chevy F, Salomon C 2013 Phys. Rev. A 87 063411
Google Scholar
[9] Burchianti A, Valtolina G, Seman J A, Pace E, De Pas M, Inguscio M, Zaccanti M, Roati G 2014 Phys. Rev. A 90 043408
Google Scholar
[10] Sievers F, Kretzschmar N, Fernandes D R, Suchet D, Rabinovic M, Wu S, Parker C V, Khaykovich L, Salomon C, Chevy F 2015 Phys. Rev. A 91 023426
Google Scholar
[11] Colzi G, Durastante G, Fava E, Serafini S, Lamporesi G, Ferrari G 2016 Phy. Rev. A 93 023421
Google Scholar
[12] Shi Z L, Li Z L, Wang P J, Meng Z M, Huang L H, Zhang J 2018 Chin. Phys. Lett. 35 123701
Google Scholar
[13] Nath D, Easwaran R K, Rajalakshmi G, Unnikrishnan C S 2013 Phys. Rev. A 88 053407
Google Scholar
[14] Bruce G D, Haller E, Peaudecerf B, Cotta D A, Andia M, Wu S, Johnson M Y H, Lovett B W, Kuhr S 2017 J. Phys. B: At. Mol. Opt. Phys. 50 095002
Google Scholar
[15] Chen H Z, Yao, X C, Wu Y P, Liu X P, Wang X Q, Wang Y X, Pan J W 2016 Phys. Rev. A 94 033408
Google Scholar
[16] Rosi S, Burchianti A, Conclave S, Naik D S, Roati G, Fort C, Minardi F 2018 Sci. Rep. 8 1301
Google Scholar
[17] Hsiao Y F, Lin Y J, Chen Y C 2018 Phys. Rev. A 98 033419
Google Scholar
[18] Naik D S, Eneriz-Imaz H, Carey M, Freegarde T, Minardi F, Battelier B, Bouyer P, Bertoldi A 2020 Phys. Rev. Res. 2 013212
Google Scholar
[19] Liu Y X, Wang Z H, Yang P F, Wang Q X, Fan Q, Guan S J, Li G, Zhang P F, Zhang T 2023 Phys. Rev. Lett. 130 173601
Google Scholar
[20] Reiserer A, Nölleke C, Ritter S, Rempe G 2013 Phys. Rev. Lett. 110 223003
Google Scholar
[21] Hsiao Y F, Tsai P J, Chen H S, Lin S X, Hung C C, Lee C H, Chen Y, Chen Y, Yu I, Chen Y C 2018 Phys. Rev. Lett. 120 183602
Google Scholar
[22] Lounis B, Cohen-Tannoudji C 1992 J. Phys. II France 2 579
Google Scholar
[23] Tuchendler C, Lance A M, Browaeys A, Sortais Y R P, Grangier P 2008 Phys. Rev. A 78 033425
Google Scholar
[24] Brown M O, Thiele T, Kiehl C, Hsu T W, Regal C A 2019 Phys. Rev. X 9 011057
Google Scholar
[25] Huang C, Covey J P, Gadway B 2022 Phys. Rev. Res. 4 013240
Google Scholar
[26] Albrecht B, Meng Y, Clausen C, Dareau A, Schneeweiss P, Rauschenbeutel A 2016 Phys. Rev. A 94 061401
Google Scholar
[27] Schlosser N, Reymond G, Grangier P 2002 Phys. Rev. Lett. 89 023005
Google Scholar
[28] Grünzweig T, Hilliard A, McGovern M, Andersen M F 2010 Nat. Phys. 6 951
Google Scholar
下载:
计量
- 文章访问数: 1101
- PDF下载量: 69
- 被引次数: 0
