基于DNA编码与交替量子随机行走的彩色图像加密算法

王一诺; 宋昭阳; 马玉林; 华南; 马鸿洋

doi:10.7498/aps.70.20211255

摘要

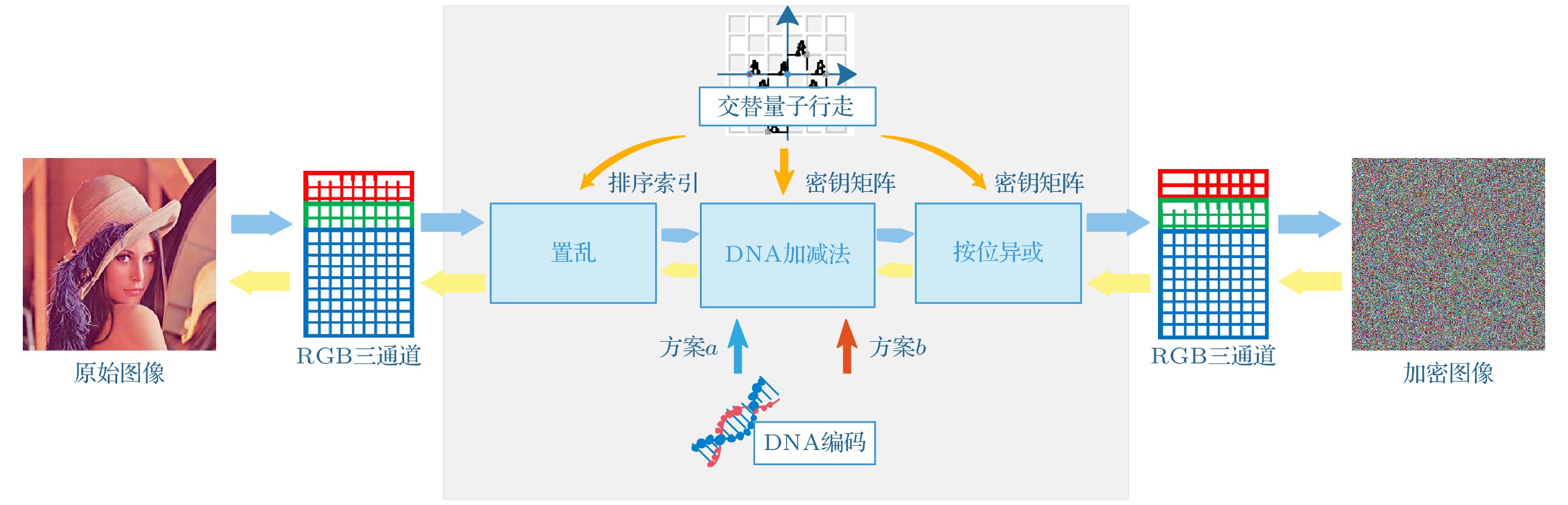
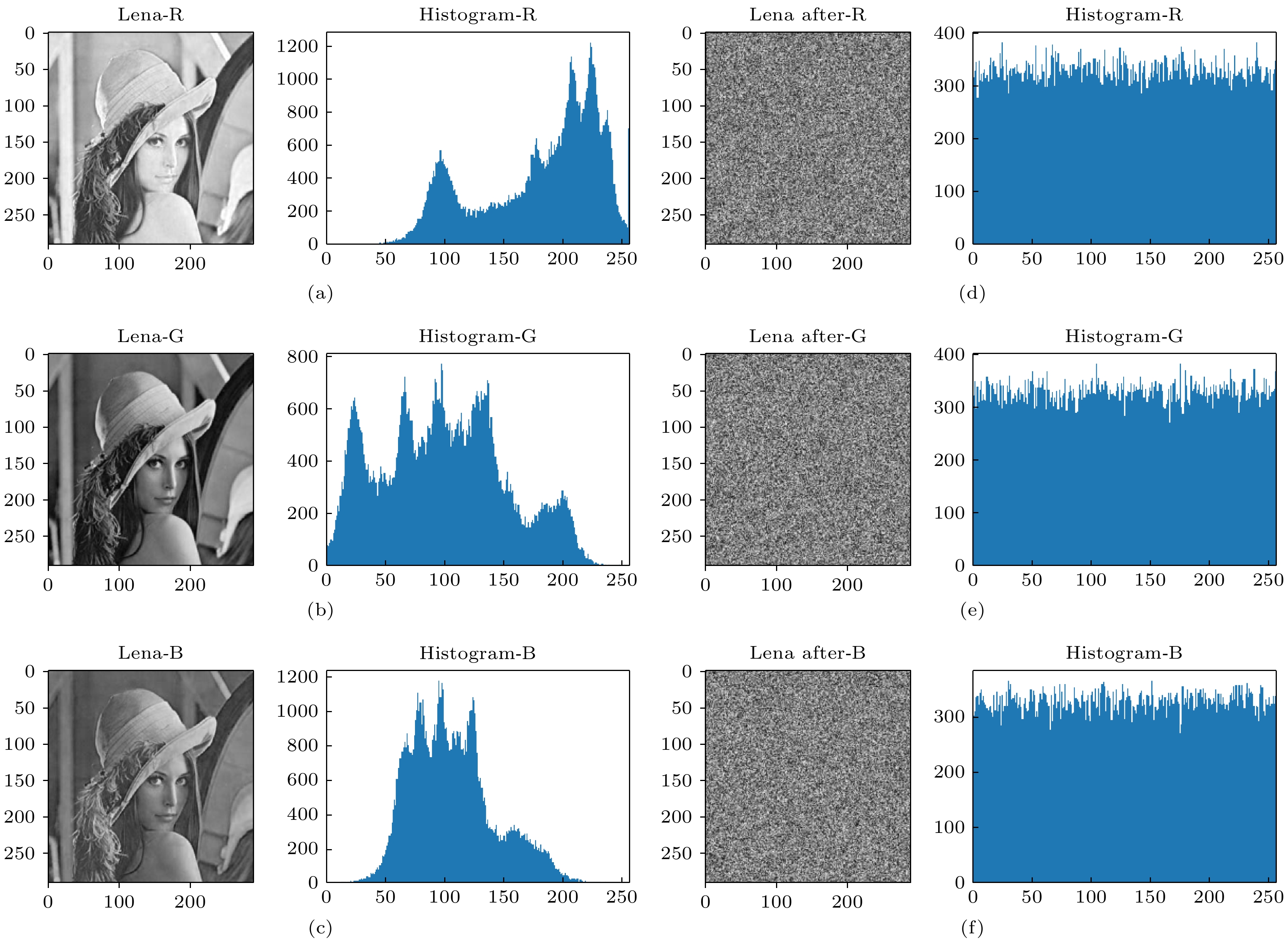
近年来, 图像加密技术备受关注. 随着人们对通信隐私及网络安全重视程度的提高, 对信息加密技术的要求更加严格, 图像作为信息的载体之一, 因携带信息的有效性和生动性而受到重视. 本文提出一种基于DNA编码与交替量子随机行走的彩色图像加密算法. 量子随机行走作为出色的密码学工具参与算法流程中各个部分, DNA编码作为核心加密方式完成算法. 本文详细描述加密、解密流程, 并对所提出算法进行仿真实验验证与结果分析. 仿真阶段设计模拟密钥参数, 编码进行彩色图像加密、解密实验, 并进行了相关分析. 实验结果表明, 本文提出的彩色图像加密算法能够进行安全有效的彩色图像加密, 且相关分析表示其加密后图像直方图平稳、像素相关性系数趋近于0、密钥空间${2^{ 128}} $, 三通道信息熵达到7.997以上, 能够抵御统计攻击、穷举攻击等攻击手段. 此外, DNA编码除新颖的编码及运算方式之外还有其独特的生物学特性, 为密码学的研究提供了新的思路与方向.

关键词:

Abstract

In recent years, image encryption technology has attracted much attention. As people pay more attention to communication privacy and network security, the requirements for information encryption technology are more stringent. As one of the information carriers, images are valuable for carrying the effectiveness and vividness of the information. This paper proposes a color image encryption algorithm based on DNA encoding and alternating quantum random walk. Quantum random walk is an excellent cryptographic tool that participates in all parts of the algorithm process, and DNA encoding is used as the core encryption method to complete the algorithm. This article describes the encryption and decryption process in detail, and conducts simulation experiments to verify and analyze the results of the proposed algorithm. In the simulation stage, we design the simulation key parameters, encode the color image encryption and decryption experiments, and carry out related analysis. The experimental results show that the color image encryption algorithm proposed in this paper can perform safe and effective color image encryption. The correlation analysis shows that the image histogram after encryption is stable, the pixel correlation coefficient approaches 0, and the key space is ${2^{ 128 }} $, the three-channel information entropy reaches more than 7.997, which can resist statistical attacks, brute force attacks and other attack methods. In addition, DNA coding has unique biological characteristics in addition to the novel coding and calculation methods, which provide new ideas and directions for cryptographic research.

Keywords:

作者及机构信息

1.
青岛理工大学理学院, 青岛　266520

2.
青岛理工大学信息与控制工程学院, 青岛　266520

通信作者: 马鸿洋, hongyang_ma@aliyun.com

基金项目: 国家自然科学基金(批准号: 11975132, 61772295)、山东省自然科学基金(批准号: ZR2019YQ01)和山东省高等教育科技计划(批准号: J18KZ012)资助的课题.

Authors and contacts

1.
School of Science, Qingdao University of Technology, Qingdao 266520, China

2.
School of Information and Control Engineering, Qingdao University of Technology, Qingdao 266520, China

Corresponding author: Ma Hong-Yang, hongyang_ma@aliyun.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11975132, 61772295), the Natural Science Foundation of Shandong Province, China (Grant No. ZR2019YQ01), and the Higher Educational Science and Technology Program of Shandong Province, China(Grant No. J18KZ012).

文章全文 : translate this paragraph

参考文献

[1]	Zheng R H, Xiao Y, Su S L, Chen Y H, Shi Z C, Song J, Xia Y, Zheng S B 2021 Phys. Rev. A 103 052402 Google Scholar
[2]	Kang Y H, Shi Z C, Huang B H, Song J, Xia Y 2020 Phys. Rev. A 101 032322 Google Scholar
[3]	Long G L 2001 Phys. Rev. A 64 022307 Google Scholar
[4]	Long G L, Li X, Sun Y 2002 Phys. Lett. A 294 143 Google Scholar
[5]	Li T, Zhang S, Fu X Q, Wang X, Wang Y, Lin J, Bao W S 2019 Chin. Phys. B 28 120301 Google Scholar
[6]	Liu F, Zhang X, Xu P A, He Z X, Ma H Y 2020 Int. J. Theor. Phys. 59 3491 Google Scholar
[7]	Zhou N R, Li J F, Yu Z B, Gong L H, A Farouk 2017 Quantum Inf. Process. 16 1 Google Scholar
[8]	Gong L H, Li J F, Zhou N R 2018 Laser Phys. Lett. 15 105204 Google Scholar
[9]	Hu X M, Huang C X, Sheng Y B, Zhou L, Liu B H, Guo Y, Zhang C, Xing W B, Huang Y F, Li C F, Guo G C 2021 Phys. Rev. Lett. 126 010503 Google Scholar
[10]	Zhou L, Sheng Y B, Long G L 2020 Sci. Bull. 65 12 Google Scholar
[11]	Yan Z H, Qin J L, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2021 Fundam. Res. 1 43 Google Scholar
[12]	Zhao J B, Zhang W B, Ma Y L, Zhang X H, Ma H Y 2020 Appl. Sci. 10 1935 Google Scholar
[13]	Qiu T H, Li H, Xie M, Liu Q, Ma H Y 2019 Opt. Express 27 27477 Google Scholar
[14]	Ma H Y, Xu P A, Shao C H, Chen L B, Li J X, Pan Q 2019 Int. J. Theor. Phys. 58 4241 Google Scholar
[15]	Li H S, Fan P, Xia H Y, Peng H L, Long G L 2020 Sci. China Phys. Mech. 63 1
[16]	Zheng R H, Kang Y H, Su S L, Song J, Xia Y 2020 Phys. Rev. A 102 012609 Google Scholar
[17]	Ma H Y, He Z X, Xu P A, Dong Y M, Fan X K 2020 Quantum Inf. Process 19 1
[18]	Xu P A, He Z X, Qiu T H, Ma H Y 2020 Opt. Express 28 12508 Google Scholar
[19]	Zhou N R, Huang L X, Gong L H, Zheng Q W 2020 Quantum Inf. Process. 19 1
[20]	Li H S, Fan P, Xia H Y, Peng H L, Long G L 2020 Sci. China. Phys. Mech. 63 1
[21]	Castagnoli G 2016 Found Phys. 46 360 Google Scholar
[22]	Castagnoli G 2016 Quanta 5 34 Google Scholar
[23]	Gong L H, Song H C, He C S, Liu Y, Zhou N R 2014 Phys. Scr. 89 035101 Google Scholar
[24]	Li H H, Gong L H, Zhou N R 2020 Chin. Phys. B 29 110304 Google Scholar
[25]	Aharonov Y, Davidovich L, Zagury N 1993 Phys. Rev. A 48 1687 Google Scholar
[26]	Farhi E, Gutmann S 1998 Phys. Rev. A 58 915 Google Scholar
[27]	Watrous J 2001 Comput. Syst. Sci. 62 376 Google Scholar
[28]	Abd El-Latif A A, Abd-El-Atty B, Venegas-Andraca S E, Elwahsh H, Piran M J, Bashir A K, Song O, Mazurczyk W 2020 IEEE Access 8 92687 Google Scholar
[29]	Abd-El-Atty B, Iliyasu A M, Alaskar H, Abd El-Latif A A 2020 Sensors 20 3108 Google Scholar
[30]	Abd EL-Latif A A, Abd-El-Atty B, Venegas-Andraca S E 2020 Physica A 547 123869 Google Scholar
[31]	Abd El-Latif A A, Abd-El-Atty B, Elseuofi S, Khalifa H S, Alghamdi A S, Polat K, Amin M 2020 Physica A 541 123687 Google Scholar
[32]	Abd-El-Atty B, Amin M, Iliyasu A M 2020 Sci. Rep. 10
[33]	Godsil C, Zhan H 2019 J. Comb. Theory Ser. A 167 181 Google Scholar
[34]	Abd-El-Atty B, Iliyasu A M, Alanezi A, Abd EL-Latif A A 2021 Opt. Lasers Eng. 138 106403 Google Scholar
[35]	Adleman L M 1994 Science 266 1021 Google Scholar
[36]	Leier A, Richter C, Banzhaf W, Rauhe H 2000 Biosystems 57 13 Google Scholar
[37]	Chen J 2003 Proceedings of the 2003 International Symposium on Circuits and Systems ISCAS'03. IEEE 2003 3 III-III.
[38]	Chang W L, Guo M, Ho M S H 2005 IEEE Trans Nanobiosci. 4 149 Google Scholar
[39]	Lu M X, Lai X J, Xiao G Z, Qin L 2007 Sci. China Inf. Sci. 50 324 Google Scholar
[40]	Lai X J, Lu M X, Qin L, Han J S, Fang X W 2010 Sci. China Inf. Sci. 53 506 Google Scholar
[41]	Wei X, Guo L, Zhang Q, Zhang J, Lian S G 2012 J. Syst. Softw. 85 290 Google Scholar
[42]	Niu Y, Zhang X, Han F 2017 Comput. Intell. Neurosci. 2017
[43]	Kalsi S, Kaur H, Chang V 2018 J. Med. Syst. 42 1 Google Scholar
[44]	Basu S, Karuppiah M, Nasipuri M, Halder A K, Radhakrishnan 2019 J. Syst. Archit. 94 24 Google Scholar
[45]	Biswas M R, Alam K M R, Tamura S, Morimoto Y 2019 J. Syst. Archit. 48 102363
[46]	Huang L, Wang S, Xiang J, Sun Y 2020 Math. Prob. Eng. 2020
[47]	Alghafis A, Firdousi F, Khan M, Batool A L, Amin M 2020 Math. Comput. Simul. 177 441 Google Scholar
[48]	Eswaran P, Shankar K 2017 Int. J. Pure Appl. Math. 118 393
[49]	Lu Q, Zhu C, Deng X 2020 IEEE Access 8 25664 Google Scholar
[50]	Wang Y, Ye S C, Wang Y 2020 Microelectron. Comput. 37 71

施引文献

图 1 双方向格点上交替量子随机行走

Fig. 1. Alternating quantum random walking on the bidirectional grid.

下载: 全尺寸图片幻灯片

图 2 算法流程图

Fig. 2. Algorithm flowchart

下载: 全尺寸图片幻灯片

图 3 加密算法仿真效果图

Fig. 3. Encryption algorithm simulation renderings.

下载: 全尺寸图片幻灯片

图 4 Lena图像加密前后相关性分析

Fig. 4. Correlation analysis of images before and after Lena encryption.

下载: 全尺寸图片幻灯片

图 6 小猫图像加密前后相关性分析

Fig. 6. Correlation analysis of images before and after cat encryption.

下载: 全尺寸图片幻灯片

图 5 蛋糕图像加密前后相关性分析

Fig. 5. Correlation analysis of images before and after cake encryption.

下载: 全尺寸图片幻灯片

图 7 Lena图像加密前后三通道直方图分析

Fig. 7. Analysis of R, G, B three-channel histogram before and after lena image encryption.

下载: 全尺寸图片幻灯片

表 1 8种DNA编码方案

Table 1. Eight DNA coding schemes.

	1	2	3	4	5	6	7	8
A	00	00	01	01	10	10	11	11
G	01	10	00	11	00	11	01	10
C	10	01	11	00	11	00	10	01
T	11	11	10	10	01	01	00	00
注: 满足DNA的生物学特性A-T互补、G-C互补.

下载: 导出CSV

表 2 DNA编码方案1对应的加法方案1

Table 2. Addition plan 1 corresponding to DNA coding plan 1.

+	A	G	C	T
A	A	G	C	T
G	G	C	T	A
C	C	T	A	G
T	T	A	G	C

下载: 导出CSV

表 3 DNA编码方案1对应的减法方案1

Table 3. DNA coding scheme 1 corresponding to subtraction scheme 1.

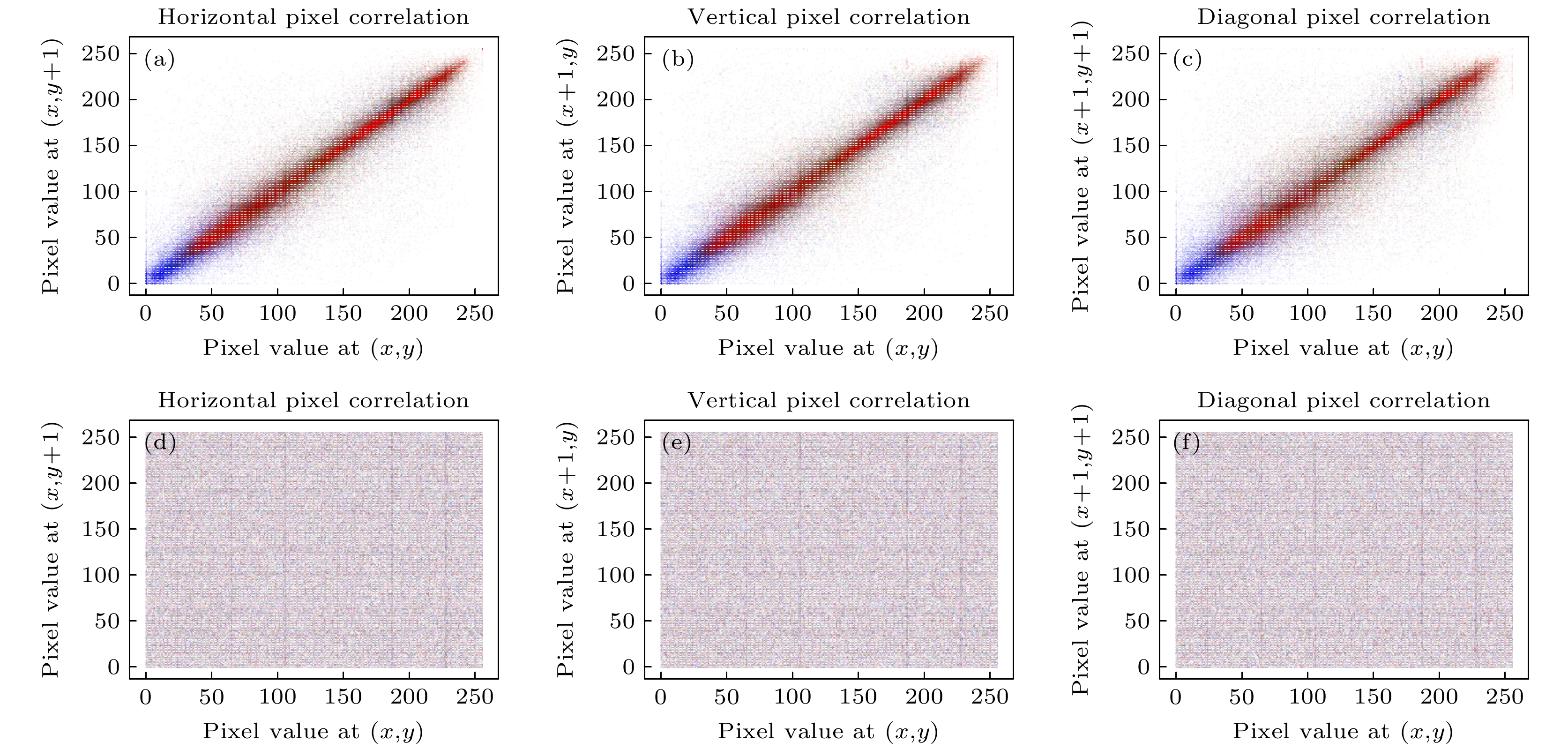
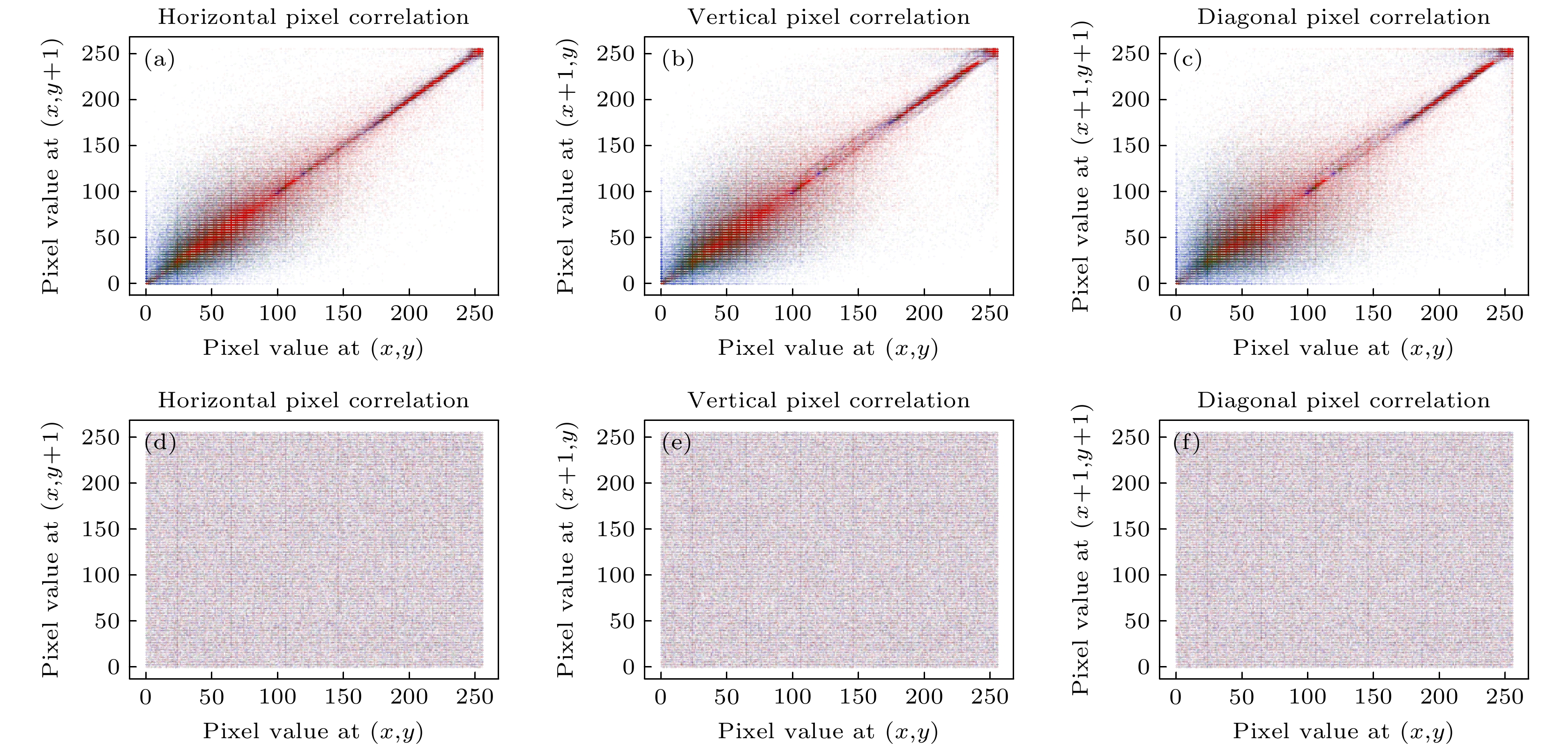
–	A	G	C	T
A	A	G	C	T
G	T	A	G	C
C	C	T	A	G
T	G	C	T	A

下载: 导出CSV

表 4 像素相关性分析数据

Table 4. Pixel correlation analysis data.

图像	方向	数值
图像	方向	原始图像	加密图像
Lena	水平	0.9275	0.0017
	垂直	0.9603	–0.0005
	对角	0.8941	0.0007
小猫	水平	0.9429	0.0026
	垂直	0.9377	0.0009
	对角	0.9097	–0.0012
蛋糕	水平	0.9229	0.0076
	垂直	0.9056	0.0017
	对角	0.8647	0.0017

下载: 导出CSV

表 5 相关性分析数据对比

Table 5. Correlation analysis data comparison.

算法	通道	平均相关性
本文	Red	水平: 0.0040
	Green	垂直: 0.0010
	Blue	对角: 0.0012
文献[42]	Red	水平: 0.0042
	Green	垂直: 0.0033
	Blue	对角: 0.0024
文献[49]	Red	水平: 0.0025
	Green	垂直: 0.0010
	Blue	对角: 0.0022
文献[50]	Red	水平: 0.0012
	Green	垂直: 0.0011
	Blue	对角: 0.0032

下载: 导出CSV

表 6 密钥敏感性分析数据

Table 6. Key sensitivity analysis data.

图像	通道	NPCR	UACI
Lena	Red	99.6040%	33.4005%
	Green	99.6195%	33.2311%
	Blue	99.5826%	33.5902%
小猫	Red	99.6326%	33.6785%
	Green	99.6124%	33.4455%
	Blue	99.6147%	33.5784%
蛋糕	Red	99.6124%	33.4461%
	Green	99.6528%	33.5315%
	Blue	99.7004%	33.4499%

下载: 导出CSV

表 7 NPCR, UACI数据对比

Table 7. Comparison of NPCR and UACI data.

算法	NPCR平均	UACI平均
本文	99.6257%	33.4835%
文献[42]	99.5506%	33.4055%
文献[49]	99.6554%	33.4675%
文献[50]	99.6150%	33.3900%

下载: 导出CSV

map

[1]	Zheng R H, Xiao Y, Su S L, Chen Y H, Shi Z C, Song J, Xia Y, Zheng S B 2021 Phys. Rev. A 103 052402 Google Scholar
[2]	Kang Y H, Shi Z C, Huang B H, Song J, Xia Y 2020 Phys. Rev. A 101 032322 Google Scholar
[3]	Long G L 2001 Phys. Rev. A 64 022307 Google Scholar
[4]	Long G L, Li X, Sun Y 2002 Phys. Lett. A 294 143 Google Scholar
[5]	Li T, Zhang S, Fu X Q, Wang X, Wang Y, Lin J, Bao W S 2019 Chin. Phys. B 28 120301 Google Scholar
[6]	Liu F, Zhang X, Xu P A, He Z X, Ma H Y 2020 Int. J. Theor. Phys. 59 3491 Google Scholar
[7]	Zhou N R, Li J F, Yu Z B, Gong L H, A Farouk 2017 Quantum Inf. Process. 16 1 Google Scholar
[8]	Gong L H, Li J F, Zhou N R 2018 Laser Phys. Lett. 15 105204 Google Scholar
[9]	Hu X M, Huang C X, Sheng Y B, Zhou L, Liu B H, Guo Y, Zhang C, Xing W B, Huang Y F, Li C F, Guo G C 2021 Phys. Rev. Lett. 126 010503 Google Scholar
[10]	Zhou L, Sheng Y B, Long G L 2020 Sci. Bull. 65 12 Google Scholar
[11]	Yan Z H, Qin J L, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2021 Fundam. Res. 1 43 Google Scholar
[12]	Zhao J B, Zhang W B, Ma Y L, Zhang X H, Ma H Y 2020 Appl. Sci. 10 1935 Google Scholar
[13]	Qiu T H, Li H, Xie M, Liu Q, Ma H Y 2019 Opt. Express 27 27477 Google Scholar
[14]	Ma H Y, Xu P A, Shao C H, Chen L B, Li J X, Pan Q 2019 Int. J. Theor. Phys. 58 4241 Google Scholar
[15]	Li H S, Fan P, Xia H Y, Peng H L, Long G L 2020 Sci. China Phys. Mech. 63 1
[16]	Zheng R H, Kang Y H, Su S L, Song J, Xia Y 2020 Phys. Rev. A 102 012609 Google Scholar
[17]	Ma H Y, He Z X, Xu P A, Dong Y M, Fan X K 2020 Quantum Inf. Process 19 1
[18]	Xu P A, He Z X, Qiu T H, Ma H Y 2020 Opt. Express 28 12508 Google Scholar
[19]	Zhou N R, Huang L X, Gong L H, Zheng Q W 2020 Quantum Inf. Process. 19 1
[20]	Li H S, Fan P, Xia H Y, Peng H L, Long G L 2020 Sci. China. Phys. Mech. 63 1
[21]	Castagnoli G 2016 Found Phys. 46 360 Google Scholar
[22]	Castagnoli G 2016 Quanta 5 34 Google Scholar
[23]	Gong L H, Song H C, He C S, Liu Y, Zhou N R 2014 Phys. Scr. 89 035101 Google Scholar
[24]	Li H H, Gong L H, Zhou N R 2020 Chin. Phys. B 29 110304 Google Scholar
[25]	Aharonov Y, Davidovich L, Zagury N 1993 Phys. Rev. A 48 1687 Google Scholar
[26]	Farhi E, Gutmann S 1998 Phys. Rev. A 58 915 Google Scholar
[27]	Watrous J 2001 Comput. Syst. Sci. 62 376 Google Scholar
[28]	Abd El-Latif A A, Abd-El-Atty B, Venegas-Andraca S E, Elwahsh H, Piran M J, Bashir A K, Song O, Mazurczyk W 2020 IEEE Access 8 92687 Google Scholar
[29]	Abd-El-Atty B, Iliyasu A M, Alaskar H, Abd El-Latif A A 2020 Sensors 20 3108 Google Scholar
[30]	Abd EL-Latif A A, Abd-El-Atty B, Venegas-Andraca S E 2020 Physica A 547 123869 Google Scholar
[31]	Abd El-Latif A A, Abd-El-Atty B, Elseuofi S, Khalifa H S, Alghamdi A S, Polat K, Amin M 2020 Physica A 541 123687 Google Scholar
[32]	Abd-El-Atty B, Amin M, Iliyasu A M 2020 Sci. Rep. 10
[33]	Godsil C, Zhan H 2019 J. Comb. Theory Ser. A 167 181 Google Scholar
[34]	Abd-El-Atty B, Iliyasu A M, Alanezi A, Abd EL-Latif A A 2021 Opt. Lasers Eng. 138 106403 Google Scholar
[35]	Adleman L M 1994 Science 266 1021 Google Scholar
[36]	Leier A, Richter C, Banzhaf W, Rauhe H 2000 Biosystems 57 13 Google Scholar
[37]	Chen J 2003 Proceedings of the 2003 International Symposium on Circuits and Systems ISCAS'03. IEEE 2003 3 III-III.
[38]	Chang W L, Guo M, Ho M S H 2005 IEEE Trans Nanobiosci. 4 149 Google Scholar
[39]	Lu M X, Lai X J, Xiao G Z, Qin L 2007 Sci. China Inf. Sci. 50 324 Google Scholar
[40]	Lai X J, Lu M X, Qin L, Han J S, Fang X W 2010 Sci. China Inf. Sci. 53 506 Google Scholar
[41]	Wei X, Guo L, Zhang Q, Zhang J, Lian S G 2012 J. Syst. Softw. 85 290 Google Scholar
[42]	Niu Y, Zhang X, Han F 2017 Comput. Intell. Neurosci. 2017
[43]	Kalsi S, Kaur H, Chang V 2018 J. Med. Syst. 42 1 Google Scholar
[44]	Basu S, Karuppiah M, Nasipuri M, Halder A K, Radhakrishnan 2019 J. Syst. Archit. 94 24 Google Scholar
[45]	Biswas M R, Alam K M R, Tamura S, Morimoto Y 2019 J. Syst. Archit. 48 102363
[46]	Huang L, Wang S, Xiang J, Sun Y 2020 Math. Prob. Eng. 2020
[47]	Alghafis A, Firdousi F, Khan M, Batool A L, Amin M 2020 Math. Comput. Simul. 177 441 Google Scholar
[48]	Eswaran P, Shankar K 2017 Int. J. Pure Appl. Math. 118 393
[49]	Lu Q, Zhu C, Deng X 2020 IEEE Access 8 25664 Google Scholar
[50]	Wang Y, Ye S C, Wang Y 2020 Microelectron. Comput. 37 71

[1]	郭牧城, 汪福东, 胡肇高, 任苗苗, 孙伟业, 肖婉婷, 刘书萍, 钟满金. 微纳尺度稀土掺杂晶体的量子相干性能及其应用研究进展. , 2023, 72(12): 120302. doi: 10.7498/aps.72.20222166
[2]	刘瀚扬, 华南, 王一诺, 梁俊卿, 马鸿洋. 基于量子随机行走和多维混沌的三维图像加密算法. , 2022, 71(17): 170303. doi: 10.7498/aps.71.20220466
[3]	方洁, 姜明浩, 安小宇, 孙军伟. 基于混沌加密和DNA编码的“一图一密”图像加密算法. , 2021, 70(7): 070501. doi: 10.7498/aps.70.20201642
[4]	李保民, 胡明亮, 范桁. 量子相干. , 2019, 68(3): 030304. doi: 10.7498/aps.68.20181779
[5]	史保森, 丁冬生, 张伟, 李恩泽. 基于拉曼协议的量子存储. , 2019, 68(3): 034203. doi: 10.7498/aps.68.20182215
[6]	窦建鹏, 李航, 庞晓玲, 张超妮, 杨天怀, 金贤敏. 量子存储研究进展. , 2019, 68(3): 030307. doi: 10.7498/aps.68.20190039
[7]	李明, 陈阳, 郭光灿, 任希锋. 表面等离激元量子信息应用研究进展. , 2017, 66(14): 144202. doi: 10.7498/aps.66.144202
[8]	李卓, 邢莉娟. 差错基、量子码与群代数. , 2013, 62(13): 130306. doi: 10.7498/aps.62.130306
[9]	王云江, 白宝明, 彭进业, 王新梅. 针对X-Z型Pauli信道的量子稀疏图码的反馈式和积译码算法. , 2011, 60(3): 030306. doi: 10.7498/aps.60.030306
[10]	邢莉娟, 李卓, 张武军. 加强的量子汉明限. , 2011, 60(5): 050304. doi: 10.7498/aps.60.050304
[11]	王云江, 白宝明, 王新梅. 量子稀疏图码的反馈式迭代译码. , 2010, 59(11): 7591-7595. doi: 10.7498/aps.59.7591
[12]	姜福仕, 赵翠兰. 量子环中量子比特的声子效应. , 2009, 58(10): 6786-6790. doi: 10.7498/aps.58.6786
[13]	尹辑文, 肖景林, 于毅夫, 王子武. 库仑势对抛物量子点量子比特消相干的影响. , 2008, 57(5): 2695-2698. doi: 10.7498/aps.57.2695
[14]	邢莉娟, 李卓, 白宝明, 王新梅. 量子卷积码的编译码方法. , 2008, 57(8): 4695-4699. doi: 10.7498/aps.57.4695
[15]	李卓, 邢莉娟. 量子Generalized Reed-Solomon码. , 2008, 57(1): 28-30. doi: 10.7498/aps.57.28
[16]	王子武, 肖景林. 抛物线性限制势量子点量子比特及其光学声子效应. , 2007, 56(2): 678-682. doi: 10.7498/aps.56.678
[17]	李卓, 邢莉娟. 一类基于级联结构的量子好码. , 2007, 56(10): 5602-5606. doi: 10.7498/aps.56.5602
[18]	张权, 张尔扬. 非对称二状态量子密钥分配协议最优参量研究. , 2002, 51(8): 1684-1689. doi: 10.7498/aps.51.1684
[19]	张权, 唐朝京, 张森强. B92量子密钥分配协议的变形及其无条件安全性证明. , 2002, 51(7): 1439-1447. doi: 10.7498/aps.51.1439
[20]	张权, 唐朝京, 高峰. 量子Turbo码. , 2002, 51(1): 15-20. doi: 10.7498/aps.51.15

计量

文章访问数: 6908
PDF下载量: 241
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板